|
 |
- Search
| J. Korean Soc. Hazard Mitig. > Volume 16(1); 2016 > Article |
Abstract
This paper analyzed the reinforcement effect of concrete beam-to-column joints bonded with steel plate in reinforced concrete structures using finite element program. The limit load, ductility, and cracks of unreinforced model and reinforced model by steel plates were evaluated based on the analytical variations of reinforced steel plate area and thickness. As a result of analytical study, the maximum load of reinforced model by steel plate has 63% to 97.5% against unreinforced model. Also, to increase steel plate thickness has better performance than when steel plate area increases.
ņÜöņ¦Ć
ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö ņ£ĀĒĢ£ņÜöņåīĒĢ┤ņäØ ĒöäļĪ£ĻĘĖļשņØĖ ABAQUSļź╝ ĒåĄĒĢśņŚ¼ ņ▓ĀĻĘ╝ņĮśĒü¼ļ”¼ĒŖĖ ĻĄ¼ņĪ░ļ¼╝ ļ│┤-ĻĖ░ļæź ņĀæĒĢ®ļČĆņØś Ļ░ĢĒīÉļ│┤Ļ░ĢĒÜ©Ļ│╝ļź╝ ĒÅēĻ░ĆĒĢśņśĆļŗż. ĒĢ┤ņäØļ│ĆņłśļĪ£ļŖö Ļ░ĢĒīÉņØś ļ│┤Ļ░Ģļ®┤ņĀüĻ│╝ ļ│┤Ļ░ĢĻ░ĢĒīÉņØś ļæÉĻ╗śļź╝ ļæÉņ¢┤ ĒĢ┤ņäØņŚ░ĻĄ¼ļź╝ ņłśĒ¢ēĒĢśņśĆļŗż. ĒĢ┤ņäØĻ▓░Ļ│╝ Ļ░ĢĒīÉļ│┤Ļ░Ģ ņŗ£ ņĄ£ļīĆ ĒĢśņżæņØĆ ņĢĮ 63~97.5% ņ”ØĻ░ĆĒĢśņśĆĻ│Ā, ļé┤ņ¦äņä▒ļŖźļÅä Ēü¼Ļ▓ī Ē¢źņāüļÉśņŚłļŗż. ļśÉĒĢ£ ļ│┤Ļ░ĢĻ░ĢĒīÉņØś ļ®┤ņĀüņØä ņ”ØĻ░Ć ņŗ£ĒéżļŖö Ļ▓āļ│┤ļŗż ļæÉĻ╗śļź╝ ņ”ØĻ░Ć ņŗ£ņ╝░ņØä ļĢī ļé┤ļĀźņØ┤ Ēü¼Ļ▓ī ņ”Øņ¦äļÉśņŚłļŗż.
Ļ▒┤ņČĢĻĄ¼ņĪ░ļ¼╝ņØĆ ņŗ£Ļ░äņØ┤ Ļ▓ĮĻ│╝ĒĢ©ņŚÉ ļö░ļØ╝ ņŚ┤ĒÖöņÖĆ Ēö╝ļĪ£ĒĢśņżæ, Ēü¼Ļ│Ā ņ×æņØĆ ĻĘĀņŚ┤ ļō▒ņŚÉ ņØśĒĢśņŚ¼ ļČĆņ×¼ņØś ļŗ©ļ®┤ ņåÉņŗżņØ┤ ļ░£ņāØĒĢśļ®░, ņØ┤ļĪ£ ņØĖĒĢśņŚ¼ ĻĄ¼ņĪ░ļ¼╝ņØś Ļ░ĢļÅäņÖĆ ļé┤ļĀźņØ┤ ņĀĆĒĢśļÉ£ļŗż. ļé┤ļĀźņØ┤ ņĀĆĒĢśļÉ£ ĻĄ¼ņĪ░ļ¼╝ņØĆ ņ¦Ćņ¦ä ļ░£ņāØ ņŗ£ Ēü░ ņåÉņāüņØ┤ ņāØĻĖĖ ņłś ņ׳ļŗż. ņĄ£ĻĘ╝ ļ¬ć ļģä Ļ░ä ļ░£ņāØĒ¢łļŹś ņżæĻĄŁ ņō░ņ┤©ņä▒ ļīĆņ¦Ćņ¦ä(ņ¦äļÅä 8.0), ņ╣ĀļĀł ļīĆņ¦Ćņ¦ä(ņ¦äļÅä 8.8), ļÅÖņØ╝ļ│Ė ļīĆņ¦Ćņ¦ä(ņ¦äļÅä 9.0) ļō▒ņ£╝ļĪ£ ņŚ┤ĒÖöĻ░Ć ņ¦äĒ¢ēļÉ£ Ļ▒┤ņČĢļ¼╝ļōżņØś ĒīīĻ┤┤ļ¬©ļō£ļź╝ ņé┤ĒÄ┤ļ│┤ļ®┤ ļīĆļČĆļČä ļ©╝ņĀĆ ļ│┤-ĻĖ░ļæź ņĀæĒĢ®ļČĆņŚÉņä£ ĒīīĻ┤┤Ļ░Ć ļéśĒāĆļé¼Ļ│Ā, ņØ┤ļĪ£ ņØĖĒĢ£ Ļ▒┤ņČĢĻĄ¼ņĪ░ļ¼╝ņØś ļé┤ļĀźņĀĆĒĢśļĪ£ Ļ▒┤ļ¼╝ņØ┤ ļČĢĻ┤┤ļÉśņŚłļŗż.
ņĄ£ĻĘ╝ ĻĄŁļé┤┬ĘņÖĖņŚÉņä£ļŖö ĻĖ░ņĪ┤ Ļ▒┤ņČĢļ¼╝ņØś ļ│┤ņłś┬Ęļ│┤Ļ░ĢņŚÉ ļīĆĒĢ£ Ļ┤Ćņŗ¼Ļ│╝ ĒĢäņÜöņä▒ņØ┤ Ļ│ĀņĪ░ļÉ©ņŚÉ ļö░ļØ╝ ļ¦ÄņØĆ ļ│┤ņłś┬Ęļ│┤Ļ░Ģ Ļ│Ąļ▓ĢņØ┤ Ļ░£ļ░£ļÉśņŚłĻ│Ā ļ│┤Ļ░Ģ Ļ│Ąļ▓ĢņŚÉ ļīĆĒĢ£ ņŚ░ĻĄ¼ļÅä ĒÖ£ļ░£Ē׳ ņ¦äĒ¢ēļÉśĻ│Ā ņ׳ļŗż. Hong et al. (2005)ņØĆ ņ▓ĀĻĘ╝ņĮśĒü¼ļ”¼ĒŖĖ ļ│┤-ĻĖ░ļæź ņĀæĒĢ®ļČĆņØś ļŗżņ¢æĒĢ£ ļ│┤ņłś ļ░Å ļ│┤Ļ░ĢĻ│Ąļ▓ĢņŚÉ ļīĆĒĢ£ ļ╣äĻĄÉņŚ░ĻĄ¼ļź╝ ņŗżņŗ£ĒĢ£ Ļ▓░Ļ│╝, Ļ░ĢĒīÉļ│┤Ļ░ĢĻ│Ąļ▓ĢņØ┤ ļŗżļźĖ Ļ│Ąļ▓ĢņŚÉ ļ╣äĒĢ┤ ļ╣äĻĄÉņĀü ņŗ£Ļ│ĄņØ┤ ņēĮĻ│Ā ņÜ░ņłśĒĢ£ ļé┤ņ¦äņä▒ļŖźņØä ļ│┤ņ£ĀĒĢ£ Ļ▓āņ£╝ļĪ£ ļéśĒāĆļé┤ņŚłļŗż.
Ļ░ĢĒīÉļ│┤Ļ░ĢĻ│Ąļ▓ĢņŚÉ ļīĆĒĢ£ ņŗżņĀ£ ņŗ£Ļ│Ą ņé¼ļĪĆļŖö Ļ▒┤ņČĢļ¼╝ņØś ļ│┤ņłś┬Ęļ│┤Ļ░ĢņØä ņĀäļ¼ĖņĀüņ£╝ļĪ£ ņłśĒ¢ēĒĢśļŖö ņŚģņ▓┤ņŚÉ ĻĄŁĒĢ£ļÉśņ¢┤ ņ׳ņ£╝ļ®░, ĒĢÖĻ│äņŚÉņä£ļŖö ņØ┤ņŚÉ Ļ┤ĆļĀ©ĒĢ£ ņŚ░ĻĄ¼ ņé¼ļĪĆļŖö ļ»Ėļ╣äĒĢ£ ņŗżņĀĢņØ┤ļŗż. ļö░ļØ╝ņä£ ļ│Ė ņŚ░ĻĄ¼ ņłśĒ¢ēņØä ĒåĄĒĢ┤ Ļ░ĢĒīÉļ│┤Ļ░ĢĻ│Ąļ▓ĢņŚÉ ļīĆĒĢ£ ĒĢ®ļ”¼ņĀüņØ┤Ļ│Ā ņ▓┤Ļ│äņĀüņØĖ ļ│┤ņłśļ│┤Ļ░Ģ ņäżĻ│äļ▓ĢņØä Ļ░£ļ░£ĒĢśĻĖ░ ņ£äĒĢ£ ĻĖ░ņ┤łņ×ÉļŻīļĪ£ ņĀ£Ļ│ĄĒĢśĻ│Āņ×É ĒĢ£ļŗż.
ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö ņ▓ĀĻĘ╝ņĮśĒü¼ļ”¼ĒŖĖ ĻĄ¼ņĪ░ļ¼╝ņØś ļ│┤-ĻĖ░ļæź ņĀæĒĢ®ļČĆņŚÉ Ļ░ĢĒīÉņØä ļ│┤Ļ░ĢĒĢ©ņ£╝ļĪ£ņŹ© ņØ┤ņŚÉ ļīĆĒĢ£ ĻĄ¼ņĪ░ņä▒ļŖźņØä ņ£ĀĒĢ£ņÜöņåīĒĢ┤ņäØ ĒöäļĪ£ĻĘĖļשņØĖ ABAQUSļź╝ ņØ┤ņÜ®ĒĢśņŚ¼ ĒÅēĻ░ĆĒĢśņśĆļŗż. ļ│ĆņłśļĪ£ļŖö Ļ░ĢĒīÉ ļ│┤Ļ░Ģ ņ£äņ╣ś, Ļ░ĢĒīÉņØś ļŗ©ļ®┤Ļ│╝ ļæÉĻ╗śļź╝ ļ│ĆņłśļĪ£ ļæÉņ¢┤ ņ£ĀĒĢ£ņÜöņåīĒĢ┤ņäØ ņŚ░ĻĄ¼ļź╝ ņłśĒ¢ēĒĢśņśĆļŗż.
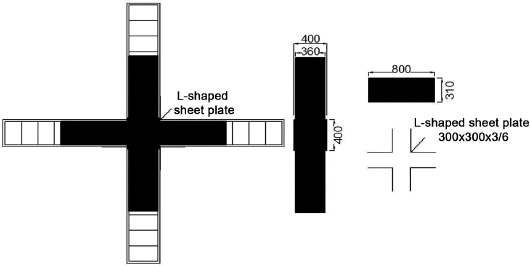
ņ▓ĀĻĘ╝ņĮśĒü¼ļ”¼ĒŖĖĻĄ¼ņĪ░ļ¼╝ņØś ļ│┤-ĻĖ░ļæź ņĀæĒĢ®ļČĆņŚÉņä£ ĒĢśņżæ ņĀäļŗ¼ ļ®öņ╗żļŗłņ”śņØä Fig. 1ņŚÉ ļéśĒāĆļé┤ņŚłļŗż. ļ│┤-ĻĖ░ļæź ņĀæĒĢ®ļČĆņŚÉņä£ ļ│┤ņØś ļŗ©ļČĆņÖĆ ĻĖ░ļæźņØś ļŗ©ļČĆļŖö ĻĄ¼ņĪ░ļ¼╝ņØś ļé┤ļĀźņØä ņĀäļŗ¼ĒĢśļŖö ņżæņÜöĒĢ£ ļČĆļČäņØ┤ļŗż. ļ│┤-ĻĖ░ļæź ņĀæĒĢ®ļČĆĻ░Ć ĒīīĻ┤┤ļÉśļ®┤ ĻĄ¼ņĪ░ļ¼╝ņØś ļČĢĻ┤┤ļĪ£ ņØ┤ņ¢┤ņ¦ł ņłś ņ׳ļŗż. ļśÉĒĢ£ ļ│┤-ĻĖ░ļæź ņĀæĒĢ®ļČĆņŚÉņä£ ļ│┤ ļŗ©ļČĆļéś ĻĖ░ļæź ļŗ©ļČĆņŚÉņä£ ņ×æņÜ®ļÉ£ Ē£©ļ¬©ļ®śĒŖĖ(Mb, Mh)ņÖĖņŚÉ ņČöĻ░ĆņĀüņ£╝ļĪ£ ņ▓ĀĻĘ╝ņØ┤ ļ░øļŖö ņØĖņןļĀź(Ts)Ļ│╝ ņĢĢņČĢļĀź(Cs)ņŚÉ ņØśĒĢ£ ņÜ░ļĀźļ¬©ļ®śĒŖĖĻ░Ć ļ░£ņāØĒĢĀ ņłś ņ׳ļŗż. ļ│┤-ĻĖ░ļæź ņĀæĒĢ®ļČĆņŚÉņä£ ņØĖņןļĀźņØĆ ņ▓ĀĻĘ╝ņØś ļČĆņ░® ņØæļĀźņØä ĒåĄĒĢśņŚ¼ ņĀæĒĢ®ļČĆņŚÉ ņĀäļŗ¼ļÉ£ļŗż. ļö░ļØ╝ņä£ ļ│┤-ĻĖ░ļæź ņĀæĒĢ®ļČĆņØś ļīĆĻ░üņäĀļ░®Ē¢źņ£╝ļĪ£ ņĢĢņČĢņØæļĀźĻ│╝ ņØĖņןņØæļĀźņØ┤ ĒśĢņä▒ļÉ£ļŗż. ļö░ļØ╝ņä£ ņ▓ĀĻĘ╝ņĮśĒü¼ļ”¼ĒŖĖ ĻĄ¼ņĪ░ļ¼╝ņØ┤ ļ░śļ│ĄĒĢśņżæņØä ļ░øņØä Ļ▓ĮņÜ░ ļ│┤-ĻĖ░ļæź ņĀæĒĢ®ļČĆņŚÉņä£ ņé¼ņØĖņן ĻĘĀņŚ┤ņØ┤ ļ░£ņāØĒĢśņŚ¼ ņØ┤ņŚÉ ļīĆĒĢ£ ļ│┤Ļ░ĢņØ┤ ĒĢäņÜöĒĢśļŗż.
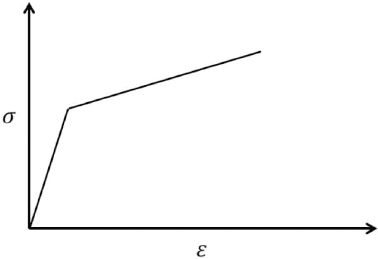
ņ¦ĆĻĖłĻ╣īņ¦Ć ĻĄŁļé┤┬ĘņÖĖ ņŚ░ĻĄ¼ņ×ÉļōżņØĆ ņĮśĒü¼ļ”¼ĒŖĖ ĻĄ¼ņĪ░ļ¬©ļŹĖņØä ņé¼ņÜ®ĒĢĀ ļĢī Kent-Park ĻĄ¼ņĪ░ļ¬©ļŹĖņØä ļ¦ÄņØ┤ ņäĀĒāØĒĢśņśĆļŗż. Kent-Park ĻĄ¼ņĪ░ļ¬©ļŹĖņØś Ēæ£ņżĆ ņØæļĀź-ļ│ĆĒśĢļÅäļź╝ Fig. 2ņŚÉ ļéśĒāĆļé┤ņŚłļŗż. Fig. 2ņŚÉņä£ ╬ĄcoņĀÉņØĆ ņĮśĒü¼ļ”¼ĒŖĖņØś ņĄ£ļīĆĒĢ£Ļ│äņāüĒā£ņØ┤Ļ│Ā, Z ┬Ę K ┬Ę fcŌĆÖ ĻĄ¼Ļ░äņŚÉņä£ ņ┤łĻĖ░ ĻĘĀņŚ┤ņØ┤ ļéśĒāĆļé£ļŗż. ╬Ąc1ņĀÉņØĆ ņĮśĒü¼ļ”¼ĒŖĖņØś ņĀäļŗ©ļ®┤ņŚÉņä£ ņÖäņĀäĒ׳ ĒīīĻ┤┤ļÉ£ ņāüĒā£ņØ┤ļŗż. ņØ┤ ĻĘĖļלĒöäļź╝ ĒåĀļīĆļĪ£ ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö ņĮśĒü¼ļ”¼ĒŖĖ ļ¬©ļŹĖņŚÉ ņ▓ĀĻĘ╝ ĻĄ¼ņåŹņØä Ļ│ĀļĀżĒĢśņ¦Ć ņĢŖņĢśļŗż. ļö░ļØ╝ņä£ ļģĖĒøäĒÖö ļÉ£ ņĮśĒü¼ļ”¼ĒŖĖņØś ņØĖņןĻ░ĢļÅäņÖĆ ņĢĢņČĢĻ░ĢļÅäļź╝ Ļ░üĻ░ü ņ×ģļĀźĒĢśņŚ¼ ņĀüņÜ®ĒĢśņśĆļŗż. ļśÉĒĢ£, ļ│Ė ĒĢ┤ņäØņŚ░ĻĄ¼ņŚÉņä£ ņé¼ņÜ®ļÉ£ ņ▓ĀĻĘ╝Ļ│╝ Ļ░ĢĒīÉņØś ĻĄ¼ņĪ░ļ¬©ļŹĖņØĆ Fig. 3ņŚÉņä£ ļéśĒāĆļé┤ņŚłļŗż. ņ▓ĀĻĘ╝Ļ│╝ Ļ░ĢĒīÉņØĆ ņ▓ĀĻĘ╝Ēü░Ēü¼ļ”¼ĒŖĖ ļ¬©ļŹĖņŚÉ ļ╣äĒĢśņŚ¼ ņ×¼ļŻīņØś ņŚŁĒĢÖņĀü Ļ┤ĆĻ│äĻ░Ć ļŗ©ņł£ĒĢśļ»ĆļĪ£ Elastoplasticity Modelļź╝ ņé¼ņÜ®ĒĢśņśĆļŗż.
ņ£ĀĒĢ£ņÜöņåīĒĢ┤ņäØ ĒöäļĪ£ĻĘĖļשņØĖ ABAQUSņŚÉņä£ ņĮśĒü¼ļ”¼ĒŖĖ ļ¬©ļŹĖļ¦üņŗ£ ņĮśĒü¼ļ”¼ĒŖĖņØś ĒīīĻ┤┤Ļ│äņłśļź╝ Ļ│ĀļĀżĒĢśņŚ¼ņĢ╝ ĒĢ£ļŗż. ĒīīĻ┤┤Ļ│äņłśļŖö ņ┤łĻĖ░ Ēāäņä▒Ļ│äņłśļź╝ ļéśĒāĆļé┤Ļ│Ā ņĢĢņČĢĒīīĻ┤┤Ļ│äņłśņÖĆ ņØĖņןĒīīĻ┤┤Ļ│äņłśĻ░Ć ņ׳ļŗż. ņØ┤ Ļ│äņłśļŖö ņĮśĒü¼ļ”¼ĒŖĖ ņåīņä▒ ņāüĒā£ņØś ņĀĢļÅäļź╝ Ļ▓░ņĀĢĒĢĀ ņłś ņ׳ļŗż. ņĮśĒü¼ļ”¼ĒŖĖņØś ĒīīĻ┤┤Ļ│äņłś ņØ┤ņÖĖņŚÉļÅä ņĮśĒü¼ļ”¼ĒŖĖņØś ņĢĢņČĢļĀźĻ│╝ ņØĖņןļĀźņØä ļ░øņĢä ņāØĻĖ░ļŖö ņåīņä▒ļ│ĆĒśĢĻ│╝ Ēāäņä▒ļ│ĆĒśĢņØä ļ¬©ļæÉ Ļ│ĀļĀżĒĢśņŚ¼ ļ¬©ļŹĖļ¦üņŚÉ ņĀüņÜ®ĒĢśņŚ¼ņĢ╝ ĒĢ£ļŗż.
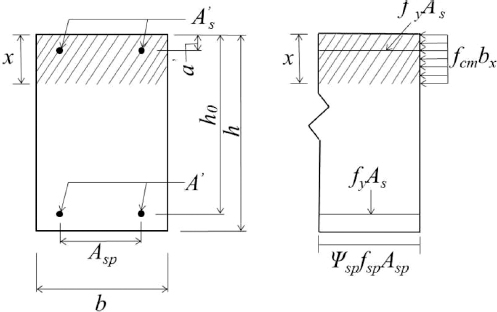
ļ│┤Ļ░ĢĻ░ĢĒīÉņØś Ēü¼ĻĖ░ņÖĆ ņ£äņ╣śļź╝ Ļ▓░ņĀĢĒĢśĻĖ░ ņ£äĒĢ┤ņä£ļŖö ļ│┤Ļ░Ģ ņĀä ņĮśĒü¼ļ”¼ĒŖĖņØś Ļ░ĢļÅäņÖĆ ņĢĢņČĢļČĆ ĻĖĖņØ┤ļź╝ ņé░ņĀĢĒĢśņŚ¼ņĢ╝ ņäżĻ│äĻ░Ć ņØ┤ļŻ©ņ¢┤ņĀĖņĢ╝ ĒĢ£ļŗż. ļ│┤Ļ░ĢĻ░ĢĒīÉņØś ņäżĻ│äņŚÉ Ļ┤ĆĒĢ£ ņāüĻ┤Ć Ļ│äņé░ņŗØņØä ņŗØ(1) ~ ņŗØ(6)ņŚÉ ļéśĒāĆļé┤ņŚłļŗż. ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö Fig. 4ņŚÉ ļéśĒāĆļéĖ ļ░öņÖĆ Ļ░ÖņØ┤ ņé¼ņÜ®ĒĢ£ ņĮśĒü¼ļ”¼ĒŖĖ ļ│┤ņØś ĒÅŁņØä b, Ļ╣ŖņØ┤ļź╝ hļĪ£ ļéśĒāĆļé┤ņŚłļŗż.
ļ│┤Ļ░Ģ ņĀä ņĮśĒü¼ļ”¼ĒŖĖņØś ņĢĢņČĢļČĆ ĻĖĖņØ┤, x (mm):
ļ│┤Ļ░Ģ ņĀä ņĮśĒü¼ļ”¼ĒŖĖņØś Ē£©ļ¬©ļ®śĒŖĖ, Mmax (kN┬Ęm):
ļ│┤Ļ░Ģ Ēøä ņĮśĒü¼ļ”¼ĒŖĖņØś ņĢĢņČĢ ļČĆļČäņØś ĻĖĖņØ┤, xs (mm):
ļ│┤Ļ░ĢĻ░ĢĒīÉņØś ņĄ£ņåīļŗ©ļ®┤ņĀü, Asp (mm2)ļŖö:
ļ│┤Ļ░ĢĻ░ĢĒīÉ ļåÆņØ┤, B (mm) :
ļ│┤Ļ░ĢĻ░ĢĒīÉ ņĀäļŗ©ņ£äņ╣ś, Lsp (mm):
ņŚ¼ĻĖ░ņä£, As: ņØĖņןņĖĪ ņ▓ĀĻĘ╝ ļŗ©ļ®┤ņĀü (mm2), Lsp: Ļ░ĢĒīÉņØś ļ│┤Ļ░Ģ ĻĖĖņØ┤ (mm), fcm: ņĮśĒü¼ļ”¼ĒŖĖņØś ĒĢŁļ│ĄĻ░ĢļÅä (N/mm2), fbd: ĻĄ¼ņĪ░ņÜ® ņĀæņ░®ņĀ£ ņØś Ļ░ĢļÅä (N/mm2), fy: ņ▓ĀĻĘ╝ņØś ĒĢŁļ│ĄĻ░ĢļÅä (N/mm2), t: ļ│┤Ļ░Ģ Ļ░ĢĒīÉ ņØś ļæÉĻ╗ś (mm)ņØä ļéśĒāĆļéĖļŗż.
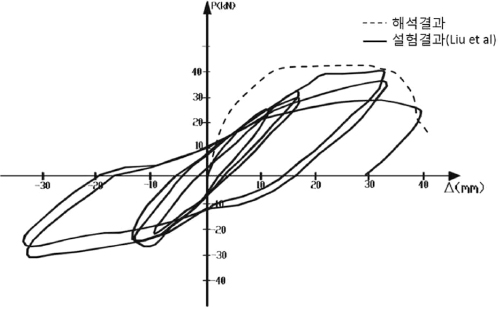
Liu et al. (2003)ņØĆ ļ░śļ│ĄĒĢśņżæņØä ļ░øļŖö ļ╣äļ│┤Ļ░Ģ ņ▓ĀĻĘ╝ņĮśĒü¼ļ”¼ĒŖĖ ļ│┤-ĻĖ░ļæź ņĀæĒĢ®ļČĆ Ļ▒░ļÅÖņŚÉ Ļ┤ĆĒĢ£ ņŗżĒŚśņŚ░ĻĄ¼ļź╝ ņłśĒ¢ēĒĢśņśĆļŗż. ņŗżĒŚśĻ▓░Ļ│╝ļź╝ ņé┤ĒÄ┤ļ│┤ļ®┤ ļ╣äļ│┤Ļ░Ģ ņŗżĒŚśņ▓┤ņØś ņóģĻĄŁņāüĒā£ņŚÉņä£ ņĮśĒü¼ļ”¼ĒŖĖņŚÉ ļéśĒāĆļé£ ļ¬©ļōĀ ĻĘĀņŚ┤ņØĆ ņŻ╝ļĪ£ ņĀæĒĢ®ļČĆņØś ļ│┤ ļŗ©ļČĆņÖĆ ļ│┤-ĻĖ░ļæź ņĀæĒĢ®ļČĆņŚÉ ņ¦æņżæļÉśņ¢┤ ļéśĒāĆļé¼ļŗż. ļö░ļØ╝ņä£ ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö ļ│┤-ĻĖ░ļæź ņĀæĒĢ®ļČĆņŚÉ ņØæļĀźņ¦æņżæĻ│╝ ļ¦ÄņØĆ ĻĘĀņŚ┤ņØ┤ ļéśĒāĆļé£ Liu et al. (2003) ņŗżĒŚśņŚ░ĻĄ¼ņØś ļ╣äļ│┤Ļ░Ģ ņŗżĒŚśņ▓┤ļź╝ ņ£ĀĒĢ£ņÜöņåīĒĢ┤ņäØ ļ¬©ļŹĖļĪ£ ņäĀņĀĢĒĢśņŚ¼ ĒĢ┤ņäØņŚ░ĻĄ¼ļź╝ ņłśĒ¢ēĒĢśņśĆļŗż. Fig. 5ņŚÉ ļéśĒāĆļéĖ ļ░öņÖĆ Ļ░ÖņØ┤, ņĀæĒĢ®ļČĆņŚÉņä£ņØś ĻĘĀņŚ┤ ļ░Å ņØæļĀźņ¦æņżæņØ┤ ņŗżļ¼╝ļīĆ ņŗżĒŚśĻ▓░Ļ│╝ņÖĆ ņ£ĀĒĢ£ņÜöņåīĒĢ┤ņäØĻ▓░Ļ│╝Ļ░Ć ņ£Āņé¼ĒĢ£ Ļ▓āņ£╝ļĪ£ ļéśĒāĆļé¼Ļ│Ā, Fig. 6ņŚÉņä£ ļ│┤ļŖö ļ░öņÖĆ Ļ░ÖņØ┤ ļŗ©ņĪ░Ļ░ĆļĀźņØä ņŗżņŗ£ĒĢ£ ĒĢ┤ņäØĻ▓░Ļ│╝Ļ░Ć ņŗżĒŚśĻ▓░Ļ│╝ņÖĆ Ļ▒░ņØś ņ£Āņé¼ĒĢ£ Ļ▓āņ£╝ļĪ£ ļéśĒāĆļé¼ļŗż.
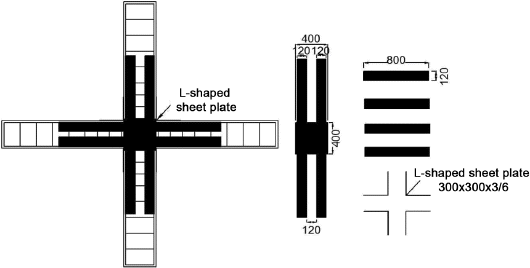
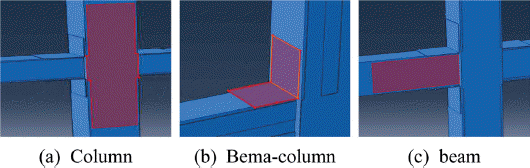
ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö ļ╣äļ│┤Ļ░Ģ ņ▓ĀĻĘ╝ņĮśĒü¼ļ”¼ĒŖĖ ļ│┤-ĻĖ░ļæź ļ¬©ļŹĖ 1Ļ░£ņÖĆ SS400Ļ░Ģņ×¼ļĪ£ ļ│┤Ļ░ĢļÉ£ ņ▓ĀĻĘ╝ņĮśĒü¼ļ”¼ĒŖĖ ļ│┤-ĻĖ░ļæź ļ¬©ļŹĖ 4Ļ░£ņŚÉ ļīĆĒĢśņŚ¼ ĒĢ┤ņäØņØä ņłśĒ¢ēĒĢśņśĆļŗż. ņ£ĀĒĢ£ņÜöņåīĒĢ┤ņäØļ¬©ļŹĖņØś ņĀ£ņøÉņØĆ Table 1Ļ│╝ Ļ░Öļŗż. ņØ╝ļ░śņĀüņ£╝ļĪ£ ļ¦ÄņØ┤ ņō░ņØ┤ļŖö ņŗżļ¼╝ļīĆ Ēü¼ĻĖ░ļĪ£ ĻĄ¼ņä▒ĒĢśņŚ¼ ĻĖ░ļæźņØś ļåÆņØ┤ļŖö 3,350 mm, ļ│┤ņØś ņŖżĒī¼ņØĆ 1,500 mmļĪ£ Ļ│äĒÜŹĒĢśņśĆļŗż. ĻĖ░ļæźĻ│╝ ļ│┤ņØś ļŗ©ļ®┤ ņé¼ņØ┤ņ”łļŖö Ļ░üĻ░ü 350├Ś450 mmĻ│╝ 250├Ś350 mmļĪ£ ņĀüņÜ®ĒĢśņśĆļŗż. ļ│┤Ļ░ĢļÉ£ ļ¬©ļŹĖņØś ņāüņäĖļÅäļź╝ Fig. 7Ļ│╝ Fig. 8ņŚÉ Ļ░üĻ░ü ļéśĒāĆļé┤ņŚłĻ│Ā, Ļ░ĢĒīÉļ│┤Ļ░Ģņ£äņ╣śļŖö Fig. 9ņÖĆ Fig. 10ņŚÉ ļéśĒāĆļéĖ ļ░öņÖĆ Ļ░ÖņØ┤ 11ņ×ÉĒśĢ ļ│┤Ļ░ĢĻ│╝ ņĀäņ▓┤ ļ│┤Ļ░Ģņ£╝ļĪ£ Ļ│äĒÜŹĒĢśņśĆļŗż. ĒĢ┤ņäØņØĆ ņ£ĀĒĢ£ņÜöņåīĒĢ┤ņäØ ĒöäļĪ£ĻĘĖļשņØĖ ABAQUSļź╝ ņØ┤ņÜ®ĒĢśņŚ¼ ņłśĒ¢ēĒĢśņśĆļŗż. ļ│Ė ĒĢ┤ņäØņŚ░ĻĄ¼ņŚÉņä£ ņĮśĒü¼ļ”¼ĒŖĖņÖĆ Ļ░ĢĒīÉņØĆ Solid ņÜöņåī, ņ▓ĀĻĘ╝ wire ņÜöņåīļź╝ ņé¼ņÜ®ĒĢśņśĆļŗż. ļśÉĒĢ£, ņ▓ĀĻĘ╝ņĮśĒü¼ļ”¼ĒŖĖ ļé┤ņŚÉņä£ ņ▓ĀĻĘ╝Ļ│╝ ņĮśĒü¼ļ”¼ĒŖĖņØś ņØ╝ņ▓┤Ļ▒░ļÅÖņØä Ēæ£ĒśäĒĢśĻĖ░ ņ£äĒĢśņŚ¼ Embedded region ņÜöņåīļź╝ ņé¼ņÜ®ĒĢśņśĆļŗż. Ļ▓ĮĻ│äņĪ░Ļ▒┤ņØĆ ĻĖ░ļæźņØś ņ¢æļŗ©ņØä pinņ£╝ļĪ£ ņäżņĀĢĒĢśņśĆĻ│Ā, ļ│┤ ņ¢æļŗ©ņŚÉņä£ ļ│Ćņ£äļ▓ĢņØä ņé¼ņÜ®ĒĢśņŚ¼ ņĄ£ļīĆ ┬▒80 mmĻ╣īņ¦Ć Ļ░ĆļĀź ĒĢśņśĆļŗż. ņĮśĒü¼ļ”¼ĒŖĖņØś MeshļŖö ABAQUSņŚÉņä£ ņØ╝ļ░śņĀüņ£╝ļĪ£ ņ¦ĆņøÉĒĢśļŖö C3D8R, ņ▓ĀĻĘ╝Ļ│╝ Ļ░ĢĒīÉņØĆ T3D2ņ£╝ļĪ£ ņäżņĀĢĒĢśņśĆļŗż
Test model
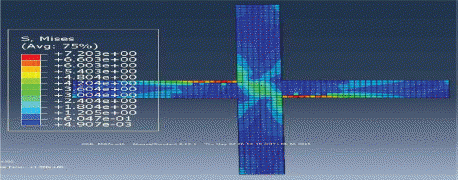
ļ│┤Ļ░ĢĒĢśņ¦Ć ņĢŖņØĆ ļ¬©ļŹĖņØś ņØæļĀźļČäĒżļÅäļź╝ Fig. 10ņŚÉ ļéśĒāĆļé┤ņŚłĻ│Ā ļ│┤Ļ░ĢļÉ£ ļ¬©ļŹĖņØś ņØæļĀźļČäĒżļÅäļź╝ Fig. 11ļČĆĒä░ Fig. 14Ļ╣īņ¦Ć ļéśĒāĆļé┤ņŚłļŗż. ļ│┤Ļ░ĢĒĢśņ¦Ć ņĢŖņØĆ ļ¬©ļŹĖņØś ĒĢ┤ņäØ Ļ▓░Ļ│╝ļź╝ ņé┤ĒÄ┤ļ│┤ļ®┤ ņØæļĀźņØ┤ ņŻ╝ļĪ£ ņĀæĒĢ®ļČĆ ļīĆĻ░üņäĀ ļ░®Ē¢źņ£╝ļĪ£ ņ¦æņżæļÉśņ¢┤ ļéśĒāĆļé¼ļŗż.
Fig. 11ņØä ņé┤ĒÄ┤ļ│┤ļ®┤ ņØæļĀźņ¦æņżæ ņāØĻĖ░ļŖö ņ¦ĆņĀÉņØ┤ ņżæņŗ¼ņĀÉņ£╝ļĪ£ ļīĆņ╣ŁĒĢśļŖö ņ£äņ╣śņÖĆ ņØ╝ņ╣śĒĢ£ļŗż. ņØ┤ Ļ▓░Ļ│╝ļŖö ņé¼ņØĖņן ĻĘĀņŚ┤ņØ┤ ņØ╝ņ¢┤ļéśļŖö Ļ▓āņØä ņ”Øļ¬ģĒĢśņśĆļŗż.
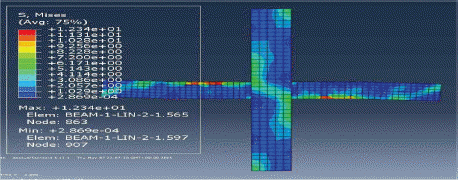
ļ│┤Ļ░ĢļÉ£ ļ¬©ļŹĖļōżņØś ņØæļĀźļČäĒżļź╝ ļ│┤ļ®┤ ņØæļĀźņØ┤ ņ¦æņżæļÉśļŖö ļČĆļČäņØ┤ ļ│┤ņØś ņ¢æļŗ© ļ░®Ē¢źņ£╝ļĪ£ ņØ┤ļÅÖĒĢśņśĆļŗż. ļ│┤Ļ░ĢĒĢśņ¦Ć ņĢŖņØĆ ļ¬©ļŹĖ ļ│┤ļŗż ļ│┤Ļ░ĢļÉ£ ļ¬©ļŹĖņØś ļ│┤ņÖĆ ĻĖ░ļæź ļüØļŗ©ņŚÉņä£ ņØæļĀźņØ┤ ņ¦æņżæļÉśņ¢┤ ļéśĒāĆļé¼ļŗż. ļśÉĒĢ£ ņé¼ņØĖņן ĻĘĀņŚ┤ņØś ĒśäņāüņØĆ ļ│┤Ļ░ĢĒĢśņ¦Ć ņĢŖņØĆ ļ¬©ļŹĖ ļ│┤ļŗż ņāüļŗ╣Ē׳ Ļ░£ņäĀļÉśņŚłļŗż. ļö░ļØ╝ņä£ ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ ņĀ£ņŗ£ĒĢ£ ļ│┤Ļ░Ģļ░®ļ▓ĢņØä ĒåĄĒĢ┤ ļ│┤-ĻĖ░ļæź ņĀæĒĢ®ļČĆ ņżæņŗ¼ņŚÉ ņØæļĀź ņ¦æņżæņØ┤ ņØ╝ņ¢┤ļéśļŖö Ļ▓āņØä ļ░®ņ¦ĆĒĢśĻ│Ā ļé┤ļĀźņØä Ēü¼Ļ▓ī Ē¢źņāü ņŗ£Ēé¼ ņłś ņ׳ņØä Ļ▓āņ£╝ļĪ£ ĒīÉļŗ©ļÉ£ļŗż.
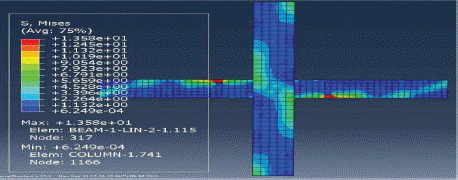
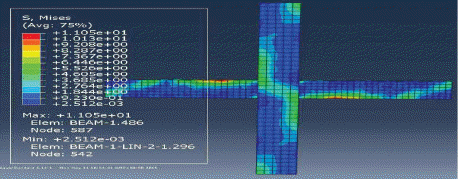
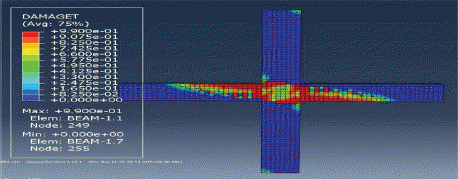
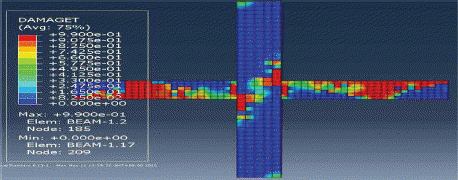
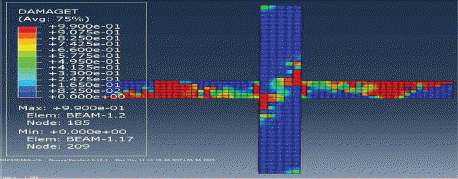
ĒĢ┤ņäØĻ▓░Ļ│╝ ļéśĒāĆļé£ ļ¬©ļŹĖļōżņØś ĒīīĻ┤┤ļ¬©ļō£ļź╝ Fig. 16ļČĆĒä░ Fig. 20ņŚÉ ļéśĒāĆļé┤ņŚłļŗż. ļ│┤Ļ░ĢĒĢśņ¦Ć ņĢŖņØĆ ļ¬©ļŹĖĻ│╝ ļ│┤Ļ░ĢļÉ£ ļ¬©ļŹĖļōżņØś ĒīīĻ┤┤ ļ¬©ļō£ļŖö ņä£ļĪ£ ļŗżļźĖ Ļ▓ĮĒ¢źņØä ļ│┤ņŚ¼ņŻ╝ņŚłļŗż. ABAQUSņŚÉņä£ ļ¬©ļŹĖņØś ĻĘĀņŚ┤ņĀĢļÅäļź╝ DAMAGET ņäżņĀĢņØä ņØ┤ņÜ®ĒĢśņŚ¼ ĒÖĢņØĖĒĢĀ ņłś ņ׳ļŖöļŹ░, ļ│┤Ļ░ĢĒĢśņ¦Ć ņĢŖņØĆ ļ¬©ļŹĖņØĆ ļ│┤-ĻĖ░ļæź ņĀæĒĢ®ļČĆņŚÉņä£ ņé¼ņØĖņן ĻĘĀņŚ┤ņØ┤ ĒśĢņä▒ļÉśņŚłļŗż. ņĀäņ▓┤ņĀüņ£╝ļĪ£ ĻĘĀņŚ┤ņĀĢļÅäļŖö ņĀæĒĢ®ļČĆ ņżæņŗ¼ņ£╝ļĪ£ ļīĆĻ░üņäĀņ£╝ļĪ£ ļČäĒżĒĢśņśĆļŗż. ļ░śļ®┤ ļ│┤Ļ░ĢļÉ£ ļ¬©ļŹĖļōżņØĆ ņĀæĒĢ®ļČĆņØś ļ│┤Ļ░Ģ Ļ░ĢĒīÉņ£╝ļĪ£ ņØĖĒĢśņŚ¼ ņĀæĒĢ®ļČĆņŚÉņä£ņØś ĻĘĀņŚ┤ņĀĢļÅäĻ░Ć ļ│┤Ļ░ĢĒĢśņ¦Ć ņĢŖļŖö ļ¬©ļŹĖņŚÉ ļ╣äĒĢ┤ ļ»Ėļ╣äĒĢśņśĆļŗż. ļśÉĒĢ£ ļ│┤Ļ░ĢļÉ£ ļ¬©ļŹĖļōż ņżæņŚÉņä£ļÅä ļæÉĻ╗ś 6 mmņØś Ļ░ĢĒīÉņØä ņé¼ņÜ®ĒĢ£ ļ¬©ļŹĖņØ┤ Ļ░Ćņן ņóŗņØĆ ņä▒ļŖźņØä ļ│┤ņŚ¼ņŻ╝ņŚłļŗż. ļ│┤Ļ░Ģ Ļ░ĢĒīÉņØś Ēü¼ĻĖ░ņŚÉ ļö░ļźĖ ļ│ĆņłśĒĢ┤ņäØĻ▓░Ļ│╝, Fig. 21ņŚÉ ļ│┤ļŖö ļ░öņÖĆ Ļ░ÖņØ┤ ļ│┤Ļ░Ģ Ļ░ĢĒīÉņØś Ēü¼ĻĖ░Ļ░Ć ņĮśĒü¼ļ”¼ĒŖĖņØś ĻĘĀņŚ┤ņŚÉ ļ»Ėņ╣śļŖö ņśüĒ¢źņØ┤ ļ»Ėļ╣äĒĢ£ Ļ▓āņ£╝ļĪ£ ļéśĒāĆļé¼ļŗż.
ļ¬©ļōĀ ļ¬©ļŹĖņØś ĒĢśņżæ-ļ│Ćņ£äĻ│ĪņäĀĻ│╝ ņĄ£ļīĆĒĢśņżæ ļ░Å ņĄ£ļīĆļ│Ćņ£äļź╝ Fig. 21Ļ│╝ Table 2ņŚÉ Ļ░üĻ░ü ļéśĒāĆļé┤ņŚłļŗż. ļ¬©ļōĀ ļ│┤Ļ░ĢļÉ£ ļ¬©ļŹĖņØś ņĄ£ļīĆ ļ│Ćņ£äļŖö ļ│┤Ļ░ĢĒĢśņ¦Ć ņĢŖņØĆ ļ¬©ļŹĖņŚÉ ļ╣äĒĢśņŚ¼ 5~9 mm ņĀĢļÅä ņ”ØĻ░ĆĒĢśņśĆļŗż. ņØ┤Ļ▓āņØĆ ļ│┤Ļ░ĢĻ░ĢĒīÉņØ┤ Ļ░Ćņ¦ĆĻ│Ā ņ׳ļŖö ņŚ░ņä▒ļŖźļĀź ļĢīļ¼ĖņŚÉ ņĄ£ļīĆļ│Ćņ£äĻ░Ć ņ”ØĻ░ĆļÉ£ Ļ▓āņ£╝ļĪ£ ĒīÉļŗ©ļÉ£ļŗż. ļ¬©ļŹĖ RD1-1Ļ│╝ ļ¬©ļŹĖ RD2-1ļź╝ ļ╣äĻĄÉĒĢśņŚ¼ ņé┤ĒÄ┤ļ│┤ļ®┤, ļ│┤Ļ░Ģ ļ®┤ņĀüņØ┤ ņ”ØĻ░ĆĒĢ©ņŚÉ ļö░ļØ╝ ļ¬©ļŹĖļōż Ļ░äņØś ņĄ£ļīĆļé┤ļĀź ļ░Å ņĄ£ļīĆ ļ│Ćņ£äļŖö Ļ▒░ņØś ņ░©ņØ┤ļź╝ ļ│┤ņØ┤ņ¦Ć ņĢŖņĢśļŗż. ļ░śļ®┤ ļ¬©ļŹĖ RD1-1Ļ│╝ RD1-2ļź╝ ļ╣äĻĄÉĒĢśņŚ¼ ņé┤ĒÄ┤ļ│┤ļ®┤, ļ│┤Ļ░Ģ Ļ░ĢĒīÉņØś ļæÉĻ╗śļź╝ ņ”ØĻ░Ćņŗ£Ēé┤ņŚÉ ļö░ļØ╝ ļ¬©ļŹĖņØś ļé┤ļĀźņØĆ ņ”ØĻ░ĆĒĢśņśĆļŗż. ļö░ļØ╝ņä£ ļ│┤Ļ░ĢĒÜ©Ļ│╝ņŚÉ ļīĆĒĢ┤ņä£ļŖö Ļ░ĢĒīÉņØś Ēü¼ĻĖ░ ļ│┤ļŗżļŖö Ļ░ĢĒīÉņØś ļæÉĻ╗śļĪ£ ņØĖĒĢ┤ ļŹö Ēü░ ņśüĒ¢źņØ┤ ņ׳ļŗżĻ│Ā ĒīÉļŗ©ļÉ£ļŗż. ĒĢśņ¦Ćļ¦ī ļ¬©ļŹĖ RD2-2ņØś Ļ▓ĮņÜ░ ņĄ£ļīĆ ļé┤ļĀźņØĆ Ļ░Ćņן Ēü¼ņ¦Ćļ¦ī Ļ░Ćņן ļ©╝ņĀĆ ĻĘĀņŚ┤ņØ┤ ļ░£ņāØĒĢśņśĆļŗż. ņØ┤ļŖö Ļ░ĢĒīÉ ļæÉĻ╗śļź╝ ļäłļ¼┤ Ļ│╝ļīĆĒĢśĻ▓ī ņ”ØĻ░Ćņŗ£Ēéżļ®┤ ņ×ÉņżæņØ┤ ņ╗żņ¦ĆĻ│Ā Ļ░ĢĒīÉĻ│╝ ņ▓ĀĻĘ╝ņĮśĒü¼ļ”¼ĒŖĖ ņé¼ņØ┤ņØś ļČĆņ░®ļĀźņØ┤ ļ¢©ņ¢┤ņ¦ĆĻĖ░ ļĢīļ¼ĖņŚÉ ļ│┤Ļ░ĢĒÜ©Ļ│╝Ļ░Ć ņĀĆĒĢśļÉśļŖö Ļ▓āņ£╝ļĪ£ ĒīÉļŗ©ļÉ£ļŗż. ļö░ļØ╝ņä£ ļ│┤Ļ░ĢĻ░ĢĒīÉņØś ļæÉĻ╗śļŖö 6~8 mmņĀĢļÅäļĪ£ ĒĢśļŖö Ļ▓āņØ┤ Ļ░Ćņן ņÜ░ņłśĒĢ£ ļ│┤Ļ░ĢĒÜ©Ļ│╝ļź╝ ļéśĒāĆļé┤ļŖö Ļ▓āņ£╝ļĪ£ ņé¼ļŻīļÉ£ļŗż.
ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö ņ▓ĀĻĘ╝ņĮśĒü¼ļ”¼ĒŖĖ ļ│┤-ĻĖ░ļæź ņĀæĒĢ®ļČĆ Ļ░ĢĒīÉļ│┤Ļ░ĢĻ│Ąļ▓ĢņØś ļ│┤Ļ░ĢĒÜ©Ļ│╝ņŚÉ ļīĆĒĢ┤ ĒÅēĻ░ĆĒĢśĻĖ░ ņ£äĒĢ┤ ņ£ĀĒĢ£ņÜöņåīĒĢ┤ņäØ ĒöäļĪ£ĻĘĖļשņØĖ ABAQUSļź╝ ņé¼ņÜ®ĒĢśņŚ¼ ĒĢ┤ņäØņŚ░ĻĄ¼ļź╝ ņłśĒ¢ēĒĢ£ Ļ▓░Ļ│╝ ļŗżņØīĻ│╝ Ļ░ÖņØĆ Ļ▓░Ļ│╝ļź╝ ņ¢╗ņŚłļŗż.
1. ņ▓ĀĻĘ╝ņĮśĒü¼ļ”¼ĒŖĖ ļ│┤-ĻĖ░ļæź ņĀæĒĢ®ļČĆņŚÉ Ļ░ĢĒīÉņ£╝ļĪ£ ļ│┤Ļ░Ģ ĒĢĀ Ļ▓ĮņÜ░ ļ╣äļ│┤Ļ░Ģ ņŗżĒŚśņ▓┤ļź╝ ĻĖ░ņżĆņ£╝ļĪ£ ņĢĮ 63~97.6% ļé┤ļĀźņØ┤ Ē¢źņāüļÉśņŚłļŗż.
2. Ļ░ĢĒīÉļ│┤Ļ░Ģ ņŗ£ ļ│┤-ĻĖ░ļæź ņĀæĒĢ®ļČĆņŚÉņä£ ņØæļĀźņ¦æņżæņØä ļ¦ēĻ│Ā ņĀæĒĢ®ļČĆņØś ĻĘĀņŚ┤ņØ┤ ņĀüĻ▓ī ļéśĒāĆļé¼ļŗż. ļö░ļØ╝ņä£ ĻĄ¼ņĪ░ļ¼╝ņØś ļ│┤-ĻĖ░ļæź ņĀæĒĢ®ļČĆĻ░Ć ļ©╝ņĀĆ ĒīīĻ┤┤ļÉśļŖö ņ¢æņāüņØä Ēö╝ĒĢĀ ņłś ņ׳ņŚłļŗż.
3. Ļ░ĢĒīÉļ│┤Ļ░Ģ ņŗ£ ļ│┤Ļ░Ģļ®┤ņĀüņØä ņ”ØĻ░Ćņŗ£ĒéżļŖö Ļ▓āļ│┤ļŗż Ļ░ĢĒīÉņØś ļæÉĻ╗śļź╝ ņ”ØĻ░Ćņŗ£ĒéżļŖö Ļ▓āņØ┤ ĻĘĀņŚ┤ļ░®ņ¦Ćļéś ļé┤ļĀźņ”ØĻ░ĆĻ░Ć Ēü¼Ļ▓ī ļéśĒāĆļéś ļŹö ņÜ░ņłśĒĢ£ ļ│┤Ļ░Ģņä▒ļŖźņØä ļ│┤ņśĆļŗż.
4. ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ ņĀ£ņŗ£ĒĢ£ ļ│┤Ļ░Ģļ░®ļ▓ĢņØ┤ ņ▓ĀĻĘ╝ņĮśĒü¼ļ”¼ĒŖĖ ĻĄ¼ņĪ░ļ¼╝ņØś ļ│┤-ĻĖ░ļæź ņĀæĒĢ®ļČĆņŚÉņä£ ņØæļĀź ņ¦æņżæņØä ļ░®ņ¦ĆĒĢśĻ│Ā ļé┤ļĀźņØä Ēü¼Ļ▓ī Ē¢źņāüņŗ£Ēé¼ ņłś ņ׳ņØä Ļ▓āņ£╝ļĪ£ ņé¼ļŻīļÉ£ļŗż.
Ļ░Éņé¼ņØś ĻĖĆ
ļ│Ė ņŚ░ĻĄ¼ļŖö ĻĄŁĒåĀĻĄÉĒåĄļČĆ ļÅäņŗ£Ļ▒┤ņČĢ ņŚ░ĻĄ¼Ļ░£ļ░£ņé¼ņŚģņØś ņŚ░ĻĄ¼ļ╣äņ¦ĆņøÉ(13AUDP-B066083-01)ņŚÉ ņØśĒĢ┤ ņłśĒ¢ēļÉśņŚłņŖĄļŗłļŗż
References
Hong, Geonho (2005) Repair and Strengthening of Reinforced Concrete Beam-Column Joints: State of the Art. KCI concrete journal, No. 17, Vol. 4, pp. 57-67.

Kim, E, Han, S, Park, Y, and Suh, B (2006) Seismic Retrofit Effects of RC Piers Strengthened with Steel Jacketing using FEM. Journal of the Korean Society of Civil Engineers, pp. 1822-1836.

Kim, Taehoon, and Shin, Hyunmock (2006) Seismic Performance Assessment of Reinforced Concrete Bridge Columns using Nonlinear Finite Element Analysis. Journal of the Korean Society of Civil Engineers, No. 10, Vol. 3, pp. 21-33.

Liu, Y (2003). Deformation Behavior Experiment Study of RC Frame Beam-column Joints Strengthened by Gluing steel. For the Degree of Master of Science.

- TOOLS
-
METRICS

-
- 0 Crossref
- 3,204 View
- 98 Download
- Related articles in KOSHAM
-
A Study on the Reinforcement of Bridge Foundation in the Limestone Cavity2011 February;11(1)