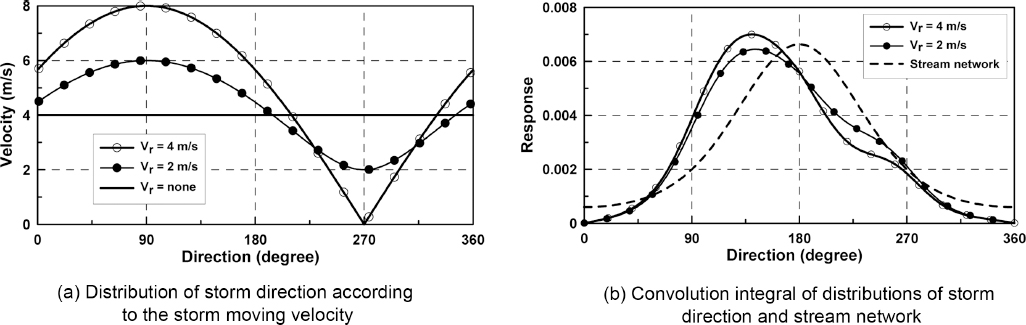
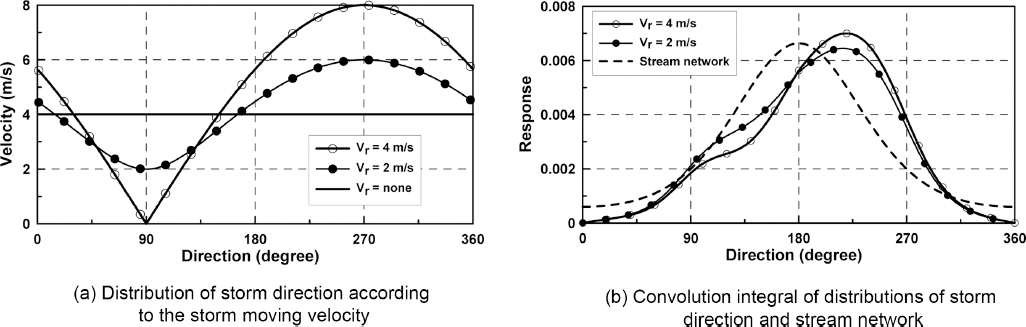
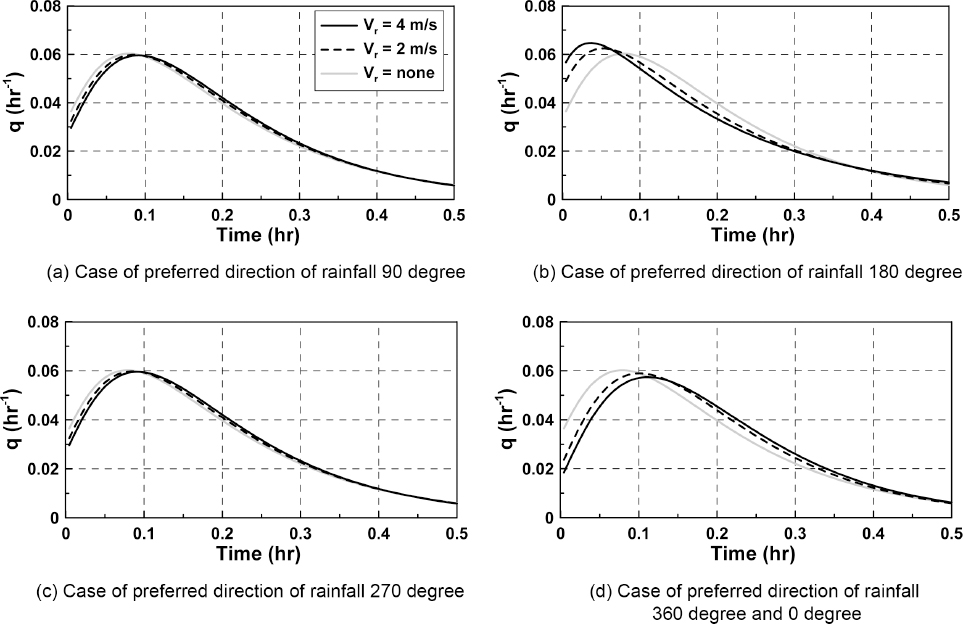
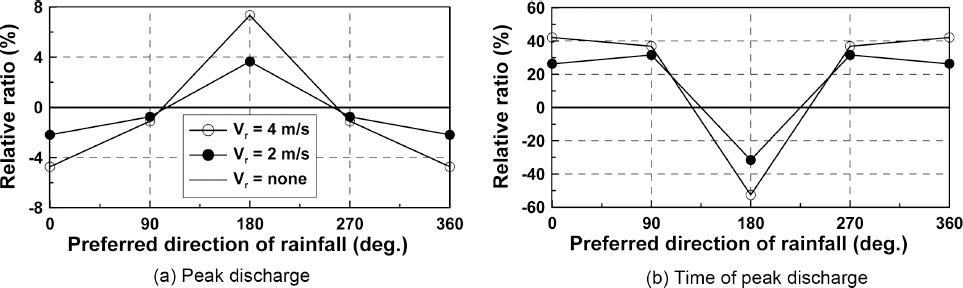
Anderson, H.S, Jacobsen, P, and Harrmo√ęs, P (1991) The Effect of Rainfall Movement on Peak Flow in Sewers.
Atmospheric Research, Vol. 27, pp. 129-135. 10.1016/0169-8095(91)90013-M.

Brierley, G.J, and Fryirs, K.A (2005).
Geomorphology and River Management. Wiley-Blackwell.

Chang, C.L (2007) Influence of Moving Rainstorms on Watershed Responses.
Environmental Engineering Science, Vol. 27, No. 10, pp. 1353-1360. 10.1089/ees.2006.0220.

Choi, G.W, Lee, H.S, and Ahn, S.J (1993) Simulation of Moving Storm in a Watershed Using A Distributed Model(II)- Model Application-.
Journal of Korea Water Resources Association, Vol. 26, No. No. 1, pp. 81-91.

Choi, G.W, Kang, H.K, and Park, Y.S (2000) A Study on Runoff Characteristics by the Moving Storm in the Watershed using GIS.
Journal of Korea Water Resources Association, Vol. 33, No. No. 6, pp. 793-804.

Foroud, N, Broughton, R.S, and Austin, G.L (1984) The Effects of a Moving Rainstorm on Direct Runoff Properties.
Water Resources Bulletin, Vol. 20, No. No. 1, pp. 87-91. 10.1111/j.1752-1688.1984.tb04645.x.

Gupta, V.K, Waymire, E, and Wang, C.T (1980) A Representation of an Instantaneous Unit Hydrograph from Geomorphology.
Water Resources Research, Vol. 16, No. No. 5, pp. 855-862. 10.1029/WR016i005p00855.

Han, K.Y, Jeon, M.W, and Choi, K.H (2004) Runoff Analysis due to the Moving Storm.
Journal of Korea Water Resources Association, Vol. 37, No. No. 10, pp. 823-836. 10.3741/JKWRA.2004.37.10.823.

Han, K.Y, Jeon, M.W, and Kim, J.S (2006) Runoff Analysis due to Moving Storms based on the Basin Shapes (I) - for the Symmetric Basin Shape.
Journal of Korea Society of Civil Engineers, Vol. 26, No. No. 1B, pp. 15-25.

Lima, JLMPD, and Singh, V.P (2002) The Influence of the Pattern of Moving Rainstorms on Overland Flow.
Advanced in Water Resources, Vol. 25, No. No. 7, pp. 817-828. 10.1016/S0309-1708(02)00067-2.

Lima, J.L.M.P.D, and Singh, V.P (2003) Laboratory Experiments on the Influence of Storm Movement on Overland Flow.
Physics and Chemistry of the Earth, Vol. 28, pp. 277-282. 10.1016/S1474-7065(03)00038-X.

Lima, J.L.M.P.D, Singh, V.P, and Lima, M.I.P.D (2003) The Influence of Storm Movement on Water Erosion: Storm Direction and Velocity Effects.
Catena, Vol, Vol. 52, No. No. 1, pp. 39-56. 10.1016/S0341-8162(02)00149-2.

Lima, J.L.M.P.D, Souza, C.S, and Singh, V.P (2008) Granulometric Characterization of Sediments Transported by Surface Runoff Generated by Moving Storms.
Nonlinear Processes in Geophysics, Vol. 15, pp. 999-1011. 10.5194/npg-15-999-2008.

Niemczynowicz, J (1984) Investigation of the Influence of Rainfall Movement on Runoff Hydrograph. Part ?. Simulation on Conceptual Catchment.
Nordic Hydrology, Vol. 15, pp. 57-70.

Oh, K.D, Lee, S.C, Ahn, W.S, Ryu, Y.H, and Lee, J.H (2010) A Study on Design Flood Analysis Using Moving Storms.
Journal of Korea Water Resources Association, Vol. 43, No. No. 2, pp. 167-185. 10.3741/JKWRA.2010.43.2.167.

Park, C, and Yoo, C (2011) Quantification of Storm Direction for a River Basin.
Journal of the Korean Society of Hazard Mitigation, Vol. 10, No. No. 6, pp. 109-117.

Sargent, D.M (1981) An Investigation into the Effects of Storm Movement on the Design of Urban Drainage Systems: Part 1.
The Public Health Engineer, Vol. 9, pp. 201-207.

Sargent, D.M (1982) An Investigation into the Effects of Storm Movement on the Design of Urban Drainage Systems: Part 2. Probability Analysis.
The Public Health Engineer, Vol. 10, pp. 111-117.

Singh, V.P (1998) Effect of the Direction of Storm Movement on Planar Flow.
Hydrological Processes, Vol. 12, No. No. 1, pp. 147-170. 10.1002/(SICI)1099-1085(199801)12:1<147::AID-HYP568>3.3.CO;2-B.

Singh, V.P (2002) Effect of the Duration and Direction of Storm Movement on Infiltrating Planar Flow with Full Areal Coverage.
Hydrological Processes, Vol. 16, No. No. 7, pp. 1479-1511. 10.1002/hyp.358.

Surkan, A.J (1974) Simulation of Storm Velocity Effects of Flow from Distributed Channel Network.
Water Resources Research, Vol. 10, No. No. 6, pp. 1149-1160. 10.1029/WR010i006p01149.

Townson, J.M, and Sim, O.H (1974) A Laboratory Study of Runoff Caused by Line Storm Moving over a Conceptual Catchment.
Water Services, pp. 266-269.

Yen, B.C, and Chow, V.T (1969) A Laboratory Study of Surface Runoff due to Moving Rainstorms.
Water Resources Research, Vol. 5, No. No. 5, pp. 989-1006. 10.1029/WR005i005p00989.

Zevenbergen, L.W, and Thorne, C.R (1987) Quantitative Analysis of Land Surface Topography.
Earth Surface Processes and Landforms, Vol. 12, pp. 47-56. 10.1002/esp.3290120107.