|
 |
- Search
| J. Korean Soc. Hazard Mitig. > Volume 18(2); 2018 > Article |
|
Abstract
Estimation of probability precipitation for the design of hydraulics structure is an important factor in determining the strength and scale. Generally, we use probability precipitation through the assumption of stationarity. Regional impact of climate change causes the necessity of the nonstationary probability rainfall estimation. Several nonlinear regression methods were applied to deal with the nonstationary behavior of extreme rainfall effectively by modeling the variability of the location and scale parameters of future extreme probability distribution. These regression models have drawback of forcing future change shape according to the regression types. In this study, the variability of the probable maximum rainfall for different durations in target years at Seoul was analyzed with different approaches such as logistic regression, power regression, and neural networks using GCM data associated with different green house gas emission scenarios. The increasing ratio of the future hourly probability rainfall using NN is larger than that using Logistic and Power models, and the increasing ratio of the future 24hr probability rainfall using NN is smaller than that using Logistic and Power models.
ěě§
ě´ěě ěšě 몊ě ě ě곾꾏쥰돟 ě¤ęłëĽź ěí íëĽ ę°ěë ě°ě ě 꾏쥰돟ě ę°ëě ęˇëŞ¨ëĽź 결ě íë ě¤ěí ěěě´ë¤. 기íëłíě ě§ěě ěíĽěźëĄ ě¸í´ ëšě ěěą íëĽ ę°ěë ě°ě ě íěę° ëëëęł ěë¤. ëšě ěěąě ę°ě§ë ꡚěšę°ěë ëłë íšěąě í¨ęłźě ěźëĄ ëěí기 ěíěŹ ëŻ¸ë ꡚěšíëĽ ëśíŹíě ěěš ë° íěęłěě ëłëíšěąě ëíěŹ ę°ě˘
ëšě í íęˇëިíě ě ěŠíěŹ ëŞ¨íííë 기ë˛ë¤ě´ ě ěëěë¤. ě´ëŹí ëšě ííęˇëިíë¤ě ě ěŠě ęˇšěš ěë ´íšěąě´ ě ěŠ ę¸°ë˛ě ë°ëź ěŹě ě ě í´ě§ë ë¨ě ě´ ěë¤. 본 ě°ęľŹěěë Logistic íęˇëިí, Power íęˇëިíě ě´ěŠíěŹ ě°ě í ěě¸ě§ě 몊íě°ëëł, ě§ěěę°ëł íëĽ ę°ěë 결곟ě ě¸ęłľě ę˛˝ë§ ę¸°ë˛ęłź ě¨ě¤ę°ě¤ ë°°ěśěë댏ě¤ëł GCM ěëŁëĽź ě´ěŠí 몊íě°ëëł, ě§ěěę°ëł íëĽ ę°ěëě ëšęľ ëśěíěë¤. 본 ě°ęľŹě ěŹěŠë ě¸ęłľě ę˛˝ë§ ę¸°ë˛ě ë°ëĽ¸ 미ë íëĽ ę°ě°ëě Logistic, Power 모í ě ěŠě ë°ëĽ¸ 미ë íëĽ ę°ě°ëě ëšíěŹ 1ěę° íëĽ ę°ě°ëě ěŚę°ě¨ě´ íŹę˛ ëíëŹěźëŠ°, 24ěę° íëĽ ę°ě°ëě ëí´ěë ěëě ěźëĄ ěŚę°ě¨ě´ ěę˛ ëíëŹë¤.
ě¸ęł ę° ęľěěë 기íëłíě ěí í경ëłíě ëěíęł ě 기íëłíëĄ ě¸í ě§ěě ěíĽě ëí íę°, ě츥, ě ěą
ě댽 ëąě ěí´ ěŹëŹ ëśěźěě ě°ęľŹę° ě´ëŁ¨ě´ě§ęł ěěźëŠ° 기íëłí ëě ěě¤í
꾏ěśě íě ě ě¸ęłě ěźëĄ ě§ëŠ´íęł ěë ě¤ěí ęłźě ę° ëěë¤. 기íëłíě ę´ë ¨í ě돸íěě ëłí íšěą ě¤ěě í¸ě°íšěąě ëłíëĄ ě¸í ěěŹí´ íšěąě ëłíę° íě¤íëęł ěë ěíŠěě 미ëě ꡚěšę°ěë íšěąëłí뼟 ëśěíęł ě츥í기 ěí ěŹëŹ ě°ęľŹę° ěíëęł ěë ěíŠě´ë¤. IPCC(2014) 5ě°¨ëł´ęł ěě ë°ëĽ´ëŠ´ ě§ęľŹíęˇ ę¸°ě¨ě´ 112ë
(1901-2012) ëě ě˝ 0.89â ěěšíěë¤. ě´ë 4ě°¨ëł´ęł ě 100ë
(906-2005) ëě 0.74â ěěší ę˛ęłź ëšęľí´ ëłź ë ě§ęľŹě íęˇ ę¸°ě¨ ěěšě´ ę°ěíëęł ěë¤ë ę˛ě´ë¤. ě§ęľŹě íęˇ ę¸°ě¨ëżë§ ěëëź í´ě늴 ěěš ëí ę°ěíëęł ěěźëŠ° 2100ë
ěë 기ě¨ě´ ě˝ 3.7â ěŚę°í늰 í´ě늴ě ě˝ 63 cm ěŚę°í ę˛ě´ëźęł ě ë§íěë¤. ëí ě§ě¤í¸ě°, ëë°Šíě, ę°ë ëą ě´ě기í íěě ěí ě¸ëŞ
ë° ę˛˝ě ě íźí´ë ěŚę°íęł ěěźëŠ° ěě°ěŹí´ ë°ěęłź ęˇëި ëí ěŚę°íęł ěë ěśě¸ëĽź ëł´ě´ęł ěë¤(KMA, 2015). ě´ëŹí 기íëłí ěśě¸ëĽź ęł ë ¤íěě ë ě곾꾏쥰돟곟 ë°°ěěě¤ ëą ě댏â
ě돸 ěě¤ ě¤ęłě ěźë°ě ě¸ ë°Šë˛ěźëĄ ě°ě ë ě¤ęł ę°ěëě ě ěŠě íęłëĽź ę°ě§ë¤. ěľęˇźěë ę°ěě ě ěěąě ę°ě í ěěěę´ëŚŹ ěě¤í
ě´ěě ěě´ ęˇźëě ęˇšěš ę°ěëě ëłí íšěąě ëšěśě´ ëłź ë ę°ě ě ěěąě 기ě´í ě íľě ě¸ ëšëí´ěě íľí´ ě°ě ë ě¤ęł ę°ěëě ě ěŠě ëíěŹ íëšěą ěŹę˛í ę° ě꾏ëęł ěë¤(Kwon and Kim, 2009; Jang et al., 2011). ě´ëŹí ě°ęľŹę˛°ęłźë¤ëĄ ě¸íěŹ ęˇšěšę°ěë í본ěëŁě íęˇ , ëśě° ëą íľęłíšěąě´ ěę°ě´ ě§ë¨ě ë°ëź ëłííë ëšě ěěąě ęł ë ¤í ëšëí´ěě íěěąě´ 죟ěĽëęł ěë¤. ëšě ěěą ëšëí´ěě 매ę°ëłěë ëśíŹę° ëłíí기 ë돸ě 기쥴ě ě ěěąě ę°ě í ëšëí´ěęłź ë¤ëĽ¸ ě ꡟë˛ě´ íěíë¤. ëí íšě ěŹí기ę°ě ꡚěšěŹěě ěśě í기 ěí´ ě돸íě ěęłě´ ěëŁëĽź 모íííë íľęłíě ë°Šë˛ě ěëŁě ëšě ěěąě ęł ë ¤í ě ěë¤. ęłźęą°ëśí° íěŹęšě§ ë§ě ě°ęľŹěë¤ě ěí´ ę°ěěëŁě ëšě ěěąě ęł ë ¤í ę°ěëšëí´ěě ěíěŹ ęˇšěšëśíŹě 매ę°ëłě ěśě 기ë˛, ëšě ěěą ëšëí´ě ę¸°ë˛ ëą ë¤ěí ě°ęľŹę° ěíëěë¤(Leclerc and Ouarda, 2007; Hanel and Buishand, 2010; Villarini et al., 2010; Shin et al., 2008; Zhang et al., 2014).
ęľë´ě¸ěě ę°ě ěëŁě ëšě ěěą ëšëí´ěě íľí íëĽ ę°ěë ě°ě ęłź ę´ë ¨í ě°ęľŹę° íë°í ě´ëŁ¨ě´ě§ęł ěë¤. ęľě¸ě ě°ęľŹëíĽě He et al.(2006)ě Gumbel ëśíŹ ë° Log Pearson Type-III ëśíŹě 매ę°ëłě ëłíě ëíěŹ íęˇëśěě íľí´ íěëšë í´ěě íěěźëŠ° Renard et al.(2006)ě Bayesian 기ë˛ě ěŹëŹ ę°ě§ě ꡚěšëśíŹí(exponential, Generalized Pareto(GP), Gumbel, Generalized Extreme Value)ě ě ěŠíěë¤. Sugahara et al.(2009)ě Peaks-Over-Threshold(POT)ě GP ëśíŹëĽź ě´ěŠíěŹ Brazil Sao Paulo ě§ěě 1933ë
-2005ë
ęšě§ ěźę°ěë ęˇšěš ëšëí´ěě íěěźëŠ° ëšëިěě ěśě¸ę˛ě ě ěíěŹ Mann-Kendall ę˛ě ě ěííěë¤. ęľë´ě ě°ęľŹ ëíĽě Kwon et al.(2009)ě 매ë
ę°ě°ěëŁę° ěśę°ë기 ë돸ě Gumbel ëśíŹě 매ę°ëłěę° ëłííęł ę˛°ęłźě ěźëĄ íëĽ ę°ěëě´ ëłííë ě ě ę°ěíěŹ ě´ę¸° 20ë
ě 기ě¤ěźëĄ 1ë
ěŠ ëě í늴ě ëě íęˇ ęłź 매ę°ëłěě ěę´ę´ęłëĽź ě´ěŠíěŹ íëĽ ę°ěëě ě°ě íěë¤. Kim et al.(2012)ě´ ě´ę¸° 20ë
ě 기ě¤ěźëĄ 1ë
ěŠ ëě í ëě íęˇ ě° ěľë ę°ěëě ë°ëź ěęłę°ě ëłí뼟 ęł ë ¤íěŹ ěśěśë ěëŁě ěŹí기ę°ëł íëĽ ę°ěëě ëšęľëśěě íľí´ ěęłę°ě ëłíę° ě°ęľŹę˛°ęłźě 미ěšë ěíĽë Ľě ě ěíęł ëśíŹě ííě ë°ëĽ¸ ěęłę°ě 믟ę°ë ě°¨ě´ëĽź ëšęľ ëśěíěŹ ěęłę°ě ëłíě ěíĽě ě ę˛ ë°ë ëśíŹëĽź ě ěíěë¤. Park et al.(2014)ě ëšě°ě´ęłźěš ę°ě ěëŁëĽź íěŠí ëšëí´ě ë°Šë˛ě ě ěíěěźëŠ°, Shin et al.(2013)ě RCP 8.5 ěëëŚŹě¤ ěëŁëĽź ě ěěą ëšëí´ě 결곟ě GEV ëśíŹëĽź ě´ěŠí ëšě ííęˇëĽź íľí 매ę°ëłě ěśě ęłź ě°ě ë ëšëí´ě 결곟뼟 ëšęľíěŹ ę°ęšě´ 미ëě íëĽ ę°ěëě ę˛˝ě° ëšě ěěą ëšëí´ě ę˛°ęłźę° ě íŠíë¤ęł íěë¤.
본 ě°ęľŹěěë ëšě ěěąě ęł ë ¤í ěŹí기ę°ě ë°ëĽ¸ íëĽ ę°ěëě ě°ě í기 ěíěŹ Gumbel ëśíŹëĽź ě´ěŠíěěźëŠ° 몊íě°ëě í´ëšíë Gumbel ëśíŹíě 매ę°ëłě뼟 ěśě í기 ěíěŹ ëě íęˇ ě° ěľë ę°ěë ëłíě ëí 매ę°ëłě ëłí ěę´ěąě ě°ęłíěë¤. ě´ëĽź ěíěŹ ě íě°ęľŹë¤ěě ě ěŠë ę°ě˘
íęˇëިíě ěŹěŠë 기ë˛ě ë°ëź ęˇšěš ěë ´íšěąě´ ě í´ě§ëŠ° 몊íě°ë íëĽ ę°ěëě´ ęłźęą° ěëŁě ěí´ ę˛°ě ë늰 ěŹěŠíë íęˇëިíě ë°ëź 죟ę´ě ě¸ íëĽ ę°ěëě ě°ě íë ë¨ě ě ëł´ěíęł AR5 GCM뼟 ěŹěŠíěŹ ëŻ¸ë íëĽ ę°ěë ě°ě íěŹ ę¸°ěĄ´ě íęˇëިí ě ěŠě ë°ëĽ¸ 미ëëłí뼟 ę°ě íë ë¨ě ě ę°ě íęł ě¸ě˝íë ě ꡟ밊ë˛ěźëĄë ě츥í ě ěë ě¨ě¤ę°ě¤ë°°ěśěë댏ě¤ëłëĄ íëĽ ę°ěëě ëłí뼟 ě°ě íęł ëśěíěë¤. 본 ě°ęľŹěěë 기쥴ě ě ěěąě ę°ě í íëĽ ę°ěëęłź Logistic íęˇëިí, Power íęˇëިíě ě ěŠíěŹ ě°ě í ěě¸ě§ě 몊íě°ëëł, ě§ěěę°ëł íëĽ ę°ěë 결곟ě ě¸ęłľě 경ë§ę¸°ë˛ęłź ě¨ě¤ę°ě¤ ë°°ěśěë댏ě¤ëł GCM ěëŁëĽź ě´ěŠí 몊íě°ëëł, ě§ěěę°ëł íëĽ ę°ěëě ëšęľ ëśěíěë¤.
ëšëí´ěě íľí íëĽ ę°ěë ě°ě ě ę°ěëśíŹě ꡚěšëĽź ë¤ëŁ¨ęł ěěźëŠ° ꡚěšëśíŹě í
ěź(tail)ě ěŹěŠí¨ěźëĄ ěëŁě ëł´ě 기ę°ě´ íëł´ëě§ ěěźëŠ´ ëśíŹí ě ě ě´ë 매ę°ëłě ěśě ë°Šë˛ě ë°ëź íëĽ ę°ěëě ëłëě´ íŹę˛ ëíëë ꡟ본ě ě¸ íęłëĽź ę°ě§ë¤. ë°ëźě 본 ě°ęľŹěěë ěëě ěźëĄ ěĽę¸°ę°ě ę°ěŠ ěëŁę¸°ę°ě ę°ě§ ěě¸ ě§ě ě ëěěźëĄ 1961ë
-2016ë
ę¸°ę° ëěě ěę° ë¨ěě ę°ěěëŁëĽź ě´ěŠíěë¤. 본 ě°ęľŹě ěŹěŠë GCM ěëŁë 기ěě˛ěě ě ęłľíë HadGEM2-A0(134km)ě ěíě ěě¸í뼟 íľí´ ěěąë HadGEM3-RA(12.5km) ę°ěěëŁě í¸ěëł´ě ë ěě¸ě§ě ě 미ë ę°ěë ěëŁëĄ IPCC RCP 2.6, 4.5, 6.0, 8.5 ěë댏ě¤ëłëĄ ěě§íěë¤. ěě§ë GCM ěëŁ ę¸°ę°ě 1956ë
~ 2099ë
(144ë
)ě´ëŠ° ěź ë¨ě ěëŁëĄ ě¸ęłľě ę˛˝ë§ ęľŹěąě ě
ë ĽěëŁëĽź 꾏ěśě ěíěŹ ę°ě ěěëŁ ěě°ě CM(Contraction Mapping)기ë˛ě ě ěŠíěë¤. CM기ë˛ě ę°ěěëŁě ę°ě ě기ě ěŹ ę°ě ě ě ěŠí ě ěë ěëŁě ëíěŹ ěëŁ ěŹě´ě ę°ě ěźě ëšě¨ ě´íëĄ ěśěěí¤ë í¨ěě´ë¤. í¨ě f: D ᅪ Dě ëíěŹ, ěěě x, y â Dě ëíěŹ d(f(x), f(y)) ⤠râ
d(x, y)ě¸ 0â¤r<1ę° ěĄ´ěŹíë ę˛˝ě° f뼟 (D, d) ěě ěśě˝ěŹěě´ëźęł íë¤(Banach, 1922). Fig. 1ě ëěíë CM기ë˛ě downscaling ęłźě ě ëíë¸ë¤.
본 ě°ęľŹěě 1961ë
-2016ë
ę¸°ę° ëěě ě° ěľë ę°ěë ëśíŹě ě íŠëśíŹëĄ ěźë°íë ꡚěšëśíŹ(Generalized Extreme Value Distribution, GEV)ě ëłí ě¤ě íëě¸ Gumbel ëśíŹëĽź ě ě íěë¤. GEV ëśíŹë ěľëěš íšě ěľěěš ëą ęˇšěšěëŁě ë°ěëšë ëśěě ě죟 ě´ěŠë늰 íëĽ ë°ëí¨ěë ë¤ěęłź ę°ë¤(Eq. (1)).
ěŹę¸°ě Îą, β, Ď0ë ěśě˛ë§¤ę°ëłě(scale parameter), íě매ę°ëłě(shape parameter), ěěšë§¤ę°ëłě(location parameter)ëź ëśëĽ´ëŠ° íě매ę°ëłě β=0ěź ë뼟 Type-â
(EV1)ëśíŹ, Gumbel ëśíŹëź íęł ě° ěľë íěë ë° ę°ěë ëšëí´ěě ěźë°ě ěźëĄ ě°ě´ęł ěë¤. ęľë´ěěë íëĽ ę°ěë ě°ě ě Gumbel ëśíŹëĽź ěŹěŠíęł ěěźëŠ° ě¤ęłíěë ě°ě ěěë Gumbel ëśíŹ ěŹěŠě 기ě¤ěźëĄ íęł ěë¤. ë°ëźě 본 ě°ęľŹěěë ě° ěľë ę°ěëě ě íŠëśíŹëĽź Gumbel ëśíŹëĄ ě ě íěěźëŠ° ëśíŹě 매ę°ëłě ěśě ě í본ě íŹę¸°ę° ěěë ěëě ěźëĄ ěíĽě ě ę˛ ë°ěźëŠ° ěëŁě ě´ěěšę° ěë 경ě°ěë ě곥íšěąě´ íŹę˛ ëíëě§ ěë ěĽě ě´ ěë íëĽ ę°ě¤ëިëŠí¸ë˛ě ě ěŠíěë¤. ë¤ěě Gumbel ëśíŹě íëĽ ë°ëí¨ěëĄ ę°ěŠěëŁě ëí ěśě˛ë§¤ę°ëłěě ěěšë§¤ę°ëłě뼟 ě°ě íěŹ ëŻ¸ëě ě° ěľëěš ę°ěëě ëłíě ë°ëĽ¸ 매ę°ëłě ěę´ěąě ëśěíěŹ íëĽ ë°ëí¨ě ëłí뼟 ě ěíęł ě íë¤(Eq. (2)).
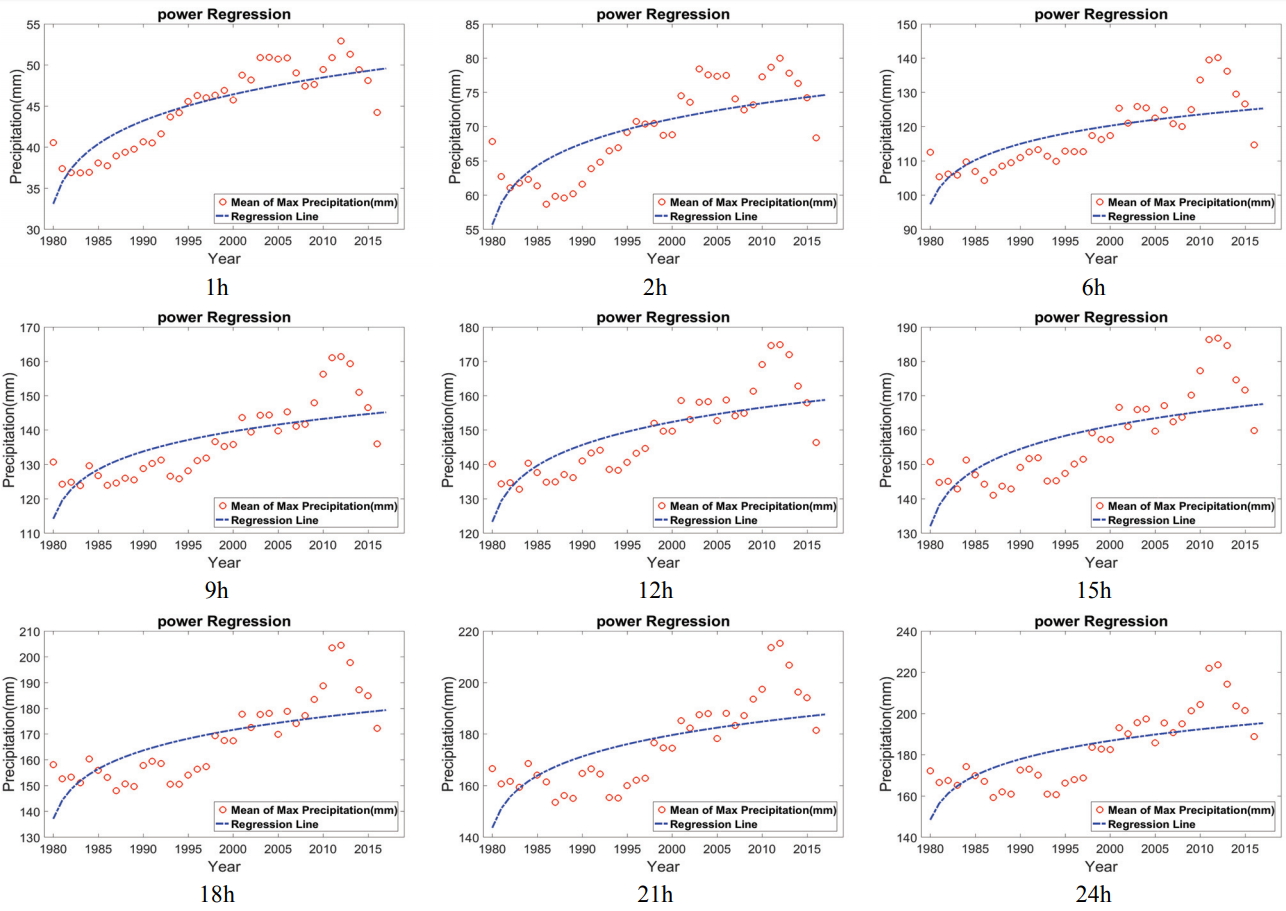
ě° ěľë ę°ěëě ě ííęˇ ëŞ¨íěźëĄ ěśě í ę˛˝ě° ě¸ě˝ę¸°ę° 길ě´ě§ě ë°ëź 돟댏ě ěźëĄ íëšíě§ ěě ë§¤ě° í° ę°ě ě츥íë ë¨ě ě ę°ě§ëŻëĄ ě ííęˇëިíě ě ěŠěë íęłëĽź ę°ě§ë¤. 본 ě°ęľŹěě 돟댏ě ěźëĄ íëšíě§ ěë ę°ě ě¸ě˝ íęłëĽź ꡚ볾í기 ěíěŹ ëłěě ěë ´íšěąě ě¸ě ěźëĄ ě íí ě ěë ëšě í íęˇ ëŞ¨íě¸ Logistic íęˇëިíęłź Power íęˇëިíě ě´ěŠíěŹ ě° ěľë ę°ěëě ě°ě íěë¤.
Logisticíęˇëިíě ë
댽ëłěě ě íę˛°íŠ íëĽ ě ě´ěŠí ě í모íě íšěí 경ě°ëĄě Coxę° 1958ë
ě˛ě ě ěíěë¤. ěźë°ě ě¸ íęˇëިíěě ë
댽ëłěę° â âěě + âě ë˛ě뼟 ę°ě§ëŠ´ ě˘
ěëłě ëí â âěě + âě ë˛ě뼟 ę°ě§ë ę˛ě ë°í´ ë
댽ëłěě ě˘
ěëłě뼟 0-1ěŹě´ě íëĽ ëĄ ę´ęłëĽź ëíë¸ë¤. ëí ë
댽ëłěę° ě˘
ěëłěě 미ěšë ěíĽě ě ë뼟 ëł´ë¤ ě ëě ěźëĄ ííí ě ěë ěĽě ě ę°ě§ęł ěë¤. Logistic í¨ěë ë¤ěęłź ę°ë¤(Eq. (3)).
ěŹę¸°ě δë íęˇęłě, Ďë ë
댽ëłěě´ë¤. 미ëëłíě ëí Logistic íęˇëިí ě ěŠě ěě´ ěŁźěí´ěźí ě ě íšě ę°ěźëĄě ěë ´ěąě´ ëě í¨ěíšěąě ę°ě§ëŻëĄ ëěę°ě 돟댏ě ęą°ëě´ ě´ě ěë°ë ë ě ěŠě 죟ě뼟 ěíë íęłëĽź ę°ě§ë¤.
Power íęˇëިí ëë log-log íęˇëިíě´ëźęł ëśëĽ´ëŠ° ě ííęˇě ëšěˇíë ě˘
ěëłěě ë
댽ëłěě ëĄęˇ¸ ëłíě 졨í í ě ííęˇëśěě ě¤ěíěŹ íęˇęłě뼟 꾏íë¤ë ě ěě ë¤ëĽ´ë¤(Good and Hardin, 2012). ěźë°ě ěźëĄ Power íęˇëިí ëśěě ě ííęˇëśěě 기ě´íěŹ ë
댽ëłěě ě˘
ěëłěě ę´ęłę° ě íě´ě§ ěęą°ë, í ëłě ë´ ěěšě ě°¨ě´ę° 읤ě ě¤ě ě ě íę´ęłëł´ë¤ ë ěë§í ě íę´ęłëĽź ëł´ě´ë 경ě°ě ěŹěŠíë¤. ë¤ěě Power íęˇëިíě ěźë°ěě´ë¤(Eq. (4)).
ěŹę¸°ě íęˇęłě Îą, βë ëłěě ëĄęˇ¸ëĽź 졨í í ě ííęˇëĽź ě¤ěí lny = βlnĎ + Î´ëĄ ě°ě íë¤. 본 ě°ęľŹěě ě˘
ěëłěë 1961ë
-2016ë
ę¸°ę° ëěě ě§ěěę°ëł ě° ěľëę°ěëě´ëŠ° ë
댽ëłěë ę° ě°ë뼟 졨íěë¤. Powerí¨ěě íšěąě 미ë ęą°ëě ëíěŹ ě ě§ě ěźëĄ ěŚę°íë ęą°ëě ě 꾏íí ě ěěźë 미ë ęą°ëě ě¸ě˝íí뼟 ęłźęą° ěëŁě ë°ëź ě í´ě§ë¤. ě ě í Logistic íęˇëިíëżë§ ěëëź ě 체ě ě¸ íęˇëިíě íęłě¸ íęˇëިí ě íě ë°ëź 미ë ęą°ëíí뼟 죟ę´ě ěźëĄ 결ě íę˛ëë íęłëĽź ę°ě§ë¤.
ě¸ęłľě ę˛˝ë§ ëŞ¨íě ëëę° ěěŹę˛°ě ě íë ęłźě ě 모밊íěŹ ę°ë°ë íľęłíě 모íěźëĄ 1943ë
ëě McCulloch and Pittsě ěí´ ě˛ě ě ěëěěźëŠ° íěŹěë ěëŁ, ě í¸ě˛ëŚŹ ëą ë¤ěí ëśěźěě íěŠëęł ěë¤. 본 ě°ęľŹěě ěë댏ě¤ě ë°ëĽ¸ 기í모íě 결곟ę°ě ě´ěŠíěŹ ëŻ¸ë ꡚěšę°ě íšěą ëłíě ěŹěŠëë 몊íě°ë íęˇ ě° ěľë ę°ěëě ëłí뼟 ě츥í기 ěíěŹ ě¸ęłľě ę˛˝ë§ ę¸°ë˛ě ě ěŠíěë¤. ě¸ęłľě 경ë§ě ë¤ě°¨ě ěëŁě ěí¸ę´ęłëĽź ííí ěëŁě˛ëŚŹ 기ë˛ě íëëĄ ë¤ě¸ľě¸ęłľě 경ë§(multi-layer neural network)ě ę˛˝ě° ę¸°ëł¸ě ěźëĄ ě
ë Ľě¸ľ(input layer), ěë츾(hidden layer), ěśë Ľě¸ľ(output layer)ěźëĄ 꾏ěąë늰 ę° ě¸ľě ěŹëŹ ę°ě ë
¸ëëĄ ęľŹěąëęł ę° ě¸ľę°ě ë
¸ëë ě ě´í¨ěě ę°ě¤ěšëĄ ě°ę˛°ëě´ ěë¤. íěľęłźě ě íľíěŹ ě ě´í¨ěě ěľě 매ę°ëłěě ę°ě¤ěšëĽź 결ě íë¤. ě ě´í¨ěë ěźë°ě ěźëĄ Step í¨ě, Sigmoid í¨ě, Relu í¨ě ëąě´ ěë¤. íěľě ě ííęˇě˛ëź ěľěě ęłąë˛ ëąě ěŹěŠíěŹ ę° ë
¸ëë§ë¤ ę°ě¤ěšě ě¤ě°¨ëĽź ě°ě íë¤. 본 ě°ęľŹěě ě
ë Ľě¸ľ ě
ë ĽěëŁë ě°ę°ěë, ě§ěěę°ëł ě° ěľë ę°ěë ëąěźëĄ 꾏ěąíěěźëŠ° ę° ě
ë Ľë
¸ë ę°ě ę°ě¤íŠě´ ěěľě¸Ąě ë
¸ëę°ě íěąíë¤(Eq. (5)).
ěŹę¸°ě, xë ě
ë Ľë
¸ëę°ě ëíë´ëŠ° wjië ě ę˛˝ë§ ę°ě¤ěšě´ëŠ° mě ě
ë Ľë
¸ëě ě´ ę°ě뼟 ëíë´ëŠ° ně ěë츾ě ě´ ë
¸ëě뼟 ëíë¸ë¤. ěë츾 ë
¸ëę°ě ě ě´í¨ěě ě˘
ěëłěëĄ íěŹ ě°ě ë í¨ěę°ě ę°ě¤ěšëĽź ě ěŠí ę°ë¤ě íŠě ěśë Ľę°ěźëĄ íěŹ íěľę¸°ę°ě ëí ě° ěľëěš ę°ěëęłźě ě íŠěąě ę°ě íë íěľęłźě ě ěííěë¤(Eq. (6)).
본 ě°ęľŹěěě ëšě ěě ęł ë ¤í ëšëí´ěě ě ě°¨ë ěě¸ ě§ě ě ëěěźëĄ ę°ěę´ě¸ĄěëŁëĽź ě´ěŠíěŹ ě˛ě 1961ë
-1980ë
ëěě ę° ë
ëëł ěľëę°ěëě íęˇ ě ě°ě íęł ě´í 1ë
ěŠ ëě í늴ě ë
ëëł ěľëę°ěëě íęˇ ě ě°ě í ëě íęˇ ě° ěľë ę°ěëęłź ëěź ę¸°ę° ę°ěěëŁě Gumbel ëśíŹě 매ę°ëłě ęłě°íęł ě ííęˇ ëŞ¨íě 꾏ěśíěë¤. ę´ě¸Ą ěëŁëĽź ë°íěźëĄ ęłě°ë ëě íęˇ ě° ěľë ę°ěë ěëŁëĽź ě´ěŠíěŹ Logistic모íęłź Power모íě íľíěŹ ëŞŠíě°ëě ě§ěěę°ëł ëě íęˇ ě° ěľë ę°ěëě ëšě í íęˇë°Šë˛ěźëĄ ě°ě íěë¤. ëí GCM ěëŁëĽź CM기ë˛ěźëĄ ë¤ě´ě¤ěźěźí í ě츥ë ę°ěě ě§ěěę°ëł ě° ěľë ę°ěëě ęłě°íęł ě´ëĽź ě¸ęłľě 경ë§ě ě
ë ĽěëŁëĄ 몊íě°ëě ě° ěľë ę°ěëě ě°ě íěë¤. ě°ě ë ëě íęˇ ě° ěľë ę°ěëě ě´ěŠíěŹ ëŞŠíě°ëě Gumbel ëśíŹě 매ę°ëłě뼟 ěśě íęł íëĽ ę°ěëě ě°ě íěë¤. ěŹěŠë ě§ěěę°ě 1, 12, 24ěę°ě´ëŠ° 몊íě°ëë 2050, 2080, 2100ë
ěźëĄ ě ě íěë¤. ëě íęˇ ě° ěľë ę°ěëě CMAMP(Cumulative Mean Annual Maximum Precipitation)ëźíęł ě´í CMAMPëĄ íííë¤.
ě§ěěę°ëł ě° ěľëěš ěëŁě ëí Gumbel ëśíŹě 매ę°ëłě ěśě ě ěíěŹ ę´ě¸Ąę¸°ę° 1961ë
-2016ë
ěě ě˛ěě 1961ë
-1980ë
ě ëěě 매ę°ëłě뼟 ěśě íęł 1ë
ěŠ ëě í늴ě ěěšë§¤ę°ëłěě ěśě˛ë§¤ę°ëłě뼟 ěśě íěŹ ë§¤ę°ëłě ëłëęłź ëě íęˇ ě° ěľë ę°ěëě ěę´ę´ęłëĽź ëśěíěë¤. Fig. 2ë ě§ěěę° 24ěę°ě ëí ëě íęˇ ě° ěľëěš ëłíě ë°ëĽ¸ ěěšë§¤ę°ëłěě ěśě˛ë§¤ę°ëłěě ěę´ę´ęłëĽź ëíë¸ë¤. 본 ě°ęľŹěěë ę´ě¸ĄěëŁě 기ë°íěŹ ęˇšěšëśíŹíě 매ę°ëłě ëłíę° ě§ěěę°ëł ëě íęˇ ě° ěľëěš ěëŁě ëłíě ë°ëĽ¸ ěę´ěąě 기ë°íěŹ ě§ěěę°ëł 미ë ëě íęˇ ě° ěľëěšě ëłíě ě츥ě ë°ëź í´ëš ěëŁě íëĽ ëśíŹíě ëłí뼟 ě츥íęł ě íěěźëŻëĄ ě ě í ë°ě ę°ě´ 몊íě°ëě ëě íęˇ ě° ěľëěš ëšě í ęą°ëě Logistic 모í, Power 모í ë° GCM ěëŁě ě¸ęłľě 경ë§ě ě°ęłí ě츥ě íľíěŹ ëšęľëśěíěë¤.
ę´ě¸ĄěźëĄëśí° ě°ě ë CMAMP뼟 ě´ěŠíěŹ Logistic íęˇëިíě ě´ěŠíěŹ ëŞŠíě°ëëł CMAMP뼟 ě°ě íěë¤. Fig. 3ě Logistic íęˇëިíě ě´ěŠí 결곟ě´ëŠ° ëëśëśě ě§ěěę°ě ëíěŹ CMAMP ęą°ëě´ Logistic íęˇęłĄě ě ě ë°ëĽ´ë ę˛ěźëĄ ëíëŹë¤. ě íŠë íę°ëĽź ěíěŹ 1980ë
-2016ë
ę¸°ę° ëě Logistic íęˇëިíě ě§ěěę°ëł íľęłę˛ě 결곟 결ě ęłěë ě˝ 0.78-0.85ëĄ ëíëŹěźëŠ° 몊íě°ëëł CMAMPë ë¤ěęłź ę°ë¤(Table 1).
Logistic 기ë˛ě ë
댽ëłěě ě˘
ěëłě뼟 0-1ěŹě´ě íëĽ ëĄ ę´ęłëĽź ëíë기 ë돸ě ěśě 기ę°ě´ 길ě´ě§ěëĄ íšě ę°ěźëĄ ěë ´íë¤ë ë¨ě ě´ ěë¤. ě´ëŹí ë°Šë˛ëĄ ě íęłë Table 1 결곟ěě íě¸ëëŻě´ ě§ěěę° 2, 6, 18, 24ěę° ëąěě 몊íě°ë 2050ë
ęłź 2080ë
ěěë CMAMPěę° ěŚę°íë 2080ë
ęłź 2100ë
ěěë ě°¨ě´ę° ěěźëŠ° ë¤ëĽ¸ ě§ěěę°ěěë CMAMPě ě°¨ě´ë 미미íë¤.
ě ě í Logistic íęˇëިíęłź ę°ě´ ę´ě¸ĄěźëĄëśí° ě°ě ë CMAMP뼟 ě´ěŠíěŹ Power íęˇëިíě ě´ěŠíěŹ ëŞŠíě°ëëł CMAMP뼟 ě°ě íěë¤. Fig. 4ë Power íęˇëިíě ě´ěŠí 결곟ě´ëŠ° ě íŠë íę°ëĽź ěí Logistic íęˇëިíęłź ëšęľę˛°ęłź ě§ěěę°ě ëíěŹ CMAMP ęą°ëě´ Logistic íęˇęłĄě ě ëší´ ě íŠëę° ëŽę˛ íę°ëěë¤. 1980ë
-2016ë
기ę°ëě Power íęˇëިíě ě§ěěę°ëł íľęłę˛ě 결곟 결ě ęłěë ě˝ 0.55-0.7ëĄ ëíëŹěźëŠ° 몊íě°ëëł CMAMPë ë¤ěęłź ę°ë¤(Table 2). Power 기ë˛ě ěśě 기ę°ě´ 길ě´ě§ěëĄ ěë ´íë Logistic 기ë˛ě ë¨ě ě ëł´ěí ě ěë¤. ꡸ëŹë Table 2 결곟ěě íě¸ëëŻě´ ě§ěěę° ě 체ě ëíěŹ ě íŠëę° Logistic 모íëł´ë¤ ëŽěźëŠ° 몊íě°ëę° ę¸¸ě´ě§ěëĄ íęˇę° ëí ěŚę°íë ęą°ëě ę°ě íë¤ë ë¨ě ě ę°ě§ë¤.
ě¸ęłľě ę˛˝ë§ ëŞ¨íě ě´ěŠíěŹ ëŞŠíě°ëě CMAMP뼟 ě°ě í기 ěíěŹ ë¤ěęłź ę°ě´ ě¸ęłľě ę˛˝ë§ ëŞ¨íě 꾏ěśíěë¤. ěë츾ě ë
¸ëë RCP ěë댏ě¤ëł, ě§ěěę°ëłëĄ 10ę°ěě 30ę° ěŹě´ëĄ 꾏ěąíěěźëŠ° íěľęłźě ě Levenberg-Marquardt backpropagation algorithmě ě´ěŠíěë¤. ě
ë Ľëłěë ě°ę°ěë, ě´ëíęˇ ěźëĄ 꾏í ě§ěěę°ëł ě° ěľë ę°ěë 9ę°, Block maxima ë°Šë˛ěźëĄ 꾏í ě§ěěę°ëł ě° ěľë ę°ěë 9ę°ëĄ ě´ 19ę°ëĄ 꾏ěąíěěźëŠ° ěśë Ľëłěë CMAMP 1ę°ě´ë¤. ě¸ęłľě ę˛˝ë§ íë ¨ě ěíěŹ ěëŁě 70%뼟 ě´ěŠíěěźëŠ° ę˛ě ęłźě ěë 30%ě ěëŁëĽź ěŹěŠíěë¤. ę° ě§ěěę°ě ëí íë ¨ě íěěźëŠ° RCP 2.6, 4.5, 6.0, 8.5ě ë°ëźě ę°ę° íěľęłźě ě ěííěë¤. ę˛ě íľęłëě MSE(Mean Square Error), R2 ë ę°ě§ëĄ íę°íěěźëŠ° ëśě결곟 RCP 2.6ě ě§ěěę° 1ěę° CMAMPě RCP 8.5ě ě§ěěę° 1ěę° ë° 24ěę°ě ě ě¸í 결ě ęłěę° íęˇ 0.7-0.85ě ę°ě ëł´ěŹ ě¸ęłľě 경ë§ěźëĄ ě°ě ë ě츥ę°ě´ ě ë°ě ěźëĄ ě íŠíë¤ęł íë¨ëěë¤(Table 3).
몊íě°ëëłëĄ ěśě ë CMAMP ę°ě Table 4ěě ě ěíěë¤. ëě íęˇ ě° ěľë ę°ěë íęˇ ëŞ¨íě 꾏ěśíęł ě íŠë ëśě 결곟 Logistic íęˇëިíě ě íŠëę° Power íęˇëިí ëł´ë¤ MSE, R2ěě ë ě°ěí ę˛ě ëě ëł´ěěěë ëśęľŹíęł ëŻ¸ëě ꡚěšęą°ëě´ íšě ę°ě ě ěíę˛ ěë ´í¨ěźëĄ 미ë ëłí뼟 결ě íë¤ë íęłëĽź ę°ě§ë¤. GCM ěëŁě ě°ęłíěŹ ëŞŠíě°ë CMAMP ě츥ě RCP 8.5 ě ě¸í ěë댏ě¤ěě ěëě ěźëĄ ëŽě ę°ě ě츥íěë¤.
ě ě í Logistic모íęłź Power모í, ě¸ęłľě ę˛˝ë§ ëŞ¨íěźëĄ ěě°ë 몊íě°ëëł CMAMP뼟 ě´ěŠíěŹ CMAMPě Gumbel 매ę°ëłěě ě ííęˇëĽź íľíěŹ ëŞŠíě°ëëł Gumbelě ěěš, ěśě 매ę°ëłě뼟 ěśě íěë¤(Table 5). ě ěěąě ę°ě í 몊íě°ëëł ę°ě ě§ěěę°ě ë°ëĽ¸ íëĽ ę°ěëě ěŹíę¸°ę° 100ë
ęšě§ ě°ě íęł ëšě í íęˇëިíě íľí´ ěśě ë Gumbel ëśíŹě 매ę°ëłě뼟 ě´ěŠíěŹ ëŞŠíě°ëëł ę°ěě§ěěę°ě ë°ëĽ¸ íëĽ ę°ěëě ě°ě íěë¤(Fig. 5). Fig. 5ěě Së 1961ë
-2016ë
ę¸°ę° ëěě ěëŁëĽź ě´ěŠí ě ěěąě ę°ě í íëĽ ę°ěëě´ëŠ° Lě Logistic íęˇëśěě íľí íëĽ ę°ěë, Pë Power 모íě ě´ěŠí íëĽ ę°ěë, C2, C4, C6, C8ě CM기ë˛ěźëĄ ë¤ě´ě¤ěźěźí RCP ěëëŚŹě¤ 2.6, 4.5, 6.0, 8.5 ěëŁëĽź ě¸ęłľě 경ë§ě íľí´ ěě°ë íëĽ ę°ěëě´ë¤. Logistic모íęłź Power모íě ěŹěŠíěŹ ě°ě ë ę°ěëě ě ěěąě ę°ě í íëĽ ę°ěëëł´ë¤ ëëśëśě 몊íě°ë, ě§ěěę°ëł íëĽ ę°ěëěě ëę˛ ě°ě ëěë¤. GCM ěëŁëĽź ěŹěŠíěŹ ě¸ęłľě ę˛˝ë§ ëŞ¨íě íľí´ ě°ě ë íëĽ ę°ěëěěë 모ě 결곟ě ě쥴íëŻëĄ RCP 2.6, RCP 4.5 ěëëŚŹě¤ ę°ěěě ě ěěąě ę°ě í íëĽ ę°ěëëł´ë¤ ëŽę˛ ě츥íë 꾏ę°ë ë°ěíěë¤.
몊íě°ë 2050ë
ë íëĽ ę°ěë ëśěěě RCP 8.5뼟 ě´ěŠí 모íěźëĄ ě°ě ë íëĽ ę°ěëě´ ę°ěĽ ëę˛ ëěěźëŠ° Power모í, Logistic모íě ě´ěŠí ěěëĄ íëĽ ę°ěëě´ ëěë¤. ě§ěěę° 1ěę°ě ě ě¸í 모ë ě§ěěę°ěě ě ěěąě ę°ě í íëĽ ę°ěë ëł´ë¤ ëę˛ ëěźë RCP 2.6ęłź RCP 4.5ěěë ě§ěěę° 12ěę°, ě§ěěę° 24ěę° ę°ěěěë ě ěěą ëł´ë¤ ëŽę˛ ëěë¤. Logistic 모íě ę˛˝ě° ě§ěěę° 1ěę°ěěë ě ěěą ëëš ě˝ 1.2% ę°ěíěěźë ě§ěěę° 12ěę°, 24ěę° ę°ěěěë ě˝ 14-20% ěŚę°íěěźëŠ° Power 모í ëí Logistic 모íęłź ě ěŹí 결곟뼟 ëł´ěěźë 몊íě°ëę° ëě´ë¨ě ë°ëź Logistic모íëł´ë¤ ë í° ěŚę°íě ëł´ěë¤. ě¸ęłľě 경ë§ě ě´ěŠí íëĽ ę°ěë ě°ě ěěë RCP 2.4, RCP 4.5ěěë ě˝ 3% ę°ě, RCP 6.0, RCP 8.5 ěë댏ě¤ěě ě˝ ě ěěą ëëš 5-15% ěŚę°íěë¤. 몊íě°ë 2080ë
ëě íëĽ ę°ěë ëśěěěë ě§ěěę° 1ěę°ě ěŚę°ëĽ ě´ ë¤ëĽ¸ ě§ěěę°ëł íëĽ ę°ěë ëł´ë¤ ëŽě ěŚę°ě¨ ëë ę°ě뼟 ëł´ěë¤. Logistic 모íěěë ě˝ 1% ę°ěíë ę˛ěźëĄ ëíëŹěźëŠ° Power모íěě ě˝ ě ěěą ëëš 2% ěŚę°ě¨ě ëł´ěë¤. ě¸ęłľě ę˛˝ë§ ëŞ¨íěěë RCP 8.5뼟 ěŹěŠí íëĽ ę°ěëě´ ě˝ 5-18% ěŚę°ëĽź ëł´ěŹ ę°ěĽ ëě ěŚę°ě¨ě ëł´ěěźëŠ° RCP 6.5ěěë ě˝ 5%ě ěŚę°ě¨ě ëł´ěěźëŠ° RCP 2.6, RCP 4.5ěěë íë
ęłź ëšěˇí ěě¤ě ëł´ěë¤. 2100ë
ëěě ě°ě ë íëĽ ę°ěë ëśěěěë RCP 8.5ěě ě°ě ë íëĽ ę°ěëě´ ę°ěĽ ëę˛ ěŚę°ě¨ě ëł´ě´ëŠ° 2080ë
ëě ě ěŹí ęą°ëě ëł´ěë¤.
몊íě°ëëł ě§ěěę°ě ë°ëĽ¸ IDF곥ě ě ëśěí 결곟 Logistic, Power 모íě 몊íě°ë 2050ë
ě ě§ěěę° 24ěę°, 몊íě°ë 2100ë
ě ě§ěěę° 24ěę° ëą íëĽ ę°ěë ě°ě ěě 95% ě 뢰꾏ę°ě ë˛ě´ëë 결곟뼟 ëł´ěěźëŠ° RCP 8.5 ěë댏ě¤ëĽź ěŹěŠí ě¸ęłľě ę˛˝ë§ ëŞ¨íě ě§ěěę° 1ěę° íëĽ ę°ěë ě°ě ěě ě 뢰꾏ę°ě ë˛ě´ëë 결곟뼟 ëł´ěë¤. 모ë 몊íě°ëě ě§ěěę° 1ěę° íëĽ ę°ěëě Logistic모íěěë ę°ě뼟 Power모íěěë ě ěěą ëëš ě˝ 1-1.5% ěŚę°íë ę˛ě´ íě¸ ëěěźë ě¸ęłľě ę˛˝ë§ ëŞ¨íě íľí´ ě°ě ë íëĽ ę°ěëě RCP 2.6, 4.5 ěë댏ě¤ěě ě§ěěę°ęłź ěę´ěě´ ę°ě뼟 ëł´ěěźëŠ° RCP 6.0, 8.5ěěë ě˝ 5-20%ě ę°ěëě´ ěŚę°íë ę˛ěźëĄ ëíëŹë¤. Logistic 모íęłź Power 모í, ě¸ęłľě ę˛˝ë§ ëŞ¨í 모ë ęł ë ¤íë ę°ě ě§ěěę°ě´ 길ě´ě§ě ë°ëź ě ěěą ëëš íëĽ ę°ěëě ěŚę°ě¨ě´ ěŚę°íë ę˛ěźëĄ ëíëŹë¤. ꡸ëŹë Logistic 모íě 몊íě°ëę° ëě´ë¨ě ë°ëź ě ěěą ëëš ę˛Šě°¨ę° ě˘ěě§ë 모ěľě ëł´ěěźëŠ° Power모íě ěŚę°íě´ ë 읤ě§ë 모ěľě ëł´ěë¤(Table 6).
본 ě°ęľŹěěë 1961ë
-2016ë
ę¸°ę° ëěě ě§ěěę°ëł ëě íęˇ ě° ěľë ę°ěëě 꾏íęł ëŞŠíě°ëě ëě íęˇ ě° ěľë ę°ěëě ě°ě í기 ěí´ Logistic íęˇëިí, Power íęˇëިíě 꾏ěśíěë¤. ëí GCM ěëŁě ě°ęłí ě¸ęłľě ę˛˝ë§ ëŞ¨íě ě´ěŠíěŹ 1961ë
-2016ë
ëěě ëě íęˇ ě° ěľë ę°ěëě íë ¨íěŹ ëŞŠíě°ëě ëě íęˇ ě° ę°ěëě ěśě íěë¤. ę´ě¸ĄěëŁëĄëśí° ëě íęˇ ě° ěľë ę°ěëęłź Gumbel ëśíŹě ěěš, ěśě 매ę°ëłěě ě íę´ęłëĽź ě´ěŠíěŹ ëŞŠíě°ëě Gumbel ëśíŹě 매ę°ëłě뼟 ěśě íęł ě´ëĽź ě´ěŠíěŹ ě§ěěę°ëł, ěëě¤ëŚŹëł íëĽ ę°ěëě ě°ě íěë¤. 모íěźëĄëśí° ě°ě ë íëĽ ę°ěë ëśěě ěíěŹ ě ěěąě ę°ě í íëĽ ę°ěëęłź ëšęľ ëśěíěë¤. 본 ě°ęľŹě 죟ě ě°ęľŹ 결곟ë ë¤ěęłź ę°ë¤.
ëě íęˇ ě° ěľë ę°ěë íęˇ ëŞ¨í꾏ěśíęł ě íŠë ëśě 결곟 Logistic íęˇëިíě ě íŠëę° Power íęˇëިí ëł´ë¤ MSE, R2ěě ë ě°ěí ę˛ě ëě ëł´ěěźë 기ë˛ě íšěąě 미ë ęˇšěš ęą°ëě ě ěíę˛ íšě ę°ě ěë ´íę˛ íë ë¨ě ě ę°ě§ë¤. GCM ěëŁě ě°ęłí ě¸ęłľě ę˛˝ë§ ëŞ¨íě 몊íě°ë ëě íęˇ ě° ěľë ę°ěëě RCP 8.5 ěë댏ě¤ëĽź ě ě¸íęł ë ěëě ěźëĄ ëŽę˛ ě츥íěë¤. 몊íě°ëëł ëśěěěë 2050ë
Logistic 모íě ę˛˝ě° ě ěěą ëëš ě˝ 15-25% ěŚę°íěěźëŠ° Power 모í ëí ëšěˇí 결곟뼟 ëł´ěë¤. ě¸ęłľě ę˛˝ë§ ëŞ¨íě 모ë RCP 2.6, 4.5 ěë댏ě¤ěěë ě ěěą ëëš ę°ě뼟 RCP 6.0, 8.5ěěë ěŚę°íěë¤. 몊íě°ë 2080ë
ëě íëĽ ę°ěë ëśěěěë Logistic 모íęłź Power모íěě ě ěěą ëëš ě˝ 15-25%ě ěŚę°ě¨ě ëł´ěěźëŠ° Power모íě ě´ěŠí íëĽ ę°ěëě´ Logistic íęˇëިíëł´ë¤ ëě ěŚę°ě¨ě ëł´ěë¤. ě¸ęłľě ę˛˝ë§ ëŞ¨íěěë RCP 8.5뼟 ěŹěŠí íëĽ ę°ěëě´ 7% ěŚę°ëĽź ëł´ěěźëŠ° ěë댏ě¤ëł ěŚę°ě¨ěě ę°ěĽ ëě ěŚę°ě¨ě ëíëë¤. 2100ë
ëěě ě°ě ë íëĽ ę°ěë ëśěěěë RCP 8.5, Power, Logistic 모íěěźëĄ ě°ě ë íëĽ ę°ěëě ěŚę°ě¨ě´ ëę˛ ëíëŹë¤. ě§ěěę°ě ë°ëĽ¸ ě ěěą ëëš íëĽ ę°ěëě ěŚę°ëĽ ëśěěěë 모ë 몊íě°ëěě ě§ěěę° 24ěę° íëĽ ę°ěëě´ ę°ěĽ í° ěŚę°íě ëł´ěěźë RCP 2.6, 4.5ěěë ę°ěíë 모ěľě ëł´ěë¤. Logistic모íě ě§ěěę° 1ěę° íëĽ ę°ěëě´ ę°ěíë 모ěľě ëł´ěěźë ě§ěěę°ě´ ëě´ë¨ě ë°ëź íëĽ ę°ěëě´ ě ěěą ëëš ěŚę°íë ę˛ěźëĄ ëíëŹěźëŠ° Power모íěěë ě ěěą ëëš ě§ěěę° 1ěę° íëĽ ę°ěëě ě˝ 2-35% ěŚę°, ě§ěěę° 12ěę° ě´ěëśí°ë ě˝ 25% ěŚę°íë ę˛ěźëĄ ëíëŹë¤.
ě ěŠí 기ë˛ě ë°ëź ěě´í 결곟뼟 ëł´ěěźë ꡟ본ě ěźëĄ ëšě ííęˇëިíë¤ě ě ěŠě ęˇšěš ěë ´íšěąě´ ě ěŠ ę¸°ë˛ě ë°ëź ěŹě ě ě í´ě§ë ë¨ě ě´ ěë¤. 본 ě°ęľŹěě ě ěŠí ě¸ęłľě ę˛˝ë§ ę¸°ë˛ęłź GCM ěëŁëĽź ě´ěŠí 몊íě°ëëł, ě§ěěę°ëł íëĽ ę°ěëě ě¨ě¤ę°ě¤ ë°°ěś ěë댏ě¤ě ë°ëĽ¸ GCM 결곟ě ě쥴íë íęłëĽź ę°ě§ë 돟댏모íě 미ë ě츥ěšëĽź ě°ęłí ę˛°ęłźëĄ ě ě í íęˇëިí ě ěŠě ë¨ě ě ëł´ěí ëł´ë¤ ëŹźëŚŹě ěźëĄ íëší íëĽ ę°ěë ěě¸Ąě´ ę°ëĽíë¤ęł íë¨ë늰 본 ě°ęľŹ ě ęˇźë˛ ëí 미ë ěěě ę´ëŚŹëĽź ěí íëĽ ę°ěë ě°ě í댽ě íěŠí ě ěě ę˛ěźëĄ ěŹëŁëë¤.
ę°ěŹě ę¸
본 ě°ęľŹë ęľí ęľíľëś 돟ę´ëŚŹě°ęľŹěŹě
ě ě°ęľŹëšě§ě (17AWMP-B079625-04)ě ěí´ ěíëěěľëë¤.
Fig. 2.
Sample Relationship between Annual Maximum (24hr precipitation) and Location Parameter, Relationship between Annual Maximum (24hr precipitation) and Scale Parameter
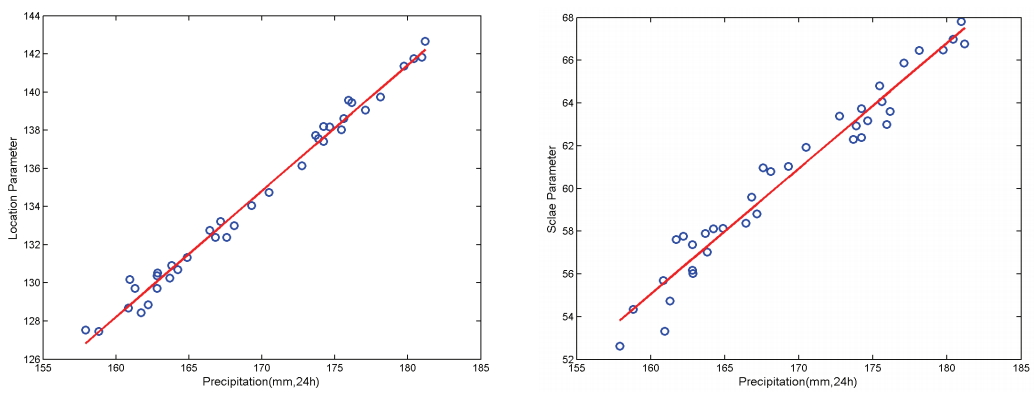
Table 1.
Estimation of the Target Year CMAMP and the Coefficient of Determination using the Logistic Model
Table 2.
Estimation of the Target Year CMAMP and the Coefficient of Determination using the Power Model
Table 3.
Test Statistics for ANN Results
Table 4.
Estimation of the Target Year CMAMP using the ANN Model
Table 5.
Gumbel Parameters of Different Approaches at Target Years
Location parameter
Scale Parameter
Table 6.
Percentage of Change Compared to the Stationary Probable Precipitation
References
KMA (2015). Abnormal Climate Report.
Banach, S. (1922) Sur Les OpĂŠrations Dans Les Ensembles Abstraits Et Leur Application Aux Ăquations IntĂŠgrales. Fundamenta Mathematicae, Vol. 3, pp. 133-181.

Cox, D.R. (1958) The Regression Analysis of Binary Sequences. Journal of the Royal Statistical Society, Series B, Vol. 20, pp. 215-242.


Good, P.I., and Hardin, J.W. (2012). Common Errors in Statistics. John Wiley & Sons.
Hanel, M., and Buishand, T.A. (2010) On the Value of Hourly Precipitation Extremes in Regional Climate Model Simulations. Journal of Hydrology, Vol. 393, pp. 265-273.

He, Y., Brdossy, A., and Brommundt, J. (2006). Non-stationary Flood Frequency Analysis in Southern Germany. Proceedings of The 7th International Conference on Hydro Science and Engineering. Philadelphia, USA.
IPCC (2014). Climate Change 2014: Synthesis Report.
Jang, S.W., Seo, L., Kim, T.W., and Ahn, J.H. (2011) Non-stationary Rainfall Frequency Analysis based on Residual Analysis. Journal of the Korean Society of Civil Engineers, Vol. 31, No. 5B, pp. 449-457 (in Korean).
Kim, G.S., Jo, A.J., Jeon, H.C., and Kim, B.K. (2012). Sensitivity Analysis of Frequency Analysis using Annual Rainfall Exceedance Series. Proceedings of 2012 Annual Conference. Korean Society of Civil Engineers. pp. 805-808 (in Korean).
Kwon, Y.M., and Kim, T.W. (2009) Derived I-D-F Curve in Seoul Using Bivariate Precipitation Frequency Analysis. Journal of the Korean Society of Civil Engineers, Vol. 29, No. 2B, pp. 155-162 (in Korean).
Kwon, Y.M., Park, J.W., and Kim, T.W. (2009) Estimation of Design Rainfalls Considering an Increasing Trend in Rainfall Data. Journal of the Korean Society of Civil Engineers, Vol. 29, No. 2B, pp. 131-139 (in Korean).
Leclerc, M., and Ouarda, T.B.M.J. (2007) Non-stationary Regional Flood Frequency Analysis at Ungauged Sites. Journal of Hydrology, Vol. 343, pp. 254-265.

McCulloch, W.S., and Pitts, W. (1943) A Logical Calculus of the Ideas Immanent in Nervous Activity. The Bulletin of Mathematical Biophysics, Vol. 5, No. 4, pp. 115-133.


Park, Y.J., Kwon, H.-H., Chung, E.S., and Kim, T.-W. (2014) Comparison of Design Rainfalls from the Annual Maximum and the Non-annual Exceedance Series. Journal of the Korean Society of Civil Engineers, Vol. 34, No. 2, pp. 469-478 (in Korean).

Renard, B., Lang, M., and Bois, P. (2006) Statistical Analysis of Extreme Events in a Non-stationary Context Via a Bayesian Framework: Case Study with Peak-over- threshold Data. Stochastic Environmental Research and Risk Assessment, Vol. 21, pp. 97-112.


Shin, H., Nam, W., Jung, Y., and Heo, J. (2008) Uncertainty Assessment of Regional Frequency Analysis for Generalized Logistic Distribution. Journal of the Korean Society of Civil Engineers, Vol. 28, No. 6B, pp. 723-729 (in Korean).
Shin, J.Y., Park, Y.J., and Kim, T.W. (2013) Estimation of Future Design Rainfalls in Administrative Districts Using Nonstationary GEV Model. J. Korean Soc. Hazard Mitig, Vol. 13, No. 3, pp. 147-156 (in Korean).


Sugahara, S., da Rocha, R.P., and Silverira, R. (2009) Non-stationary Frequency Analysis of Extreme Daily Rainfall in Sao Paulo, Brazil. International Journal of Climatology, Vol. 29, pp. 1339-1349.

- TOOLS
-
METRICS

-
- 0 Crossref
- 4,383 View
- 62 Download
- Related articles in KOSHAM
-
Derivation of Probable Rainfall Intensity Formula Using Genetic Algorithm2001 June;1(1)