|
 |
- Search
| J. Korean Soc. Hazard Mitig. > Volume 20(1); 2020 > Article |
|
Abstract
The importance of water quality management in pipes has been recently highlighted through the "Red-water phenomenon" in the city of Incheon. This study proposed a methodology for determining the location of measuring instruments during abnormal water quality issues. The proposed method focuses on analyzing the sensitivity of the flow path through a pipe. Additionally, this flow sensitivity through the tube is analyzed by considering both normal and abnormal conditions. The sensitivity of a pipe is the rate at which the water-flow direction changes. Further, a tube with low sensitivity under normal conditions but high sensitivity under abnormal conditions is the pipe for which the instrument should be first installed. The results were analyzed by applying the proposed methodology to a conventional virtual network. It is expected that, in future, the proposed method for determining the location of water quality gauges could be a useful tool for determining the location of instruments during emergencies.
žöĒžßÄ
žĶúÍ∑ľ žĚłž≤úÍīĎžó≠žčú ž†Āžąėžā¨ŪÉúŽ°ú ÍīÄŽ°ú Žāī žąėžßąÍīÄŽ¶¨žĚė ž§ĎžöĒžĄĪžĚī ŽĆÄŽĎźŽźėÍ≥† žěąŽč§. žĚīŽü¨Ūēú žßÄžÜ枆ĀžĚł žąėžßąŽ¨łž†úžĚė ŽįúžÉĚžĚÄ Ž¨ľ Í≥ĶͳȞčúžä§ŪÖúžóź ŽĆÄŪēú žā¨ŪöĆž†ĀžĚł Ž∂ąžč†žĚĄ žēľÍłį žčúŪā¨ žąė žěąŽč§. Ž≥ł žóįÍĶ¨žóźžĄúŽäĒ ŽĻĄž†ēžÉĀžÉĀŪô© žąėžßą Ž¨łž†úžĚłžßÄŽ•ľ žúĄŪēú Í≥Ąžł°ÍłįžĄ§žĻė žúĄžĻė Í≤įž†ē Žį©Ž≤ēŽ°†žĚĄ ž†úžēąŪēėžėÄŽč§. ž†úžēąŽźú Žį©Ž≤ēžĚÄ ÍīÄŽ°úŽ≥Ą žú†ŪĖ•žĚė ŽĮľÍįźŽŹĄŽ•ľ Ž∂ĄžĄĚŪēėŽäĒ Í≤ɞ̥ ž§Ďžč¨žúľŽ°ú žąėŪĖČŽźúŽč§. ŽĒįŽĚľžĄú ž†ēžÉĀ ŽįŹ ŽĻĄž†ēžÉĀ žÉĀŪô©žĚĄ ÍįÄž†ēŪēėžó¨ ÍīÄŽ°úŽ≥Ą ŽĮľÍįźŽŹĄŽ•ľ Ž∂ĄžĄĚŪēėžėÄžúľŽ©į ÍīÄŽ°úžĚė ŽĮľÍįźŽŹĄŽäĒ Ž¨ľžĚė ŪĚźŽ¶ĄŽį©ŪĖ•žĚī Ž≥ÄŪôĒŪēėŽäĒ ŽĻĄžú®žĚĄ žĚėŽĮłŪēúŽč§. žĶúžĘÖž†ĀžúľŽ°ú ž†ēžÉĀžÉĀŪô©žóźžĄúžĚė ŽĮľÍįźŽŹĄŽäĒ ŽāģžúľŽāė ŽĻĄž†ēžÉĀžÉĀŪô©žóźžĄúžĚė ŽĮľÍįźŽŹĄÍįÄ ŽÜížĚÄ ÍīÄŽ°úŽ•ľ Í≥Ąžł°ÍłįÍįÄ žöįžĄ†ž†ĀžúľŽ°ú žĄ§žĻėŽźėžĖīžēľ ŪēėŽäĒ ÍīÄŽ°úŽ°ú ž†ēžĚėŪēėžėÄŽč§. ž†úžēąŽźú Žį©Ž≤ēŽ°†žĚĄ ŽĆÄŪĎúž†ĀžĚł ÍįÄžÉĀÍīÄŽßĚžóź ž†Āžö©Ūēėžó¨ Í≤įÍ≥ľŽ•ľ Ž∂ĄžĄĚŪēėžėÄžúľŽ©į Ž≥ł žóįÍĶ¨žóźžĄú ž†úžēąŽźú žąėžßąÍ≥Ąžł°Íłį žúĄžĻė Í≤įž†ē Žį©Ž≤ēžĚÄ ŪĖ•ŪõĄ ŽĻĄžÉĀžčúŽ•ľ Í≥†Ž†§Ūēú Í≥Ąžł°Íłį žĄ§žĻė žúĄžĻė Í≤įž†ēžčú žú†žö©Ūēú ŽŹĄÍĶ¨Ž°ú Ūôúžö©Žź† žąė žěąžĚĄ Í≤ÉžúľŽ°ú žėąžÉĀŽźúŽč§.
žĶúÍ∑ľ žĚłž≤úÍīĎžó≠žčú ŽįŹ žĄúžöłŪäĻŽ≥Ąžčúžóź ž†Āžąėžā¨ŪÉúÍįÄ ŽįúžÉĚŪē®žóź ŽĒįŽĚľ žÉĀžąėÍīÄŽß̞󟞥úžĚė žąėžßąÍīÄŽ¶¨ ž§ĎžöĒžĄĪžĚī ŽĆÄŽĎźŽźėÍ≥† žěąŽč§. žÉĀžąėÍīÄŽß̞󟞥úžĚė žßÄžÜ枆ĀžĚł žąėžßąŽ¨łž†úžĚė ŽįúžÉĚžĚÄ žöįŽ¶¨ŽāėŽĚľ Ž¨ľÍīÄŽ¶¨ žčúžä§ŪÖúžĚė žā¨ŪöĆž†Ā Ž∂ąžč†Í≥ľ ŽćĒŽ∂ąžĖī žąėŽŹóŽ¨ľ žĚĆžö©Ž•†žĚė ž†ÄŪēėŽ°ú žĚīžĖīžßą žąė žěąŽč§. žąėŽŹóŽ¨ľŪôćŽ≥īŪėĎžĚėŪöĆžóź ŽĒįŽ•īŽ©ī žöįŽ¶¨ŽāėŽĚľ žąėŽŹóŽ¨ľ žĚĆžö©Ž•†žĚÄ 53.1%Ž°ú Žß§ŽÖĄ ÍįźžÜĆŪēėŽäĒ ž∂ĒžĄłžĚīŽ©į, žĚīžôÄ ÍįôžĚÄ žĚĆžö©Ž•†žĚė ž†ÄŪēėŽäĒ žßĀž†Ďž†Ā/ÍįĄž†Ďž†ĀžĚł žēÖžėĀŪĖ•žúľŽ°ú Žįúž†ĄŽź† žöįŽ†§ÍįÄ žěąŽč§. ŽėźŪēú, Ž¨ľ Í≥ĶÍłČ žčúžä§ŪÖúžĚÄ ŽĆÄÍ∑úŽ™® žā¨ŪöĆÍłįŽįėžčúžĄ§ž§ĎžĚė ŪēėŽāėŽ°úžĄú ŽŹôžčú Žč§Žįúž†Ā žąėžßąŽ¨łž†úÍįÄ ŽįúžÉĚŪē† Í≤Ĺžöį Í∑ł ŪĒľŪēīŽäĒ ŽŹąžúľŽ°úŽäĒ Ž≥ĶÍĶ¨Ūē† žąė žóÜŽäĒ žě¨ŽāúžĚĄ žēľÍłįŪē† žąė žěąžúľŽĮÄŽ°ú, žÉĀžąėÍīÄŽßĚžĚÄ žēąž†Ą ŽįŹ žě¨Žāúžóź žěąžĖīžĄú ž§ĎžöĒŪēėÍ≤Ć ÍīÄŽ¶¨ŽźėžĖīžēľ ŪēėŽäĒ žčúžĄ§Ž¨ľžĚīŽč§.
ÍīÄŽ°ú Žāī žąėžßąŽ¨łž†úžĚė žõźžĚłžĚÄ 1) ŽÖłŪõĄŪôĒ ŽďĪžóź žĚėŪēú ÍīÄ Ž∂ÄžčĚ, 2) ÍīÄŽ°úžį®ŪŹź ŽįŹ ŽįłŽłĆž°įžěĎ, 3) ÍīÄŽßźžßÄž†ź žěĒŽ•ėžóľžÜĆ Ž∂Äž°ĪžúľŽ°ú žĚłŪēú žąėžßąž†ÄŪēė, 4) ÍīÄŽāī ŽĮłžÉĚŽ¨ľ ŽįúžÉĚ žĖĶž†úŽ°ú žĚłŪēú žąėžßąžēÖŪôĒ, 5) ÍīÄŽ°ú žė§ž†ĎžúľŽ°ú žĚłŪēú žė§žóľ ŽďĪ Žß§žöį Žč§žĖĎŪēėŽč§. ŽėźŪēú, ÍīÄŽ°ú Žāī Ž¨ľžĚė ŪĚźŽ¶Ą Žį©ŪĖ•žĚī Ž≥ÄŪôĒŪē®žóź ŽĒįŽĚľ Ūáīž†ĀŽźėžĖī žěąŽćė žĚīŽ¨ľžßąžĚī žĒĽÍ≤® ŪĚėŽü¨ ŽāīŽ†§ÍįÄ ŪÉĀŽŹĄÍįÄ ž¶ĚÍįÄŪēėžó¨ žąėžßąŽ¨łž†úÍįÄ ŽįúžÉĚŪēėŽäĒ Í≤ĹžöįŽŹĄ ŽįúžÉĚŪē† žąė žěąŽč§. ŽĒįŽĚľžĄú žąėžßąŽ¨łž†úžĚė ŽĻ†Ž•ł žĚłžßÄ ŽįŹ žĄ†ž†úž†Ā ŽĆÄžĚϞ̥ žúĄŪēīžĄúŽäĒ ž†Āž†ąŪēú žúĄžĻė ŽįŹ žĖĎžĚė Í≥Ąžł°Íłį žĄ§žĻėÍįÄ ŪēĄžöĒŪēėŽč§. žĶúÍ∑ľ Í≥Ąžł°Íłį žõźÍįÄžĚė ž†ąÍįź ŽįŹ Íłįžą†žĚė Žįúž†ĄžúľŽ°ú žĚłŪēī žÉĀžąėŽŹĄ žčúžä§ŪÖú Žāī Í≥Ąžł°Íłį žĄ§žĻėÍįúžąėÍįÄ Í≥ľÍĪįŽ≥īŽč§ ŪĀ¨Í≤Ć ŪôēŽĆÄŽźėŽäĒ ž∂ĒžĄłžĚīžßÄŽßĆ ÍīÄŽ°ú ŽįŹ žú†žßÄÍīÄŽ¶¨ ŽĻĄžö© ž¶ĚÍįÄ ŽďĪžĚė Ž¨łž†úžóź ŽĒįŽĚľ žöīžėĀÍīÄŽ¶¨žÉĀ žąėžßą žł°ž†ēžĚī ŪēĄžöĒŪēú ž£ľžöĒžßÄž†źžúľŽ°ú žėąžÉĀŽźėŽäĒ žßÄž†źžóź Í≥Ąžł°ÍłįŽ•ľ žĄ§žĻėŪēėÍ≤Ć ŽźėŽ©į ŪēīŽčĻŪēėŽäĒ žúĄžĻėžĚė Í≥Ąžł°Žźú žěźŽ£ĆŽßƞ̥ ÍłįŽįėžúľŽ°ú ÍīÄŽ°ú Žāī žąėžßąžė§žóľž†ēŽŹĄŽ•ľ ž∂Ēž†ēŪēėÍ≥† ÍīÄŽ¶¨ŪēėŽäĒ ŽćįžóźŽäĒ ŽßéžĚÄ ž†úžēĹžĚī žěąŽč§. žĚīžôÄ ÍįôžĚÄ ž†úžēĹž°įÍĪīžĚĄ ŽßĆž°ĪŪēėÍłį žúĄŪēėžó¨ ŪėĄžě¨ÍĻĆžßÄ Žč§žĚĆÍ≥ľ ÍįôžĚÄ žóįÍĶ¨ÍįÄ žĚīŽ£®žĖīž†ł žôĒŽč§. Gueli (2006)žĚÄ Ž¨ľ Í≥ĶÍłČ ÍīÄŽ°ú Žāī žąėžßąžė§žóľžĚė ž°įÍłį ÍįźžßÄŽ•ľ Ž™©ŪĎúŽ°ú Ž©ĒŪÉÄŪúīŽ¶≠žä§ ž†ĎÍ∑ľŽ≤ēžĚĄ Ūôúžö©Ūēī žĶúž†ĀžĚė Í≥Ąžł°Íłį žł°ž†ēžúĄžĻėŽ•ľ žĄ†ž†ēŪēėŽäĒ Žį©Ž≤ēŽ°†žĚĄ ž†úžēąŪēėžėÄžúľŽ©į Propato and Piller (2006)ŽäĒ ŪėľŪē©ž†ēžąėŪĒĄŽ°úÍ∑łŽě®(A Mixed-integer Programming, MIP)Ž•ľ Ūôúžö©Ūēú ÍīÄŽ°ú Žāī žąėžßąžė§žóľ Í≥Ąžł°Íłį žł°ž†ēžúĄžĻė žĄ†ž†ē Žį©žēąžĚĄ ž†úžčú ŽįŹ ž†ēŽüČŪôĒ ŪēėžėÄŽč§. žąėžßąžė§žóľ Í≥Ąžł°Íłį ŽŅź ŽßĆ žēĄŽčąŽĚľ Chung et al. (2009)žĚÄ žóĒŪ䳎°úŪĒľ žĚīŽ°†žĚĄ Ūôúžö©Ūēėžó¨ žÉĀžąėÍīÄŽßĚžĚė Ūö®žú®ž†Ā žöīžėĀžĚĄ žúĄŪēú žĶúž†ĀžĚė žēēŽ†• Í≥Ąžł°žúĄžĻėÍ≤įž†ē Žį©Ž≤ēžĚĄ ž†úžēąŪēėžėÄŽč§. Kessler et al. (1998)žĚÄ EPANET2 (Rossman, 2000) žąėŽ¶¨ŪēīžĄĚžĚĄ ŪÜĶŪēī žú†ŽüČžĚė ŪĚźŽ¶ĄŽį©ŪĖ• Í≥ľ žė§žóľŽ¨ľžßąžĚė žú†žěÖžóź ŽĒįŽ•ł ÍįĀ ž†ąž†źžĚė žė§žóľžó¨Ž∂ÄŽ•ľ Žß§Ū䳎¶≠žä§Ž°ú ÍĶ¨žĄĪŪēėžó¨ žĶúžÜĆŪēúžĚė ÍįźžčúžßÄž†źžúľŽ°ú ÍīÄŽßĚžĚė žąėžßąŽ¨łž†úŽ•ľ ŪÉźžßÄ Ūē† žąė žěąŽäĒ Pollution Matrix Žį©Ž≤ēžĚĄ ž†Āžö©ŪēėžėÄŽč§. žĚī ŪõĄ, Ostfeld and Salomons (2006)ŽäĒ Kessler et al. (1998)žĚė Žį©Ž≤ēžĚĄ Ūôēžě•Ūēėžó¨, Pollution Matrix Žį©Ž≤ēžĚī Žč®žĚľžė§žóľžõźžĚĄ ÍįÄž†ēŪēú Í≤Éžóź ŽįėŪēī Žč§žĖĎŪēú žė§žóľŽ¨ľžßąžĚė žú†žě̥֞ žěĄžĚėŽ°ú ÍįÄž†ēŪēėžó¨ žčúŽāėŽ¶¨žė§ ŪĖČŽ†¨žĚĄ ÍĶ¨žĄĪŪēėŽäĒ RPMŽį©Ž≤ēžĚĄ žÉąŽ°≠Í≤Ć ž†úžčúŪēėÍ≥†, žĶúž†ĀŪôĒ ÍłįŽ≤ēž§Ď ŪēėŽāėžĚł žú†ž†ĄžēĆÍ≥†Ž¶¨ž¶ė(Genetic Algorithm)žĚĄ ž†Āžö©Ūēėžó¨ žĶúž†ĀžĚė žßÄž†źžĚĄ žāįž†ēŪēėžėÄŽč§. žĚī ŪõĄ žÉĀžąėÍīÄŽß̞󟞥úžĚė žąėžßąÍ≥Ąžł°žßÄž†ź žĄ†ž†ēžóź ÍīÄŪēú žóįÍĶ¨ŽäĒ Krause et al. (2006), Watson et al. (2009), Xu et al. (2008, 2010), Tryby et al. (2010), Aral et al. (2010), Cozzolino et al. (2011), Koch and McKenna (2011) ŽďĪžóź žĚėŪēėžó¨ ŪėĄžě¨ÍĻĆžßÄ ŪôúŽįúŪěą žĚīŽ£®žĖīžßÄÍ≥† žěąŽč§. žĄúžöłŪäĻŽ≥Ąžčú žÉĀžąėŽŹĄžā¨žóÖŽ≥łŽ∂ÄžĚė Í≤Ĺžöį žēĄŽ¶¨žąė žąėžßąžěźŽŹôÍįźžčúžčúžä§ŪÖú(Seoul Water Now, SWN)žĚĄ ŪÜĶŪēėžó¨ ŪēúÍįēžĚė žõźžąė, žēĄŽ¶¨žąėžĚė žÉĚžāį ŽįŹ ͳȞąė Í≥ľž†ēžóźžĄú 214ÍįúžĚė ÍįźžčúžßÄž†źžĚĄ žĄ†ž†ēŪēėžó¨ žč§žčúÍįĄžúľŽ°ú žąėžßąžĚĄ žěźŽŹôžł°ž†ē ŽįŹ ÍįźžčúŪēėÍ≥† žěąŽč§. ŪėĄžě¨ÍĻĆžßÄ žßĄŪĖČŽźú žąėžßąžł°ž†ēžßÄž†ź žĄ†ž†ēžóź ŽĆÄŪēú žóįÍĶ¨ŽäĒ Žį©Ž≤ē ÍįĄ žöįžóīžĚė ž†ēŽŹĄŽ•ľ ŪĆźŽč®ŪēėÍłį žĖīŽ†§žöįŽ©į, Í≥Ąžł°Íłį žĄ§žĻėžĚė Ž™©ž†Āžóź ŽĒįŽĚľ Í≤įÍ≥ľÍįÄ Žč¨ŽĚľžßą žąė žěąŽäĒ ŪäĻžĄĪžĚĄ ÍįĖÍ≥† žěąŽč§.
Ž≥ł žóįÍĶ¨žóźžĄúŽäĒ, žąėžßąÍ≥Ąžł°Íłį žúĄžĻė Í≤įž†ēžĚĄ žúĄŪēėžó¨ ÍīÄŽ°ú Žāī ŪĚźŽ¶ĄŽį©ŪĖ•žĚė ŽĮľÍįźŽŹĄŽ•ľ Í≥†Ž†§ŪēėžėÄŽč§. žó¨ÍłįžĄúžĚė ŽĮľÍįźŽŹĄŽěÄ ÍīÄŽ°ú Žāī ŪĚźŽ¶ĄŽį©ŪĖ• Ž≥ÄŪôĒžĚė ž†ēŽŹĄŽ•ľ žĚėŽĮłŪēúŽč§. Žč§žĚĆžúľŽ°úŽäĒ ž†ēžÉĀžÉĀŪô©Í≥ľ ŽĻĄž†ēžÉĀžÉĀŪô© žčúŽāėŽ¶¨žė§Ž•ľ žÉĚžĄĪŪēėÍ≥† ÍīÄžąėŽ°ú žąėŽ¶¨ŪēīžĄĚ ŪĒĄŽ°úÍ∑łŽě® ž§Ď ŪēėŽāėžĚł EPANET2Ž•ľ Ūôúžö©Ūēėžó¨ žčúŽāėŽ¶¨žė§Ž≥Ą ÍīÄŽ°úžĚė ŽĮľÍįźŽŹĄŽ•ľ žāįž†ēŪēėžėÄŽč§. Í≤įÍ≥ľž†ĀžúľŽ°ú ž†ēžÉĀ žÉĀŪô©žĚľ ŽēĆŽäĒ ŽĮľÍįźŪēėžßÄ žēäžēėŽč§ÍįÄ ŽĻĄž†ēžÉĀžÉĀŪô©žĚľ ŽēĆ ŽĮľÍįźŪēīžßÄŽäĒ ÍīÄŽ°úŽ•ľ žąėžßąÍ≥Ąžł°Íłį žĄ§žĻėÍįÄ ŪēĄžöĒŪēú žßÄž†źžúľŽ°ú ž†ēžĚėŪēėžėÄŽč§. Ž≥ł žóįÍĶ¨ Žį©Ž≤ēžĚĄ ŽĎź ÍįÄžßÄžĚė ÍįÄžÉĀÍīÄŽßĚžóź ž†Āžö©ŪēėÍ≥† Í≤įÍ≥ľ Ž∂ĄžĄĚžĚĄ žąėŪĖČŪēėžėÄŽč§.
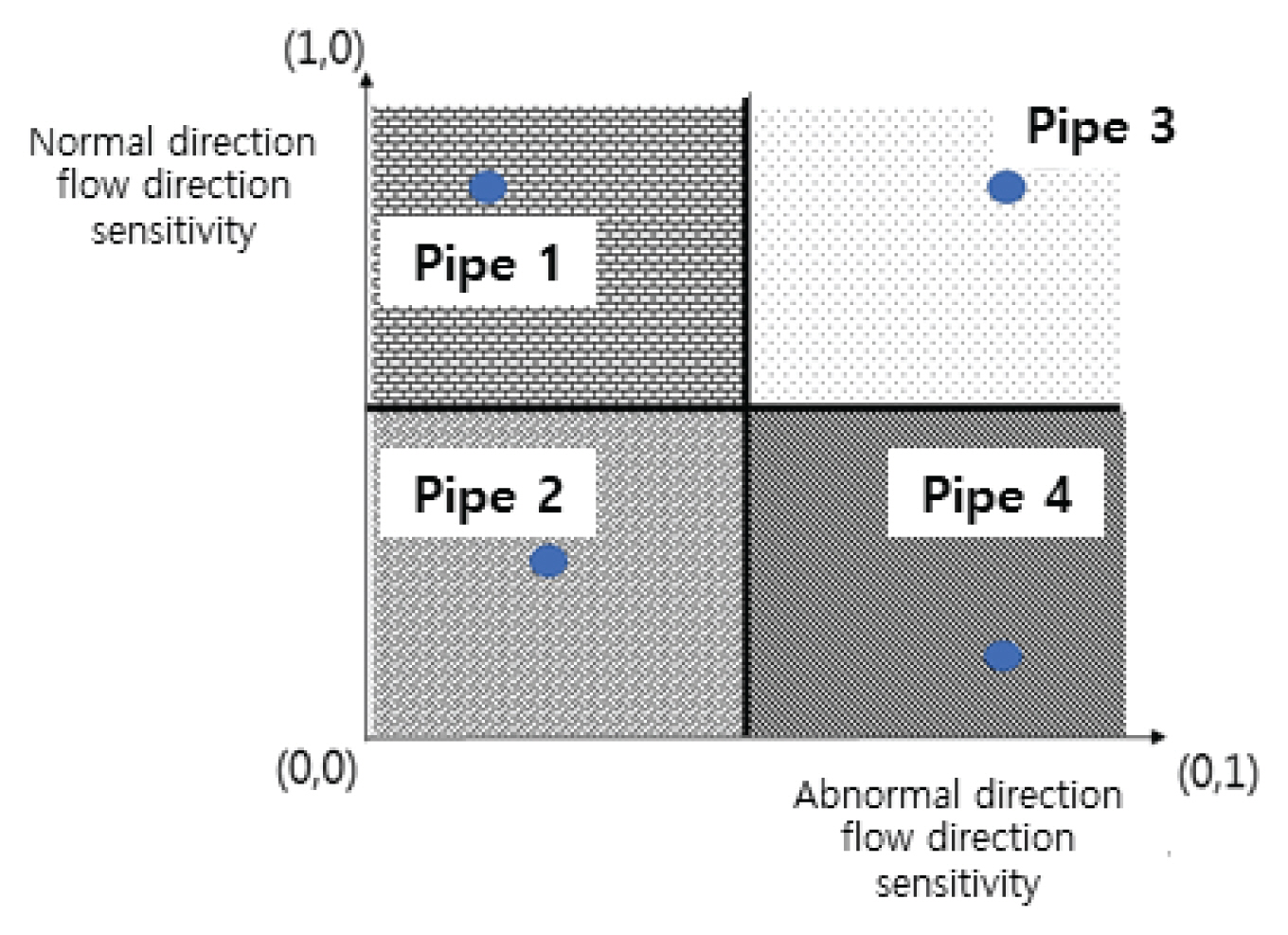
ž†úžēąŽźú žąėžßąÍ≥Ąžł°Íłį žĄ§žĻė žöįžĄ†žßÄžó≠ Í≤įž†ē ž†ąžį®ŽäĒ Fig. 1Í≥ľ ÍįôŽč§. Ž®ľž†Ä, žąėžßąÍ≥Ąžł°Íłį žúĄžĻėÍ≤įž†ēžĚī ŪēĄžöĒŪēú žßÄžó≠žĚė ÍīÄŽßĚž†ēŽ≥ī(žĚľžĚľ žąėžöĒŽüČ ŽįŹ ž†ąž†ź Í≥ľ ÍīÄŽ°úžĚė žúĄžĻė)Ž•ľ ŪöćŽďĚŪēúŽč§. ŽĎź Ž≤ąžßłŽ°úŽäĒ žßĞߥ ŽďĪÍ≥ľ ÍįôžĚÄ ÍīÄŽ°ú ŪĆƞܟžóź žėĀŪĖ•žĚĄ ž§Ą žąė žěąŽäĒ ŽĻĄž†ēžÉĀžÉĀŪô© žčúŽāėŽ¶¨žė§Ž•ľ ÍįÄž†ēŪēúŽč§. Ž≥ł žóįÍĶ¨žóźžĄúŽäĒ ÍīÄŽ°úžĚė žÉĀŪÉúŽ•ľ ‚ÄúClosed‚ÄĚŪēėŽäĒ Í≤ÉžúľŽ°úžĄú ŪĆĆÍīīŽźúŽč§Í≥† ÍįÄž†ēŪēėžėÄŽč§. ŽĒįŽĚľžĄú ÍīÄŽ°úžĚė ÍįúžąėžôÄ ž†ąž†źžĚė žąėžöĒŽüČ ž°įŪē©ŽßĆŪĀľžĚė žčúŽāėŽ¶¨žė§ ÍįúžąėÍįÄ žÉĚžĄĪŽźėÍ≤Ć ŽźúŽč§. žėąŽ•ľ Žď§žĖī, 10ÍįúžĚė ÍīÄŽ°úžôÄ 2ÍįÄžßÄ Ž≤Ąž†ĄžĚė žąėžöĒŽüČžĚī ž°īžě¨ŪēúŽč§Ž©ī ÍįĀ ÍīÄŽ°úŽ•ľ Closed žÉĀŪÉúŽ°ú Ž≥ÄŪôėŪē®žóź ŽĒįŽĚľ žīĚ 10 √ó 2ÍįúžĚė žčúŽāėŽ¶¨žė§ žÉĚžĄĪŽźúŽč§. žĄł Ž≤ąžßłŽ°úŽäĒ žąėŽ¶¨ŪēīžĄĚ ŪĒĄŽ°úÍ∑łŽě®žĚł EPANET2.0žĚĄ Ūôúžö©Ūēėžó¨ ÍįĀ žÉĚžĄĪŽźú žčúŽāėŽ¶¨žė§Ž≥ĄŽ°ú žąėŽ¶¨ŪēīžĄĚžĚĄ žąėŪĖČŪēėÍ≥† žąėžöĒŽüČ ŽĆÄŽĻĄ ÍįĀ ÍīÄŽ°úŽ≥Ą žú†ŪĖ• Ž≥ÄŽŹôžĄĪžĚė ž†ēŽŹĄŽ•ľ žßĀž†ĎžĚłž†ĎŪĖČŽ†¨(Directed Adjacency Matrix)Ž°ú ŪĎúŪėĄŪēúŽč§. Žč§žĚĆžúľŽ°úŽäĒ ÍĶ¨žĄĪŽźú Ž™®Žď† žčúŽāėŽ¶¨žė§Ž≥Ą žßĀž†ĎžĚłž†ĎŪĖČŽ†¨žĚĄ Ūē©žāįŪēėÍ≥† 0Í≥ľ 1žā¨žĚīžĚė ÍįížúľŽ°ú ŪôėžāįŪēėžó¨ ŪėľŪē©žĚłž†ĎŪĖČŽ†¨žĚĄ ÍĶ¨žĄĪŪēúŽč§. žĚīŽēĆžĚė ŪôėžāįžčĚžĚÄ Eq. (1)Í≥ľ ÍįôŽč§.
FPS(i,j) ŽäĒ iž†ąž†źŽ∂ÄŪĄį jž†ąž†ź Žį©ŪĖ•žúľŽ°úžĚė ŪĚźŽ¶Ą ŽĻĄžú® ž¶Č, ÍīÄŽ°úžĚė ŽĮľÍįźŽŹĄŽ•ľ žĚėŽĮłŪēėŽ©į ŪĚźŽ¶ĄžĚī Ūēú Žį©ŪĖ•žúľŽ°ú ŪĚźŽ•łŽč§Ž©ī 0žóź ÍįÄÍĻĆžöī Žč®Žį©ŪĖ•žĄĪÍīĞ̥, ŪĚźŽ¶ĄžĚė Žį©ŪĖ•žĚī žßÄžÜ枆ĀžúľŽ°ú ŽįĒŽÄźŽč§Ž©ī 1žóź ÍįÄÍĻĆžöī ÍįížĚĄ ÍįĖŽäĒ žĖĎŽį©ŪĖ•žĄĪ ÍīĞ̥ žĚėŽĮłŪēėÍ≤Ć ŽźúŽč§. M(i,j)ŽäĒ ž†ąž†ź iŽ∂ÄŪĄį ž†ąž†źjžĚė ŪėľŪē©žĚłž†ĎŪĖČŽ†¨žĚė ÍįížĚĄ žĚėŽĮłŪēėŽ©į i,jŽäĒ ž†ąž†źžĚė Ž≤ąŪėłŽ•ľ žĚėŽĮłŪēúŽč§. ŽßąžßÄŽßČžúľŽ°ú FPS(i,j)ŽäĒ ž†ąž†źÍ≥ľ ž†ąž†źžā¨žĚīžĚė ŽĮľÍįźŽŹĄ(ŽĻĄžú®)žĚīŽĮÄŽ°ú Eq. (2)Ž•ľ Ūôúžö©Ūēėžó¨ žĶúžĘÖž†ĀžĚł ÍīÄŽ°úžĚė žú†ŪĖ•Ž≥ÄŽŹôŽĻĄžú®žĚĄ ÍĶ¨ŪēúŽč§.
žó¨ÍłįžĄú, PS = ÍīÄŽ°úžĚė ŽĮľÍįźŽŹĄ(žú†ŪĖ• Ž≥ÄŽŹô ŽĻĄžú®)žĚĄ žĚėŽĮłŪēėŽ©į Ai,j = ÍīÄŽ°ú IŽ°ú Ž∂ÄŪĄį j ÍīÄŽ°úžĚė žú†ŪĖ• ŽĻĄžú®žĚĄ Ai,j = ÍīÄŽ°ú jŽ°ú Ž∂ÄŪĄį iÍīÄŽ°úžĚė žú†ŪĖ• ŽĻĄžú®žĚĄ žĚėŽĮłŪēúŽč§. Í≤įÍ≥ľž†ĀžúľŽ°ú Fig. 2žôÄ ÍįôžĚÄ Í∑łŽěėŪĒĄŽ•ľ žĖĽžĚĄ žąė žěąŽč§. Í∑łŽěėŪĒĄžÉĀžĚė Pipe 1žĚÄ ž†ēžÉĀžčú ŽĮľÍįźŪēėžßÄŽßĆ ŽĻĄžÉĀžčúŽäĒ ŽĮľÍįźŪēėžßÄ žēäžúľŽ©į Pipe 2ŽäĒ Ž™®Žď† žÉĀŪô©žóźžĄú ŽĮľÍįźŪēėžßÄ žēäžĚÄ ÍīÄŽ°úŽ•ľ žĚėŽĮłŪēúŽč§. Pipe 3žĚė Í≤Ĺžöį Ž™®Žď† Í≤ĹžöįžóźžĄú ŽĮľÍįźŪēú ÍīÄŽ°úŽ°úžĄú Í≥Ąžł°ÍłįÍįÄ žöįžĄ†ž†ĀžúľŽ°ú žĄ§žĻėŽźėžĖī ž†łžēľ ŪēėŽāė Ž≥ł žóįÍĶ¨žĚė ž£ľž†úŽäĒ ŽĻĄžÉĀžčúžĚė Í≥Ąžł°Íłį žúĄžĻė žöįžĄ†žąúžúĄ Í≤įž†ēžĚīŽč§. ŽĒįŽĚľžĄú Ž≥ł žóįÍĶ¨žóźžĄúŽäĒ ž†ēžÉĀžĚľ ŽēĆŽäĒ ŽĮľÍįźŪēėžßÄ žēäžúľŽāė ŽĻĄžÉĀžčúžĚė ŽĮľÍįźŪēú ÍīÄŽ°ú ž¶Č, Pipe 4žóź ŪēīŽčĻŪēėŽäĒ žßÄž†źŽāīžĚė ÍīÄŽ°úŽßƞ̥ Í≥†Ž†§ŪēėžėÄžúľŽ©į Utopian Approach (Xanthopulos et al., 2000)Žį©Ž≤ēžĚĄ ŪÜĶŪēī žöįžĄ†žąúžúĄŽ•ľ Í≤įž†ēŪēėžėÄŽč§. Utopian ApproachŽäĒ ÍĪįŽ¶¨ÍłįŽįė žĚėžā¨Í≤įž†ē ÍłįŽ≤ēžúľŽ°úžĄú ž†ēÍ∑úŪôĒ ŽźėžĖīžěąŽäĒ Í≥ĶÍįĄžóź žĚīžÉĀž†ź(Utopian Approach)Í≥ľžĚė ÍĪįŽ¶¨Ž•ľ ŪÜĶŪēī žöįžĄ†žąúžúĄŽ•ľ Í≤įž†ēŪēėŽäĒ Žį©Ž≤ēžĚīŽč§. Fig. 1žÉĀžĚė 4Ž≤ąÍīÄŽ°ú žßÄž†źžóź ŪēīŽčĻŪēėŽäĒ ÍĶ¨žó≠žóź ŽĆÄŪēú žöįžĄ†žąúžúĄ Í≤įž†ēžĚĄ žúĄŪēėžó¨ (0,1)žĚĄ žĚīžÉĀž†źžúľŽ°ú žßÄž†ēŪēėžėÄžúľŽ©į ÍĪįŽ¶¨ÍįÄ žĶúžÜĆÍįÄ ŽźėŽäĒ žßÄž†źžĚė ÍīÄŽ°úÍįÄ žöįžĄ†ž†ĀžúľŽ°ú Í≥Ąžł°ÍłįÍįÄ žĄ§žĻėŽźėžĖīžēľ Ūē† Í≤ÉžĚīŽč§.
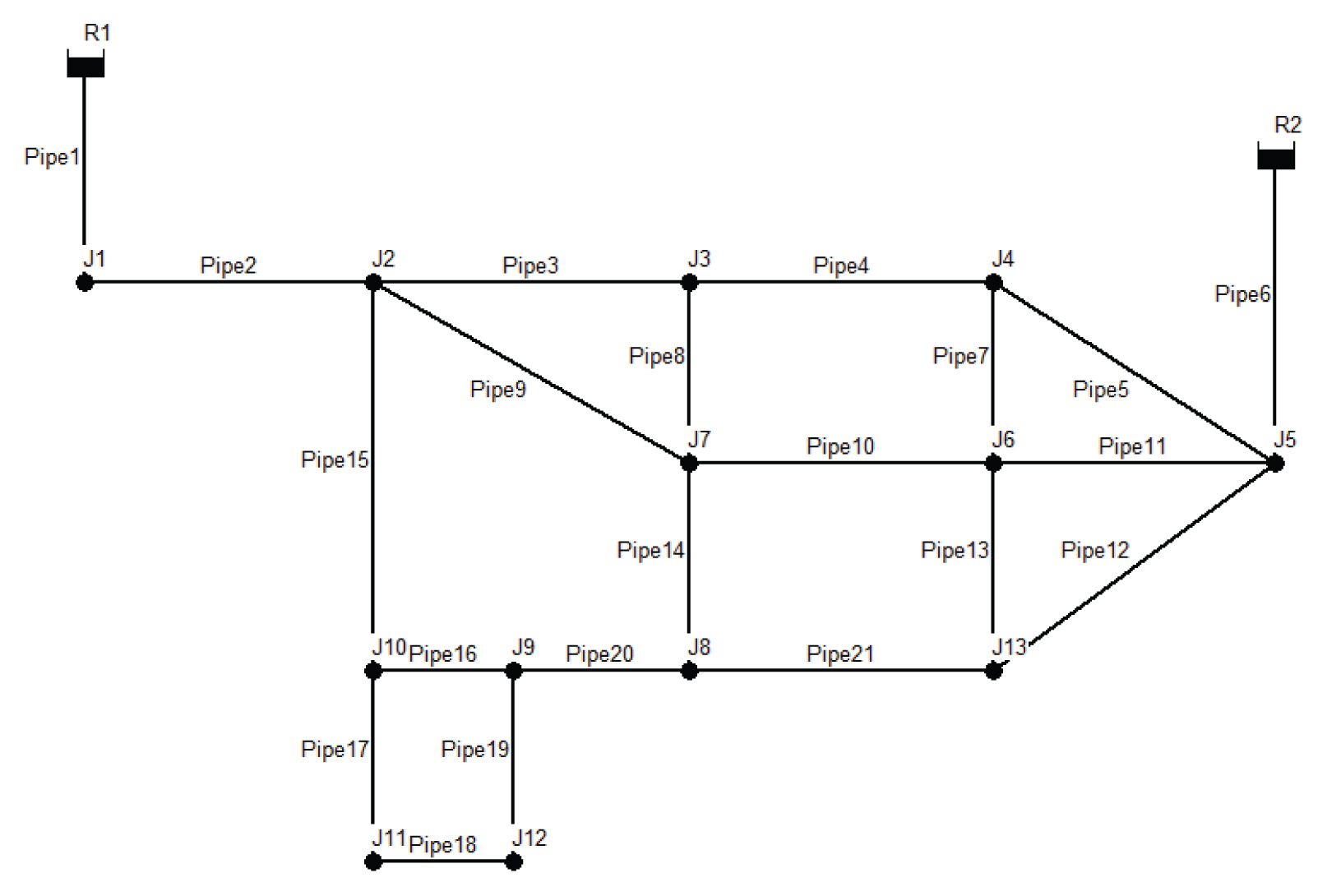
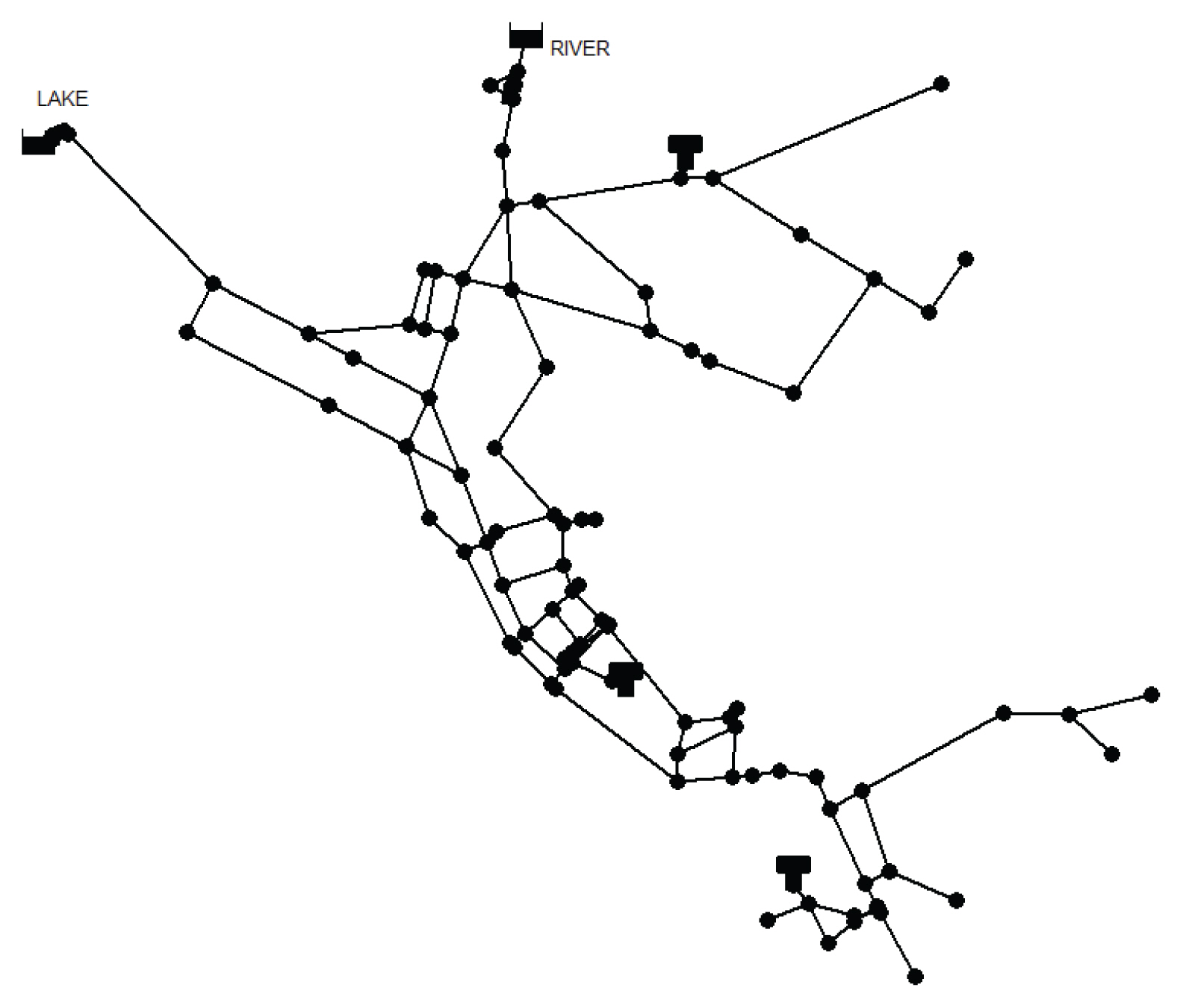
žē장ú ž†úžčúŽźú Žį©Ž≤ēŽ°†žĚĄ Ozger (2003)žóź žĚėŪēī ž†úžčúŽźú ÍįĄŽč®Ūēú ÍįÄžÉĀÍīÄŽßĚ Mays‚Äôs Networks žôÄ EPANET2žĚė žėąž†úÍīÄŽßĚž§Ď ŪēėŽāėžĚł Net3žóź ž†Āžö© ŪēėžėÄŽč§. Mays's NetworksŽäĒ 2ÍįúžĚė žąėžõźžóźžĄú 21ÍįúžĚė ÍīÄŽ°úŽ•ľ ŪÜĶŪēī 13ÍįúžĚė ž†ąž†źžóź 3146CMHŽ•ľ Í≥ĶÍłČŪēėÍ≥† žěąŽäĒ ÍīÄŽßĚžúľŽ°úžĄú ÍĶ¨žĄĪžĚÄ Fig. 3Í≥ľ ÍįôŽč§. Net3žĚÄ ŽĎź ÍįúžĚė žąėžõźÍ≥ľ 92ÍįúžĚė ž†ąž†ź ŽįŹ 117ÍįúžĚė ÍīÄŽ°úŽ°ú žĚīŽ£®žĖīž†ł žěąžúľŽ©į ÍĶ¨žĄĪžĚÄ Fig. 4žôÄ ÍįôŽč§.
Mays's NetworksžĚė žĚľžĚľ žąėžöĒŽüČ Ž≥ÄŽŹôžĄĪžĚĄ žčúÍįĄŽč®žúĄŽ°ú Í≥†Ž†§ŪēėÍłį žúĄŪēī ž≤®ŽĎźŽ∂ÄŪēėžú®žĚĄ Ūôúžö©Ūēėžó¨ 24ÍįúžĚė ž†ąž†źŽ≥Ą žąėžöĒŽüČ ŽćįžĚīŪĄį(Table 1)Ž•ľ žÉĚžĄĪŪēėžėÄŽč§. ME (2008)ŽäĒ ÍĶ≠ŽāīžĚė Í≤Ĺžöį ž≤®ŽĎźŽ∂ÄŪēėžú®žĚė Ž∂ąŪôēžč§žĄĪžĚĄ Í∑ľÍĪįŽ°ú ŪöĆÍ∑ÄŽ™®Žćł ÍįúŽįúžóź žĖīŽ†§žõÄžĚī žěąžĖī 01~05ŽÖĄ žÉĀžąėŽŹĄ ŪÜĶÍ≥Ą žěźŽ£ĆŽ•ľ Ū܆ŽĆÄŽ°ú ž≤®ŽĎźŽ∂ÄŪēėžú®žĚĄ žāįž†ēŪēėžó¨ Table 2žôÄ ÍįôžĚī ž†úžčúŪēėžėÄŽč§.
ÍłįŽ≥łžąėžöĒŽüČ ŽćįžĚīŪĄįŽ•ľ ŪÜĶŪēī ͳȞąėžĚłÍĶ¨ÍįÄ ŽĆÄŽěĶ 2~5ŽßĆŽ™ÖžĚł Í≤ɞ̥ žėąžÉĀŪē† žąė žěąžúľŽ©į ŪēīŽčĻŪēėŽäĒ ž≤®ŽĎźŽ∂ÄŪēėžú® 1.40žĚĄ Ūôúžö©Ūēėžó¨ žąėžöĒŽüČžĚė žīąÍłįÍįí Íłįž§Ä ¬Ī 0.05žĚė ž≤®ŽĎźŽ∂ÄŪēėžú®žĚĄ Í≥ĪŪēėÍ≥† 24ÍįúžĚė ž†ąž†źŽ≥Ą žąėžöĒŽüČ ŽćįžĚīŪĄįŽ•ľ ÍįÄž†ēŪēėžó¨ ŪēėŽ£®(24žčúÍįĄ)ŽŹôžēąžĚė žąėžöĒŽ≥ÄŽŹôžóź ŽĒįŽ•ł žčúŽāėŽ¶¨žė§Ž•ľ žÉĚžĄĪŪēėžėÄŽč§. žē장ú ž†úžčúŽźú Žį©Ž≤ēŽ°†žóź ŽĒįŽĚľ ŽĻĄžÉĀžčúžĚė Í≤ĹžöįŽäĒ ÍīÄŽ°úŽ•ľ ŪēúÍįúžĒ© Closed ŪēėžėÄžúľŽ©į ž†ēžÉĀ žčúŽāėŽ¶¨žė§ŽäĒ ž†ąž†źŽ≥Ą žąėžöĒŽüČŽßƞ̥ Ž≥ÄÍ≤ĹŪēú 24Íįú, ŽĻĄžÉĀžčú žčúŽāėŽ¶¨žė§ 24 √ó 21Íįú žīĚ 528ÍįúžĚė žčúŽāėŽ¶¨žė§žóź ŽĆÄŪēú žąėŽ¶¨ŪēīžĄĚžĚĄ žąėŪĖČŪēėžėÄŽč§.
žē장ú ž†úžčúŽźú Žį©Ž≤ēŽ°†žóź ŽĒįŽĚľ žąėŪĖČŽźú 528ÍįÄžßÄ(ž†ēžÉĀ 24ÍįÄžßÄ, ŽĻĄžÉĀ 528ÍįÄžßÄžĚė žčúŽāėŽ¶¨žė§ ŽĒįŽ•ł žąėŽ¶¨ŪēīžĄĚ Í≤įÍ≥ľŽ•ľ Ū܆ŽĆÄŽ°ú ŪŹČžÉĀ/ŽĻĄžÉĀžčúžóź ŽĒįŽ•ł žßĀž†ĎžĚłž†ĎŪĖČŽ†¨žĚĄ ÍĶ¨žĄĪŪēú Í≤įÍ≥ľ Table 3Í≥ľ ÍįôŽč§. Ž™®Žď† ÍįížĚī 0 ŽėźŽäĒ 1žĚī ŽźėŽ©į Table 3žĚÄ žčúŽāėŽ¶¨žė§ 12Ž≤ąžóź ŪēīŽčĻŪēėŽäĒ ž†ēžÉĀžÉĀŪô©žóźžĄúžĚė žßĀž†ĎžĚłž†ĎŪĖČŽ†¨žĚīŽč§.
žÉĚžĄĪŽźú 528ÍįúžĚė žčúŽāėŽ¶¨žė§Ž≥Ą žāįž†ēŽźú žßĀž†ĎžĚłž†ĎŪĖČŽ†¨žĚĄ Žį©Ž≤ēŽ°†Í≥ľ ÍįôžĚī Ž™®ŽĎź Ūē©žāįŪēėžó¨ ŪēėŽāėžĚė ŪĖČŽ†¨Ž°ú ŪôėžāįŪēėžó¨ žĖĽžĚÄ žĶúžĘÖ ŪėľŪē©žĚłž†ĎŪĖČŽ†¨žĚė Í≤įÍ≥ľŽäĒ Tables 4~5žôÄ ÍįôŽč§. Table 4žĚė Í≤Ĺžöį ž†ēžÉĀžčúŽ•ľ, Table 5žĚė Í≤Ĺžöį ŽĻĄžÉĀžčúžĚė žĶúžĘÖ ŪėľŪē©žĚłž†ĎŪĖČŽ†¨žĚė Í≤įÍ≥ľŽ•ľ žĚėŽĮłŪēúŽč§.
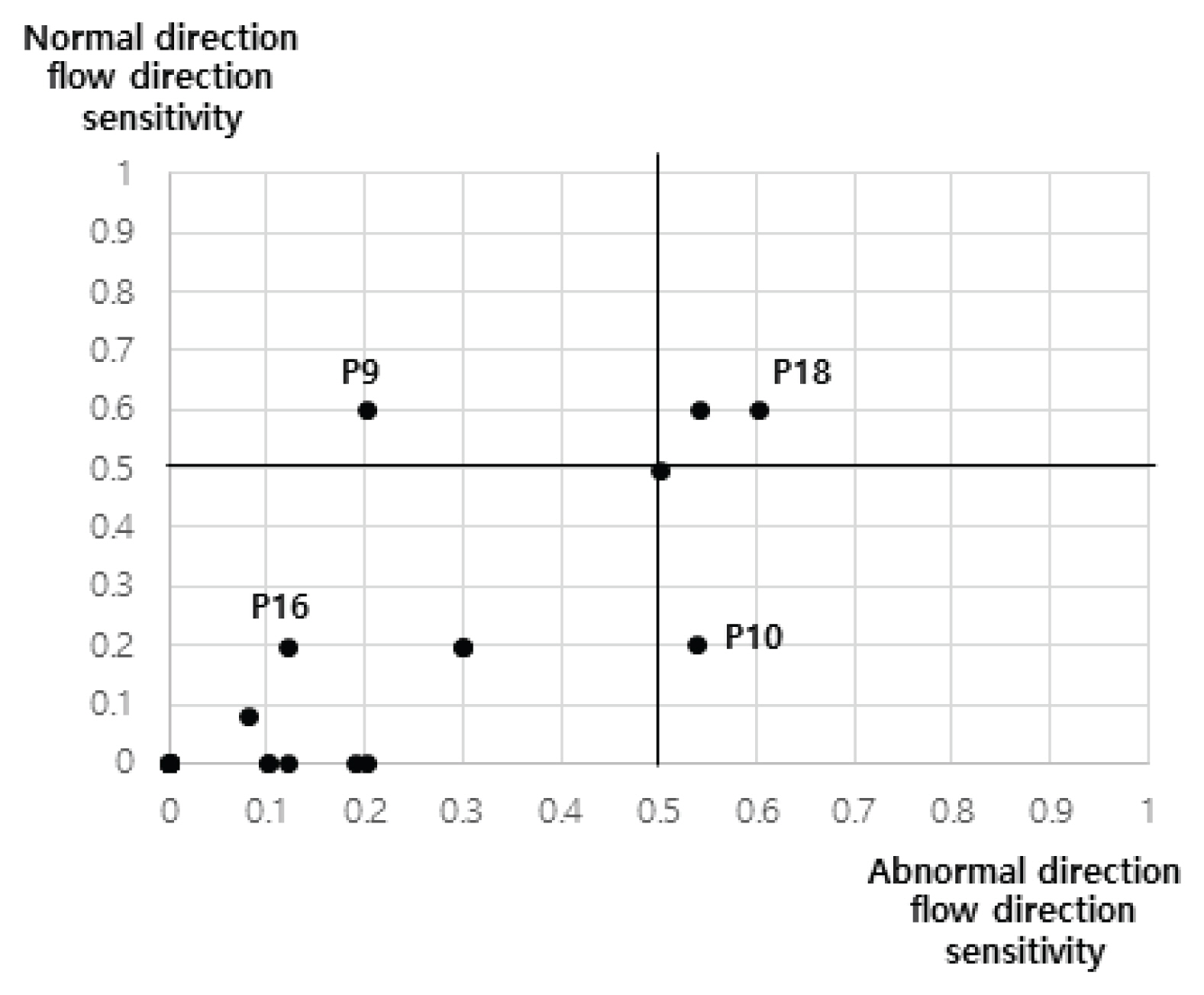
žÉĚžĄĪŽźú ŪėľŪē©žĚłž†ĎŪĖČŽ†¨žĚĄ Eq. (2)Ž•ľ Ūôúžö©Ūēėžó¨ ÍīÄŽ°úžĚė ŽĮľÍįźŽŹĄ(žú†ŪĖ•Ž≥ÄŽŹôŽĻĄžú®)Ž•ľ žāįž†ēŪēú Í≤įÍ≥ľŽ•ľ Table 6Í≥ľ Fig. 5žóź ž†úžčúŪēėžėÄŽč§. ž†úžēąŽźú Žį©Ž≤ēŽ°†žĚĄ ž†Āžö©Ūēú Í≤įÍ≥ľ 10Ž≤ą ÍīÄŽ°úÍįÄ ŽĻĄž†ēžÉĀžčú 0.54, ž†ēžÉĀžčú 0.2žėÄžúľŽ©į (1,0)Í≥ľžĚė ÍĪįŽ¶¨ 0.5žĚė Í≤įÍ≥ľŽ•ľ žĖĽžóąžúľŽ©į, Fig. 4žóźžĄú žó≠žčú 10Ž≤ą ÍīÄŽ°úÍįÄ ž†ēžÉĀžĚľ ŽēĆŽäĒ žú†ŪĖ•žĚė ŽĮľÍįźŽŹĄÍįÄ ŽāģžĚÄ ÍįížĚĄ ÍįĖÍ≥† ŽĻĄžÉĀžčú ŽĮľÍįźŽŹĄÍįÄ ŽÜížēĄ žú†ŪĖ•žĚī Ž≥ÄŪē† ŪôēŽ•†žĚī ŽÜížēĄžßĄ Í≤ɞ̥ ŪôēžĚłŪē† žąė žěąŽč§. ŽĒįŽĚľžĄú Mays's NetworksžóźžĄúŽäĒ 10Ž≤ą ÍīÄŽ°úžóź ŽĻĄžÉĀžčúŽ•ľ ŽĆÄŽĻĄŪēú Í≥Ąžł°ÍłįÍįÄ žöįžĄ†ž†ĀžúľŽ°ú žĄ§žĻėŽźėžĖīžēľ ŪēėŽäĒ Í≤ÉžúľŽ°ú ŽāėŪÉÄŽā¨žúľŽ©į Fig. 6žÉĀžĚė ŽŹôÍ∑łŽĚľŽĮł Ž∂ÄŽ∂Ąžóź ŪēīŽčĻŪēėŽäĒ ÍīÄŽ°úžĚīŽč§.
Net3ÍīÄŽßĚžĚÄ žīĚ 5ÍįÄžßÄ žĚľž†ēŪēú ŪĆ®ŪĄīžĚė žąėžöĒŽüČ Ž≥ÄŽŹô ŽćįžĚīŪĄįÍįÄ žěąŽč§. žĚīŽäĒ EPANETžĚė Extended Period Simulation (EPS) Ž™®žĚėŽ•ľ žúĄŪēú ŽćįžĚīŪĄįŽ°úžĄú žąėžöĒŽüČ Ž≥ÄŽŹôžĄĪžĚĄ žĚľž†ēŪēú ŪĆ®ŪĄīžúľŽ°ú ÍįÄž†ēŪēėÍ≥† žąėŽ¶¨ŪēīžĄĚžĚĄ žąėŪĖČŪēėÍłį žúĄŪēú žěźŽ£ĆžĚīŽč§. ŽĒįŽĚľžĄú Ž≥ł žóįÍĶ¨žóźžĄúŽäĒ Mays's NetworksžôÄ ÍįôžĚī žąėžöĒŽüČŽćįžĚīŪĄįŽ•ľ žÉĚžĄĪŪē† ŪēĄžöĒ žóÜžĚī ŪēīŽčĻ ŽćįžĚīŪĄįŽ•ľ žā¨žö©ŪēėžėÄŽč§. ŪĖ•ŪõĄ žč§ž†úžßÄžó≠žóź ž†Āžö©Ūē† Í≤Ĺžöį žĚľžĚľŽ≥ÄŽŹô žąėžöĒŽüČ ŽćįžĚīŪĄįÍįÄ žěąŽč§Ž©ī ÍįÄž†ēŪē† ŪēĄžöĒÍįÄ žóÜŽč§Í≥† ŪĆźŽč®ŽźúŽč§. NET3žĚė Í≤Ĺžöį ÍīÄŽßĚžĚė ÍĶ¨žĄĪžĚī Mays's NetworksžôÄŽäĒ Žč§Ž•īÍ≤Ć ŽĻĄÍĶźž†Ā Ž≥Ķžě°Ūēėžó¨ ž∂ĒÍįÄž†ĀžúľŽ°ú Í≥†Ž†§Ūē† žā¨Ūē≠žĚī žěąŽč§. žĚľŽ∂Ä ÍīÄŽ°úÍįÄ ŽčęŪěėžóź ŽĒįŽĚľ ÍĶ¨žó≠ ž†Ąž≤īÍįÄ Ž¨ľ Í≥ĶͳȞ̥ ŽįõžßÄ Ž™ĽŪēėŽäĒ žÉĀŪô©žĚī ŽįúžÉĚŪē† žąė žěąžúľŽĮÄŽ°ú Net3ÍīÄŽß̞󟞥úŽäĒ Ž™®Žď† ÍīÄŪĆĆÍīī žčúŽāėŽ¶¨žė§žóź ŽĆÄŪēī žį®ŪŹźžóź ŽĒįŽĚľ ž†ąž†źžóź Ž¨ľ Í≥ĶͳȞĚī Ž∂ąÍįÄŽä•Ūēú žÉĀŪô©žóź žěąžĖīžĄúŽäĒ ŪēīŽčĻ ž†ąž†źžĚė žöĒÍĶ¨žąėžöĒŽüȞ̥ ‚Äú0‚ÄĚžúľŽ°ú žąėž†ēŪēėžó¨ žąėŽ¶¨ŪēīžĄĚžĚĄ žąėŪĖČŪēėžėÄŽč§.
Net3žĚÄ ŽĎź ÍįúžĚė žąėžõźÍ≥ľ 92ÍįúžĚė ž†ąž†ź ŽįŹ 117ÍįúžĚė ÍīÄŽ°úŽ°ú žĚīŽ£®žĖīž†ł žěąŽč§. ŽĒįŽĚľžĄú 24ÍįúžĚė ž†ēžÉĀžčúŽāėŽ¶¨žė§žôÄ 117 √ó 24ÍįúžĚė ŽĻĄžÉĀžčúŽāėŽ¶¨žė§ ž¶Č, žīĚ 2,832ÍįÄžßÄžĚė žÉĚžĄĪŽźú žčúŽāėŽ¶¨žė§žóź Ž≥ł Žį©Ž≤ēŽ°†žĚĄ ž†Āžö©Ūēėžó¨ Table 7Í≥ľ Figs. 7, 8žĚė Í≤įÍ≥ľŽ•ľ žĖĽžĖī ŽāīžóąŽč§. Fig. 7žĚĄ ŪÜĶŪēī žč≠žěźÍįÄ žė§Ž•łž™Ĺ žēĄŽěėŽ∂ÄŽ∂Ąžóź ŪēīŽčĻ(ŽĻĄžÉĀžčú žú†ŪĖ•žĚė ŽĮľÍįźŽŹĄÍįÄ žĽ§žßÄŽäĒ ÍīÄŽ°ú)ŪēėŽäĒ ÍīÄŽ°úŽäĒ žīĚ 7ÍįúŽ°ú Í≤įž†ēŽźėžóąŽč§. Table 7žóźŽäĒ ž†ēŽüČž†ĀžĚł Í≤įÍ≥ľŽ•ľ ž†úžčúŪēėžėÄŽč§. (1,0)Í≥ľžĚė ÍĪįŽ¶¨ÍįÄ 0.7 žĚīŪēėžĚł Ž∂ÄŽ∂ĄžĚĄ Í≥Ąžł°Íłį žöįžĄ†žĄ§žĻė žßÄž†źžúľŽ°ú Í≤įž†ēŪēėžėÄžúľŽ©į žĚīŽ†áÍ≤Ć ÍįÄž†ēŪē† Í≤Ĺžöį 11ÍįúžĚė ÍīÄŽ°úÍįÄ žĄ†ŪÉĚŽźėžóąŽč§. 1žąúžúĄŽäĒ P285Ž°ú Í≤įž†ē ŽźėžóąžúľŽ©į Fig. 8Í≥ľ ÍįôžĚÄ žúĄžĻėžóź žĄ§žĻėÍįÄ žöįžĄ†ž†ĀžúľŽ°ú ŽźėžĖīžēľ Ūē† Í≤ÉžĚīŽč§. žó¨ÍłįžĄú ž£ľŽ™©Ūē† ž†źžĚÄ Net3 ÍīÄŽßĚžĚė žė§Ž•łž™Ĺ žēĄŽěėŽ∂ÄŽ∂Ą(ÍīÄŽßź)žóź žú†ŪĖ•žĚė ŽĮľÍįźŽŹĄÍįÄ ŽÜížĚÄ ÍīÄžĚī ŽįÄžßĎŽźėžĖī žěąŽč§ŽäĒ ž†źžĚīŽč§. žĚīŽäĒ ŪÉĪŪĀ¨ÍįÄ ž£ľŽ≥Äžóź žĄ§žĻėŽźėžĖīžěąžĖī žĚľžĚľ žąėžöĒŽüČžĚė Ž≥ÄŽŹôžóź ŽĒįŽ•ł Í≤įÍ≥ľŽ°ú ŪĆźŽč®ŽźúŽč§. Ž≥ł žóįÍĶ¨žóźžĄúŽäĒ Fig. 7žÉĀžĚė ŽĮľÍįźŽŹĄ ÍĶ¨Ž∂ĄžĚĄ (0.5, 0.5)Ž°ú žąėŪĖČŪēėžėÄŽč§. ŽĒįŽĚľžĄú P269ÍįôžĚÄ Í≤Ĺžöį Í≥Ąžł°Íłį žĄ§žĻė Ž≤ĒžúĄ Žāīžóź žÜćŪēėžßÄ Ž™ĽŪēėŽäĒ Í≤įÍ≥ľÍįÄ Žāėžė§Í≤Ć ŽźúŽč§. Í∑łŽü¨Žāė P269žó≠žčú ž†ēžÉĀžčú žú†ŪĖ•žĚė ŽĮľÍįźŽŹĄÍįÄ ŽāģŽč§ÍįÄ ŽĻĄžÉĀžčú ÍłČÍ≤©Ūěą ž¶ĚÍįÄŪēėŽäĒ ÍīÄŽ°úžěĄžĚĄ Ž∂Äž†ēŪē† žąėŽäĒ žóÜŽč§. ŽĒįŽĚľžĄú Í≥Ąžł°Íłį žĄ§žĻėžĚė Ž™©ž†Āžóź ŽĒįŽĚľ ž†Āž†ąŪēú ÍįÄž§ĎžĻėŽ•ľ ž†Āžö©Ūēėžó¨ Ž≥ł Žį©Ž≤ēŽ°†žĚĄ ž†Āžö©ŪēúŽč§Ž©ī Ž≥īŽč§ Ūē©Ž¶¨ž†ĀžĚł Í≥Ąžł°Íłį žĄ§žĻė žßÄž†źžĚė žĄ†ŪÉĚžĚī Žź† Í≤ÉžúľŽ°ú ŪĆźŽč®ŽźúŽč§.
Ž≥łžóįÍĶ¨žóźžĄúŽäĒ ÍīÄŽ°ú Žāī žú†ŪĖ•žĚė Ž≥ÄŽŹôžĚī žč¨Ūēú Ž∂ÄŽ∂ĄžĚĄ ŽĮľÍįźŪēėŽč§Í≥† ŪĆźŽč®ŪēėžėÄžúľŽ©į ž†ēžÉĀž†ĀžĚł žÉĀŪô©žóźžĄú žú†ŪĖ•žĚė Ž≥ÄŽŹôžĚī žóÜŽč§ÍįÄ ŽĻĄž†ēžÉĀžÉĀŪô©(ÍīÄŽ°úžĚė ŪĆĆÍīī)žóź ŽĒįŽĚľ ÍīÄŽ°ú Žāī žú†ŪĖ• Ž≥ÄŽŹôžĚī žč¨ŪēīžßÄŽäĒ ÍīÄŽ°úžóź žöįžĄ†ž†ĀžúľŽ°ú žąėžßąÍ≥Ąžł°ÍłįŽ•ľ žĄ§žĻėŪēėŽäĒ Žį©Ž≤ēŽ°†žĚĄ ž†úžēąŪēėžėÄŽč§. ž†úžēąŽźú Žį©Ž≤ēŽ°†žĚė ž†Āžö© ŽįŹ Í≤įÍ≥ľŽ•ľ ŽŹĄž∂úŪēėÍłį žúĄŪēėžó¨ ŽĆÄŪĎúž†ĀžĚł ÍįÄžÉĀÍīÄŽß̞̳ Mays‚Äôs NetworkžôÄ Net3 ÍīÄŽß̞󟞥ú ž†ąž†źžĚė žąėžöĒŽüČ ŽįŹ ŽĻĄž†ēžÉĀžÉĀŪô©žĚĄ ÍįÄž†ēŪēėžó¨ ž†Āžö©ŪēėžėÄŽč§. Net3 ž†Āžö© Í≤įÍ≥ľ ž†ēžÉĀ ŽįŹ ŽĻĄž†ēžÉĀžÉĀŪô© ŽĎź Í≤Ĺžöį Ž™®ŽĎź ŽĮľÍįźŪēú ÍīÄžĚī Žč§žąė ž°īžě¨ŪēėŽ©į ŽĻĄž†ēžÉĀžĚł Í≤ĹžöįžóźŽßĆ ŽĮľÍįźŽŹĄÍįÄ ŪĀį ÍīÄŽ°úŽäĒ žīĚ 7ÍįúŽ°ú žĄ†ŪÉĚŽźėžóąŽč§.
ž†úžēąŽźú žąėžßąÍ≥Ąžł°Íłį žĄ§žĻėžúĄžĻė Í≤įž†ē Žį©Ž≤ēŽ°†žĚĄ ŪÜĶŪēī žąėŽŹóŽ¨ľ Í≥ĶÍłČÍīÄŽ°ú Žāī žąėžßąŽ¨łž†ú žĚłžßÄŽ•ľ žúĄŪēú ÍįÄžĚīŽďúŽĚľžĚł ŽįŹ ŽĆÄžĚĎŽį©žēą žąėŽ¶ĹžĚė ÍłįžīąžěźŽ£ĆŽ°ú Ūôúžö©ŽźėžĖīžßą žąė žěąžĚĄ Í≤ÉžúľŽ°ú ŪĆźŽč®ŽźúŽč§. ŽėźŪēú, ŽĻĄÍĶźž†Ā ÍįĄŽč®Ūēú Žį©Ž≤ē ŽįŹ Í≥ľž†ēžúľŽ°ú žú†ŪĖ•žĚė Ž≥ÄŽŹô ŽĮľÍįźŽŹĄŽ•ľ ŪĆĆžēÖŪē† žąė žěąžúľŽ©į žĖīŽ†ĶžßÄ žēäÍ≤Ć Í≥Ąžł°ÍłįžĚė žúĄžĻėŽ•ľ žÉĀŽĆÄž†ĀžúľŽ°ú žČĹÍ≤Ć ž†ēŪē† žąė žěąŽč§ŽäĒ ž†źžóźžĄú Ūôúžö© ÍįÄŽä•žĄĪžĚī ž∂©Ž∂ĄŪēú Í≤ÉžúľŽ°ú ŪĆźŽč®ŽźúŽč§. Ž≥ł žóįÍĶ¨žóźžĄúŽäĒ Fig. 7Í≥ľ ÍįôžĚī ÍīÄŽ°úžóź ŽĆÄŪēú ÍįÄž§ĎžĻėŽ•ľ 1Ž°ú ž†Āžö©Ūēėžó¨ (0.5, 0.5)Ž•ľ Íłįž§ÄžúľŽ°ú ÍīÄŽ°úžóź ŽĆÄŪēú ŽĮľÍįźŽŹĄžĚė ž†ēžĚėŽ•ľ ÍĶ¨Ž∂ĄŪēėžėÄŽč§. Í∑łŽü¨Žāė ÍīÄŽ°úžĚė žÉĀŪÉú, žúĄžĻė ŽďĪžĚė ž§ĎžöĒŽŹĄŽ•ľ žāįž†ēŪēėžó¨ ÍįÄž§ĎžĻėŽ•ľ ž†ĀŪē©Ūēú ÍīÄŽ°úŽ≥Ą ÍįÄž§ĎžĻėŽ•ľ Ž∂Äžó¨Ūēėžó¨ Íłįž§ÄžĚĄ žĄ§ž†ēŪēúŽč§Ž©ī Ž™©ž†Āžóź Ž∂ÄŪē©ŪēėŽäĒ Í≥Ąžł°Íłį žĄ§žĻė žúĄžĻė žĄ†ž†ē Žį©Ž≤ēžĚī Žź† Í≤ÉžúľŽ°ú žėąžÉĀŽźėžĖīžßĄŽč§.
ŪĖ•ŪõĄ Žį©Ž≤ēŽ°†žĚĄ ž†úžēąŪēú Í≤ÉÍ≥ľ ŽćĒŽ∂ąžĖī žč§ž†úžßÄžó≠žóź ž†Āžö©Í≥ľ ŽŹôžčúžóź žĄ§žĻėžúĄžĻė, ž≤īŽ•ėžčúÍįĄ ŽďĪžóź ŽĆÄŪēú ž∂ĒÍįÄ žóįÍĶ¨ÍįÄ žąėŪĖČŽźėžĖīž†łžēľ Ūē† Í≤ÉžúľŽ°ú ŪĆźŽč®ŽźúŽč§.
Íįźžā¨žĚė ÍłÄ
Ž≥ł žóįÍĶ¨ŽäĒ 2018ŽÖĄ ž†ēŽ∂Ä(Í≥ľŪēôÍłįžą†ž†ēŽ≥īŪÜĶžč†Ž∂Ä)žĚė žě¨žõźžúľŽ°ú ŪēúÍĶ≠žóįÍĶ¨žě¨Žč®žĚė žßÄžõźžĚĄ ŽįõžēĄ žąėŪĖČ Žźú žĚīÍ≥ĶŽ∂ĄžēľÍłįžīąžóįÍĶ¨žā¨žóÖ(žÉĚžē†ž≤ęžóįÍĶ¨žā¨žóÖ)žĚė žĄĪÍ≥ľžĚīŽ©į, žĚīžóź Íįźžā¨ŽďúŽ¶ĹŽčąŽč§(NRF-2018R1C1B5046400).
Table 1
Peak Load Factor Per Water Population
| Population using water (Ten thousand people) | 0~1 | 1~2 | 2~5 | 5~10 |
| Peak load rate | 1.51 | 1.45 | 1.40 | 1.36 |
Table 2
Typical Demand Scenario
Table 3
Direct Adjacent Matrix (Example of Senario 9)
Table 4
Mixed Adjacent Matrix in Normal Situation
Table 5
Mixed Adjacent Matrix in Abnormal Situation
Table 6
Flow Sensitivity Result by Normal/Abnormal Pipe
Table 7
Flow Sensitivity Result by Normal/Abnormal Pipe (Net3)
References
Aral, MM, Guan, J, and Maslia, ML (2010) Optimal design of sensor placement in water distribution networks. J Water Resour Plann Manage, Vol. 136, No. 1, pp. 5-18.

Chung, G, Jang, DE, Yoo, DG, Jun, HD, and Kim, JH (2009) Determination of optimal pressure monitoring locations for water distribution systems using entropy theory. Journal of Korea Water Resources Association, Vol. 42, No. 7, pp. 537-546.


Cozzolino, L, Della Morte, R, Palumbo, A, and Pianese, D (2011) Stochastic approaches for sensors placement against intentional contaminations in water distribution systems. Civil Engineering and Environmental Systems, Vol. 28, No. 1, pp. 75-98.

Gueli, R (2006). Predator-Prey model for discrete sensor placement. Proceedings of 8th Annual Water Distribution System Analysis Symposium. Cincinnati, OH, USA.

Kessler, A, Ostfeld, A, and Sinai, G (1998) Detecting accidental contaminations in municipal water networks. J Water Resour Plann Manage, Vol. 124, No. 4, pp. 192-198.

Koch, MW, and McKenna, SA (2011) Distributed sensor fusion in water quality event detection. J Water Resour Plan Manag, Vol. 137, No. 1, pp. 10-19.

Krause, A, Leskovec, J, Isovitsch, S, Xu, J, Guestrin, C, VanBriesen, J, et al (2006). Optimizing sensor placements in water distribution systems using submodular function maximization. Proceedings of 8th Annual Water Distribution System Analysis Symposium. Cincinnati, OH, USA.

Ministry of Environment (ME) (2008). Manual of water demand prediction work (žÉĀžąėŽŹĄ žąėžöĒŽüČ žėąžł° žóÖŽ¨ī Ū鳎ěĆ).

Ostfeld, A, and Salomons, E (2006). Sensor network design proposal for the battle of the water sensor networks (BWSN). Proceedings of 8th Annual Water Distribution System Analysis Symposium. Cincinnati, OH, USA.

Ozger, SS (2003). A semi-pressure-driven approach to reliability assessment of water distribution network. Ph.D. dissertation. Arizona State University; Tempe, AZ, USA.

Propato, M, and Piller, O (2006). Battle of the water sensor networks. Proceedings of 8th Annual Water Distribution System Analysis Symposium. Cincinnati, OH, USA.

Tryby, ME, Propato, M, and Ranjithan, SR (2010) Monitoring design for source identification in water distribution systems. J Water Resour Plann Manage, Vol. 136, No. 6, pp. 637-646.

Watson, JP, Murray, R, and Hart, WE (2009) Formulation and optimization of robust sensor placement problems for drinking water contamination warning systems. Journal of Infrastructure Systems, Vol. 15, No. 4, pp. 330-339.

Xanthopulos, Z, Melachrinoudis, E, and Solomon, MM (2000) Interactive multiobjective group decision making with interval parameters. Management Science, Vol. 46, No. 12, pp. 1585-1601.

- TOOLS
-
METRICS

-
- 1 Crossref
- 3,049 View
- 62 Download
- Related articles in KOSHAM
-
Optimization of Locations of Elevated Tanks for Stable Water Supply Networks2015 December;15(6)