|
 |
- Search
| J. Korean Soc. Hazard Mitig. > Volume 19(7); 2019 > Article |
|
Abstract
This paper proposes a method for generating rainfall ensemble members by considering regional characteristics. The movement directions of storms (characteristic direction) and spatial distribution of rainfall intensity (rainfall-intensity weight) are considered as the regional characteristics. As a case study, grids for the ensemble simulation are set in Seoul, Korea, where the rain-gauge density is quite high. The characteristic direction and rainfall-intensity weight of each grid are determined based on observations of major storm events that occurred in Seoul during the last 10 years. The rainfall ensemble members are generated by considering the characteristic directions quantified using the beta distribution. A total of 100 rainfall ensemble members are generated by repeating the simulation of the storm movement. The result from the simple average of these ensemble members is considered as the ensemble mean. The rainfall ensemble members and ensemble mean are evaluated based on the rainfall-intensity weights. The rainfall ensemble members generated using various types of rainfall fields are found to be very similar to the spatial distribution of the rainfall-intensity weights. The ensemble mean is also found to exhibit average characteristics of the rainfall ensemble members. The same results are also derived from the simulation of the storm event that occurred in 2018.
ņÜöņ¦Ć
ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö ņ¦ĆņŚŁņĀüņØĖ ĒŖ╣ņä▒ņØä Ļ│ĀļĀżĒĢśņŚ¼ Ļ░ĢņÜ░ ņĢÖņāüļĖö ļ®żļ▓äļź╝ ņāØņä▒ĒĢśļŖö ĻĖ░ļ▓ĢņØä ņĀ£ņĢłĒĢśņśĆļŗż. ņ¦ĆņŚŁĒŖ╣ņä▒ņ£╝ļĪ£ļŖö Ļ░ĢņÜ░ņØś ņØ┤ļÅÖļ░®Ē¢źĻ│╝ Ļ░ĢņÜ░Ļ░ĢļÅäņØś Ļ│ĄĻ░äņĀü ļČäĒżļź╝ Ļ│ĀļĀżĒĢśņśĆļŗż. ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö ņĀüņÜ® ņé¼ļĪĆļĪ£ ņ¦ĆņāüņÜ░ļ¤ēĻ│äņØś ļČäĒżļ░ĆļÅäĻ░Ć ņĪ░ļ░ĆĒĢ£ ņä£ņÜĖĒŖ╣ļ│äņŗ£ņŚÉ ļīĆĒĢ┤ ļ¬©ņØś Ļ▓®ņ×Éļ¦ØņØä ĻĄ¼ņČĢĒĢśĻ│Ā, ņĢÖņāüļĖö ĻĖ░ļ▓ĢņØä ņĀüņÜ®ĒĢśņśĆļŗż. Ļ▓®ņ×Éļ│ä ĒŖ╣ņä▒ļ░®Ē¢źĻ│╝ Ļ░ĢņÜ░Ļ░ĢļÅä Ļ░Ćņżæņ╣śļŖö ņĄ£ĻĘ╝ 10ļģä ļÅÖņĢł ļ░£ņāØĒĢ£ ņŻ╝ņÜö ĒśĖņÜ░ņé¼ņāüņØś Ļ┤ĆņĖĪņ×ÉļŻīļź╝ ĒåĀļīĆļĪ£ Ļ▓░ņĀĢĒĢśņśĆļŗż. ņĢÖņāüļĖö ļ®żļ▓äļŖö ĒŖ╣ņä▒ļ░®Ē¢źņØś ĒåĄĻ│äņ╣śļĪ£ļČĆĒä░ ņ£ĀļÅäļÉ£ ļ▓ĀĒāĆļČäĒżļź╝ ĻĖ░ļ░śņ£╝ļĪ£ ņāØņä▒ĒĢśņśĆļŗż. Ļ░ĢņÜ░ņØś ņØ┤ļÅÖļ¬©ņØśļź╝ 100ĒÜī ņłśĒ¢ēĒĢśļ®┤ ņ┤Ø 100Ļ░£ņØś ņĢÖņāüļĖö ļ®żļ▓äĻ░Ć ņāØņä▒ļÉśĻ│Ā, ņØ┤ ņĢÖņāüļĖö ļ®żļ▓äļōżņØä ļŗ©ņł£ĒÅēĻĘĀĒĢ£ Ļ▓░Ļ│╝Ļ░Ć ņĢÖņāüļĖö ĒÅēĻĘĀņØ┤ ļÉ£ļŗż. ņāØņä▒ļÉ£ ņĢÖņāüļĖö ļ®żļ▓äņÖĆ Ļ░ĢņÜ░ ņĢÖņāüļĖö ĒÅēĻĘĀņŚÉ ļīĆĒĢ£ ĒÅēĻ░ĆļŖö Ļ░ĢņÜ░Ļ░ĢļÅä Ļ░Ćņżæņ╣śļź╝ ĻĖ░ņżĆņ£╝ļĪ£ ņłśĒ¢ēļÉśņŚłļŗż. ņŚ¼ļ¤¼ ĒśĢĒā£ņØś Ļ░ĆņāüņØś Ļ░ĢņÜ░ņןņØä ņ×ģļĀźĒĢśņŚ¼ ņāØņä▒ĒĢ£ ņĢÖņāüļĖö ļ®żļ▓äļŖö Ļ░ĢņÜ░Ļ░ĢļÅä Ļ░Ćņżæņ╣śņØś Ļ│ĄĻ░äņĀü ļČäĒżņÖĆ ņāüļŗ╣Ē׳ ņ£Āņé¼ĒĢ©ņØä ĒÖĢņØĖĒĢśņśĆļŗż. ļśÉĒĢ£, Ļ░ĢņÜ░ ņĢÖņāüļĖö ĒÅēĻĘĀņØĆ Ļ░ĢņÜ░ ņĢÖņāüļĖö ļ®żļ▓äļōżņØś ĒÅēĻĘĀņĀüņØĖ ĒŖ╣ņä▒ņØä Ļ░Ćņ¦ĆļŖö Ļ▓āņ£╝ļĪ£ ļéśĒāĆļé¼ļŗż. ņØ┤ļ¤¼ĒĢ£ Ļ▓░Ļ│╝ļŖö 2018ļģäņŚÉ ļ░£ņāØĒĢ£ ņŗżņĀ£ ĒśĖņÜ░ņé¼ņāüņØä ņ×ģļĀźĒĢ£ Ļ▓ĮņÜ░ņŚÉņä£ļÅä ĒÖĢņØĖĒĢĀ ņłś ņ׳ņŚłļŗż.
ņ¦¦ņØĆ ņŗ£Ļ░ä ļÅÖņĢł Ēü░ Ļ░ĢņÜ░ļź╝ ļÅÖļ░śĒĢśļŖö ņ¦æņżæĒśĖņÜ░ņŚÉ ņØśĒĢ┤ ņ£Āļ░£ļÉśļŖö ļÅīļ░£ĒÖŹņłśļŖö ļÅäņŗ£ ļ░Å ņé░ņ¦Ć ņ£ĀņŚŁņŚÉ ļ¦ēļīĆĒĢ£ ņØĖļ¬ģ, ņ×¼ņé░ Ēö╝ĒĢ┤ļź╝ ņĢ╝ĻĖ░ĒĢ£ļŗż(Kim et al., 2007; Lee et al., 2011). ļÅīļ░£ĒÖŹņłśļŖö ļÅäļŗ¼ņŗ£Ļ░äņØ┤ ļ¦żņÜ░ ņ¦¦ņĢä Ļ░ĢņÜ░ ļ░£ņāØ ņ¦üĒøäļĪ£ļČĆĒä░ 1~2ņŗ£Ļ░ä ņØ┤ļé┤ņŚÉ ņ£Āļ░£ļÉśļŖö ĒŖ╣ņä▒ņØ┤ ņ׳ņ¢┤ ņ¦ĆņāüĻ┤ĆņĖĪ Ļ░ĢņÜ░ņ×ÉļŻī Ēś╣ņØĆ ļĀłņØ┤ļŹö Ļ┤ĆņĖĪĻ░ĢņÜ░ņ×ÉļŻīļź╝ ņØ┤ņÜ®ĒĢśļŖö ļŹ░ Ēü░ ĒĢ£Ļ│äĻ░Ć ņ׳ļŗż(NWS, 1998; Choi and Nam, 2005). ņØ┤ļź╝ ĻĘ╣ļ│ĄĒĢśĻĖ░ ņ£äĒĢ┤ ņłśņ╣śņśłļ│┤ļ¬©ĒśĢ ļ░Å Ļ░ĢņÜ░ņśłņĖĪļ¬©ĒśĢņ£╝ļĪ£ļČĆĒä░ ņāØņä▒ļÉ£ ņśłņĖĪĻ░ĢņÜ░ņ×ÉļŻīļź╝ ļÅīļ░£ĒÖŹņłś ņśłĻ▓Įļ│┤ņŚÉ ņØ┤ņÜ®ĒĢ£ļŗż(KMA, 2006; Georgakakos et al., 2013; Smith et al., 2016). ņśłņĖĪĻ░ĢņÜ░ņ×ÉļŻī ņāØņä▒ņŚÉļŖö ņ×ÉļŻīņØś ĒśĢĒā£Ļ░Ć ņ£Āņé¼ĒĢśĻ│Ā, ĒÖ£ņÜ®ņä▒ņØ┤ Ļ░Ćņן ļåÆņØĆ ļĀłņØ┤ļŹö Ļ┤ĆņĖĪĻ░ĢņÜ░Ļ░Ć ņ×ģļĀźņ×ÉļŻīļĪ£ ņØ┤ņÜ®ļÉ£ļŗż. ņØ┤ Ļ│╝ņĀĢņŚÉņä£ ņśłņĖĪĻ░ĢņÜ░ļŖö ļĀłņØ┤ļŹö Ļ┤ĆņĖĪņØ┤ Ļ░Ćņ¦ĆļŖö ņśżņ░©ļź╝ ĻĘĖļīĆļĪ£ ĒżĒĢ©ĒĢśĻ▓ī ļÉ£ļŗż. ļŹöņÜ▒ņØ┤ ņśłņĖĪ ĒÆłņ¦łņØĆ ņśłņĖĪ ņäĀĒ¢ēņŗ£Ļ░äņØ┤ ĻĖĖņ¢┤ņ¦łņłśļĪØ ĻĖēĻ▓®Ē׳ Ļ░ÉņåīĒĢ£ļŗż(Hwang et al., 2013). ņØ┤ņŚÉ ļö░ļØ╝ ņśłņĖĪĻ░ĢņÜ░ņ×ÉļŻīņØś ĒÆłņ¦ł Ē¢źņāüņØä ņ£äĒĢ┤ ņśłņĖĪ ņĢīĻ│Āļ”¼ņ”śņØä Ļ░£ņäĀĒĢ£ļŗżļōĀņ¦Ć ņĢÖņāüļĖö ĻĖ░ļ▓ĢņØä ņĀüņÜ®ĒĢśļŖö ļō▒ņØś ļģĖļĀźņØ┤ ņ¦ĆņåŹņĀüņ£╝ļĪ£ ņØ┤ļŻ©ņ¢┤ņ¦ĆĻ│Ā ņ׳ļŗż(Tracton and Kalnay, 1993; Buizza, 1997; Radhakrishna et al., 2012).
Ēśäņ×¼Ļ╣īņ¦Ć ņ┤łļŗ©ĻĖ░ ņśłņĖĪĻ░ĢņÜ░ņ×ÉļŻīļź╝ ņāØņä▒ĒĢśļŖö ļŗżņ¢æĒĢ£ Ļ░ĢņÜ░ņśłņĖĪļ¬©ĒśĢļōżņØ┤ Ļ░£ļ░£ļÉśņŚłļŗż. ĻĖ░ņāüņ▓ŁņŚÉņä£ļŖö Korea Local Analysis and Prediction System (KLAPS)Ļ│╝ McGill Algorithm for Precipitation Nowcasting by Lagrangian Extrapolation (MAPLE)Ļ│╝ Ļ░ÖņØĆ Ļ░ĢņÜ░ņśłņĖĪļ¬©ĒśĢņØä ĻĄ¼ņČĢĒĢśņŚ¼ ņ┤łļŗ©ĻĖ░ ņśłļ│┤ņŚÉ ĒÖ£ņÜ®ĒĢśĻ│Ā ņ׳ļŗż. KLAPSļŖö ļ»ĖĻĄŁ National Oceanic and Atmospheric Administration (NOAA)ņØś ĻĄŁņ¦Ć ĻĘ£ļ¬© ĻĖ░ņāüņ×ÉļŻī ņ▓śļ”¼ ļ░Å ļČäņäØņŗ£ņŖżĒģ£ņØĖ Local Analysis and Prediction System (LAPS)ņØä ņżæĻĘ£ļ¬© ņśłņĖĪļ¬©ĒśĢĻ│╝ Ļ▓░ĒĢ®ĒĢśņŚ¼ ĻĄŁļé┤ņØś ņŗżņĀĢņŚÉ ļ¦×Ļ▓ī ņ×¼ĻĄ¼ņä▒ĒĢ£ Ļ░ĢņÜ░ņśłņĖĪ ņŗ£ņŖżĒģ£ņ£╝ļĪ£ņŹ©, 3ņŗ£Ļ░ä Ļ░äĻ▓®ņØś ņśłņĖĪņ×ÉļŻīļź╝ ņĀ£Ļ│ĄĒĢ£ļŗż(KMA, 2008; NIMS, 2009). MAPLEņØĆ ļ│ĆļČäņŚÉņĮöņČöņĀü ĻĖ░ļ▓Ģ(variational echo tracking technique)ņØä ņØ┤ņÜ®ĒĢśņŚ¼ Ļ░Ģņłś ņŚÉņĮöņØś ņØ┤ļÅÖļ▓ĪĒä░ļź╝ ņé░ņČ£ĒĢśĻ│Ā Semi-Lagrangian ļ░®ļ▓ĢņØä ĒåĄĒĢ┤ ņłś ņŗ£Ļ░ä ņØ┤ļé┤ Ļ░Ģņłś ņŚÉņĮöņØś ņ£äņ╣śļź╝ ņśłņĖĪĒĢ£ļŗż(Germann and Zawadzki, 2002). ņØ┤ņÖĖņŚÉļÅä ņśüĻĄŁ ĻĖ░ņāüņ▓Łņ£╝ļĪ£ļČĆĒä░ ļÅäņ×ģĒĢ£ Unified Model (UM), ņØ╝ļ│Ė ĻĖ░ņāüņ▓ŁņØś ĒśäņŚģ ļ¬©ĒśĢņØĖ Very Short-Range Forecast of precipitation (VSRF) ļ¬©ĒśĢ, ļ»ĖĻĄŁ ĻĖ░ņāüņ▓ŁĻ│╝ Ļ│ĄļÅÖ Ļ░£ļ░£ĒĢ£ System for Convection Analysis and Nowcasting (SCAN) ļ¬©ĒśĢ ļō▒ņØä ņÜ┤ņśüĒĢ£ ļ░ö ņ׳ļŗż(NIMR, 2008; Han, 2014; Kim et al., 2015). ĻĄŁņÖĖņŚÉņä£ļÅä Auto Now Caster (ANC)ņÖĆ Thunderstorm Environment Strike Probability Algorithm (THESPA), Thunderstorm Identification, Tracking, Analysis and Nowcasting (TITAN) ļō▒ Ļ░ĢņÜ░ņśłņĖĪļ¬©ĒśĢņØ┤ Ļ░£ļ░£ļÉśņ¢┤ ņÜ┤ņśüļÉśĻ│Ā ņ׳ļŗż(Dixon and Wiener, 1993; Mueller et al., 2003; Dance et al., 2010).
ņśłņĖĪĻ░ĢņÜ░ļŖö ļČłĒÖĢņŗżņä▒, ĒÄĖņØśļź╝ Ļ░Ćņ¦ł ņłśļ░¢ņŚÉ ņŚåĻĖ░ ļĢīļ¼ĖņŚÉ ņĢäņ¦üĻ╣īņ¦ĆļÅä ņĀüņĀĢ ņłśņżĆņØś ņśłņĖĪ ĒÆłņ¦łņØä ĒÖĢļ│┤ĒĢśņ¦Ć ļ¬╗ĒĢśĻ│Ā ņ׳ļŗż(Seo, 2010; Kang et al., 2017). ņśłņĖĪĻ░ĢņÜ░ļŖö ļĀłņØ┤ļŹö Ļ┤ĆņĖĪĻ░ĢņÜ░ļĪ£ļČĆĒä░ ņāØņä▒ļÉśĻĖ░ ļĢīļ¼ĖņŚÉ Ļ┤ĆņĖĪ Ļ│╝ņĀĢņŚÉņä£ ļ░£ņāØĒĢśļŖö Ļ┤ĆņĖĪņśżņ░©, ņ¦ĆņāüĻ┤ĆņĖĪņ╣śņÖĆņØś ĒÄĖņØś ļō▒ ļĀłņØ┤ļŹö Ļ░ĢņÜ░Ļ░Ć Ļ░Ćņ¦ĆļŖö ĒĢ£Ļ│äņŚÉ ņØśĒĢ£ ņśżņ░©ļź╝ ĻĘĖļīĆļĪ£ Ļ░Ćņ¦ĆĻ▓ī ļÉ£ļŗż. ļśÉĒĢ£, ļīĆĻĖ░ļŖö ļ╣äņäĀĒśĢ ļ░Å Ēś╝ļÅł(chaotic) ņŗ£ņŖżĒģ£ņØ┤ļ»ĆļĪ£ Ļ░ĢņÜ░ņןņØś ļ░£ļŗ¼Ļ│╝ ņØ┤ļÅÖļ▓ĪĒä░ļź╝ ļ¬©ņØśĒĢśļŖö Ļ│╝ņĀĢņŚÉņä£ļÅä ļ¦ÄņØĆ ļČłĒÖĢņŗżņä▒ņØä ļé┤ĒżĒĢśĻ▓ī ļÉ£ļŗż(Lorenz, 1969; Seed, 2003). ĒŖ╣Ē׳ ļīĆļźś ļČłņĢłņĀĢņ£╝ļĪ£ ļ░£ņāØĒĢśļŖö ĻĄŁņ¦ĆņĀüņØĖ ņ¦æņżæĒśĖņÜ░ņŚÉ ļīĆĒĢ£ ņśłņĖĪņä▒ļŖźņØĆ ļé«ņØĆ Ļ▓āņ£╝ļĪ£ ņĢīļĀżņĀĖ ņ׳ļŗż(Saito et al., 2011). ļŹöņÜ▒ņØ┤ ņśłņĖĪĻ░ĢņÜ░ņØś ļČłĒÖĢņŗżņä▒ņØĆ ņśłņĖĪ ņäĀĒ¢ēņŗ£Ļ░ä, Ļ░ĢņÜ░ņé¼ņāüņØś Ēü¼ĻĖ░ ļ░Å ņ£ĀņŚŁņØś ĒŖ╣ņä▒ņŚÉ ļö░ļØ╝ ļŗżļź┤Ļ▓ī ļéśĒāĆļéśļ®░ ņØ╝ļ░śņĀüņØĖ Ļ▓ĮĒ¢ź ļśÉĒĢ£ ļ¬ģĒÖĢĒĢśņ¦Ć ņĢŖļŗż(Collier, 2009).
ņśłņĖĪĻ░ĢņÜ░ņØś ĒÆłņ¦łņØä Ļ░£ņäĀĒĢśĻĖ░ ņ£äĒĢ£ ĒĢśļéśņØś ļ░®ņĢłņ£╝ļĪ£ņŹ© ņĢÖņāüļĖö ņśłņĖĪĻĖ░ļ▓ĢņØ┤ ĒÖ£ņÜ®ļÉ£ļŗż. ņĢÖņāüļĖö ņśłņĖĪņØ┤ļ×Ć, ĒĢ£ ņŗ£ņĀÉņŚÉ ļīĆĒĢ┤ ņśłņĖĪļÉ£ ļæÉ Ļ░£ ņØ┤ņāüņØś ņ×ÉļŻīļōżņØä Ļ▓░ĒĢ®ĒĢśņŚ¼ ļŹö ļø░ņ¢┤ļé£ ņśłņĖĪ ĒÆłņ¦łņØä Ļ░Ćņ¦ĆļŖö ņśłņĖĪņ╣śļź╝ ņČöņĀĢĒĢ┤ļé┤ļŖö ĻĖ░ļ▓ĢņØ┤ļŗż(Sivillo et al., 1997; KMA, 2012). ņĢÖņāüļĖö ņśłņĖĪĻĖ░ļ▓ĢņØĆ Ļ▓░ņĀĢļĪĀņĀüņØĖ Ļ░ÆņØä ņĀ£ņŗ£ĒĢśļŖö ņłśņ╣śĻĖ░ņāüņśłņĖĪņØś ļČłĒÖĢņŗżņä▒ņØä ņ¢┤ļŖÉ ņĀĢļÅä ņżäņØ╝ ņłś ņ׳ļŗż(Migliorini et al., 2011; Baker et al., 2014). ļśÉĒĢ£, ļ░£ņāØ ĒÖĢļźĀņØĆ ļé«ņ¦Ćļ¦ī ĻĘ£ļ¬©Ļ░Ć Ēü░ ĻĘ╣ņ╣ś Ļ░ĢņÜ░ņŚÉ ļīĆĒĢ£ Ļ░ĢņÜ░ ļ░£ņāØ ņŗ£ļéśļ”¼ņśżļź╝ Ļ│ĀļĀżĒĢĀ ņłś ņ׳ļŗżļŖö ņןņĀÉņØ┤ ņ׳ļŗż. ļŹö ļéśņĢäĻ░Ć ĻĖ┤ ņäĀĒ¢ēņŗ£Ļ░äņŚÉ ļīĆĒĢ£ ņśłņĖĪņä▒ņØś Ē¢źņāüļ┐Éļ¦ī ņĢäļŗłļØ╝ ņśłņĖĪņØś ļČłĒÖĢņŗżņä▒ņŚÉ ļīĆĒĢ£ ņĀĢļ│┤ļÅä ĒĢ©Ļ╗ś ņĀ£Ļ│ĄĒĢĀ ņłś ņ׳ļŗż(Molteni et al., 1996; Hewitt, 2004). Ļ▓░ĻĄŁ, ņĢÖņāüļĖö ņśłņĖĪņØĆ ņłśņ╣śĻĖ░ņāüņśłņĖĪņØ┤ ņĀ£Ļ│ĄĒĢśļŖö Ļ▓░ņĀĢļĪĀņĀüņØĖ ņśłņĖĪņ╣śņŚÉļ¦ī ņØśņĪ┤ĒĢśļŖö Ļ▓āņØ┤ ņĢäļŗłļØ╝ ņŚ¼ļ¤¼ ņśłņĖĪņ╣śļź╝ ĒÖĢļźĀļĪĀņĀüņ£╝ļĪ£ Ļ▓░ĒĢ®ĒĢśņŚ¼ ļŹöņÜ▒ ņŗĀļó░ņä▒ ņ׳ļŖö Ļ▓░Ļ│╝ļź╝ ļÅäņČ£ĒĢśļŖö ļŹ░ņŚÉ ĻĘĖ ļ¬®ņĀüņØ┤ ņ׳ļŗżĻ│Ā ĒĢĀ ņłś ņ׳ļŗż. ņØ┤ņÖĆ Ļ░ÖņØĆ ņןņĀÉņØä Ļ░Ćņ¦ĆĻĖ░ņŚÉ Ēśäņ×¼ ĻĄŁņÖĖņØś ņŚ¼ļ¤¼ ĒśäņŚģ ĻĖ░Ļ┤ĆļōżņŚÉņä£ļŖö ņĢÖņāüļĖö ņśłņĖĪĻĖ░ļ▓ĢņØä ĻĖ░ņāüņśłļ│┤ņŚÉ ņĀüĻĘ╣ņĀüņ£╝ļĪ£ ĒÖ£ņÜ®ĒĢśĻ│Ā ņ׳ļŗż(Richardson, 2000; Bowler et al., 2008; Kay et al., 2013).
Ļ│ĄĻĄÉļĪŁĻ▓īļÅä ĻĖ░ņĪ┤ņØś Ļ░ĢņÜ░ ņĢÖņāüļĖö ņśłņĖĪĻĖ░ļ▓Ģ ņżæ ņ¦ĆņŚŁĒŖ╣ņä▒ņØä Ļ│ĀļĀżĒĢ£ ņé¼ļĪĆļŖö ņ░ŠņĢäļ│┤ĻĖ░ ņ¢┤ļĀĄļŗż. ļīĆļČĆļČäņØś ņŚ░ĻĄ¼ļŖö ņ░ĖĻ░Æņ£╝ļĪ£ Ļ░ĆņĀĢļÉśļŖö Ļ┤ĆņĖĪņ╣śņŚÉ ĒÖĢļźĀļĪĀņĀü ņäŁļÅÖņØä ņČöĻ░ĆĒĢśĻ▒░ļéś ņŚ¼ļ¤¼ ļ¬©ĒśĢņ£╝ļĪ£ļČĆĒä░ ņāØņä▒ļÉ£ ņśłņĖĪĻ░ĢņÜ░ņŚÉ ņĢÖņāüļĖö ĻĖ░ļ▓ĢņØä ņĀüņÜ®ĒĢśļŖö ļō▒ ņŻ╝ļĪ£ ņśłņĖĪņ×ÉļŻīņØś ņØ┤ņÜ®ņŚÉļ¦ī ņ¦æņżæĒĢśņśĆļŗż(Leith, 1974; Tribbia and Baumhefner, 1988; Duan et al., 2007; Kang et al., 2017). Ļ░ĢņÜ░ņśłņĖĪļ¬©ĒśĢņØś ņśłņĖĪĻ░ĢņÜ░ ņāØņä▒ņŚÉ ņ׳ņ¢┤ņä£ļÅä ĒśĖņÜ░ņé¼ņāüņØś ĻĖ░ņāüĒĢÖņĀü ĒŖ╣ņä▒ļ¦īņØä Ļ│ĀļĀżĒĢśļŖö Ļ▓ĮņÜ░Ļ░Ć ļ¦ÄņĢśļŗż(Dixon and Wiener, 1993; Germann and Zawadzki, 2002; K-Water, 2005; NIMS, 2009). ĻĘĖļ¤¼ļéś ņ¢┤ļ¢ż ņ¦ĆņŚŁņØś ņ¦ĆĒśĢņĀü, ĻĖ░ĒøäņĀü ĒŖ╣ņä▒ņØĆ ĒśĖņÜ░ņØś ņØ┤ļÅÖ ļ░®Ē¢ź, ņåŹļÅä, Ļ│ĄĻ░äņĀü ļČäĒż ļō▒Ļ│╝ Ļ░ÖņØĆ Ļ░ĢņÜ░ņØś ļ│ĆļÅÖņŚÉ Ēü░ ņśüĒ¢źņØä ļ»Ėņ╣£ļŗż. ĻĘĖļ”¼Ļ│Ā ņØ┤ļ¤¼ĒĢ£ ņ¦ĆņŚŁņĀü ĒŖ╣ņä▒ņØĆ ĒśĖņÜ░ņé¼ņāüņØś ņØ┤ļÅÖ ĒŖ╣ņä▒ņŚÉ ņØ╝ņóģņØś Ļ▓ĮĒ¢źņä▒ņØä ļČĆņŚ¼ĒĢ£ļŗż. ļö░ļØ╝ņä£ ļīĆņāü ņ¦ĆņŚŁņŚÉņä£ ļ░£ņāØĒĢ£ ĒśĖņÜ░ņé¼ņāüņØĆ ņ£Āņé¼ĒĢ£ ņØ┤ļÅÖ ĒŖ╣ņä▒ ļ░Å Ļ│ĄĻ░äņĀü ļČäĒżļź╝ ļ│┤ņØ┤Ļ▓ī ļÉ£ļŗż. ĒĢ┤ļŗ╣ ņ¦ĆņŚŁņŚÉņä£ ļ░£ņāØĒĢĀ ļ»ĖļלņØś ĒśĖņÜ░ņé¼ņāü ļśÉĒĢ£ Ļ│╝Ļ▒░ņŚÉ ļ░£ņāØĒĢ£ ĒśĖņÜ░ņé¼ņāüņØś ĒŖ╣ņä▒ņØä ļö░ļź╝ Ļ░ĆļŖźņä▒ņØ┤ ļ¦żņÜ░ ļåÆļŗż. ļö░ļØ╝ņä£ ņ¦ĆņŚŁĒŖ╣ņä▒ņØä Ļ│ĀļĀżĒĢ£ Ļ░ĢņÜ░ ņĢÖņāüļĖö ņśłņĖĪņØĆ Ļ░ĢņÜ░ ņśłņĖĪ ĒÆłņ¦łņØä Ē¢źņāüņŗ£Ēé¼ ņłś ņ׳ļŖö ĒĢśļéśņØś ļ░®ņĢłņ£╝ļĪ£ ņØ┤ņÜ®ļÉĀ ņłś ņ׳ļŗż.
ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö ņ¦ĆņŚŁņĀüņØĖ ĒŖ╣ņä▒ņØä Ļ│ĀļĀżĒĢśņŚ¼ Ļ░ĢņÜ░ ņĢÖņāüļĖö ļ®żļ▓äļź╝ ņāØņä▒ĒĢśļŖö ĻĖ░ļ▓ĢņØä ņĀ£ņĢłĒĢśĻ│Ā ņāØņä▒ļÉ£ Ļ░ĢņÜ░ ņĢÖņāüļĖö ļ®żļ▓äņŚÉ ļīĆĒĢ£ ĒÅēĻ░Ćļź╝ ņłśĒ¢ēĒĢśĻ│Āņ×É ĒĢ£ļŗż. ņ¦ĆņŚŁĒŖ╣ņä▒ņ£╝ļĪ£ļŖö Ļ▓®ņ×Éļ│ä Ļ░ĢņÜ░ņØś ņØ┤ļÅÖļ░®Ē¢źĻ│╝ Ļ░ĢņÜ░Ļ░ĢļÅäļź╝ Ļ│ĀļĀżĒĢ£ļŗż. ļīĆņāü ņ¦ĆņŚŁņŚÉ ļīĆĒĢ┤ ļ¬©ņØś Ļ▓®ņ×Éļ¦ØņØä ĻĄ¼ņČĢĒĢśĻ│Ā Ļ▓®ņ×Éļ│äļĪ£ ĒŖ╣ņä▒ļ░®Ē¢ź, Ļ░ĢņÜ░Ļ░ĢļÅä Ļ░Ćņżæņ╣śļź╝ Ļ▓░ņĀĢĒĢ£ļŗż. Ļ▓░ņĀĢļÉ£ Ļ▓®ņ×Éļ│ä Ļ░Ćņżæņ╣śņØś ĒåĄĻ│äĒĢÖņĀü ĒŖ╣ņä▒ņ╣śļź╝ ņØ┤ņÜ®ĒĢśņŚ¼ ļ▓ĀĒāĆļČäĒżļź╝ ņ£ĀļÅäĒĢśĻ│Ā, ņØ┤ļĪ£ļČĆĒä░ ņāØņä▒ļÉ£ ļé£ņłśļź╝ ĻĖ░ļ░śņ£╝ļĪ£ ņ×ģļĀźĻ░ĢņÜ░ņןņØś ņØ┤ļÅÖ ļ¬©ņØśļź╝ ņłśĒ¢ēĒĢ£ļŗż. Ļ░ĢņÜ░ ņØ┤ļÅÖ ļ¬©ņØśļŖö ņ×ģļĀźĻ░ĢņÜ░ņןņØä ņØ╝ņĀĢĒĢ£ ļ░®Ē¢źņ£╝ļĪ£ ņØ┤ļÅÖņŗ£Ēéżļ®░ ņØ┤ņĀä ņŚ┤ņØś Ļ░ĢņÜ░Ļ░ĢļÅäļź╝ ļŗżņØī ņŚ┤ļĪ£ ļČäĒĢĀĒĢśņŚ¼ ņĀäņØ┤ĒĢśļŖö ņØ╝ļĀ©ņØś Ļ│╝ņĀĢņØä ņØśļ»ĖĒĢ£ļŗż. ņ×ģļĀźĻ░ĢņÜ░ņןņØś ņØ┤ļÅÖ ļ¬©ņØśĻ░Ć ļüØļé£ Ļ▓░Ļ│╝ļĪ£ ļéśĒāĆļéśļŖö Ļ░ĢņÜ░ņןņØĆ Ļ░ĢņÜ░ ņĢÖņāüļĖö ļ®żļ▓äņŚÉ ĒĢ┤ļŗ╣ĒĢ£ļŗż. ņĄ£ņóģņĀüņ£╝ļĪ£ ņāØņä▒ļÉ£ Ļ░ĢņÜ░ ņĢÖņāüļĖö ļ®żļ▓äņÖĆ Ļ░ĢņÜ░ ņĢÖņāüļĖö ĒÅēĻĘĀņØĆ Ļ░ĢņÜ░Ļ░ĢļÅä Ļ░Ćņżæņ╣śļź╝ ĻĖ░ņżĆņ£╝ļĪ£ ļ╣äĻĄÉ ļ░Å ĒÅēĻ░ĆļÉ£ļŗż. ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö ņÜ░ļ”¼ļéśļØ╝ņŚÉņä£ ņ¦ĆņāüĻ┤ĆņĖĪņåīņØś ļ░ĆļÅäĻ░Ć Ļ░Ćņן ļåÆņ£╝ļ®░, Ļ│ĄĻ░äņĀüņ£╝ļĪ£ Ļ│Āļź┤Ļ▓ī ļČäĒżļÉśņ¢┤ņ׳ļŖö ņä£ņÜĖĒŖ╣ļ│äņŗ£ļź╝ ļīĆņāü ņ¦ĆņŚŁņ£╝ļĪ£ ņäżņĀĢĒĢśņŚ¼ Ļ░ĢņÜ░ ņĢÖņāüļĖö ļ®żļ▓äļź╝ ņāØņä▒ĒĢśĻ│Ā ĒÅēĻ░ĆĒĢśņśĆļŗż.
ņ¦ĆņŚŁĒŖ╣ņä▒ Ļ░Ćņżæņ╣śļź╝ Ļ▓░ņĀĢĒĢśļŖö Ļ▓ĮņÜ░, ļ¬©ņØś Ļ▓®ņ×Éļ¦ØņØä ĻĄ¼ņČĢĒĢśņŚ¼ ņØ┤ņÜ®ĒĢśļŖö Ļ▓āņØ┤ ĒÜ©Ļ│╝ņĀüņØ┤ļŗż. ņ”ē, ļīĆņāü ņ¦ĆņŚŁņØä Ļ▓®ņ×ÉļĪ£ ņäĖļČäĒÖöĒĢ£ Ēøä Ļ▓®ņ×Éļ¦łļŗż Ļ░Ćņżæņ╣śļź╝ Ļ▓░ņĀĢĒĢśļŖö Ļ▓āņØ┤ļŗż. ņØ┤ Ļ▓®ņ×ÉļŖö ĒøäņŚÉ ņ¦ĆņŚŁĒŖ╣ņä▒ņØä Ļ│ĀļĀżĒĢ£ Ļ░ĢņÜ░ņןņØś ņØ┤ļÅÖ ļ¬©ņØśņŚÉļÅä ļÅÖņØ╝ĒĢśĻ▓ī ņĀüņÜ®ļÉ£ļŗż. ļö░ļØ╝ņä£ Ļ▓®ņ×ÉņØś Ēü¼ĻĖ░ļŖö Ļ░ĢņÜ░ņןņØś ņØ┤ļÅÖ ļ¬©ņØśņŚÉ ņĀüņĀłĒĢ£ ņłśņżĆņ£╝ļĪ£ Ļ▓░ņĀĢļÉśņ¢┤ņĢ╝ ĒĢ£ļŗż. Ļ▓®ņ×ÉņØś Ēü¼ĻĖ░Ļ░Ć Ļ│╝ļÅäĒĢśĻ▓ī Ēü¼ļ®┤ ĒśĖņÜ░ņé¼ņāüņØś Ļ│ĄĻ░äņĀü ļČäĒżļź╝ ņČ®ļČäĒ׳ Ļ│ĀļĀżĒĢĀ ņłś ņŚåĻ▓ī ļÉśĻ│Ā, ļ░śļīĆļĪ£ Ļ▓®ņ×ÉņØś Ēü¼ĻĖ░ļéś ļäłļ¼┤ ņ×æņ£╝ļ®┤ Ļ│äņé░ ĒÜ©ņ£©ņØ┤ ļ¢©ņ¢┤ņ¦ł ņłś ņ׳ļŗż. ĻČüĻĘ╣ņĀüņ£╝ļĪ£, Ļ▓®ņ×ÉņØś Ēü¼ĻĖ░ļŖö ņŚ░ĻĄ¼ņØś ļ¬®ņĀüĻ│╝ ņ×ģļĀźļÉśļŖö ņ×ÉļŻīņØś ĒŖ╣ņä▒ ļō▒ņØä Ļ│ĀļĀżĒĢśņŚ¼ Ļ▓░ņĀĢļÉśņ¢┤ņĢ╝ ĒĢ£ļŗż.
ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ņØś ņ¦ĆņŚŁĒŖ╣ņä▒ Ļ░Ćņżæņ╣śļ×Ć, Ļ▓®ņ×Éļ│äļĪ£ Ļ▓░ņĀĢļÉ£ ĒśĖņÜ░ņØś ĒŖ╣ņä▒ļ░®Ē¢źĻ│╝ Ļ░ĢņÜ░Ļ░ĢļÅä Ļ░Ćņżæņ╣śļź╝ ļ¦ÉĒĢ£ļŗż. ĒŖ╣ņä▒ļ░®Ē¢źņØ┤ļ×Ć ļīĆņāü ņ¦ĆņŚŁņØä ĒåĄĻ│╝ĒĢ£ ĒśĖņÜ░ņé¼ņāüņØś ļ░®Ē¢źņä▒ņØä ļīĆĒæ£ĒĢśļŖö Ļ░ÆņØ┤ļŗż. ņ”ē, Ļ│╝Ļ▒░ņŚÉ ļ░£ņāØĒĢ£ ĒśĖņÜ░ņé¼ņāüļōżņØ┤ ņŻ╝ļĪ£ ņØ┤ļÅÖĒĢ£ ļ░®Ē¢źņŚÉ ĒĢ┤ļŗ╣ĒĢ£ļŗż. ļö░ļØ╝ņä£ ĒŖ╣ņä▒ļ░®Ē¢źņØĆ Ļ│╝Ļ▒░ ĒśĖņÜ░ņé¼ņāüņØś ņØ┤ļÅÖĒŖ╣ņä▒ņØä ļČäņäØĒĢśņŚ¼ Ļ▓®ņ×Éļ│äļĪ£ Ļ▓░ņĀĢļÉ£ļŗż. Ļ░ĢņÜ░Ļ░ĢļÅä Ļ░Ćņżæņ╣ś ļśÉĒĢ£ ĒŖ╣ņä▒ļ░®Ē¢źĻ│╝ ņ£Āņé¼ĒĢ£ ļ░®ļ▓Ģņ£╝ļĪ£ Ļ▓░ņĀĢļÉ£ļŗż. Ļ│╝Ļ▒░ņŚÉ ļ░£ņāØĒĢ£ ĒśĖņÜ░ņé¼ņāüņØś Ļ│ĄĻ░äņĀü Ļ░ĢņÜ░ļČäĒżļź╝ ļČäņäØĒĢśņŚ¼ Ļ▓®ņ×Éļ│äļĪ£ Ļ░Ćņżæņ╣śĻ░Ć Ļ▓░ņĀĢļÉ£ļŗż. ņ”ē, ņ¢┤ļ¢ż Ļ▓®ņ×ÉņŚÉ Ļ░ĢņÜ░Ļ░ĢļÅä Ļ░Ćņżæņ╣śĻ░Ć Ēü¼ļ®┤ ĒĢ┤ļŗ╣ Ļ▓®ņ×ÉņŚÉ Ļ░ĢņÜ░Ļ░Ć ņ¦æņżæļÉśļŖö Ļ▓ĮĒ¢źņØ┤ Ēü¼ļŗżļŖö Ļ▓āņØä ņØśļ»ĖĒĢ£ļŗż. ņČöĻ░ĆļĪ£, ņ¦ĆņŚŁĒŖ╣ņä▒ Ļ░Ćņżæņ╣śņØĖ ĒŖ╣ņä▒ļ░®Ē¢źĻ│╝ Ļ░ĢņÜ░Ļ░ĢļÅä Ļ░Ćņżæņ╣śĻ░Ć ņä£ļĪ£ Ēü░ ņāüĻ┤ĆņØ┤ ņ׳ļŗżļŖö ņĀÉļÅä ĻĖ░ņ¢ĄĒĢĀ ĒĢäņÜöĻ░Ć ņ׳ļŗż. ĒŖ╣ņä▒ļ░®Ē¢źņØ┤ ņĀüņĀłĒ׳ ņČöņĀĢļÉśņŚłļŗżļ®┤ Ļ│ĄĻ░äņĀüņ£╝ļĪ£ ĻĘĀņ¦łĒĢ£ ļŗ©ņ£ä Ļ░ĢņÜ░ļź╝ ņ×ģļĀźņ£╝ļĪ£ ĒĢ£ ļ¬©ņØśĻ▓░Ļ│╝ļŖö Ļ░ĢņÜ░Ļ░ĢļÅä Ļ░Ćņżæņ╣śņÖĆ Ēü░ ņāüĻ┤Ćņä▒ņØä Ļ░ĆņĀĖņĢ╝ ĒĢ£ļŗż. ņØ┤ļ¤¼ĒĢ£ ņāüĻ┤Ćņä▒ņØĆ ļ│Ė ņŚ░ĻĄ¼ņØś Ļ▓░Ļ│╝ļź╝ Ļ▓Ćņ”ØĒĢśļŖö Ļ│╝ņĀĢņŚÉņä£ ņŗ¼ļÅä ņ׳Ļ▓ī Ļ▓ĆĒåĀļÉĀ Ļ▓āņØ┤ļŗż.
ņĢ×ņä£ ņ¢ĖĻĖēĒĢ£ Ļ▓āņ▓śļ¤╝, ĒŖ╣ņä▒ļ░®Ē¢źņØĆ ļīĆņāü ņ¦ĆņŚŁņØś Ļ│╝Ļ▒░ ņŻ╝ņÜö ĒśĖņÜ░ņé¼ņāüņŚÉ ļīĆĒĢ£ ļĀłņØ┤ļŹö Ļ░ĢņÜ░ņ×ÉļŻīļéś ņ¦ĆņāüĻ┤ĆņĖĪ Ļ░ĢņÜ░ņ×ÉļŻīļź╝ ļČäņäØĒĢśņŚ¼ Ļ▓░ņĀĢĒĢĀ ņłś ņ׳ļŗż. ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö Ļ│╝Ļ▒░ ņŻ╝ņÜö ĒśĖņÜ░ņé¼ņāüņØś 10ļČä Ļ░äĻ▓® ņ¦ĆņāüĻ┤ĆņĖĪ Ļ░ĢņÜ░ņ×ÉļŻīļź╝ ņØ┤ņÜ®ĒĢśņśĆļŗż. ņ”ē, ĒśĖņÜ░ņé¼ņāüņØ┤ ļīĆņāü ņ¦ĆņŚŁņŚÉ ņ¦äņ×ģĒĢśņśĆļŗżĻ░Ć ļ╣ĀņĀĖļéśĻ░ł ļĢīĻ╣īņ¦Ć ļ¦ż 10ļČä Ļ░äĻ▓®ņ£╝ļĪ£ ĒśĖņÜ░ņØś ĒśĢĒā£ņÖĆ ņżæņŗ¼ ņ£äņ╣śļź╝ ĒīīņĢģĒĢ£ ļÆż, ņØ┤ļź╝ ĒåĀļīĆļĪ£ ļ¦ż ņŗ£ņĀÉ ĒśĖņÜ░ņØś ņØ┤ļÅÖ ļ░®Ē¢ź ļ░Å ņåŹļÅäļź╝ Ļ▓░ņĀĢĒĢ£ļŗż. Ļ│╝Ļ▒░ ņŻ╝ņÜö ĒśĖņÜ░ņé¼ņāüņŚÉ ļīĆĒĢ┤ ņØ┤ļ¤¼ĒĢ£ ļČäņäØņØä ļ░śļ│ĄĒĢ£ Ēøä ĻĘĖ Ļ▓░Ļ│╝ņŚÉ ņŚŁĻ▒░ļ”¼Ļ░Ćņżæļ▓ĢņØä ņĀüņÜ®ĒĢśņŚ¼ Ļ░ü Ļ▓®ņ×ÉņŚÉņä£ņØś ĒÅēĻĘĀņĀüņØĖ ĒŖ╣ņä▒ļ░®Ē¢źņØä Ļ▓░ņĀĢĒĢśņśĆļŗż. Ļ░ĢņÜ░ ņØ┤ļÅÖ ļ¬©ņØśņŗ£ņŚÉļŖö ĒŖ╣ņä▒ļ░®Ē¢źņØä 0Ļ│╝ 1 ņé¼ņØ┤ņØś ņłśņ╣śļĪ£ ņĀĢļ¤ēĒÖöĒĢ£ļŗż. ņŚ¼ĻĖ░ņä£ 0ņØĆ ļČüņ¬ĮņØä 1ņØĆ ļé©ņ¬ĮņØä ņØśļ»ĖĒĢ£ļŗż.
Ļ░ĢņÜ░Ļ░ĢļÅä Ļ░Ćņżæņ╣śņØś Ļ▓░ņĀĢņŚÉļÅä ļ¦ż 10ļČäļ¦łļŗż Ļ┤ĆņĖĪļÉ£ ņ¦ĆņāüĻ┤ĆņĖĪ Ļ░ĢņÜ░ļ¤ēņØä ņØ┤ņÜ®ĒĢśņśĆļŗż. ņŚŁņŗ£ ņŚŁĻ▒░ļ”¼Ļ░Ćņżæļ▓ĢņØä ņØ┤ņÜ®ĒĢśņŚ¼ Ļ░ü Ļ▓®ņ×Éļ│äļĪ£ 10ļČä Ļ░ĢņÜ░ļ¤ēņØä ņé░ņĀĢĒĢĀ ņłś ņ׳ļŗż. ĒśĖņÜ░ņé¼ņāüļ│äļĪ£ ļ¬©ļōĀ Ļ▓®ņ×ÉņØś ĒÅēĻĘĀ Ļ░ĢņÜ░ļ¤ēņØä ĻĄ¼ĒĢ£ Ēøä ļŗżņØī ņŗØņØä ņĀüņÜ®ĒĢśņŚ¼ Ļ▓®ņ×Éļ│ä Ļ░ĢņÜ░Ļ░ĢļÅä Ļ░Ćņżæņ╣śļź╝ Ļ▓░ņĀĢĒĢĀ ņłś ņ׳ļŗż.
ņŚ¼ĻĖ░ņä£ WRņØĆ Ļ▓®ņ×ÉņØś Ļ░ĢņÜ░Ļ░ĢļÅä Ļ░Ćņżæņ╣śļź╝ ņØśļ»ĖĒĢ£ļŗż. RņØĆ Ļ▓®ņ×ÉņØś ĒÅēĻĘĀ Ļ░ĢņÜ░ļ¤ēņØ┤ļŗż. RmaxņÖĆ RminņØĆ Ļ░üĻ░ü ļ¬©ļōĀ Ļ▓®ņ×ÉņØś ĒÅēĻĘĀ Ļ░ĢņÜ░ļ¤ē ņżæ ņĄ£ļīōĻ░ÆĻ│╝ ņĄ£ņå¤Ļ░ÆņØ┤ļŗż. ņØ┤ Ļ│╝ņĀĢņØä Ļ│ĀļĀżĒĢ£ ļ¬©ļōĀ ĒśĖņÜ░ņé¼ņāüņŚÉ ļīĆĒĢ┤ ļ░śļ│ĄĒĢ£ Ēøä ĒÅēĻĘĀĒĢśļ®┤ Ļ░ü Ļ▓®ņ×Éļ│ä Ļ░ĢņÜ░Ļ░ĢļÅä Ļ░Ćņżæņ╣śĻ░Ć Ļ▓░ņĀĢļÉ£ļŗż. Ļ░ĢņÜ░Ļ░ĢļÅä Ļ░Ćņżæņ╣śļÅä ĒŖ╣ņä▒ļ░®Ē¢źĻ│╝ ļ¦łņ░¼Ļ░Ćņ¦ĆļĪ£ 0Ļ│╝ 1 ņé¼ņØ┤ņØś ņłśņ╣śļĪ£ ņĀĢļ¤ēĒÖöļÉ£ļŗż.
ļ▓ĀĒāĆļČäĒżļŖö ļīĆņāü ņ×ÉļŻīĻ░Ć ņāüĒĢ£Ļ│ä ļ░Å ĒĢśĒĢ£Ļ│äļź╝ Ļ░Ćņ¦ĆļŖö ĒŖ╣ņłśĒĢ£ Ļ▓ĮņÜ░ņŚÉ ņĀüĒĢ®ĒĢ£ ĒÖĢļźĀļČäĒżņØ┤ļŗż(Pearson, 1934). ĻĖ░ņĪ┤ ņŚ░ĻĄ¼ļōżņŚÉņä£ļÅä ņāüŌŗģĒĢśĒĢ£Ļ│äĻ░Ć ļ¬ģĒÖĢĒĢ£ ņ×ÉņŚ░ĒśäņāüņØä ņäżļ¬ģĒĢśļŖö ļŹ░ ļ▓ĀĒāĆļČäĒżĻ░Ć ĒÜ©Ļ│╝ņĀüņ£╝ļĪ£ ņĀüņÜ®ļÉ£ ļ░ö ņ׳ļŗż(Hafley and Schreuder, 1977; Maltamo et al., 1995). ņłśļ¼ĖĒĢÖ ļČäņĢ╝ņŚÉņä£ļÅä ļ▓ĀĒāĆļČäĒżņØś ĒÖ£ņÜ®ņä▒ņØĆ Ēü¼ļŗż. ĒśĖņÜ░ņé¼ņāüņØś ņŗ£Ļ░äļČäĒż ņ£ĀļÅäņŚÉ ņØ┤ņÜ®ļÉśĻ▒░ļéś(Jun and Yoo, 2012, 2013), ĒåĀņ¢æņØ┤ļéś ļīĆņłśņĖĄņØś ĒŖ╣ņä▒ ļ░Å Ļ░Ģņäż ļ®┤ņĀüņØä ņĀĢļ¤ēĒÖöĒĢśĻ│Ā(Beran and Sutcliffe, 1972; Cooke et al., 1995; Brubaker and Menoes, 2001; Ricciardi et al., 2005), ļŗ©ņ£äņ£Āļ¤ēļÅä ļ¬©ĒśĢņØś ĒĢ┤ņäØņŚÉ ņØ┤ņÜ®ļÉ£ ļ░ö ņ׳ļŗż(Bhunya et al., 2004; Bhunya et al., 2007).
ļ▓ĀĒāĆļČäĒżņØś ĒÖĢļźĀļ░ĆļÅäĒĢ©ņłśļŖö ņĢäļלņÖĆ Ļ░Öļŗż.
ņŚ¼ĻĖ░ņä£ ╬▒ņÖĆ ╬▓ļŖö ļ▓ĀĒāĆļČäĒżņØś ĒśĢņāüņØä Ļ▓░ņĀĢĒĢśļŖö ļ¦żĻ░£ļ│ĆņłśņØ┤Ļ│Ā B(╬▒, ╬▓)ļŖö ļ▓ĀĒāĆ ĒĢ©ņłśņØ┤ļŗż. ╬▒, ╬▓ > 0 ņØ╝ ļĢī, ļ▓ĀĒāĆ ĒĢ©ņłś B(╬▒, ╬▓)ļŖö Eq. (3)ņ£╝ļĪ£ ņĀĢļ”¼ļÉ£ļŗż.
ļ¦īņØ╝ ╬▒ = ╬▓ = 1ņØ┤ļ®┤, ņ£ä ļ▓ĀĒāĆļČäĒżļŖö ĻĘĀļō▒ļČäĒż(uniform distribution)ņÖĆ ļÅÖņØ╝ĒĢśļŗż. ļ▓ĀĒāĆļČäĒżļź╝ ļö░ļź┤ļŖö ĒÖĢļźĀļ│Ćņłś xņØś ĒÅēĻĘĀĻ│╝ ļČäņé░ņØĆ ņĢäļלņÖĆ Ļ░ÖņØ┤ ļ¦żĻ░£ļ│Ćņłś ╬▒ņÖĆ ╬▓ļĪ£ ļéśĒāĆļé╝ ņłś ņ׳ļŗż.
ļśÉĒĢ£, ļ▓ĀĒāĆļČäĒżņØś ĒÅēĻĘĀĻ│╝ ļČäņé░ ņé░ņĀĢņŗØņØä ņĪ░ĒĢ®ĒĢśļ®┤ ļŗżņØīĻ│╝ Ļ░ÖņØ┤ ļ¦żĻ░£ļ│Ćņłś ╬▒ņÖĆ ╬▓ņØś ņČöņĀĢņŗØņØä ņĢäļלņÖĆ Ļ░ÖņØ┤ ņ£ĀļÅäĒĢĀ ņłś ņ׳ļŗż.
ņ£ä ļ▓ĀĒāĆļČäĒżļŖö 0Ļ│╝ 1 ņé¼ņØ┤ņØś ĒÖĢļźĀļ│Ćņłś xņŚÉ ļīĆĒĢśņŚ¼ ņ£ĀļÅäļÉśņŚłņ£╝ļéś ĒÖĢļźĀļ│ĆņłśņØś ņāüŌŗģĒĢś ĒĢ£Ļ│äņŚÉ ļö░ļØ╝ ļ▓öņ£äļź╝ ĒÖĢņןĒĢśĻ▒░ļéś ņČĢņåīĒĢĀ ņłś ņ׳ļŗż. ņ”ē, ļ▓ĀĒāĆļČäĒżļź╝ ļö░ļź┤Ļ│Ā ļ▓öņ£äĻ░Ć c<x<dņØĖ ĒÖĢļźĀļ│Ćņłś xņØś ĒÅēĻĘĀĻ│╝ ļČäņé░ņØĆ Eqs. (8) - (9)ņŗØĻ│╝ Ļ░ÖņØ┤ ļ│ĆĒśĢļÉ£ļŗż.
ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö ļ▓ĀĒāĆļČäĒżļź╝ ĻĖ░ļ░śņ£╝ļĪ£ Ļ░ĢņÜ░ņØś ņØ┤ļÅÖņØä ļ¬©ņØśĒĢśĻ│Ā Ļ░ĢņÜ░ ņĢÖņāüļĖö ļ®żļ▓äļź╝ ņāØņä▒ĒĢśņśĆļŗż. Ļ░ĢņÜ░ ņØ┤ļÅÖ ļ¬©ņØśņŚÉļŖö ĒŖ╣ņä▒ļ░®Ē¢źņØä ņØ┤ņÜ®ĒĢśņśĆļŗż. Ļ░ü Ļ▓®ņ×Éļ│ä ĒŖ╣ņä▒ļ░®Ē¢źņØĆ ļ▓ĀĒāĆļČäĒżļź╝ ĒåĄĒĢ┤ ņĀĢļ¤ēĒÖöļÉśļŖöļŹ░, ĻĘĖ ĒÅēĻĘĀņ£╝ļĪ£ļŖö Ļ▓®ņ×Éļ│äļĪ£ Ļ┤ĆņĖĪļÉ£ ņØ┤ļÅÖļ░®Ē¢źņØś ļīĆĒæ»Ļ░ÆņØä ņĀüņÜ®ĒĢśņśĆĻ│Ā, ļČäņé░ņØĆ Ļ▓®ņ×Éļ│äļĪ£ ņé░ņĀĢļÉ£ ĒÅēĻĘĀ ņØ┤ļÅÖļ░®Ē¢źņŚÉ ļīĆĒĢ£ ļ│ĆļÅÖņä▒ņØä ņ¢╝ļ¦łļéś ļ░śņśüĒĢĀņ¦ĆņŚÉ ĻĘ╝Ļ▒░ĒĢśņŚ¼ Ļ▓░ņĀĢĒĢśņśĆļŗż. ņØ┤ļŖö Ļ▓®ņ×Éļ│ä ĒÅēĻĘĀ ĒśĖņÜ░ļ░®Ē¢źņØĆ Ļ│ĄĻ░äņĀüņ£╝ļĪ£ ņØ╝Ļ┤ĆļÉ£ ĒŖ╣ņä▒ņØä ļ│┤ņØ┤ļŖöļŹ░ ļ░śĒĢ┤, ļČäņé░ņØĆ ņāüļīĆņĀüņ£╝ļĪ£ ņØ╝Ļ┤Ćņä▒ņØ┤ ļČĆņĪ▒Ē¢łĻĖ░ ļĢīļ¼ĖņØ┤ļŗż. ņČ®ļČäĒ׳ ļ¦ÄņØĆ ĒśĖņÜ░ņé¼ņāüņØś ļČäņäØņØä ĒåĄĒĢ┤ ņ¢┤ļŖÉ ņĀĢļÅä ņØ╝Ļ┤ĆļÉ£ ĒŖ╣ņä▒ņØ┤ ĒÖĢņØĖļÉ£ļŗżļ®┤ Ļ▓®ņ×Éļ│äļĪ£ ņČöņĀĢļÉ£ ļČäņé░ņØä ņé¼ņÜ®ĒĢśļŖö Ļ▓āļÅä Ļ░ĆļŖźĒĢĀ Ļ▓āņØ┤ļŗż. ņØ┤ļĀćĻ▓ī Ļ▓®ņ×Éļ│äļĪ£ Ļ▓░ņĀĢļÉ£ ļ▓ĀĒāĆļČäĒżļź╝ ņØ┤ņÜ®ĒĢśņŚ¼ ĒŖ╣ņä▒ļ░®Ē¢źņØś ļé£ņłśļź╝ ļ░£ņāØņŗ£Ēé©ļŗż. ļé£ņłśņØś ļ░£ņāØņŚÉļŖö Monte Carlo SimulationņØä ņØ┤ņÜ®ĒĢśņśĆļŗż. ļé£ņłśļ░£ņāØļÉ£ ĒŖ╣ņä▒ļ░®Ē¢źņØĆ 1ĒÜīņØś ļ¬©ņØś Ļ│╝ņĀĢ ļÅÖņĢł ļÅÖņØ╝ĒĢśĻ▓ī ņ£Āņ¦ĆļÉ£ļŗż. ļ¬©ņØśĻ░Ć ļüØļéśļ®┤ ĒŖ╣ņä▒ļ░®Ē¢źņØä ļŗżņŗ£ ļé£ņłśļ░£ņāØņŗ£ĒéżĻ│Ā ļŗżņŗ£ ļ¬©ņØśļź╝ ņ¦äĒ¢ēĒĢśĻ▓ī ļÉ£ļŗż. ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö ņØ┤ Ļ│╝ņĀĢņØä 100ĒÜī ļ░śļ│ĄĒĢśņśĆļŗż.
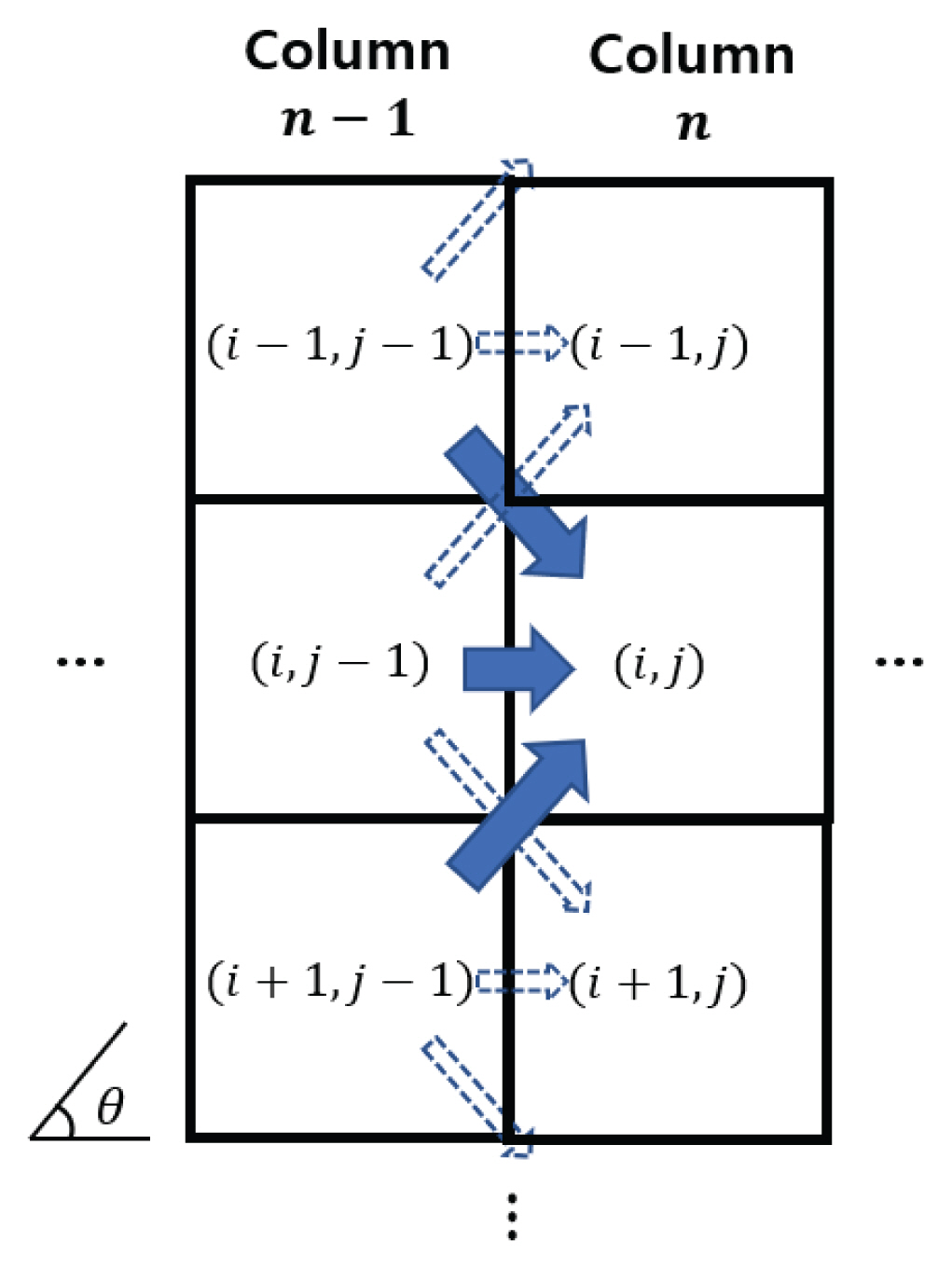
ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ņØś Ļ░ĢņÜ░ ņØ┤ļÅÖ ļ¬©ņØśĻ│╝ņĀĢņØä ĻĄ¼ņ▓┤ņĀüņ£╝ļĪ£ ņäżļ¬ģĒĢśļ®┤ ļŗżņØīĻ│╝ Ļ░Öļŗż. ņŚ¼ĻĖ░ņä£ļŖö ņØ┤ Ļ│╝ņĀĢņŚÉ ļīĆĒĢ£ ņØ┤ĒĢ┤ļź╝ ļÅĢĻĖ░ ņ£äĒĢ┤ Ļ░ĢņÜ░Ļ░Ć ņä£ņ¬ĮņŚÉņä£ ļÅÖņ¬Įņ£╝ļĪ£ ņØ┤ļÅÖĒĢ£ļŗżĻ│Ā Ļ░ĆņĀĢĒĢśņśĆļŗż. ļö░ļØ╝ņä£ ņÖ╝ņ¬Į ņŚ┤ņØś ļ¬©ņØś Ļ▓░Ļ│╝ļŖö ņśżļźĖņ¬Į ņŚ┤ņŚÉņä£ņØś ļ¬©ņØś Ļ│╝ņĀĢņØś ņ×ģļĀźņ×ÉļŻīļĪ£ ņé¼ņÜ®ļÉ£ļŗż. ĻĘĖļ”¼Ļ│Ā ļ¦żņŗ£Ļ░ä ļŗ©ņ£äļ¦łļŗż ņ×ģļĀźĻ░ĢņÜ░Ļ░Ć ĒĢ£ Ļ▓®ņ×Éņö® ņøĆņ¦üņØ┤ļŖöļŹ░ ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö ņØ┤ Ļ│╝ņĀĢņØä ŌĆ£stepŌĆØņØ┤ļØ╝Ļ│Ā ļČĆļźĖļŗż. ņ×ģļĀźĻ░ĢņÜ░ņןņØ┤ ļ¦ż stepļ¦łļŗż ņÖ╝ņ¬Į ņŚ┤ņŚÉņä£ ņśżļźĖņ¬Į ņŚ┤ļĪ£ĒĢ£ ļŗ©Ļ│äņö® ņØ┤ļÅÖĒĢśļ®░, ņ×ģļĀźĻ░ĢņÜ░ņןņØ┤ ļīĆņāü ņśüņŚŁņØä ļ¬©ļæÉ ļ╣ĀņĀĖļéśĻ░Ćļ®┤ 1ĒÜī ļ¬©ņØśĻ░Ć ņóģļŻīļÉ£ļŗż. Fig. 1ņØĆ Ļ▓®ņ×Éļ│ä Ļ░ĢņÜ░Ļ░ĢļÅäĻ░Ć ņĀäņØ┤ļÉśļŖö Ļ▓ĮļĪ£ļź╝ ļéśĒāĆļéĖ Ļ▓āņØ┤ļŗż. n-1 ņŚ┤ņØś Ļ▓®ņ×Éļ│ä Ļ░ĢņÜ░Ļ░ĢļÅäļŖö n ņŚ┤ļĪ£ ņĀäņØ┤ļÉśļŖöļŹ░, ņØ┤ļĢī beta ╬Ė ņŚÉ ļö░ļØ╝ ļČäĒĢĀļÉ£ļŗż. beta ╬Ėļ×Ć, ļ¼┤ņ×æņ£äņä▒ņØ┤ ļČĆņŚ¼ļÉ£ Ļ▓®ņ×Éļ│ä ĒŖ╣ņä▒ļ░®Ē¢źņØä ņØśļ»ĖĒĢ£ļŗż. ņ”ē, n-1 ņŚ┤ (i, j-1) Ļ▓®ņ×ÉņØś Ļ░ĢņÜ░Ļ░ĢļÅäļŖö ĒĢ┤ļŗ╣ Ļ▓®ņ×ÉņØś betaņŚÉ ļö░ļØ╝ (i-1, j), (i, j), (i+1, j) Ļ▓®ņ×ÉļĪ£ ļČäĒĢĀļÉśņ¢┤ ņĀäņØ┤ļÉ£ļŗż. ļ░śļīĆļĪ£ n ņŚ┤ (i, j) Ļ▓®ņ×ÉņØś ņĄ£ņóģ Ļ░ĢņÜ░Ļ░ĢļÅäļŖö (i, j) Ļ▓®ņ×ÉļĪ£ Ļ░ĢņÜ░Ļ░ĢļÅäļź╝ ņĀäņØ┤ĒĢĀ ņłś ņ׳ļŖö n-1 ņŚ┤ņØś Ļ▓®ņ×Éļōż((i-1, j-1), (i, j-1), (i+1, j-1))ņŚÉņä£ ļČäļ”¼ ĒĢĀļŗ╣ļÉśļŖö Ļ░ĢņÜ░Ļ░ĢļÅäļź╝ ĒĢ®ņé░ĒĢśņŚ¼ Ļ▓░ņĀĢļÉ£ļŗż. Table 1ņØĆ (i, j) Ļ▓®ņ×ÉļĪ£ Ļ▓░ĒĢ®ļÉśļŖö Ļ░ĢņÜ░Ļ░ĢļÅäņØś ņŚ¼ļ¤¼ Ļ▓ĮņÜ░ļź╝ ņĀĢļ”¼ĒĢ£ Ļ▓āņØ┤ļŗż. ņØ┤ņĀä ņŚ┤ Ļ▓®ņ×ÉņØś beta ╬Ė Ļ░Ć 0┬░ļ│┤ļŗż Ēü░ņ¦Ć Ēś╣ņØĆ ņ×æņØĆņ¦ĆņŚÉ ļö░ļØ╝ ļŗżņØī ņŚ┤ļĪ£ ĒĢĀļŗ╣ļÉśļŖö Ļ▓®ņ×ÉĻ░Ć ļŗ¼ļØ╝ņ¦ĆĻ▓īļÉśļ®░, ņØ┤ļĢī ņĀäņØ┤ļÉśļŖö Ļ░ĢņÜ░Ļ░ĢļÅäņØś Ēü¼ĻĖ░ļŖö beta ╬Ė ņŚÉ ļīĆĒĢ£ cos╬Ė Ļ░ÆĻ│╝ sin╬Ė Ļ░ÆņŚÉ ļö░ļØ╝ Ļ▓░ņĀĢļÉ£ļŗż.
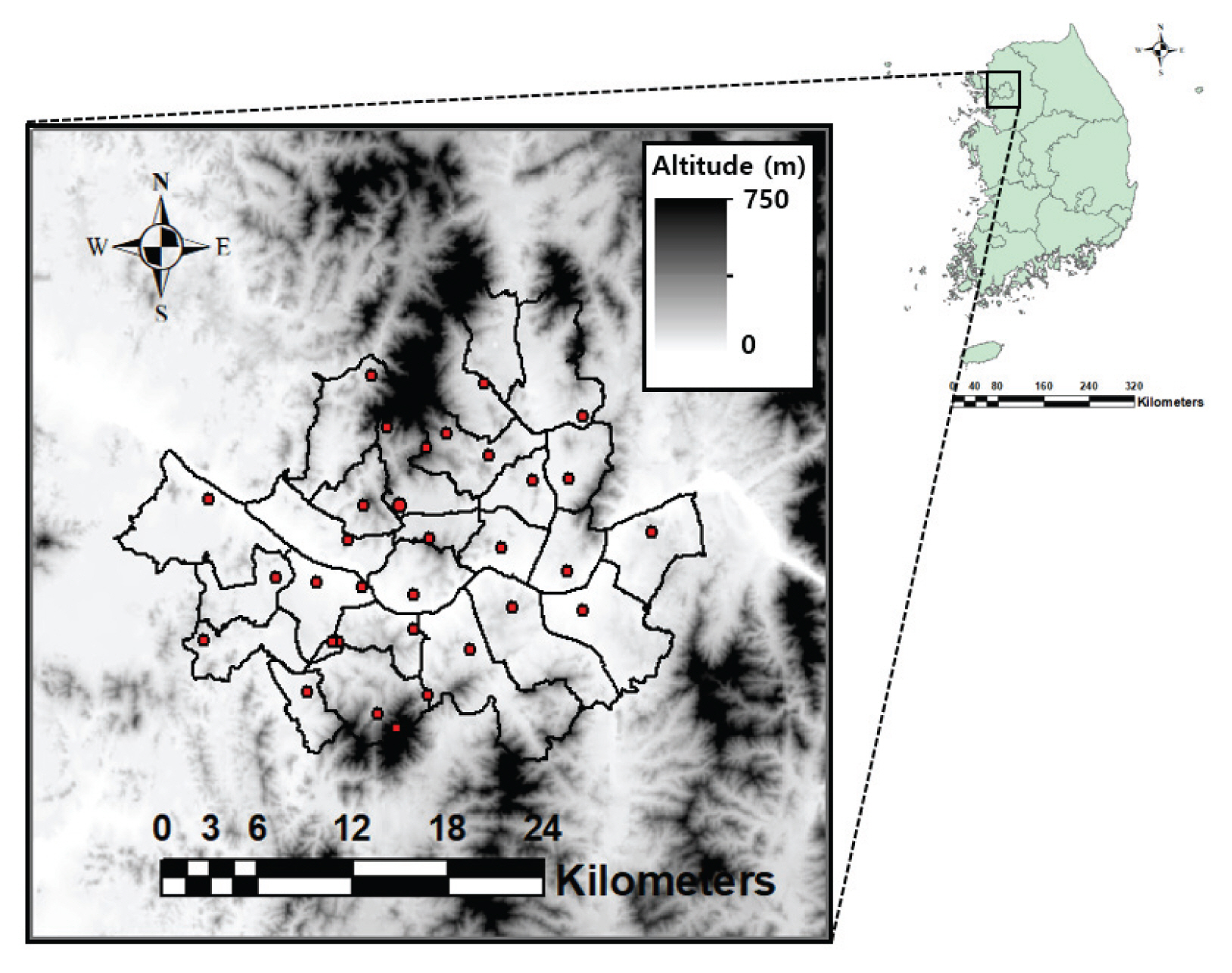
ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö ņä£ņÜĖĒŖ╣ļ│äņŗ£ļź╝ ļīĆņāüņ£╝ļĪ£ ĒĢśņŚ¼ Ļ░ĢņÜ░ ņĢÖņāüļĖö ļ®żļ▓ä ņāØņä▒ ĻĖ░ļ▓ĢņØä ņĀüņÜ®ĒĢśņśĆļŗż. ņä£ņÜĖĒŖ╣ļ│äņŗ£ļŖö ņÜ░ļ”¼ļéśļØ╝ņØś ņłśļÅäļĪ£ņŹ©, ņżæļČĆņ¦ĆņŚŁņŚÉ ņ£äņ╣śĒĢśļ®░ ņä£ĒĢ┤ņĢłņŚÉ ņØĖņĀæĒĢ£ ļīĆļÅäņŗ£ņØ┤ļŗż. ņä£ņÜĖĒŖ╣ļ│äņŗ£ņØś ļ®┤ņĀüņØĆ ņĢĮ 600 km2ņØ┤ļ®░, ņżæņŗ¼ļČĆņŚÉļŖö ĒĢ£Ļ░Ģ ļ│ĖļźśĻ░Ć ļÅÖņ¬ĮņŚÉņä£ ņä£ņ¬Įņ£╝ļĪ£ ĒØÉļź┤Ļ│Ā ņ׳Ļ│Ā, ļČüņ¬ĮņŚÉļŖö ļČüĒĢ£ņé░ņØ┤, ļé©ņ¬ĮņŚÉļŖö Ļ┤ĆņĢģņé░ņØ┤ ņ£äņ╣śĒĢ┤ ņ׳ļŗż. ļČüĒĢ£ņé░ņØĆ ļé©ļČüļ░®Ē¢źņ£╝ļĪ£ ļ╗Śņ¢┤ņ׳Ļ│Ā, Ļ┤ĆņĢģņé░ņØĆ ļÅÖņä£ļ░®Ē¢źņ£╝ļĪ£ ļ╗Śņ¢┤ ņ׳ņ£╝ļ®░, ĻĘĖ ņé¼ņØ┤ļĪ£ ĒĢ£Ļ░ĢņØ┤ ĒØÉļź┤Ļ│Ā ņ׳ļŗż. ņØ┤ļ¤¼ĒĢ£ ņ¦ĆĒśĢņĀüņØĖ ĒŖ╣ņä▒ņØĆ ņä£ņÜĖĒŖ╣ļ│äņŗ£ ņżæņŗ¼ļČĆņŚÉ ņ¦ĆĒśĢņĀüņØĖ ņłśļĀ┤ļīĆ(convergence area)ļź╝ ļ¦īļōżĻ▓ī ļÉ£ļŗż. ĒŖ╣Ē׳ ņä£ņ¬ĮņŚÉņä£ ņ£Āņ×ģļÉśļŖö ļīĆļźśņä▒ ĒśĖņÜ░ņé¼ņāüņØĆ ņłśļĀ┤ļīĆĻ░Ć ĒśĢņä▒ļÉśļŖö ņä£ņÜĖĒŖ╣ļ│äņŗ£ņØś ņżæņŗ¼ļČĆņŚÉņä£ Ļ░ĢņÜ░Ļ░ĢļÅäĻ░Ć ņ╗żņ¦ĆļŖö ĒŖ╣ņä▒ņØä ļ│┤ņØ╝ Ļ░ĆļŖźņä▒ņØ┤ Ēü¼ļŗż. ņØ┤ļ¤¼ĒĢ£ ņä£ņÜĖĒŖ╣ļ│äņŗ£ņØś ņ¦ĆĒśĢņĀü ĒŖ╣ņä▒ņØĆ Fig. 2ņŚÉņä£ ĒÖĢņØĖĒĢĀ ņłś ņ׳ļŗż.
Ēśäņ×¼ ņä£ņÜĖĒŖ╣ļ│äņŗ£ ļé┤ņŚÉņä£ ņÜ┤ņśüļÉśĻ│Ā ņ׳ļŖö ļ░®ņ×¼ĻĖ░ņāüĻ┤ĆņĖĪņןļ╣ä(AWS)ļŖö ņ┤Ø 32Ļ░£ņØ┤ļ®░, ņóģĻ┤ĆĻĖ░ņāüĻ┤ĆņĖĪņןļ╣ä(ASOS)ļŖö 1Ļ░£ņØ┤ļŗż. ņØ┤ļōż ņןļ╣ä(ņ”ē, ņ¦ĆņāüĻ┤ĆņĖĪņåī)ļŖö ņä£ņÜĖ ņĀäņŚŁņŚÉ ļ╣äĻĄÉņĀü ĻĘĀņ¦łĒĢśĻ▓ī ļČäĒżļÉśņ¢┤ ņ׳ļŗż(Fig. 2). AWSņÖĆ ASOSņŚÉņä£ļŖö 1ļČä Ļ░ĢņÜ░ Ļ┤ĆņĖĪņ×ÉļŻīļź╝ ņĀ£Ļ│ĄĒĢśĻ│Ā ņ׳ņ£╝ļéś, ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö Ļ│äņé░ņŗ£Ļ░äņØä ņżäņØ┤ĻĖ░ ņ£äĒĢ┤ ļČäļŗ©ņ£ä Ļ░ĢņÜ░ņ×ÉļŻīļź╝ 10ļČäļŗ©ņ£ä Ļ░ĢņÜ░ņ×ÉļŻīļĪ£ ļ│ĆĒÖśĒĢśņŚ¼ ņØ┤ņÜ®ĒĢśņśĆļŗż.
ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö ņĄ£ĻĘ╝ 10ļģä ļÅÖņĢł ņä£ņÜĖĒŖ╣ļ│äņŗ£ņŚÉņä£ ļ░£ņāØĒĢ£ ņŻ╝ņÜö ĒśĖņÜ░ņé¼ņāü ņ×ÉļŻīļź╝ ņØ┤ņÜ®ĒĢśņśĆļŗż. ņŻ╝ņÜö ĒśĖņÜ░ņé¼ņāüņØĆ ņ┤Ø Ļ░ĢņÜ░ļ¤ēņØ┤ ņ¢┤ļŖÉ ņĀĢļÅä Ēü░ ĒśĖņÜ░ņé¼ņāüņØä ļ¦ÉĒĢ£ļŗż. 2009ļģäļČĆĒä░ 2018ļģäĻ╣īņ¦Ć ņ┤Ø 37Ļ░£ņØś ņŻ╝ņÜö ĒśĖņÜ░ņé¼ņāüņØä ņäĀļ│äĒĢśņśĆņ£╝ļ®░, ļ░£ņāØ ņØ╝ņ×ÉņÖĆ ņ┤Ø Ļ░ĢņÜ░ļ¤ēņØĆ Table 2ņŚÉ ņĀĢļ”¼ĒĢśņśĆļŗż. ĒśĖņÜ░ņé¼ņāü ņżæ Ļ░Ćņן ĻĘ£ļ¬©Ļ░Ć Ēü░ Ļ▓āņØĆ 2011ļģä 7ņøö 26ņØ╝ļČĆĒä░ 28ņØ╝ņŚÉ ļ░£ņāØĒĢ£ ņ¦æņżæĒśĖņÜ░ņśĆļŗż. 3ņØ╝Ļ░ä ņ┤Ø 587.0 mmņØś ļ╣äĻ░Ć ļé┤ļĀĖņ£╝ļ®░, ņØ┤ļŖö ņä£ņÜĖĒŖ╣ļ│äņŗ£ņŚÉņä£ ļ░£ņāØĒĢ£ 3ņØ╝ ņŚ░ņåŹ Ļ░Ģņłśļ¤ē ņżæ 1907ļģä ĻĖ░ņāü Ļ┤ĆņĖĪ ņØ┤ļל ņŚŁļīĆ ņĄ£ļīĆ ĻĘ£ļ¬©ņśĆļŗż(KMA, 2011). ĒŖ╣Ē׳ Ļ┤ĆņĢģĻ┤ĆņĖĪņåīņŚÉņä£ 27ņØ╝ 8ņŗ£ņŚÉ Ļ┤ĆņĖĪļÉ£ Ļ░ĢņÜ░Ļ░ĢļÅäļŖö 110.5 mm/hrļĪ£ Ļ┤ĆņĖĪ ņŗ£ņ×æ ņØ┤ļל ņĄ£ļīĆņ╣śļź╝ ĻĖ░ļĪØĒ¢łļŗż. ļśÉĒĢ£, ņä£ņ┤łĻĄ¼ņŚÉ ņ£äņ╣śĒĢ£ ņÜ░ļ®┤ņé░ ņØ╝ļīĆņŚÉ ņé░ņé¼Ēā£Ļ░Ć ļ░£ņāØĒĢśĻ│Ā, Ļ░Ģļé©ņŚŁĻ│╝ ļīĆņ╣śļÅÖ ņé¼Ļ▒░ļ”¼ ļō▒ņØ┤ ņ╣©ņłśļÉśļŖö ļō▒ ņØĖļ¬ģ, ņ×¼ņé░ Ēö╝ĒĢ┤Ļ░Ć ļ░£ņāØĒĢśņśĆļŗż. 2010ļģä 9ņøö 21ņØ╝ņŚÉļÅä Ēā£ĒÆŹ ļ¦ÉļØ╝ņ╣┤ņŖżņØś ņśüĒ¢źņ£╝ļĪ£ ņżæļČĆņ¦Ćļ░®ņŚÉ Ēü░ ļ╣äĻ░Ć ļé┤ļĀż Ļ┤æĒÖöļ¼Ė ņØ╝ļīĆĻ░Ć ņ╣©ņłśļÉśņŚłļŗż(KMA, 2010). ĒĢ£ĒÄĖ 2010ļģä 6ņøö 12ņØ╝Ļ│╝ 2018ļģä 6ņøö 26ņØ╝ņŚÉ ļ░£ņāØĒĢ£ ĒśĖņÜ░ņé¼ņāüĻ│╝ Ļ░ÖņØ┤ ņĄ£ļīĆĻ░ĢņÜ░Ļ░ĢļÅäĻ░Ć ņĢĮ 20 mm/hr ņĀĢļÅäņŚÉ ļČłĻ│╝ĒĢ£ ĒśĖņÜ░ņé¼ņāüļÅä ņ׳ļŗż. ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ Ļ│ĀļĀżĒĢ£ ĒśĖņÜ░ņé¼ņāüņØĆ ĻĘ£ļ¬©ņŚÉ Ļ┤ĆĻ│äņŚåņØ┤ ļīĆļČĆļČä ņä£ņÜĖņØś ņä£ņ¬ĮņŚÉņä£ ļÅÖņ¬Įņ£╝ļĪ£ ņØ┤ļÅÖĒĢśļŖö Ļ▓ĮĒ¢źņØä ļéśĒāĆļé┤Ļ│Ā ņ׳ļŗż.
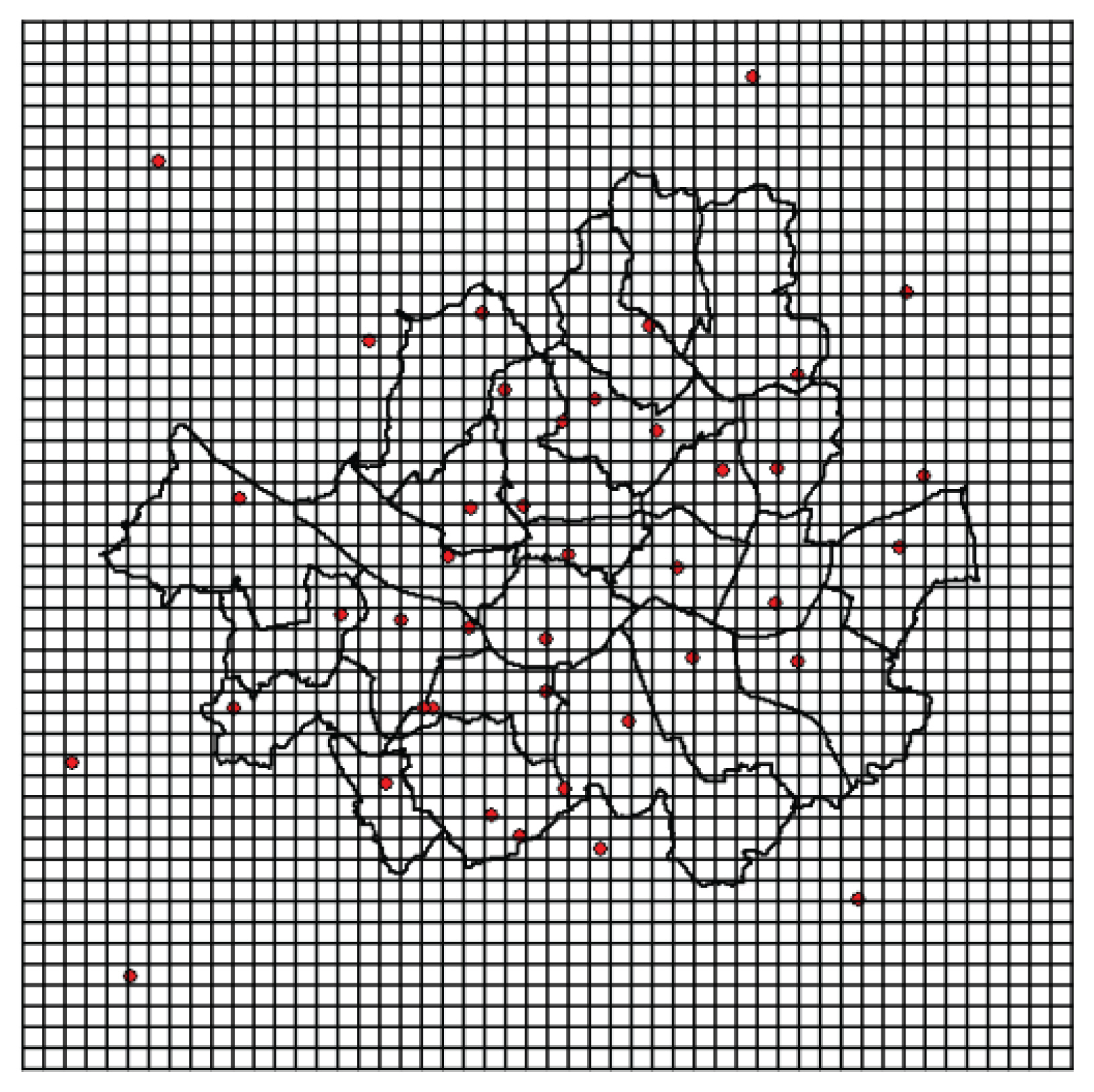
ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö ņ¦ĆņŚŁĒŖ╣ņä▒ Ļ░Ćņżæņ╣śļź╝ Ļ▓░ņĀĢĒĢśĻĖ░ņŚÉ ņĢ×ņä£ ļ©╝ņĀĆ ņä£ņÜĖĻ│╝ ņŻ╝ļ│Ć ņ¦ĆņŚŁņØä ĒżĻ┤äĒĢśļŖö 50 ├Ś 50 km2 Ēü¼ĻĖ░ņØś ņĀĢņé¼Ļ░üĒśĢ ļ¬©ņØś Ļ▓®ņ×Éļ¦ØņØä ĻĄ¼ņČĢĒĢśņśĆļŗż. ļŗ©ņ£äĻ▓®ņ×ÉņØś Ēü¼ĻĖ░ļŖö 1├Ś1 km2ņØ┤ļ®░, ņ┤Ø 50 ├Ś 50Ļ░£ņØś Ļ▓®ņ×ÉļĪ£ ĻĄ¼ņä▒ļÉśņŚłļŗż(Fig. 3). ņØ┤ Ļ▓®ņ×Éļ¦ØņØĆ Ļ░ĢņÜ░ņØś ņØ┤ļÅÖņØä ņĀüņĀłĒĢśĻ▓ī ļ¬©ņØśĒĢĀ ņĀĢļÅäņØś Ļ│ĄĻ░äĒĢ┤ņāüļÅäļź╝ Ļ░¢ņČś Ļ▓āņ£╝ļĪ£ ĒīÉļŗ©ĒĢśņśĆļŗż. ļ¬©ņØś Ļ│╝ņĀĢņŚÉņä£ļÅä ļ¼ĖņĀ£Ļ░Ć ņŚåņŚłļŗż.
Fig. 3ņØś Ļ▓®ņ×Éļ¦ØņŚÉļŖö ņ¦ĆņŚŁĒŖ╣ņä▒ Ļ░Ćņżæņ╣śņØś ņ£ĀļÅäļź╝ ņ£äĒĢ┤ ņé¼ņÜ®ĒĢ£ ņ¦ĆņāüĻ┤ĆņĖĪņåīņØś ņ£äņ╣śĻ░Ć ņżæņ▓®ļÉśņ¢┤ Ēæ£ņŗ£ļÉśņ¢┤ ņ׳ļŗż. ņØ┤ ĻĘĖļ”╝ņŚÉņä£ ĒÖĢņØĖĒĢĀ ņłś ņ׳ļō»ņØ┤ ņä£ņÜĖ ņ¦ĆņŚŁņŚÉļŖö ņ¦ĆņāüĻ┤ĆņĖĪņåīĻ░Ć ļ░ĆļÅäņ׳Ļ▓ī Ļ│ĀļŻ© ļČäĒżļÉśņ¢┤ņ׳ņ£╝ļéś, ņä£ņÜĖņØś ņÖĖĻ│Į ņ¦ĆņŚŁņŚÉļŖö ņ¦ĆņāüĻ┤ĆņĖĪņåīĻ░Ć ļŗżņåī ņä▒ĻĘ╝ Ļ│ĄĻ░äļ░ĆļÅäļź╝ ļ│┤ņØĖļŗż. ļö░ļØ╝ņä£ ņä£ņÜĖ ņÖĖĻ│Į ņ¦ĆņŚŁņŚÉņä£ ņ£ĀļÅäļÉ£ ņ¦ĆņŚŁĒŖ╣ņä▒ Ļ░Ćņżæņ╣śļŖö ņä£ņÜĖ ļé┤ļČĆņŚÉņä£ ļ│┤ļŗż ņĀĢļÅäĻ░Ć ļ¢©ņ¢┤ņ¦ł Ļ░ĆļŖźņä▒ņØ┤ Ēü░ Ļ▓āņØ┤ ņé¼ņŗżņØ┤ļŗż. ĻĘĖļ¤¼ļéś ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö ņĄ£ņóģņĀüņ£╝ļĪ£ ņ£ĀļÅäļÉśļŖö ņ¦ĆņŚŁĒŖ╣ņä▒ Ļ░Ćņżæņ╣śņØś ņĀĢļÅäļŖö Ļ░ÖļŗżĻ│Ā Ļ░ĆņĀĢĒĢśĻ│Ā ņŚ░ĻĄ¼ļź╝ ņ¦äĒ¢ēĒĢśņśĆļŗż. ņ¦ĆņāüĻ┤ĆņĖĪņåīĻ░Ć ņ£äņ╣śĒĢśņ¦Ć ņĢŖļŖö Ļ▓®ņ×ÉņŚÉņä£ņØś ņ¦ĆņŚŁĒŖ╣ņä▒ Ļ░Ćņżæņ╣śļŖö ņŚŁĻ▒░ļ”¼Ļ░Ćņżæļ▓ĢņØä ĒåĄĒĢ┤ ņ£ĀļÅäļÉśņŚłļŗż.
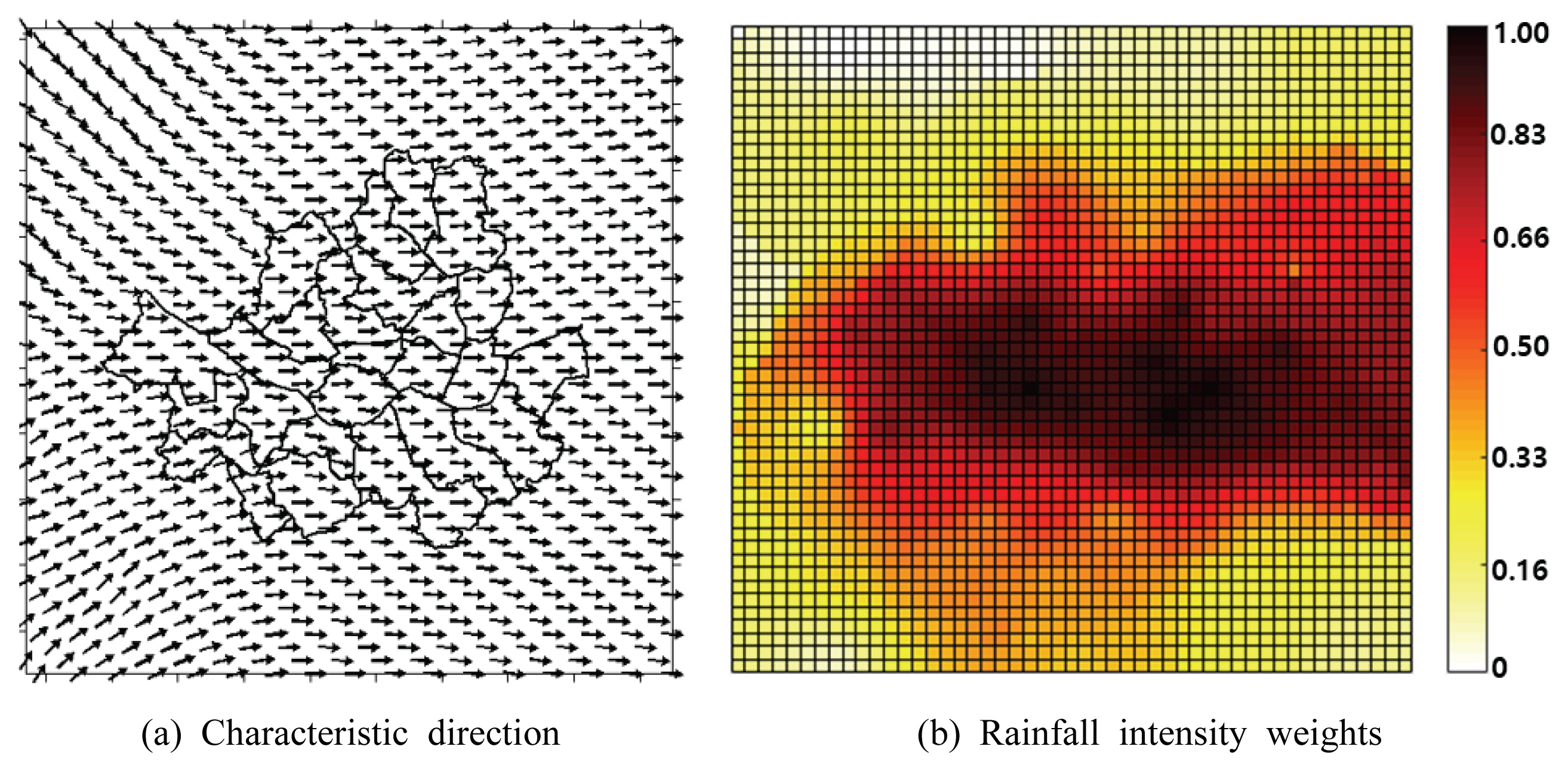
ĻĄ¼ņČĢļÉ£ ļ¬©ņØś Ļ▓®ņ×Éļ¦ØņØä ĻĖ░ļ░śņ£╝ļĪ£ ĒŖ╣ņä▒ļ░®Ē¢źņØä Ļ▓░ņĀĢĒĢśņśĆļŗż. 2009ļģäļČĆĒä░ 2018ļģäĻ╣īņ¦Ć ļ░£ņāØĒĢ£ ņŻ╝ņÜö ĒśĖņÜ░ņé¼ņāü ņ×ÉļŻīļź╝ ņØ┤ņÜ®ĒĢśņśĆņ£╝ļ®░, ņØ╝ļĀ©ņØś ļČäņäØĻ│╝ņĀĢņØä Ļ▒░ņ│É 50 ├Ś 50Ļ░£ Ļ▓®ņ×ÉņŚÉ ļīĆĒĢ┤ ĒŖ╣ņä▒ļ░®Ē¢źņØä Ļ▓░ņĀĢĒĢśņśĆļŗż. ņĄ£ņóģņĀüņ£╝ļĪ£ Ļ▓░ņĀĢļÉ£ ĒŖ╣ņä▒ļ░®Ē¢źņØĆ Fig. 4(a)ņÖĆ Ļ░Öļŗż. ĒŖ╣ņä▒ļ░®Ē¢źņØ┤ ņĀäņ▓┤ņĀüņ£╝ļĪ£ ņä£ņ¬ĮņŚÉņä£ ļÅÖņ¬ĮņØä Ļ░Ćļ”¼Ēéżļ®░, ņżæņĢÖņŚÉ ņ¦æņżæļÉśļŖö ĒśĢĒā£ļź╝ ļ│┤ņØĖļŗż. ņØ┤ļŖö ņä£ņÜĖĒŖ╣ļ│äņŗ£ņØś ņ¦ĆĒśĢĒĢÖņĀü, ĻĖ░ĒøäĒĢÖņĀü ĒŖ╣ņä▒ņØ┤ ĒŖ╣ņä▒ļ░®Ē¢źņŚÉ ļ░śņśüļÉśņŚłĻĖ░ ļĢīļ¼Ėņ£╝ļĪ£ ĒĢ┤ņäØĒĢĀ ņłś ņ׳ļŗż. Ļ│╝Ļ▒░ņŚÉ ņä£ņÜĖĒŖ╣ļ│äņŗ£ņŚÉņä£ ļ░£ņāØĒĢ£ ņŻ╝ņÜö ĒśĖņÜ░ņé¼ņāüļōżņØĆ ļīĆļČĆļČä ņä£ņ¬ĮņŚÉņä£ ļÅÖņ¬Įņ£╝ļĪ£ ņØ┤ļÅÖĒĢśņśĆļŗż. ļśÉĒĢ£, ņä£ņÜĖĒŖ╣ļ│äņŗ£ņØś ļČüņ¬ĮĻ│╝ ļé©ņ¬ĮņŚÉļŖö Ļ░üĻ░ü ļČüĒĢ£ņé░Ļ│╝ Ļ┤ĆņĢģņé░ņØ┤ ņ£äņ╣śĒĢśņŚ¼ ĒśĖņÜ░Ļ░Ć ņä£ņ¬ĮņŚÉņä£ ļÅÖņ¬Įņ£╝ļĪ£ ņØ┤ļÅÖĒĢśļ®┤ ņä£ņÜĖņØś ņżæņĢÖļČĆļĪ£ ĒśĖņÜ░ņé¼ņāüņØ┤ ņ¦æņżæļÉśļŖö ļō»ĒĢ£ Ļ▓ĮĒ¢źņØä ļ│┤ņØ┤Ļ▓ī ļÉ£ļŗż.
Ļ│╝Ļ▒░ņŚÉ ļ░£ņāØĒĢ£ ĒśĖņÜ░ņé¼ņāüņØś 10ļČä Ļ░ĢņÜ░ļ¤ē ņ×ÉļŻīļź╝ ņØ┤ņÜ®ĒĢśņŚ¼ Ļ░ĢņÜ░Ļ░ĢļÅä Ļ░Ćņżæņ╣śļź╝ Ļ▓░ņĀĢĒĢśņśĆļŗż. Fig. 4(b)ļŖö Ļ░ĢņÜ░Ļ░ĢļÅä Ļ░Ćņżæņ╣śņØś Ļ▓░ņĀĢ Ļ▓░Ļ│╝ļź╝ ļéśĒāĆļéĖ Ļ▓āņØ┤ļŗż. Ļ▓ĆņĀĢņāēņŚÉ Ļ░ĆĻ╣īņÜĖņłśļĪØ Ļ░Ćņżæņ╣śĻ░Ć 1Ļ│╝ ņ£Āņé¼ĒĢśļ®░, ĒĢśņ¢ĆņāēņŚÉ Ļ░ĆĻ╣īņÜĖņłśļĪØ 0ņŚÉ Ļ░ĆĻ╣Øļŗż. ļ¬©ņØś Ļ▓®ņ×Éļ¦ØņØś ņżæņĢÖņŚÉ ņ£äņ╣śĒĢ£ Ļ▓®ņ×ÉļōżņØś Ļ░ĢņÜ░Ļ░ĢļÅä Ļ░Ćņżæņ╣śĻ░Ć ļŗżļźĖ Ļ▓®ņ×ÉļōżņŚÉ ļ╣äĒĢ┤ ņāüļīĆņĀüņ£╝ļĪ£ Ēü¼Ļ▓ī Ļ▓░ņĀĢļÉśņŚłļŗż. ņØ┤ļŖö ĒśĖņÜ░ņé¼ņāüņØ┤ ņŻ╝ļĪ£ ņä£ņÜĖĒŖ╣ļ│äņŗ£ņØś ņżæņĢÖņØä ņ¦ĆļéśĻ░ĆļŖö Ļ▓ĮļĪ£ļĪ£ ņØ┤ļÅÖĒĢśļŖö Ļ▓ĮĒ¢źņØä ļ│┤ņśĆĻĖ░ ļĢīļ¼ĖņØ┤ļŗż. Ļ▓░Ļ│╝ņĀüņ£╝ļĪ£ Ļ▓®ņ×Éļ¦ØņØś ņāüļŗ©Ļ│╝ ĒĢśļŗ©ļČĆ Ļ▓®ņ×ÉņØś Ļ░Ćņżæņ╣śļŖö ņāüļīĆņĀüņ£╝ļĪ£ ņ×æĻ▓ī Ļ▓░ņĀĢļÉ£ ļ░śļ®┤ ņżæņĢÖņŚÉ ņ£äņ╣śĒĢ£ Ļ▓®ņ×ÉņØś Ļ░Ćņżæņ╣śļŖö Ēü¼Ļ▓ī Ļ▓░ņĀĢļÉśņŚłļŗż. ņĄ£ņóģņĀüņ£╝ļĪ£ Ļ▓░ņĀĢļÉ£ Ļ░ĢņÜ░Ļ░ĢļÅä Ļ░Ćņżæņ╣śļŖö ĒŖ╣ņä▒ļ░®Ē¢źņØś ņĀüņĀĢņä▒ņØä ĒīÉļŗ©ĒĢśļŖöļŹ░ ņØ┤ņÜ®ļÉ£ļŗż.
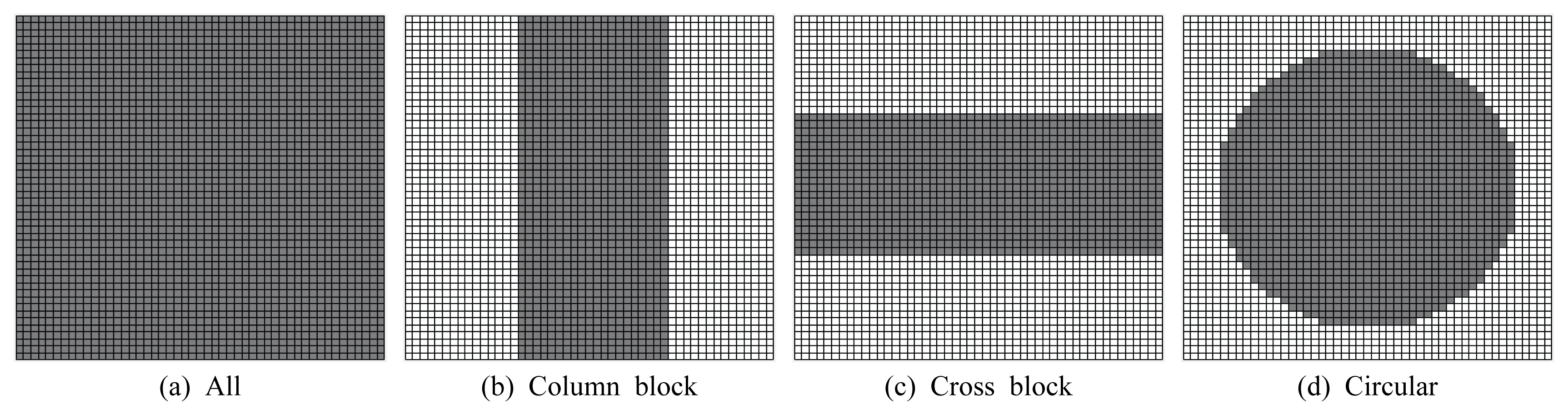
Ļ░ĢņÜ░ ņĢÖņāüļĖö ļ®żļ▓äļŖö ļ¬©ņØś Ļ▓®ņ×Éļ¦ØņŚÉ ņ×ģļĀźĻ░ĢņÜ░ņןņØ┤ ņØ┤ļÅÖ ļ¬©ņØśļÉ©ņ£╝ļĪ£ņŹ© ņāØņä▒ļÉ£ļŗż. ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö ļŗżņ¢æĒĢ£ ĒśĢĒā£ņØś ņ×ģļĀźĻ░ĢņÜ░ņןņØä Ļ│ĀļĀżĒĢśņśĆļŗż(Fig. 5). ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ Ļ▓ĆĒåĀĒĢ£ ņ×ģļĀźĻ░ĢņÜ░ņןņØĆ ņĀäņ▓┤ņŚÉ ļÅÖņØ╝ĒĢ£ Ļ░ĢņÜ░Ļ░ĢļÅäļź╝ ļČĆņŚ¼ĒĢ£ Ļ░ĢņÜ░ņן, ņäĖļĪ£ ļ¦ēļīĆĒśĢ, Ļ░ĆļĪ£ ļ¦ēļīĆĒśĢ, ņøÉĒśĢ Ļ░ĢņÜ░ņןņØ┤ļŗż. Ļ▓®ņ×Éļé┤ņŚÉ Ļ░ĢņÜ░Ļ░Ć ņ׳ļŖö Ļ▓ĮņÜ░ ĻĘĖ Ļ░ĢņÜ░Ļ░ĢļÅäļŖö 50 mm/hrņ£╝ļĪ£ ļÅÖņØ╝ĒĢśĻ▓ī ņäżņĀĢĒĢśņśĆļŗż. 4Ļ░Ćņ¦Ć ņ×ģļĀźĻ░ĢņÜ░ņןņØĆ Ļ▓®ņ×Éļ¦ØņØś ņÖ╝ņ¬ĮņŚÉņä£ ņ×ģļĀźļÉśņ¢┤ ņśżļźĖņ¬Į ļ░®Ē¢źņ£╝ļĪ£ ņØ┤ļÅÖ ļ¬©ņØśļÉ£ļŗż.
ĒŖ╣ņä▒ļ░®Ē¢źņØś ņśüĒ¢źļÅä ĒĢ©Ļ╗ś ņé┤ĒÄ┤ļ│┤ĻĖ░ ņ£äĒĢ┤ ĒŖ╣ņä▒ļ░®Ē¢źņØś ļ¼┤ņ×æņ£äņä▒ņØä ļæÉ Ļ░Ćņ¦Ć ļ░®ļ▓Ģņ£╝ļĪ£ ļŗżļź┤Ļ▓ī ļČĆņŚ¼ĒĢśņśĆļŗż(Fig. 6). ņØ┤ ĻĘĖļ”╝ņŚÉņä£ Case 1ņØĆ ļ▓ĀĒāĆļČäĒżņØś ļČäņé░ņØä Ļ▓®ņ×Éļ│ä ĒŖ╣ņä▒ļ░®Ē¢źņØś ņĄ£ļīĆĻ░ÆĻ│╝ ņĄ£ņåīĻ░ÆņØś ņ░©ņØ┤ļĪ£ ņäżņĀĢĒĢśņŚ¼ ļ¬©ņØś ļ░£ņāØņŗ£Ēé© ĒŖ╣ņä▒ļ░®Ē¢źņØ┤Ļ│Ā, Case 2ļŖö ļČäņé░ņØä Ļ▓®ņ×Éļ│ä ĒŖ╣ņä▒ļ░®Ē¢źņØś 90%ļź╝ ĒżĒĢ©ĒĢśļŖö ĻĄ¼Ļ░äņ£╝ļĪ£ ņäżņĀĢĒĢśņŚ¼ ļ¬©ņØś ļ░£ņāØņŗ£Ēé© ĒŖ╣ņä▒ļ░®Ē¢źņØ┤ļŗż. ņØ┤ ļæÉ Ļ▓ĮņÜ░ ļ¬©ļæÉ ņĀäņ▓┤ņĀüņØĖ ļ░®Ē¢źņØĆ Fig. 4(a)ņØś ĒŖ╣ņä▒ļ░®Ē¢źĻ│╝ ņØ╝ņ╣śĒĢśļéś ĻĘĖ ļ│ĆļÅÖņä▒ņØĆ Ēü¼Ļ▓ī ļŗżļźĖ Ļ▓āņØä ĒÖĢņØĖĒĢĀ ņłś ņ׳ļŗż.
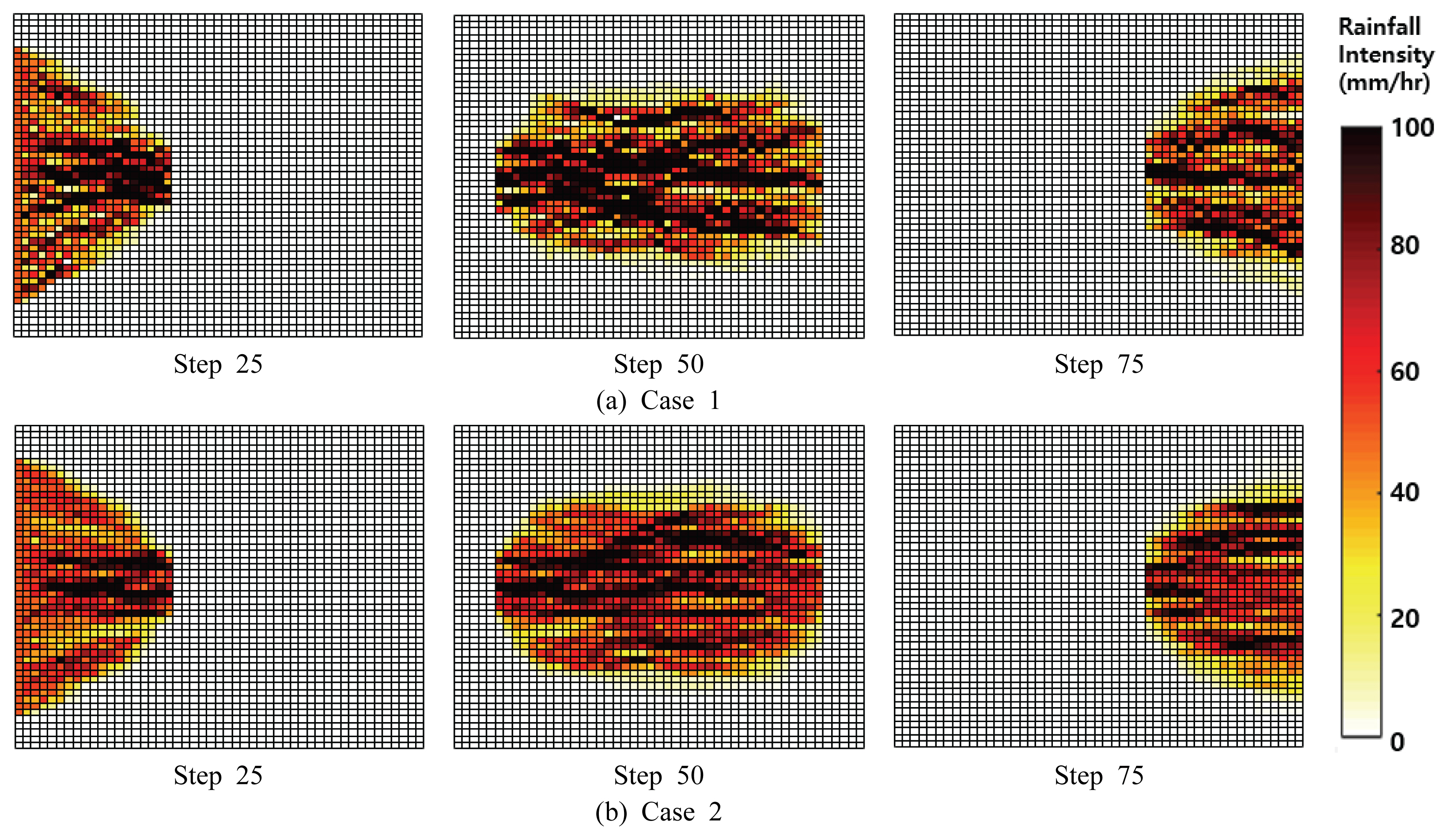
Figs. 7(a)ņÖĆ (b)ļŖö Ļ░üĻ░ü Case 1Ļ│╝ Case 2ņØś ņøÉĒśĢ ņ×ģļĀźĻ░ĢņÜ░ņןņŚÉ ļīĆĒĢ£ ņØ┤ļÅÖ ļ¬©ņØś Ļ│╝ņĀĢņØä ļ│┤ņŚ¼ņŻ╝Ļ│Ā ņ׳ļŗż. ņ”ē, Figs. 6(a)ņÖĆ (b)ņŚÉ Fig. 5(d)ļź╝ ņØ┤ļÅÖļ¬©ņØśņŗ£Ēé© Ļ▓░Ļ│╝ņØ┤ļŗż. ņ×ģļĀźĻ░ĢņÜ░ņןņØś Ēü¼ĻĖ░ļÅä ļ¬©ņØś Ļ▓®ņ×Éļ¦ØĻ│╝ ļÅÖņØ╝ĒĢśĻ▓ī 50 ├Ś 50ņØ┤ĻĖ░ ļĢīļ¼ĖņŚÉ step 50ņŚÉ ļ¬©ļōĀ ņ×ģļĀźĻ░ĢņÜ░Ļ░Ć Ļ▓®ņ×Éļ¦Ø ļé┤ļĪ£ ņ£Āņ×ģļÉ£ļŗż. Step 25ļŖö ņ£Āņ×ģļÉśļŖö ņ×ģļĀźĻ░ĢņÜ░ņןņØś ļ¬©ņŖĄņØä ļ│┤ņŚ¼ņżĆļŗż. Step 50ņŚÉņä£ļŖö ņ×ģļĀźĻ░ĢņÜ░ņןņØ┤ ņÖäņĀäĒ׳ ņ£Āņ×ģļÉśņ¢┤ ļ¬©ņØś Ļ▓®ņ×Éļ¦ØņØś ņżæņĢÖņŚÉ ņ£äņ╣śĒĢśĻ│Ā ņ׳ļŗż. Step 75ļŖö ņ×ģļĀźļÉ£ Ļ░ĢņÜ░ņןņØ┤ ņČ£ļĀźļÉśļŖö ļ¬©ņŖĄņØ┤ļŗż. Case 1Ļ│╝ 2ņŚÉņä£ ļ¬©ļæÉ ņ×ģļĀźļÉ£ Ļ░ĢņÜ░ņןņØ┤ ĒŖ╣ņä▒ļ░®Ē¢źņØś Ļ▓ĮĒ¢źņŚÉ ļö░ļØ╝ ņżæņĢÖļČĆļĪ£ ņ¦æņżæļÉśļŖö ĒśĢĒā£ļź╝ ļ│┤ņśĆļŗż. ņØ┤ļĢī Case 2(Fig. 7(b))ļ│┤ļŗż Case 1(Fig. 7(a))ņŚÉņä£ Ļ░ĢņÜ░Ļ░Ć ĒŖ╣ņĀĢ Ļ▓ĮļĪ£ņŚÉ ņ¦æņżæļÉśļŖö ĒśäņāüņØ┤ ļŹöņÜ▒ ļæÉļō£ļ¤¼ņ¦ĆĻ▓ī ļéśĒāĆļé¼ļŗż. ņØ┤ļŖö ļé£ņłśņØś ļ░£ņāØ ļ▓öņ£äĻ░Ć ĒŖ╣ņä▒ļ░®Ē¢źņØś ļ¼┤ņ×æņ£äņä▒ņŚÉ ņśüĒ¢źņØä ļ»Ėņ╣śĻĖ░ ļĢīļ¼ĖņØ┤ļŗż. ņ”ē, ļ¼┤ņ×æņ£äņä▒ņØ┤ ņ╗żņ¦łņłśļĪØ ņØ┤ņĀä ņŚ┤ņØś Ļ░ĢņÜ░Ļ░Ć ļŗżņØī ņŚ┤ļĪ£ ņĀäņØ┤ļÉĀ ļĢī ļŹö ĻĘ╣ļŗ©ņĀüņ£╝ļĪ£ ļČäĒĢĀļÉĀ Ļ░ĆļŖźņä▒ņØ┤ Ēü¼ĻĖ░ ļĢīļ¼ĖņŚÉ ļ¦łņ╣ś ĒŖ╣ņĀĢĒĢ£ Ļ▓ĮļĪ£ņŚÉ Ļ░ĢņÜ░Ļ░Ć ņ¦æņżæļÉśļŖö Ļ▓āņ▓śļ¤╝ ļ│┤ņØĖļŗż. ņ¦æņżæļÉ£ Ļ░ĢņÜ░ņןņØĆ ļ░Ćņ¦æļÉ£ ĒśĢĒā£Ļ░Ć ĻĘĖļīĆļĪ£ ņ£Āņ¦ĆļÉśļŖö ĒśĢĒā£ļĪ£ ņČ£ļĀźļÉśņŚłļŗż. ņØ┤ļ¤¼ĒĢ£ Ļ░ĢņÜ░ņØ┤ļÅÖ Ļ▓ĮĒ¢źņØĆ 100Ļ░£ņØś Ļ░ĢņÜ░ ņĢÖņāüļĖö ļ®żļ▓äņŚÉņä£ Ļ│ĄĒåĄņĀüņ£╝ļĪ£ ļéśĒāĆļé¼ļŗż.
ņŻ╝ņ¢┤ņ¦ä ņ×ģļĀźĻ░ĢņÜ░ņןņŚÉ ļīĆĒĢ┤ ņØ┤ļÅÖļ¬©ņØśļź╝ 100ĒÜī ņłśĒ¢ēĒĢśņŚ¼ ņ┤Ø 100Ļ░£ņØś Ļ░ĢņÜ░ ņĢÖņāüļĖö ļ®żļ▓äļź╝ ņāØņä▒ĒĢśņśĆļŗż. Fig. 8(a)ļŖö Case 1ņŚÉ ļīĆĒĢ┤ ņāØņä▒ĒĢ£ Ļ░ĢņÜ░ ņĢÖņāüļĖö ļ®żļ▓ä ņżæ 10, 40, 90ļ▓łņ¦Ė ļ®żļ▓äļōżņØś step 50ņŚÉņä£ņØś ļ¬©ņØś ņāüĒā£ļź╝ ļéśĒāĆļéĖ Ļ▓āņØ┤ļŗż. Fig. 8(b)ļŖö Case 2ņØś 25, 60, 75ļ▓łņ¦Ė ļ®żļ▓äņØ┤ļŗż. Step 50ņØĆ ņ×ģļĀźĻ░ĢņÜ░ņןņØ┤ ņÖäņĀäĒ׳ Ļ▓®ņ×Éļ¦Ø ļé┤ļĪ£ ņ£Āņ×ģļÉ£ ņāüĒā£ļź╝ ļéśĒāĆļéĖļŗż. Ļ░ĢņÜ░ ņØ┤ļÅÖ ļ¬©ņØśļŖö ļ▓ĀĒāĆļČäĒżļź╝ ņØ┤ņÜ®ĒĢśņŚ¼ ļ¬©ņØś ļ░£ņāØņŗ£Ēé© ļ¼┤ņ×æņ£äņĀüņØĖ ĒŖ╣ņä▒ļ░®Ē¢źņØä ĻĖ░ļ░śņ£╝ļĪ£ ņłśĒ¢ēļÉśļ»ĆļĪ£ ļ¬©ņØśļÉ£ Ļ░ĢņÜ░ ņĢÖņāüļĖö ļ®żļ▓äļŖö ļ¬©ļæÉ ļŗżļźĖ Ļ░ĢņÜ░Ļ░ĢļÅäļź╝ Ļ░Ćņ¦ĆĻ▓ī ļÉ£ļŗż. ĻĘĖ ņ░©ņØ┤ļŖö ļ¼╝ļĪĀ ļ¬©ņØśņŚÉ ņØ┤ņÜ®ĒĢ£ ĒŖ╣ņä▒ļ░®Ē¢ź ņ░©ņØ┤ņŚÉ ņØśĒĢ┤ Ļ▓░ņĀĢļÉ£ļŗż. ļé£ņłśļ░£ņāØ ļ▓öņ£äļź╝ Ļ▓®ņ×Éļ│ä ĒŖ╣ņä▒ļ░®Ē¢ź Ļ░Ćņżæņ╣śņØś ņĄ£ļīĆĻ░ÆĻ│╝ ņĄ£ņåīĻ░ÆņØś ņ░©ņØ┤ņŚÉ ĒĢ┤ļŗ╣ĒĢśļŖö ĻĄ¼Ļ░äņ£╝ļĪ£ ņäżņĀĢĒĢ£ Case 1ņØ┤ 90%ļź╝ ĒżĒĢ©ĒĢśļŖö ĻĄ¼Ļ░äņ£╝ļĪ£ ņäżņĀĢĒĢ£ Case 2ņŚÉ ļ╣äĒĢ┤ Ļ░ĢņÜ░Ļ░ĢļÅäņØś ļ¼┤ņ×æņ£äņä▒ņØ┤ ļŹö Ēü¼Ļ▓ī ļéśĒāĆļéśļŖö Ļ▓āņØĆ ļŗ╣ņŚ░ĒĢśļŗż. ļŗżļ¦ī, ņØ┤ļĢī ļé£ņłśļ░£ņāØņØś ļ▓öņ£äļŖö ņĀüņÜ® ļīĆņāü ņ¦ĆņŚŁ ļ░Å Ļ│╝Ļ▒░ ĒśĖņÜ░ņé¼ņāüņØś ĒŖ╣ņä▒ņŚÉ ļö░ļØ╝ ļŗżņ¢æĒĢśĻ▓ī ņĀüņÜ®ĒĢĀ ņłś ņ׳ļŗż.
ņØ┤ļÅÖļ¬©ņØśļÉ£ 100Ļ░£ņØś Ļ░ĢņÜ░ ņĢÖņāüļĖö ļ®żļ▓äņØś Ļ▓®ņ×Éļ│ä Ļ░ĢņÜ░Ļ░ĢļÅäļź╝ ĒÅēĻĘĀĒĢśļ®┤ Ļ░ĢņÜ░ ņĢÖņāüļĖö ĒÅēĻĘĀņØ┤ ņ£ĀļÅäļÉ£ļŗż. Figs. 9(a)ņÖĆ (b)ļŖö Ļ░üĻ░ü Case 1Ļ│╝ Case 2ņØś ņĀäņ▓┤, ņäĖļĪ£ ļ¦ēļīĆĒśĢ, Ļ░ĆļĪ£ ļ¦ēļīĆĒśĢ, ņøÉĒśĢ ņ×ģļĀźĻ░ĢņÜ░ņןņŚÉ ļīĆĒĢ£ step 50ņŚÉņä£ņØś Ļ░ĢņÜ░ ņĢÖņāüļĖö ĒÅēĻĘĀņØä ļéśĒāĆļéĖ Ļ▓āņØ┤ļŗż. ļ▓ĀĒāĆļČäĒżņØś ļČäņé░ņŚÉ ļö░ļźĖ Ļ░ĢņÜ░ ņĢÖņāüļĖö ĒÅēĻĘĀņØś ņ░©ņØ┤ļŖö ĻĘĖļ”¼ Ēü¼ņ¦Ć ņĢŖņØĆ Ļ▓āņ£╝ļĪ£ ļéśĒāĆļé¼ļŗż. Ļ░ĢņÜ░ ņĢÖņāüļĖö ĒÅēĻĘĀņØĆ Ļ░ĢņÜ░ ņĢÖņāüļĖö ļ®żļ▓ä 100Ļ░£ņØś ĒÅēĻĘĀņĀüņØĖ Ļ░ĢņÜ░Ļ░ĢļÅä ļČäĒżņØ┤ļ»ĆļĪ£ Ļ░ĢņÜ░ ņĢÖņāüļĖö ļ®żļ▓äņŚÉ ļ╣äĒĢ┤ ĒÅēĒÖ£ĒÖöļÉ£ Ļ░ĢņÜ░ņןņØś ĒśĢĒā£Ļ░Ć ņ£ĀļÅäļÉśņŚłļŗż. ļśÉĒĢ£, ņ×ģļĀźĻ░ĢņÜ░ņןņØś ĒśĢĒā£ņŚÉ Ļ┤ĆĻ│äņŚåņØ┤ Ļ│ĄĒåĄņĀüņ£╝ļĪ£ Ļ░ĢņÜ░Ļ░ĢļÅäĻ░Ć ļ¬©ņØś Ļ▓®ņ×Éļ¦ØņØś ņżæņĢÖļČĆņŚÉ ņ¦æņżæļÉśļŖö Ļ▓ĮĒ¢źņØ┤ ļéśĒāĆļé£ļŗż. ņØ┤ļŖö ņ×ģļĀź ņ┤łļ░śļČĆņŚÉ ņżæņĢÖļČĆļĪ£ ņ¦æņżæļÉśļŗżĻ░Ć ņ£Āņ¦ĆļÉśļ®┤ņä£ ņČ£ļĀźļÉśļŖö ĒŖ╣ņä▒ļ░®Ē¢ź Ļ░Ćņżæņ╣śņØś Ļ░ĢņÜ░ ņØ┤ļÅÖ ļ¬©ņØś ĒŖ╣ņä▒ņŚÉ ļö░ļźĖ Ļ▓░Ļ│╝ļĪ£ ĒĢ┤ņäØļÉ£ļŗż.
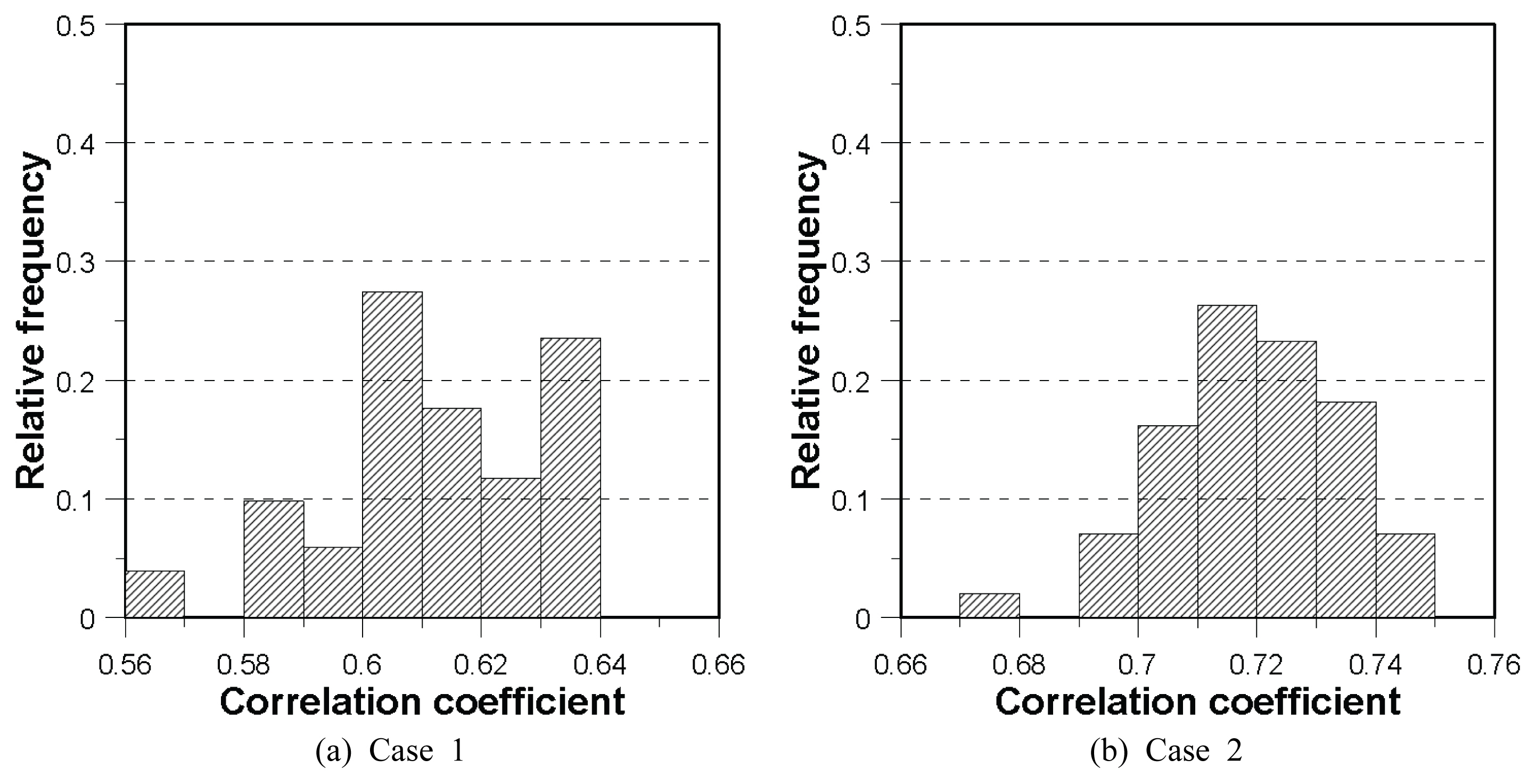
ņØ┤ņāüĻ│╝ Ļ░ÖņØ┤ ļ¬©ņØśļÉ£ Ļ░ĢņÜ░ ņĢÖņāüļĖö ļ®żļ▓äņØś ĒÅēĻ░Ćļź╝ ņ£äĒĢ┤ ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö Ļ░ĢņÜ░ ņĢÖņāüļĖö ļ®żļ▓äļź╝ Ļ░ĢņÜ░Ļ░ĢļÅä Ļ░Ćņżæņ╣śņÖĆ ļ╣äĻĄÉĒĢśņśĆļŗż. ĒŖ╣ņä▒ļ░®Ē¢źņŚÉ ņØśĒĢ┤ ĒśĖņÜ░ņé¼ņāüņØ┤ ņØ┤ļÅÖĒĢśļŖö ņŻ╝ļÉ£ Ļ▓ĮļĪ£ņŚÉ Ļ░ĢņÜ░Ļ░Ć ņ¦æņżæļÉśļŖö Ļ▓āņØĆ ļŗ╣ņŚ░ĒĢśļ»ĆļĪ£ Ļ░ĢņÜ░Ļ░ĢļÅä Ļ░Ćņżæņ╣śļź╝ ļ╣äĻĄÉņØś ĻĖ░ņżĆņ£╝ļĪ£ ņäżņĀĢĒĢśņśĆļŗż. ņ”ē, ņĀäņ▓┤ Ļ▓®ņ×ÉņŚÉ Ļ░ĢņÜ░Ļ░ĢļÅäĻ░Ć ņĪ┤ņ×¼ĒĢśļŖö ņ×ģļĀźĻ░ĢņÜ░ņןņØś step 50ņŚÉņä£ņØś Ļ░ĢņÜ░ ņĢÖņāüļĖö ļ®żļ▓äņÖĆ Ļ░ĢņÜ░Ļ░ĢļÅä Ļ░Ćņżæņ╣śņØś ĒśĢĒā£ļź╝ ļ╣äĻĄÉĒĢśņśĆļŗż. ņØ┤ļĢī ĒÅēĻ░ĆņØś ņ▓ÖļÅäļĪ£ļŖö ļæÉ Ļ▓®ņ×ÉĒśĢ Ļ░ĢņÜ░ņןņØś ĒśĢĒā£Ļ░ä ņ£Āņé¼ņä▒ņØä ņĀĢļ¤ēĒÖöĒĢ£ ņāüĻ┤ĆĻ│äņłśļź╝ ņØ┤ņÜ®ĒĢśņśĆļŗż. ļśÉĒĢ£, Ļ░ĢņÜ░Ļ░ĢļÅä Ļ░Ćņżæņ╣śĻ░Ć 0ļČĆĒä░ 1 ņé¼ņØ┤ņØś Ļ░ÆņØ┤ļ»ĆļĪ£ Ļ░ĢņÜ░ ņĢÖņāüļĖö ļ®żļ▓äņØś Ļ▓®ņ×Éļ│ä Ļ░ĢņÜ░Ļ░ĢļÅäļź╝ 0ļČĆĒä░ 1ņé¼ņØ┤ņØś Ļ░Æņ£╝ļĪ£ ņĀĢĻĘ£ĒÖöĒĢ£ Ēøä ļ╣äĻĄÉĒĢśņśĆļŗż. Fig. 10ņØĆ Ļ░ĢņÜ░ ņĢÖņāüļĖö ļ®żļ▓ä 100Ļ░£ņØś Ļ░ĢņÜ░Ļ░ĢļÅä Ļ░Ćņżæņ╣śņÖĆņØś ņāüĻ┤ĆĻ│äņłś ņé░ņĀĢ Ļ▓░Ļ│╝ļź╝ Ē׳ņŖżĒåĀĻĘĖļשņ£╝ļĪ£ ļéśĒāĆļéĖ Ļ▓āņØ┤ļŗż. Case 1ņØś Ļ▓ĮņÜ░ņŚÉļŖö 0.56ņŚÉņä£ 0.64 ņé¼ņØ┤ņØś Ļ░Æņ£╝ļĪ£ ņāüĻ┤ĆĻ│äņłśĻ░Ć ņé░ņĀĢļÉśņŚłĻ│Ā, Case 2ņØĖ Ļ▓ĮņÜ░ņØś ņāüĻ┤ĆĻ│äņłś ņé░ņĀĢ ļ▓öņ£äļŖö 0.67~0.75ņśĆļŗż. ņØ┤ļŖö Ļ░ĢņÜ░ ņĢÖņāüļĖö ļ®żļ▓äņØś ļ▓ĀĒāĆļČäĒż ĻĖ░ļ░ś ņØ┤ļÅÖ ļ¬©ņØśĻ░Ć ņĀüņĀłĒ׳ ņØ┤ļŻ©ņ¢┤ņĪīņØīņØä ņØśļ»ĖĒĢ£ļŗż. Case 2ļ│┤ļŗżļŖö Case 1ņØś ņāüĻ┤ĆĻ│äņłśĻ░Ć ļŗżņåī Ēü¼Ļ▓ī Ļ▓░ņĀĢļÉ£ ņĀÉņØĆ Case 1ņØś Ļ░ĢņÜ░ ņĢÖņāüļĖö ļ®żļ▓äĻ░Ć Ļ░ĢņÜ░ ņØ┤ļÅÖņØś ļ│ĆļÅÖņä▒ņØ┤ ļŹö Ēü¼ĻĖ░ ļĢīļ¼ĖņØĖ Ļ▓āņ£╝ļĪ£ ĒĢ┤ņäØļÉ£ļŗż.
Ļ░ĢņÜ░ ņĢÖņāüļĖö ĒÅēĻĘĀņŚÉ ļīĆĒĢ┤ņä£ļÅä Ļ░ĢņÜ░Ļ░ĢļÅä Ļ░Ćņżæņ╣śņÖĆ ļ╣äĻĄÉĒĢśņśĆļŗż. ņØ┤ļĢīņŚÉļÅä Ļ░ĢņÜ░ ņĢÖņāüļĖö ļ®żļ▓äņŚÉ ļīĆĒĢ£ ĒÅēĻ░Ć ļ░®ļ▓ĢĻ│╝ ļÅÖņØ╝ĒĢśĻ▓ī ņāüĻ┤ĆĻ│äņłśļź╝ ņé░ņĀĢĒĢśņśĆļŗż. ņāüĻ┤ĆĻ│äņłś ņé░ņĀĢ Ļ▓░Ļ│╝, Ļ░ĢņÜ░ ņĢÖņāüļĖö ĒÅēĻĘĀĻ│╝ Ļ░ĢņÜ░Ļ░ĢļÅä Ļ░Ćņżæņ╣śņØś Ļ│ĄĻ░ä ļČäĒżĻ░Ć ļ¦żņÜ░ ņ£Āņé¼ĒĢśĻ▓ī ļéśĒāĆļé¼ļŗż. Case 1ņØś ņāüĻ┤ĆĻ│äņłśļŖö 0.7820, Case 2ņØś ņāüĻ┤ĆĻ│äņłśļŖö 0.7909ļĪ£, ļæÉ Ļ▓ĮņÜ░ ļ¬©ļæÉ ļåÆĻ▓ī ņé░ņĀĢļÉśņŚłļŗż. ņĢ×ņä£ Ļ░ĢņÜ░ ņĢÖņāüļĖö ļ®żļ▓äņŚÉ ļīĆĒĢ┤ ņé░ņĀĢĒĢ£ ņāüĻ┤ĆĻ│äņłśļ│┤ļŗż Ļ░ĢņÜ░ ņĢÖņāüļĖö ĒÅēĻĘĀņØś ņāüĻ┤ĆĻ│äņłśĻ░Ć ļŹö Ēü¼ļŗż. ņØ┤ļŖö Ļ░ĢņÜ░ ņĢÖņāüļĖö ļ®żļ▓äļŖö ļ│ĆļÅÖņä▒ņØ┤ Ēü¼ĻĖ░ ļĢīļ¼ĖņŚÉ ņĀäņ▓┤ņĀüņ£╝ļĪ£ Ļ░ĢņÜ░Ļ░ĢļÅä Ļ░Ćņżæņ╣śņÖĆņØś ĒśĢĒā£ņĀü ņ£Āņé¼ņä▒ņØ┤ ļ¢©ņ¢┤ņ¦Ćņ¦Ćļ¦ī, Ļ░ĢņÜ░ ņĢÖņāüļĖö ļ®żļ▓äņØś ļ│ĆļÅÖņä▒ņØä ļ¬©ļæÉ Ļ│ĀļĀżĒĢśĻ▓ī ļÉśļŖö Ļ░ĢņÜ░ ņĢÖņāüļĖö ĒÅēĻĘĀņØ┤ Ļ░ĢņÜ░Ļ░ĢļÅä Ļ░Ćņżæņ╣śņÖĆ ļŹö ņ£Āņé¼ĒĢ£ ĒŖ╣ņä▒ņØä ļ│┤ņØ┤ļŖö Ļ▓āņ£╝ļĪ£ ĒīÉļŗ©ļÉ£ļŗż.
Ļ░ĢņÜ░Ļ░ĢļÅä Ļ░Ćņżæņ╣śņŚÉ ļīĆĒĢ┤ ĒÅēĻ░ĆĒĢ£ Ļ▓░Ļ│╝, Ļ░ĢņÜ░ ņĢÖņāüļĖö ļ®żļ▓äļ│┤ļŗżļŖö Ļ░ĢņÜ░ ņĢÖņāüļĖö ĒÅēĻĘĀņØ┤ Ļ░ĢņÜ░Ļ░ĢļÅä Ļ░Ćņżæņ╣śņÖĆ ļŹö ņ£Āņé¼ĒĢ£ ĒśĢĒā£ņ×äņØä ĒÖĢņØĖĒĢśņśĆļŗż. Ļ░ĢņÜ░ ņĢÖņāüļĖö ļ®żļ▓äļŖö ļ▓ĀĒāĆļČäĒżļĪ£ļČĆĒä░ ļ░£ņāØļÉ£ ĒŖ╣ņä▒ļ░®Ē¢źņØä ĻĖ░ļ░śņ£╝ļĪ£ ļ¬©ņØśĒĢ£ Ļ▓░Ļ│╝ņØ┤ļŗż. ļö░ļØ╝ņä£ 100Ļ░£ņØś Ļ░ĢņÜ░ ņĢÖņāüļĖö ļ®żļ▓äļŖö Ļ░ü ļ¬©ņØśņŗ£ ļ¼┤ņ×æņ£äņä▒ņØä ĒżĒĢ©ĒĢśļŖö ĒŖ╣ņä▒ļ░®Ē¢źĻ│╝ ņ£Āņé¼ĒĢ£ ĒśĢĒā£ļź╝ Ļ░Ćņ¦ł Ļ░ĆļŖźņä▒ņØ┤ Ēü¼ļŗż. ĻĘĖļ¤¼ļéś Ļ░ĢņÜ░ ņĢÖņāüļĖöņØś ĒÅēĻĘĀņØĆ Ļ░£Ļ░£ Ļ░ĢņÜ░ ņĢÖņāüļĖöņØś ļ│ĆļÅÖņä▒ņØ┤ ņĀ£Ļ▒░ļÉ£ Ļ▓āņØ┤ļ»ĆļĪ£ ĒŖ╣ņä▒ļ░®Ē¢źņØś ĒÅēĻĘĀņĀüņØĖ Ļ▒░ļÅÖņØä ļ│┤ļŗż ņל ļ░śņśüĒĢ£ļŗżĻ│Ā ĒīÉļŗ©ĒĢĀ ņłś ņ׳ļŗż. ļśÉĒĢ£, ņĢ×ņä£ ņ¢ĖĻĖēĒĢ£ Ļ▓āĻ│╝ Ļ░ÖņØ┤, ņ£ĀļÅäļÉ£ Ļ░ĢņÜ░Ļ░ĢļÅä Ļ░Ćņżæņ╣śļŖö ĒŖ╣ņä▒ļ░®Ē¢źņØä ļ░śņśüĒĢ£ Ļ▓āņØ┤ļ»ĆļĪ£ Ļ░ĢņÜ░ ņØ┤ļÅÖ ļ¬©ņØśĻ▓░Ļ│╝ņØĖ ņĢÖņāüļĖö ļ®żļ▓äļŖö Ļ░ĢņÜ░Ļ░ĢļÅä Ļ░Ćņżæņ╣śņÖĆ ņ£Āņé¼ĒĢ£ Ļ│ĄĻ░äļČäĒżĒŖ╣ņä▒ņØä ļ│┤ņØ┤ļŖö Ļ▓āņØ┤ ļŗ╣ņŚ░ĒĢśļŗż.
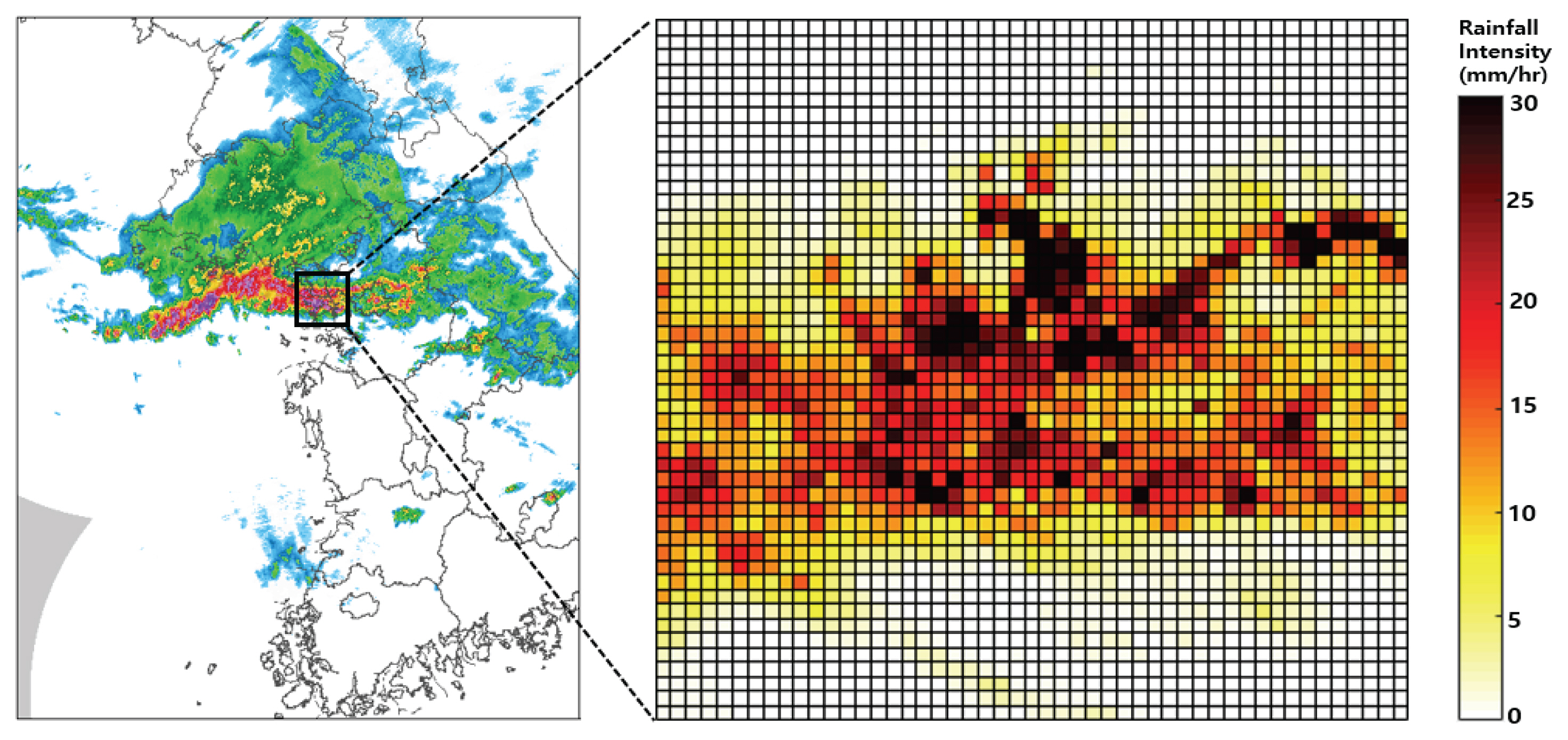
ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö 2018ļģä 8ņøö 28ņØ╝ņŚÉ ļ░£ņāØĒĢ£ ņŗżņĀ£ ĒśĖņÜ░ņé¼ņāüņØä ļīĆņāüņ£╝ļĪ£ ņĢÖņāüļĖö ļ®żļ▓äļź╝ ļ¬©ņØśĒĢśĻ│Ā ĒÅēĻ░ĆĒĢśņśĆļŗż. ņ”ē, ņĢÖņāüļĖö ļ®żļ▓ä ņāØņä▒ņŚÉ ĒĢäņÜöĒĢ£ ņ×ģļĀźĻ░ĢņÜ░ņןņØä ņŗżņĀ£ ĒśĖņÜ░ņØś ļĀłņØ┤ļŹö Ļ┤ĆņĖĪ Ļ░ĢņÜ░ņןņ£╝ļĪ£ ņäżņĀĢĒĢśņśĆļŗż. ņØ┤ ĒśĖņÜ░ņé¼ņāüņØĆ ņØ┤ļÅÖņåŹļÅäĻ░Ć ļ╣äĻĄÉņĀü ļ╣ĀļźĖ ĻĄŁņ¦Ćņä▒ ņ¦æņżæĒśĖņÜ░ņŚÉ ĒĢ┤ļŗ╣ĒĢśļ®░, ņä£ņÜĖĻĖ░ņāüļīĆņŚÉņä£ Ļ┤ĆņĖĪļÉ£ ņØ╝Ļ░ĢņÜ░ļ¤ēņØĆ 96.5 mmņØ┤ļŗż. ļśÉĒĢ£, ņØ┤ ĒśĖņÜ░ņé¼ņāüņØĆ ņä£ņ¬ĮņŚÉņä£ ļÅÖņ¬Įņ£╝ļĪ£ ņØ┤ļÅÖĒĢśļŖö ĒŖ╣ņä▒ņØä ļ│┤ņØĖļŗż. ĒśĖņÜ░ ĻĖ░Ļ░ä ņżæ 17ņŗ£ 50ļČäņŚÉ Ļ┤ĆņĖĪļÉ£ ļĀłņØ┤ļŹö Ļ┤ĆņĖĪņןņØĆ Fig. 11Ļ│╝ Ļ░ÖņØĆļŹ░, Ļ░ĢĒĢ£ Ļ░ĢņÜ░Ļ░Ć ņä£ņÜĖĒŖ╣ļ│äņŗ£ļĪ£ ņ£Āņ×ģļÉśļŖö ĒśĢĒā£ļź╝ ļ│┤ņØ┤ĻĖ░ ļĢīļ¼ĖņŚÉ Ļ░ĢņÜ░ņØś ņØ┤ļÅÖ ļ¬©ņØśņŚÉ ņĀüĒĢ®ĒĢ£ Ļ▓ĮņÜ░ļĪ£ ļ│╝ ņłś ņ׳ļŗż. ļö░ļØ╝ņä£ ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö 17ņŗ£ 50ļČäņŚÉ Ļ┤ĆņĢģņé░ ĻĖ░ņāüļĀłņØ┤ļŹöņŚÉņä£ Ļ┤ĆņĖĪļÉ£ 1.5 km CAPPI ņ×ÉļŻīļĪ£ļČĆĒä░ ļĀłņØ┤ļŹö Ļ░ĢņÜ░Ļ░ĢļÅäļź╝ ņé░ņČ£ĒĢśņŚ¼ ņĢÖņāüļĖö ļ®żļ▓ä ņāØņä▒ ļ¬©ņØśņŚÉ ņØ┤ņÜ®ĒĢśņśĆļŗż. ņØ┤ļĢī ļĀłņØ┤ļŹö Ļ░ĢņÜ░Ļ░ĢļÅä ņé░ņČ£ņŚÉļŖö Marshall and Palmer (1948)Ļ░Ć ņĀ£ņŗ£ĒĢ£ Z = 200R1.6 Ļ┤ĆĻ│äņŗØņØä ņØ┤ņÜ®ĒĢśņśĆļŗż. ņ×ģļĀźĻ░ĢņÜ░ņןņØĆ ņØ┤ļÅÖ ļ¬©ņØśĻ░Ć Ļ░ĆļŖźĒĢśļÅäļĪØ 1 km2 Ēü¼ĻĖ░ņØś Ļ▓®ņ×É 50 ├Ś 50Ļ░£ļĪ£ Ļ│ĄĻ░äĒĢ┤ņāüļÅäļź╝ ņĪ░ņĀĢĒĢśņśĆļŗż.
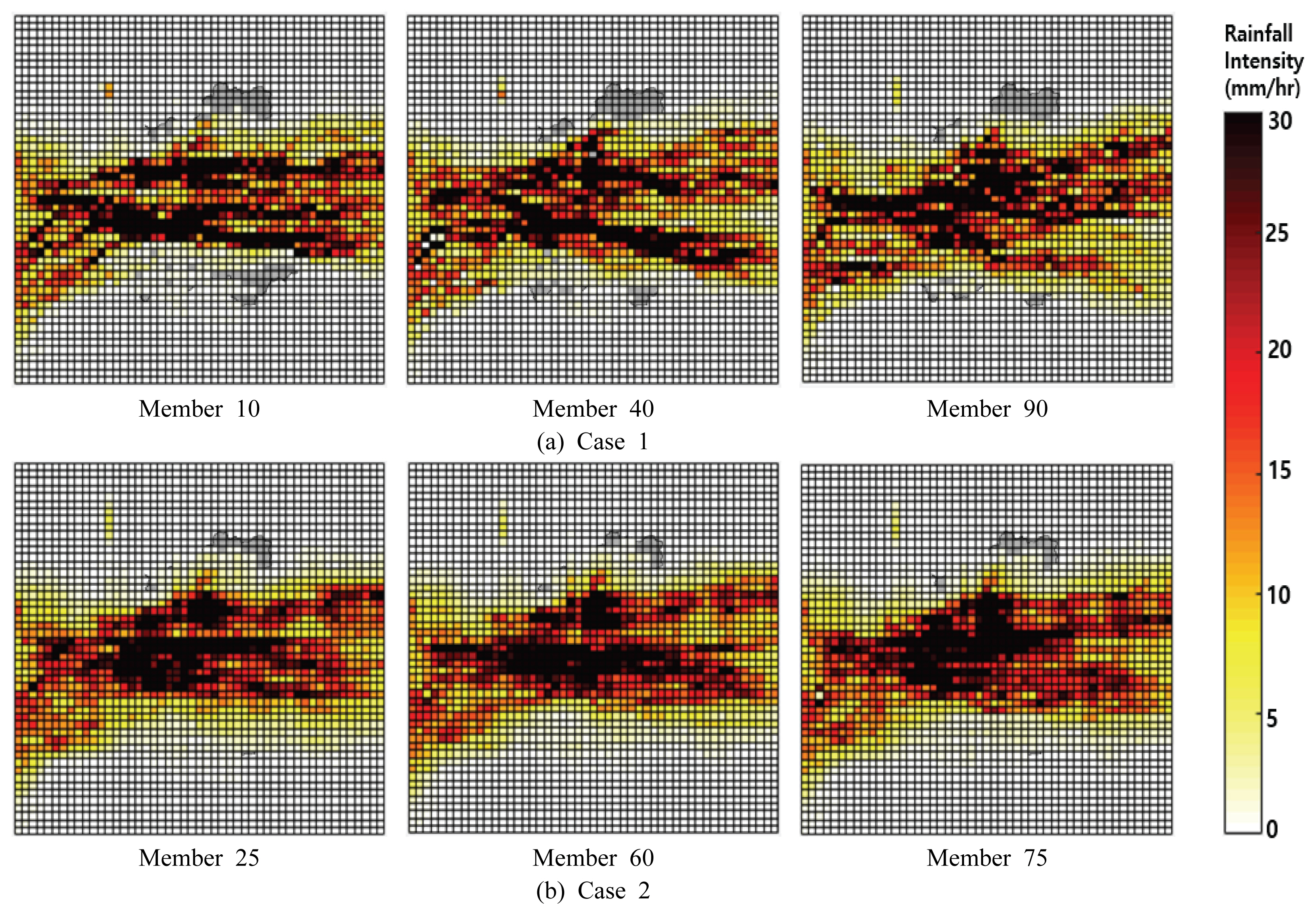
Ļ┤ĆņĖĪ Ļ░ĢņÜ░ņןņŚÉ ļīĆĒĢ┤ 100ĒÜī ņØ┤ļÅÖļ¬©ņØśĒĢśņŚ¼ ņ┤Ø 100Ļ░£ņØś Ļ░ĢņÜ░ ņĢÖņāüļĖö ļ®żļ▓äļź╝ ņāØņä▒ĒĢśņśĆļŗż. ĻĘĖļ”╝ Fig. 12(a)ļŖö Case 1ņŚÉ ļīĆĒĢ┤ ņāØņä▒ĒĢ£ Ļ░ĢņÜ░ ņĢÖņāüļĖö ļ®żļ▓ä ņżæ 10, 40, 90ļ▓łņ¦Ė ļ®żļ▓äļōżņØś step 50ņŚÉņä£ņØś ļ¬©ņØś ņāüĒā£ļź╝ ļéśĒāĆļéĖ Ļ▓āņØ┤ļ®░, Fig. 12(b)ļŖö Case 2ņØś 25, 60, 75ļ▓łņ¦Ė ļ®żļ▓äņØ┤ļŗż. Case 1Ļ│╝ Case 2ņØś ņĢÖņāüļĖö ļ®żļ▓äļŖö ņĀäņ▓┤ņĀüņØĖ Ļ░ĢņÜ░Ļ░ĢļÅäņØś Ļ│ĄĻ░äņĀü ļČäĒż Ļ▓ĮĒ¢źņØĆ ņ£Āņé¼ĒĢ£ Ļ▓āņ£╝ļĪ£ ļéśĒāĆļé¼ļŗż. ņ”ē, Case 1Ļ│╝ Case 2 ļ¬©ļæÉ ņ×ģļĀźļÉ£ Ļ░ĢņÜ░ņןņØ┤ ĒŖ╣ņä▒ļ░®Ē¢źņØś ņĀäņ▓┤ņĀüņØĖ Ļ▓ĮĒ¢źņŚÉ ļö░ļØ╝ ņżæņĢÖļČĆļĪ£ ņ¦æņżæļÉśļŖö ĒśĢĒā£ļź╝ ļ│┤ņśĆļŗż. ĻĘĖļ¤¼ļéś Case 1ņØś Ļ▓ĮņÜ░, Case 2ņŚÉ ļ╣äĒĢ┤ ĒŖ╣ņĀĢ Ļ▓ĮļĪ£ņŚÉ Ļ░ĢņÜ░ ņØ┤ļÅÖņØ┤ ņ¦æņżæļÉśļŖö ĒśäņāüņØ┤ ļŹö ļÜ£ļĀĘĒĢśĻ▓ī ļéśĒāĆļé¼ņ£╝ļ®░, 100Ļ░£ ļ®żļ▓äļōżņØś ļ¬©ņØś Ļ▓░Ļ│╝Ļ░Ć ļŹö ņāüņØ┤ĒĢ£ ĒśĢĒā£ņ×äņØä ĒÖĢņØĖĒĢśņśĆļŗż. ņØ┤ļ¤¼ĒĢ£ ņ░©ņØ┤ļŖö ļé£ņłśļ░£ņāØ ļ▓öņ£äļź╝ ņ¢┤ļ¢╗Ļ▓ī ņäżņĀĢĒĢśļŖÉļāÉņŚÉ ņśüĒ¢źņØä ļ░øļŖöļŗż. Ļ▓®ņ×Éļ│ä ĒŖ╣ņä▒ļ░®Ē¢ź Ļ░Ćņżæņ╣śņØś ņĄ£ļīĆĻ░ÆĻ│╝ ņĄ£ņåīĻ░ÆņØś ņ░©ņØ┤ņŚÉ ĒĢ┤ļŗ╣ĒĢśļŖö ĻĄ¼Ļ░äņ£╝ļĪ£ ņäżņĀĢĒĢ£ Case 1ņØ┤ 90%ļź╝ ĒżĒĢ©ĒĢśļŖö ĻĄ¼Ļ░äņ£╝ļĪ£ ņäżņĀĢĒĢ£ Case 2ņŚÉ ļ╣äĒĢ┤ Ļ░ĢņÜ░Ļ░ĢļÅäņØś ļ¼┤ņ×æņ£äņä▒ņØ┤ ļŹö Ēü¼Ļ▓ī ļéśĒāĆļéśļŖö Ļ▓āņØĆ ļŗ╣ņŚ░ĒĢśļŗż.
Ļ┤ĆņĖĪ Ļ░ĢņÜ░ņןņŚÉ ļīĆĒĢ£ ņĢÖņāüļĖö ļ®żļ▓ä ņāØņä▒ ļ░Å ĒÅēĻ░Ć Ļ▓░Ļ│╝, Ļ░ĢņÜ░ ņĢÖņāüļĖö ļ®żļ▓ä ņāØņä▒ņŗ£ ņ¦ĆņŚŁĒŖ╣ņä▒ņØ┤ ļ░śņśüļÉśļ®░, ļ¬©ņØś Ļ▓░Ļ│╝ļŖö ļ▓ĀĒāĆļČäĒżņØś ļé£ņłśļ░£ņāØ ļ▓öņ£ä ņ”ē, Ēæ£ņżĆĒÄĖņ░©ņŚÉ ļ»╝Ļ░ÉĒĢ£ ņśüĒ¢źņØä ļ░øļŖöļŗżļŖö ņĀÉņØä ĒÖĢņØĖĒĢśņśĆļŗż. ļ©╝ņĀĆ, ņĀäņ▓┤ņĀüņØĖ Ļ░ĢņÜ░ ņØ┤ļÅÖ ļ¬©ņØśņØś Ļ▓ĮĒ¢źņä▒ņØĆ ņ¦ĆņŚŁĒŖ╣ņä▒ Ļ░Ćņżæņ╣śņØĖ ĒŖ╣ņä▒ļ░®Ē¢źĻ│╝ ņ£Āņé¼ĒĢśņśĆļŗż. ņ”ē, Fig. 12ņŚÉņä£ņÖĆ Ļ░ÖņØ┤ step 50ņŚÉņä£ ĒśĖņÜ░Ļ░Ć ņżæņĢÖļČĆļĪ£ ņ¦æņżæļÉśļŖö ĒśäņāüņØ┤ Ļ│ĄĒåĄņĀüņ£╝ļĪ£ ļéśĒāĆļé¼ļŗż. ļśÉĒĢ£, ļ▓ĀĒāĆļČäĒżņØś ļé£ņłśļ░£ņāØ ļ▓öņ£äļź╝ ņ¢┤ļ¢╗Ļ▓ī ņäżņĀĢĒĢśļŖÉļāÉņŚÉ ļö░ļØ╝ ņĢÖņāüļĖö ļ®żļ▓äĻ░äņØś ņ░©ņØ┤Ļ░Ć ļŗ¼ļØ╝ņ¦äļŗżļŖö ņĀÉņØä ĒÖĢņØĖĒĢśņśĆļŗż. Fig. 12ņŚÉņä£ ļ│╝ ņłś ņ׳ļō»ņØ┤ Case 1ļ│┤ļŗż Case 2ņØś ņĢÖņāüļĖö ļ®żļ▓äļŖö ņä£ļĪ£ ņ░©ņØ┤Ļ░Ć ņĀüļŗż. ņØ┤ļŖö Case 2ņØś ļ▓ĀĒāĆļČäĒż ĻĖ░ļ░ś ļé£ņłśļ░£ņāØņØś ļ▓öņ£äĻ░Ć ļŹö ņ×æĻĖ░ ļĢīļ¼ĖņØ┤ļŗż. ļé£ņłśļ░£ņāØņØś ļ▓öņ£äļŖö ņĀüņÜ® ļīĆņāü ņ¦ĆņŚŁ ļ░Å Ļ│╝Ļ▒░ ĒśĖņÜ░ņé¼ņāüņØś ĒŖ╣ņä▒ņŚÉ ļö░ļØ╝ ļŗżņ¢æĒĢśĻ▓ī ņĀüņÜ®ĒĢĀ ņłś ņ׳ļŗż. ņ”ē, ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ ņĀ£ņĢłĒĢśļŖö ĻĖ░ļ▓ĢņØś ņé¼ņÜ®ņ×ÉĻ░Ć ņ×äņØśļĪ£ ņäżņĀĢĒĢśļ®┤ ļÉ£ļŗż. ņČöĒøä ņŚ░ĻĄ¼ļź╝ ĒåĄĒĢ┤ ĒśĖņÜ░ ĒŖ╣ņä▒ ļ░Å ņŚ¼ļ¤¼ ņāüĒÖ®ņŚÉ ņĀüĒĢ®ĒĢ£ ļ▓ĀĒāĆļČäĒżņØś Ēæ£ņżĆĒÄĖņ░© ļ▓öņ£äļź╝ ņĀ£ņŗ£ĒĢĀ ņłśļÅä ņ׳ņØä Ļ▓āņØ┤ļŗż.
ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö ņ¦ĆņŚŁņĀüņØĖ ĒŖ╣ņä▒ņØä Ļ│ĀļĀżĒĢśņŚ¼ Ļ░ĢņÜ░ ņĢÖņāüļĖö ļ®żļ▓äļź╝ ņāØņä▒ĒĢśļŖö ĻĖ░ļ▓ĢņØä ņĀ£ņĢłĒĢśņśĆļŗż. ļśÉĒĢ£, ņāØņä▒ļÉ£ Ļ░ĢņÜ░ ņĢÖņāüļĖö ļ®żļ▓äņŚÉ ļīĆĒĢ£ ĒÅēĻ░Ćļź╝ ņłśĒ¢ēĒĢśņśĆļŗż. ņ¦ĆņŚŁĒŖ╣ņä▒ņ£╝ļĪ£ļŖö Ļ▓®ņ×Éļ│ä Ļ░ĢņÜ░ņØś ņØ┤ļÅÖļ░®Ē¢źĻ│╝ Ļ░ĢņÜ░Ļ░ĢļÅäļź╝ Ļ│ĀļĀżĒĢśņśĆļŗż. ļīĆņāü ņ¦ĆņŚŁņŚÉ ļīĆĒĢ┤ ļ¬©ņØś Ļ▓®ņ×Éļ¦ØņØä ĻĄ¼ņČĢĒĢśĻ│Ā Ļ▓®ņ×Éļ│äļĪ£ ĒŖ╣ņä▒ļ░®Ē¢źĻ│╝ Ļ░ĢņÜ░Ļ░ĢļÅä Ļ░Ćņżæņ╣śļź╝ Ļ▓░ņĀĢĒĢśņśĆļŗż. Ļ▓░ņĀĢļÉ£ Ļ▓®ņ×Éļ│ä Ļ░Ćņżæņ╣śņØś ĒåĄĻ│äĒĢÖņĀü ĒŖ╣ņä▒ņ╣śļź╝ ņØ┤ņÜ®ĒĢśņŚ¼ ļ▓ĀĒāĆļČäĒżļź╝ ņ£ĀļÅäĒĢśĻ│Ā, ņØ┤ļĪ£ļČĆĒä░ ņāØņä▒ļÉ£ ļé£ņłśļź╝ ĻĖ░ļ░śņ£╝ļĪ£ ņ×ģļĀźĻ░ĢņÜ░ņןņØś ņØ┤ļÅÖ ļ¬©ņØśļź╝ ņłśĒ¢ēĒĢśņśĆļŗż. ņ×ģļĀźĻ░ĢņÜ░ņןņØś ĒśĢĒā£ļŖö Ļ▓®ņ×Éļ¦Ø ņĀäņ▓┤ņŚÉ Ļ░ĢņÜ░Ļ░ĢļÅäĻ░Ć ņĪ┤ņ×¼ĒĢśļŖö Ļ▓ĮņÜ░, ņäĖļĪ£ ļ¦ēļīĆĒśĢ, Ļ░ĆļĪ£ ļ¦ēļīĆĒśĢ, ņøÉĒśĢņØä Ļ│ĀļĀżĒĢśņśĆļŗż. ņ×ģļĀźĻ░ĢņÜ░ņןņŚÉ ļīĆĒĢ┤ ņ┤Ø 100ĒÜī ļ¬©ņØśļź╝ ņłśĒ¢ēĒĢśņŚ¼ Ļ░ĢņÜ░ ņØ┤ļÅÖ ļ¬©ņØś Ļ▓░Ļ│╝ņŚÉ ĒĢ┤ļŗ╣ĒĢśļŖö ņĢÖņāüļĖö ļ®żļ▓äļź╝ 100Ļ░£ ņāØņä▒ĒĢśņśĆļŗż. ņĄ£ņóģņĀüņ£╝ļĪ£ ņāØņä▒ļÉ£ Ļ░ĢņÜ░ ņĢÖņāüļĖö ļ®żļ▓äņÖĆ Ļ░ĢņÜ░ ņĢÖņāüļĖö ĒÅēĻĘĀņØĆ Ļ░ĢņÜ░Ļ░ĢļÅä Ļ░Ćņżæņ╣śļź╝ ĻĖ░ņżĆņ£╝ļĪ£ ļ╣äĻĄÉ ļ░Å ĒÅēĻ░ĆĒĢśņśĆļŗż. ņČöĻ░ĆņĀüņ£╝ļĪ£ 2018ļģä 8ņøöņŚÉ ņä£ņÜĖņ¦ĆņŚŁņŚÉņä£ ļ░£ņāØĒĢ£ ņŗżņĀ£ ĒśĖņÜ░ņé¼ņāüņŚÉ ļīĆĒĢ┤ņä£ļÅä ņĢÖņāüļĖö ļ®żļ▓äļź╝ ņāØņä▒ĒĢśĻ│Ā ĒÅēĻ░ĆĒĢśņśĆļŗż.
ņāØņä▒ļÉ£ Ļ░ĢņÜ░ ņĢÖņāüļĖö ļ®żļ▓äļŖö Ļ░ĢņÜ░Ļ░ĢļÅä Ļ░Ćņżæņ╣śņØś ĒŖ╣ņä▒ņØä ļéśĒāĆļé┤ļŖö Ļ▓āņ£╝ļĪ£ ĒÖĢņØĖļÉśņŚłļŗż. ņøÉĒśĢ ņ×ģļĀźĻ░ĢņÜ░ņןņŚÉ ļīĆĒĢ£ ļ¬©ņØś Ļ▓░Ļ│╝, step 50Ļ╣īņ¦ĆļŖö Ļ░ĢņÜ░Ļ░Ć ņżæņĢÖļČĆļĪ£ ņ¦æņżæļÉśļŖö ĒśĢĒā£ļĪ£ ņØ┤ļÅÖĒĢśļŗżĻ░Ć step 50 ņØ┤ĒøäļĪ£ļŖö ņ¦æņżæļÉ£ ĒśĢĒā£ņØś Ļ░ĢņÜ░Ļ░Ć ņ£Āņ¦ĆļÉśļ®┤ņä£ ņČ£ļĀźļÉśņŚłļŗż. ņØ┤ļ¤¼ĒĢ£ Ļ▓ĮĒ¢źņØĆ ņ×ģļĀźĻ░ĢņÜ░ņןņØś ĒśĢĒā£ņŚÉ Ļ┤ĆĻ│äņŚåņØ┤ Ļ│ĄĒåĄņĀüņ£╝ļĪ£ ļéśĒāĆļé¼ļŗż. ļé£ņłśļ░£ņāØņØś ļ▓öņ£äņŚÉ ļö░ļØ╝ Ļ░ĢņÜ░ ņØ┤ļÅÖ ļ¬©ņØś Ļ▓░Ļ│╝Ļ░Ć Ēü¼Ļ▓ī ļŗżļź┤Ļ▓ī ļéśĒāĆļéśļŖö Ļ▓āņ£╝ļĪ£ ĒÖĢņØĖļÉśņŚłļŗż. ļé£ņłśļ░£ņāØ ļ▓öņ£äļź╝ ĒŖ╣ņä▒ļ░®Ē¢ź Ļ░Ćņżæņ╣śņØś ņĄ£ļīĆĻ░ÆĻ│╝ ņĄ£ņåīĻ░Æ ņ░©ņØ┤ļĪ£ ņäżņĀĢĒĢ£ Case 1ņØ┤ ņØ┤ļ│┤ļŗż ņóĆ ļŹö ņ×æņØĆ, 90% ņ×ÉļŻīļź╝ ĒżĒĢ©ĒĢśļŖö ĻĄ¼Ļ░äņ£╝ļĪ£ ņäżņĀĢĒĢ£ Case 2ņŚÉ ļ╣äĒĢ┤ ņĢÖņāüļĖö ļ®żļ▓äņØś ņ░©ņØ┤Ļ░Ć ļŹöņÜ▒ ļÜ£ļĀĘĒĢśĻ▓ī ļéśĒāĆļé¼ļŗż. ļŗ╣ņŚ░Ē׳ ņĢÖņāüļĖö ļ®żļ▓äņØś ļ¼┤ņ×æņ£äņä▒ļÅä Case 1ņØ┤ ļŹö Ēü¼Ļ▓ī ļéśĒāĆļé¼ņ£╝ļ®░, ņØ┤ļŖö ņāØņä▒ļÉ£ Ļ░ĢņÜ░ ņĢÖņāüļĖö ļ®żļ▓äņÖĆ Ļ░ĢņÜ░Ļ░ĢļÅä Ļ░Ćņżæņ╣śņÖĆņØś ņāüĻ┤ĆĻ│äņłś ļ╣äĻĄÉņŚÉņä£ļÅä ĒÖĢņØĖļÉśņŚłļŗż.
Ļ░ĢņÜ░ ņĢÖņāüļĖö ĒÅēĻĘĀņØĆ Ļ░£Ļ░£ Ļ░ĢņÜ░ ņĢÖņāüļĖö ļ®żļ▓äļōżļ│┤ļŗż Ļ░ĢņÜ░Ļ░ĢļÅä Ļ░Ćņżæņ╣śņÖĆ ļŹö ņ£Āņé¼ĒĢ£ ĒŖ╣ņä▒ņØä ļ│┤ņØ┤ļŖö Ļ▓āņ£╝ļĪ£ ļéśĒāĆļé¼ļŗż. ņ”ē, Ļ░£Ļ░£ Ļ░ĢņÜ░ ņĢÖņāüļĖö ļ®żļ▓äļŖö ņāüļīĆņĀüņ£╝ļĪ£ ļÅģļ”ĮņĀüņØĖ Ļ░ĢņÜ░ņØś ņØ┤ļÅÖ Ļ▓ĮļĪ£ļź╝ ļ│┤ņØ┤ņ¦Ćļ¦ī, ņØ┤ļōżņØś ĒÅēĻĘĀņØĆ ņØ┤ļÅÖ Ļ▓ĮļĪ£ņØś ĒÅēĒÖ£ĒÖöļź╝ Ļ░ĆņĀĖņÖĆ Ļ▓░ĻĄŁ Ļ░ĢņÜ░Ļ░ĢļÅä Ļ░Ćņżæņ╣śņØś ĒŖ╣ņä▒ņŚÉ ļŹöņÜ▒ ĻĘ╝ņĀæĒĢśļŖö Ļ▓āņ£╝ļĪ£ ĒÖĢņØĖļÉśņŚłļŗż. ņØ┤ļ¤¼ĒĢ£ Ļ▓░Ļ│╝ļŖö ņĢÖņāüļĖö ņśłņĖĪņØś ļ¬®ņĀüņŚÉ ņל ļČĆĒĢ®ĒĢśļŖö Ļ▓░Ļ│╝ļĪ£ ņØ┤ĒĢ┤ļÉ£ļŗż. ņ”ē, Ļ░£Ļ░£ ņĢÖņāüļĖö ļ®żļ▓äļŖö ņŗżĒśä Ļ░ĆļŖźĒĢ£ Ļ▓ĮņÜ░ļōżņØä Ļ░£ļ│äņĀüņ£╝ļĪ£ ļ░śņśüĒĢśņ¦Ćļ¦ī, ĻĘĖļōżņØś ĒÅēĻĘĀņØĆ Ļ▓░ĻĄŁ ņŻ╝ņ¢┤ņ¦ä ņČöņäĖļź╝ ļ░śņśüĒĢśļŖö ĒśĢĒā£ļĪ£ ņłśļĀ┤ļÉśļŖö Ļ▓āņØ┤ļŗż.
ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ ņĀ£ņŗ£ĒĢ£ ņ¦ĆņŚŁĒŖ╣ņä▒ņØä Ļ│ĀļĀżĒĢ£ Ļ░ĢņÜ░ ņĢÖņāüļĖö ļ®żļ▓ä ņāØņä▒ ĻĖ░ļ▓ĢņØĆ ņČöĒøä ĒÖĢņן ņĀüņÜ®ņØ┤ Ļ░ĆļŖźĒĢśļŗż. ļ©╝ņĀĆ, ņŗżņĀ£ ĒśĖņÜ░ņé¼ņāüņŚÉ ļīĆĒĢ£ ļĀłņØ┤ļŹö Ļ┤ĆņĖĪņ×ÉļŻī Ēś╣ņØĆ ņśłņĖĪņ×ÉļŻīņŚÉ ļ│Ė ĻĖ░ļ▓ĢņØä ņŗżņŗ£Ļ░äņ£╝ļĪ£ ņĀüņÜ®ĒĢśņŚ¼ ļÅäņŗ£ĒÖŹņłśņśłĻ▓Įļ│┤ņŚÉ ņØ┤ņÜ®ļÉĀ ņłś ņ׳ļŗż. ļ¼╝ļĪĀ ņØ┤ Ļ▓ĮņÜ░ņŚÉļŖö ņśłņĖĪņ×ÉļŻīņØś ĒÆłņ¦ł Ē¢źņāü ļ░Å ņäĀĒ¢ēņŗ£Ļ░ä ĒÖĢļ│┤ ļō▒ņØ┤ Ļ│ĀļĀżļÉśņ¢┤ņĢ╝ ĒĢĀ Ļ▓āņØ┤ļŗż. ĻĖ░ņłĀņĀüņØĖ ņĖĪļ®┤ņŚÉņä£ ņĢÖņāüļĖö ļ®żļ▓äņØś ļŗżņ¢æĒÖö ņĀĢļÅäļŖö ļ▓ĀĒāĆļČäĒżņØś ļé£ņłśļ░£ņāØ ļ▓öņ£äļź╝ ņ¢┤ļ¢╗Ļ▓ī Ļ▓░ņĀĢĒĢśļŖÉļāÉņØś ļ¼ĖņĀ£ņØ┤ļŗż. ņØ┤ļź╝ ņ£äĒĢ┤ņä£ļŖö ļīĆņāü ņ¦ĆņŚŁņŚÉ ļīĆĒĢ£ ļ│┤ļŗż ņŗ¼ļÅäņ׳ļŖö ņ×ÉļŻīļČäņäØ ļ░Å ļ╣äĻĄÉĒÅēĻ░ĆĻ░Ć ĒĢäņÜöĒĢśļŗż. ļ│┤ļŗż ļŗżņ¢æĒĢ£ ĒśĢĒā£ņØś ĒśĖņÜ░ņŚÉ ļīĆĒĢ£ ļ¬©ņØśļÅä ĒĢäņÜöĒĢśļŗż. ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö ņĀüņÜ® ņé¼ļĪĆļĪ£ ņä£ņ¬ĮņŚÉņä£ ļÅÖņ¬Įņ£╝ļĪ£ ņØ┤ļÅÖĒĢśļŖö ĒśĖņÜ░ļź╝ ļŗżļŻ©Ļ│Ā ņ׳ņ£╝ļéś, Ēā£ĒÆŹ ļō▒ņØś Ļ▓ĮņÜ░ņŚÉļŖö ļé©ļČü ļśÉļŖö ļé©ņä£ņŚÉņä£ ļČüļÅÖņØś ņé¼ņäĀ ļ░®Ē¢źņ£╝ļĪ£ ņØ┤ļÅÖĒĢśļ»ĆļĪ£ ņØ┤ņŚÉ ļīĆĒĢ£ ņĀüņÜ®ņä▒ Ļ▓ĆĒåĀļÅä ĒĢäņÜöĒĢśļŗż. ļ¼╝ļĪĀ ņØ┤ļ¤¼ĒĢ£ ĒÖĢņןņØä ņ£äĒĢ┤ņä£ļŖö ļ│┤ļŗż ļ¦ÄņØĆ ņŗżņĀ£ ĒśĖņÜ░ņé¼ņāüņŚÉ ļīĆĒĢ£ ļČäņäØņØ┤ ņäĀĒ¢ēļÉśņ¢┤ņĢ╝ ĒĢ£ļŗżļŖö Ļ▓āņØĆ ņ×Éļ¬ģĒĢśļŗż. Ē¢źĒøä ņØ┤ļ¤¼ĒĢ£ ļ¼ĖņĀ£ļōżņŚÉ ļīĆĒĢ£ ņ¦ĆņåŹņĀüņØĖ ņŚ░ĻĄ¼ļź╝ ĒåĄĒĢ┤ Ļ░ĢņÜ░ņśłņĖĪņØś ļ│ĆļÅÖņä▒ ļ░Å ļČłĒÖĢņŗżņä▒ņØä Ļ│ĀļĀżĒĢ£ ņŗżņŗ£Ļ░ä ņĢÖņāüļĖö Ļ░ĢņÜ░ņśłņĖĪņØ┤ Ļ░ĆļŖźĒĢĀ Ļ▓āņØ┤ļŗż.
Ļ░Éņé¼ņØś ĻĖĆ
ļ│Ė ņŚ░ĻĄ¼ļŖö ĒÖśĻ▓ĮļČĆņØś ĒĢ£ĻĄŁĒÖśĻ▓Įņé░ņŚģĻĖ░ņłĀņøÉņØś ļ¼╝Ļ┤Ćļ”¼ņŚ░ĻĄ¼ņé¼ņŚģņØś ņ¦ĆņøÉņØä ļ░øņĢä ņŚ░ĻĄ¼ļÉśņŚłņŖĄļŗłļŗż. (79615)
Table┬Ā1
Transposed Rainfall Intensity for the Grid (i, j) at Fig. 1
Table┬Ā2
Characteristics of the Major Storm Events Occurred at Seoul from 2009 to 2018
References
Baker, LH, Rudd, AC, Migliorini, S, and Bannister, RN (2014) Representation of model error in a convective-scale ensemble prediction system. Nonlin Processes Geophys, Vol. 21, pp. 19-39.


Beran, MA, and Sutcliffe, JV (1972) An index of flood-producing rainfall based on rainfall and soil moisture deficit. J Hydrol, Vol. 17, pp. 229-236.

Bhunya, PK, Berndtsson, R, Ojha, CSP, and Mishra, SK (2007) Suitability of Gamma, Chi-square, Weibull, and beta distributions as synthetic unit hydrographs. J Hydrol, Vol. 334, pp. 28-38.

Bhunya, PK, Mishra, SK, Ojha, CSP, and Berndtsson, R (2004). Parameter estimation of beta distribution for unit hydrograph derivation. J Hydrol Eng. ASCE, Vol. 9: No. 4, p 325-332.

Bowler, NE, Arribas, A, Mylne, KR, Robertson, KB, and Beare, SE (2008) The MOGREPS short-range ensemble prediction system. Q J Royal Meteorol Soc, Vol. 134, pp. 703-722.

Brubaker, KL, and Menoes, M (2001). A technique to estimate snow depletion curves from time-series data using the beta distribution. Proceedings of the 58th Eastern Snow Conference. Ottawa, Ontario, Canada: Vol. 58: pp. 343-346.

Buizza, R (1997) Potential forecast skill of ensemble prediction and spread and skill distributions of the ECMWF ensemble prediction system. Mon Weather Rev, Vol. 125, No. 1, pp. 99-119.

Choi, H, and Nam, KW (2005) Real-time flash flood evaluation by GIS module at mountainous area. Korean Journal of Remote Sensing, Vol. 21, No. 4, pp. 317-327.

Collier, CG (2009) On the propagation of uncertainty in weather radar estimates of rainfall through hydrological models. Meteorol Appl, Vol. 16, No. 1, pp. 35-40.

Cooke, RA, Mostaghimi, S, and Woeste, F (1995) Effect of hydraulic conductivity probability distribution function on simulated solute leaching. Water Environ Res, Vol. 67, No. 2, pp. 159-168.

Dance, S, Ebert, E, and Scurrah, D (2010) Thunderstorm strike probability nowcasting. J Atmos Ocean Technol, Vol. 27, No. 1, pp. 79-93.

Dixon, M, and Wiener, G (1993) TITAN: Thunderstorm identification, tracking, analysis, and nowcasting: A radar-based methodology. J Atmos Ocean Technol, Vol. 10, No. 6, pp. 785-797.

Duan, Q, Ajami, NK, Gao, X, and Sorooshian, S (2007) Multi-model ensemble hydrologic prediction using Bayesian model averaging. Adv Water Resour, Vol. 30, pp. 1371-1386.

Georgakakos, KP, Graham, R, Jubach, R, Carpenter, T, Shamir, E, Spencer, C, et al (2013). Global flash flood guidance system, phase I. Hydrologic Research Center (HRC) Technical Report No. 9. Hydrologic Research Center, San Diego, CA, USA.

Germann, U, and Zawadzki, I (2002) Scale-dependence of the predictability of precipitation from continental radar images. Part I: Description of the methodology. Mon Weather Rev, Vol. 130, pp. 2859-2873.

Hafley, WL, and Schreuder, HT (1977) Statistical distributions for fitting diameter and height data in even-aged stands. Can J For Res, Vol. 7, No. 3, pp. 481-487.

Han, M (2014). Correction from MAPLE and KLAPS rainfall forecasting. Ph.D. dissertation. Korea University; Seoul, Korea.

Hewitt, CD (2004) Ensembles-based predictions of climate changes and their impacts. Eos, Trans Am Geophys Union, Vol. 85, No. 52, pp. 566-566.

Hwang, S, Lim, S, Kim, K, and Yoon, J (2013) Verification of characteristics of radar rainfall observation for a real time application of radar rainfall data. Magazine of Korean Soc Hazard Mitig, Vol. 13, No. 4, pp. 72-79.

Jun, C, and Yoo, C (2012) Application of the beta distribution for the temporal quantification of storm events. J Korea Water Resour Assoc, Vol. 45, No. 6, pp. 531-544.


Jun, C, and Yoo, C (2013) Analysis on the characteristics about representative temporal-distribution of rainfall in the annual maximum independent rainfall events at Seoul using beta distribution. J Korea Water Resour Assoc, Vol. 46, No. 4, pp. 361-372.


Kang, N, Joo, H, Lee, M, and Kim, HS (2017) Generation of radar rainfall ensemble using probabilistic approach. J Korea Water Resour Assoc, Vol. 50, No. 3, pp. 155-167.

Kay, JK, Kim, HM, Park, YY, and Son, J (2013) Effect of doubling the ensemble size on the performance of ensemble prediction in the warm season using MOGREPS implemented at the KMA. Adv Atmos Sci, Vol. 30, pp. 1287-1302.


Kim, B, Hong, J, Kim, HS, and Yoon, S (2007) Development of flash flood model using digital terrain analysis model and rainfall RADAR: I. Methodology and model development. Journal of the Korean Society of Civil Engineers, Vol. 27, No. 2B, pp. 151-159.

Kim, S, Kim, H, Kay, J, and Lee, S (2015). Development and evaluation of the high resolution limited area ensemble prediction system in the Korea Meteorological Administration. Atmosphere. Korean Meteorological Society, Vol. 25: No. 1, p 67-83.


Korea Meteorological Administration (KMA) (2006). Development of monitoring and prediction technology for severe weather (heavy rainfall) over the Korea peninsula. Seoul, Korea.

Korea Meteorological Administration (KMA) (2008). Study on the weather radar application (II). Seoul, Korea.

Korea Meteorological Administration (KMA) (2012). Ensemble forecasting, forecasting technique in hand 2012. Seoul, Korea.

Lee, G, Park, K, Yu, W, Jung, K, and Jang, C (2011) A study on flood damage estimation using DEM-based flood inundation model and MD-FDA. J Korean Soc Hazard Mitig, Vol. 11, No. 5, pp. 327-336.


Leith, CE (1974) Theoretical skill of Monte Carlo forecasts. Mon Weather Rev, Vol. 102, No. 6, pp. 409-418.

Lorenz, EN (1969) Atmospheric predictability as revealed by naturally occurring analogues. J Atmos Sci, Vol. 26, No. 4, pp. 636-646.

Maltamo, M, Puumalainen, J, and P├żivinen, R (1995) Comparison of beta and weibull functions for modelling basal area diameter distribution in stands of pinus sylvestris and picea abies. Scand J For Res, Vol. 10, pp. 284-295.

Marshall, JS, and Palmer, WMK (1948) The distribution of raindrops with size. J Meteor, Vol. 5, No. 4, pp. 165-166.

Migliorini, S, Dixon, M, Bannister, R, and Ballard, S (2011) Ensemble prediction for nowcasting with a convection permitting model-I: Description of the system and the impact of radar-derived surface precipitation rates. Tellus A: Dynamic Meteorology and Oceanography, Vol. 63, No. 3, pp. 468-496.

Molteni, F, Buizza, R, Palmer, TN, and Petroliagis, T (1996) The ECMWF ensemble prediction system: Methodology and validation. Q J Royal Meteor Soc, Vol. 122, No. 529, pp. 73-119.

Mueller, C, Saxen, T, Roberts, R, Wilson, J, Betancourt, T, Dettling, S, et al (2003) NCAR auto-nowcast system. Weather and Forecasting, Vol. 18, pp. 545-561.

National Institute of Meteorological Research (NIMR) (2008). Improvement of quantitative precipitation forecast (QPF) skills in a short-range prediction (II-2). Seoul, Korea.

National Institute of Meteorological Sciences (NIMS) (2009). Development of very short-range prediction system for severe weather. Seoul, Korea.

National Weather Service (NWS) (1998). NCRFC flash flood guidance, office of hydrologic development. National Weather Service, National Oceanic and Atmospheric Administration, Silver Spring MD, USA.

Radhakrishna, B, Zawadzki, I, and Fabry, F (2012) Predictability of precipitation from continental radar images. Part V: Growth and decay. J Atmos Sci, Vol. 69, pp. 3336-3349.

Ricciardi, KL, Pinder, GF, and Belitz, K (2005) Comparison of the log-normal and beta distribution functions to describe the uncertainty in permeability. J Hydrol, Vol. 313, No. 3ŌĆō4, pp. 248-256.

Richardson, DS (2000) Skill and relative economic value of the ECMWF ensemble prediction system. Q J Royal Meteor Soc, Vol. 126, pp. 649-667.

Saito, K, Seko, H, Kawabata, T, Shoji, Y, Kuroda, T, Fujita, T, and Suzuki, O (2011). Studies at MRI toward cloud resolving ensemble NWP. Proceedings of the 11th EMS Annual Meeting. Berlin, Germany.

Seed, AW (2003) A dynamic and spatial scaling approach to advection forecasting. J Appl Meteor, Vol. 42, pp. 381-388.

Seo, BC (2010). Towards a better representation of radar-rainfall: Filling gaps in understanding uncertainties. PhD dissertation. The University of Iowa; IA, USA.

Sivillo, JK, Ahlquist, JE, and Toth, Z (1997) An ensemble forecasting primer. Weather and Forecasting, Vol. 12, No. 4, pp. 809-818.

Smith, PJ, Pappenberger, F, Wetterhall, F, Del Pozo, JT, Krzeminski, B, Salamon, P, et al (2016). On the operational implementation of the European flood awareness system (EFAS). In: Adams TE, Pagano TC, eds. Flood forecasting: A global perspective. p 313-348. Cambridge, MA, USA: Academic Press.

- TOOLS
-
METRICS

-
- 0 Crossref
- 2,415 View
- 40 Download
- Related articles in KOSHAM
-
Study on Fire Risk Assessment Method by Considering Warehouse Characteristics2020 April;20(2)
Analysis of Heavy Rain Damage Considering Regional Characteristics2018 June;18(4)