1. 서 론
수공구조물의 설계홍수량 산정을 위한 방법으로 크게 두 가지 방법이 있다. 첫 번째는 과거 홍수량 기록을 기초로 적정 홍수량을 선정하는 홍수량 기준방법이고, 두 번째는 과거 호우기록을 기초로 하여 적정 강우량을 선정한 후 강우-유출 관계분석에 따라 홍수량을 결정하는 강우량 기준방법이 다. 이와 같은 설계홍수량 산정 방법은 설계대상유역에 대한 하천유량자료의 유무에 따라 결정되며, 하천유량자료가 충분히 있을 경우 홍수량 기준방법, 하천유량자료가 없거나 미흡한 경우 강우량 기준방법을 이용한다. 일반적으로는 수공구조물 설계 시 대상유역에 대한 장기간 유출량 자료를 이용하여 설계홍수량을 산정하는 방법이 선호되어야 하지만, 유출량 자료보다 강우량 자료가 측정지점이 많고 자료 보유 연도가 길다. 또한 강우량 기준방법을 사용 시 대상유역의 첨두홍수량뿐만 아니라 수문곡선 이용하여 홍수량의 시간적 변화를 계산할 수 있기 때문에 홍수조절효과검토 등을 실시할 수 있는 이점이 있다. 이와 같은 이유로 우리나라에서는 수공구조물 설계 시 홍수량 기준방법보다 강우량 기준방법이 주로 사용되고 있다. 이러한 강우량 기준방법에서 설계강우량은 극치강우사상을 이용한 빈도해석에 기초하여, 지속시간 내의 강우총량을 결정하고 강우시간분포를 설계하는 과정을 따른다. 따라서 적합한 강우시간분포는 설계강우량을 결정하고 더 나아가 설계홍수량을 결정하는데 상당히 중요하다. 때문에 다양한 강우시간분포 방법을 분석하고 우리나라 강우 패턴에 적합한 방법을 선정할 필요가 있다.
설계강우량을 산정하기 위한 강우시간분포의 대표적인 방법으로 Huff (1967)의 Huff 4분위법, Yen and Chow (1980) 방법, 교호블록방법(Alternative Blocking Method), Mononobe 방법, SCS 곡선 방법, Keifer and Chu (1957) 방법, Pilgrim and Cordery (1975) 방법 등이 있다. 현재 국내에서는 주로 강우의 극치를 4분위로 나누어 사용자가 원하는 시간 구간에 발생시킬 수 있는 Huff 분포를 주로 이용하고 있다. 이러한 방법으로 Huff 강우분포는 강우의 시간분포를 비교적 유연하게 나타낼 수 있으나, 많은 연구를 통해 Huff 분포 방법이 특정 한계를 지닌 것을 발견하였다. 국내 연구에서는 Huff 분포 방법이 강우사상을 무차원화하여 구성하는 과정에서 다양한 기저시간의 극치강우사상 특징을 고려하기 때문에 한계가 존재하며, 이로 인해 소규모 또는 도시 유역의 첨두홍수량이 실제 첨두홍수량에 비해 낮게 산정되어 설계홍수량이 과소 추정될 수 있는 한계점을 확인하였다(Yoon et al., 2004; Jang et al., 2006a, 2006b; Choi et al., 2014). Yoon et al. (2012)과 Cho and Kim (2015)은 Huff 분포 방법의 단점을 보완하기 위해 서울 지점을 대상으로 새로운 강우 시간분포 모형을 개발하였다. 국외에서도 위와 같은 Huff 분포의 한계점에 관하여 연구가 진행되었다(Ward et al., 1980; Knapp and Terstriep, 1981; Huff, 1986, 1990). Huff 4분위법 다음으로 전진형, 중앙집중형, 지연형으로 분류되는 Mononobe 방법이 사용되는데, 이 방법은 첨두홍수량이 과대 산정되는 한계점과 첨두발생분위를 유연하게 조정하기 어려운 한계점이 있다.
위의 연구 외에도 강우시간분포를 이용한 다양한 연구가 수행되어 왔다. Horner and Jens (1942)는 Mononobe 방법과 유사하게 전방위, 중방위, 후방위로 강우시간분포를 생산하고 이를 이용해 산정한 유출량을 비교 분석하였다. Schiff (1943)와 Ogrosky (1964)도 이와 유사한 연구를 수행하였다. Yoon et al. (1998)은 도시유출모형인 ILLUDAS 모형을 산본 대상유역에 적용하여 다양한 강우분포형태에 따른 임계지속기간 및 첨두유량 변화를 분석하였다. 그 결과 첨두강우 발생위치를 비교적 쉽게 고려 가능한 방법으로 Keifer and Chu 방법과 Huff 방법이 고려되나, Keifer and Chu 방법은 총강우량이 최대강우강도의 위치에 따라 변하므로 부적절하다고 판단되어 Huff 방법을 사용하는 것이 바람직하다고 판단하였다. Lee and Lee (2003)은 시화호 유역에 관해 다양한 강우시간분포에 따른 유출특성을 비교 분석하였다. 이에 따른 결과로 Mononobe 방법을 이용했을 때 저수지 유입량이 가장 높게 나타났고, 최고저수위는 Pilgrim and Cordery 방법을 적용하였을 때 가장 높게 나타났다고 분석했다.
본 연구에서는 설계홍수량 산정을 위한 강우 시간분포로서 극치강우사상을 분석하여 집중지속시간의 특성을 반영한 HSD 방법을 제시한다. 이를 이용해 부산 지역의 집중지속시간 특성을 분석해 이를 기존의 방법들보다 잘 반영하는 강우시간분포를 산정하고자 한다. 본 연구에서 제시하는 방법은 강우지속시간에 따른 대상 기간의 연 최대 강우량 자료, 즉 극치강우사상을 선정하여 이용한다. 선정된 극치상우사상을 분석하고, 이를 기반으로 본 연구에서 제시하는 HSD 방법의 형태를 결정한다. 그리고 설계빈도에 관한 강우시간분포를 발생시키고, 이를 기존의 방법들과 비교하였다.
2. 본 론
2.1 강우시간분포 방법 개요
2.1.1 강우시간분포 대표적 방법 개요
Huff 방법은 미국 Illinois주의 유역면적 400 mi2까지 해당하는 여러 형태의 하천유역 호우를 이용해, 호우기간 중 발생한 총 강우량의 시간분포형태를 분석한 뒤, 강우시간분포 모형을 제시한 방법이다. Huff 방법은 강우지속시간을 4개의 구간으로 동일하게 나누어 어느 구간에서 강우량이 가장 많이 발생하는지에 따라 형태가 구분된다.
Mononobe 방법은 일본에서 개발된 방법으로 강우량이 집중되는 구간에 따라 전진형(Advanced Type), 중앙집중형(Centered Type), 지연형(Delayde Type)으로 나뉜다. 전진형은 임의의 시간구간인 TRLANGLE Et의 강우량이 가장 높은 순서에서 가장 낮은 순서로 차례대로 배치하는 방법이다. 이와 달리 중앙집중형은 TRLANGLE Et의 강우량 중 가장 높은 강우량을 중앙에 기준으로 두고, 다음으로 높은 강우량을 기준의 우측, 그 다음은 기준의 좌측 순으로 배치하는 방법이다. 지연형은 TRLANGLE Et의 강우량을 가장 낮은 순서에서 가장 높은 순서로 차례대로 배치하는 방법이다.
Yen and Chow 방법은 산정한 우량주상도의 형태가 삼각형과 같다고 하여 삼각형우량주상도 방법(Triangular Hyetograph Method)으로도 불린다. Yen and Chow 방법에서는 호우전진계수(Storm Advanced Coefficient)에 따라 강우시간분포 형태를 구분할 수 있다. 만약 호우전진계수가 0.5이면 설계우량주상도는 중앙집중형이 되며, 호우전진계수가 0.5보다 작으면 전진형, 0.5보다 크면 지연형이 된다.
Soil Convervation Service (SCS) 방법은 주로 미국에서 강우시간분포를 생산하기 위하여 사용 중인 방법이다. 기존의 SCS 방법은 Type Ⅰ, Ⅱ의 두가지 방법으로 강우시간분포를 생산하였으나, 이 방법의 적용성에 대한 문제가 계속 지적되었었다. 이에 따라 기존의 SCS Type Ⅰ, Ⅱ방법에서 분류를 더 세분화하여 SCS Type Ⅰ, ⅠA, Ⅱ, Ⅲ로 분류한 일명 Natural Resources Conservation Service (NRCS) 방법이 개발되었다.
2.1.2 HSD 방법 개요
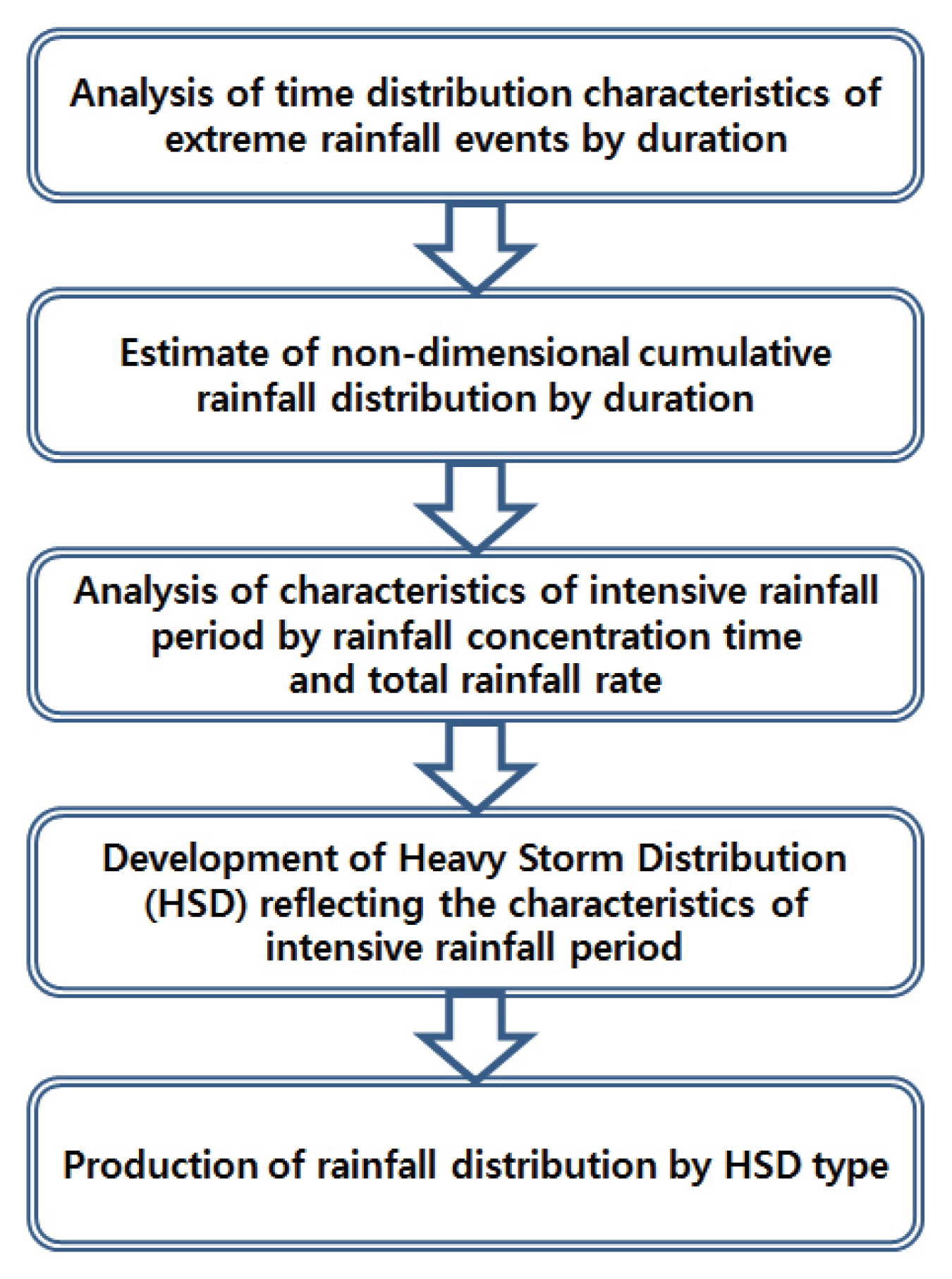
본 연구에서는 극치강우사상을 이용하여 실제 강우의 집중지속시간 특성을 반영한 강우시간분포 방법인 HSD 방법을 적용하였다(Cho and Kim, 2015). HSD 방법을 이용한 강우시간분포 구성과정은 Fig. 1과 같다. 먼저 대상 지점에 관한 강우실측자료를 구축하고 지속시간에 따른 연 최대 극치강우사상을 선정한 뒤, 무차원 확률누가곡선을 산정한다. 다음으로 선정된 극치강우사상을 이용하여 시간변화특성을 분석해 강우기간 중 약 70~80%의 강우가 집중 발생되는 집중지속시간을 파악한다. 이러한 특성들을 이용하여 대상 지점의 첨두강우 발생분위와 집중강우지속시간에 따른 HSD Type을 결정한다. 이 때 HSD Type은 A-B의 형태를 가지며, 여기서 A는 첨두강우량이 발생하는 분위, B는 집중지속시간을 의미하며 아래 Eq. (1)을 따른다.
Eq. (1)에서 B는 HSD Type 결정인자이고, tc는 과거 강우자료 분석을 통해 결정된 집중지속시간, ∆t는 강우시간분포의 시간간격을 의미한다.
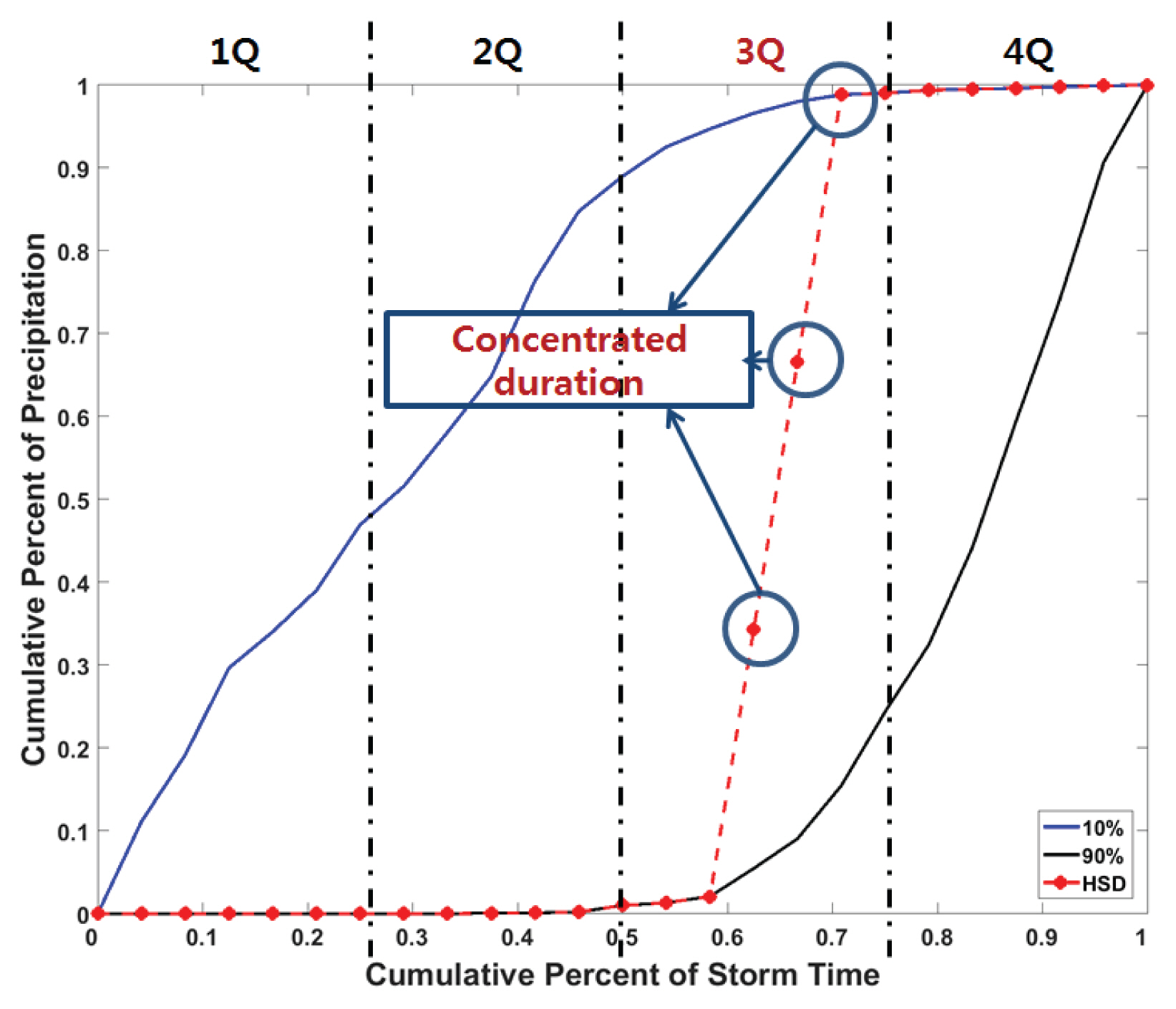
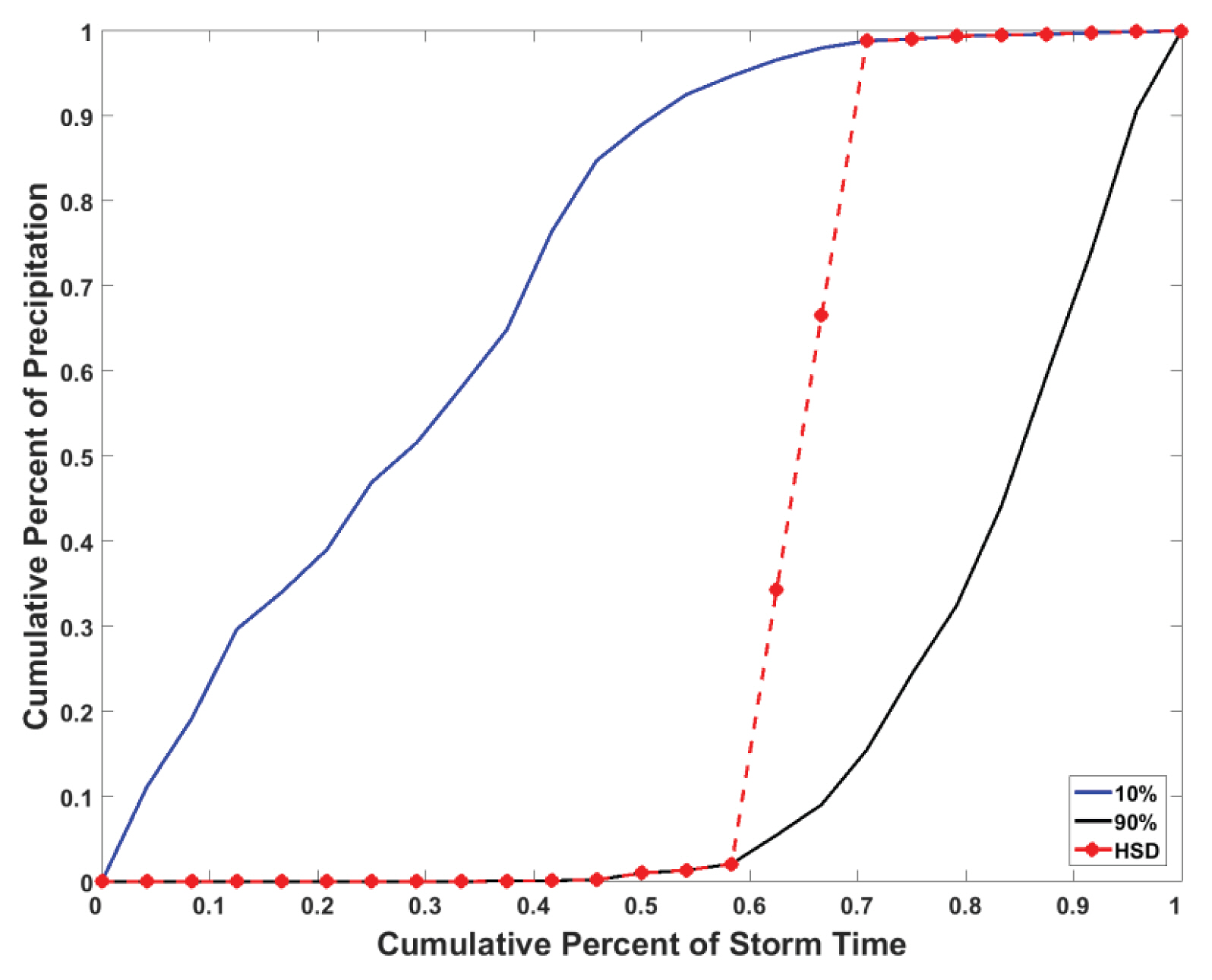
마지막으로 결정된 HSD Type에 따라 강우시간분포를 생산한다. 만약 과거 강우자료 분석을 통해 첨두강우량 발생분위가 3분위, 집중시속시간이 3시간, 시간간격이 1시간이라면 HSD Type은 3-3이고, 이에 따른 HSD 분포는 Fig. 2와 같다. 이에 따르면 과거 극치강우사상을 이용해 작성한 10%, 90% 무차원 확률곡선을 이용해 첨두강우량 발생 분위에서 집중지속시간 간격으로 선형보간을 실시하여 강우시간분포를 발생시킨다. 기존의 국내에서 주로 이용하는 Huff 방법은 50%의 무차원확률곡선을 이용하므로 강우가 평활하게 분포되는 반면, HSD 방법은 HSD Type에 따라 10%와 90%의 무차원확률곡선을 선형보간하여 강우가 일정구간에 집중되는 극치강우사상을 보다 적합하게 구현할 수 있다. 따라서 HSD 방법은 대상 지점에 대한 극치강우사상의 집중지속시간 특성을 반영하여, 첨두강우량이 낮게 산정되는 Huff 방법의 한계점을 극복할 수 있는 장점을 지닌다.
2.2 대상 지점 극치강우사상 분석
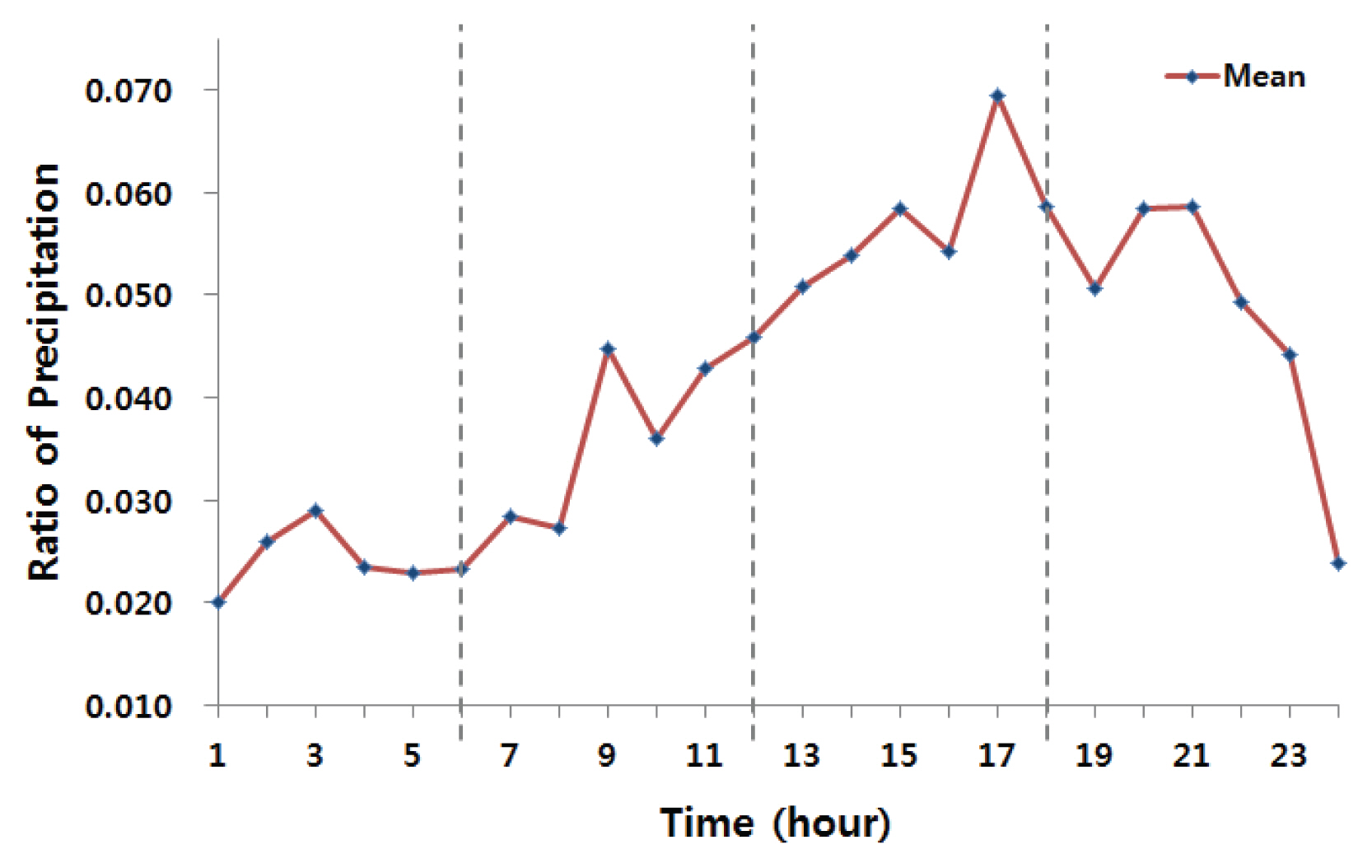
본 연구에서는 부산 지점을 대상으로 HSD 방법을 적용하여 지속시간 24시간 설계강우량을 제시하고자 한다. 이를 위해, 기상청 기상자료개방포털에서 제공하는 종관기상관측(ASOS) 자료를 이용하여 과거 57년(1961~2017년) 동안 부산 지점의 시단위 강우자료를 구축하였다. 구축한 부산 지점 시단위 강우자료를 이용하여 지속시간 24시간 연 최대강우량을 총 57개 선정하고, 이에 대한 시간변화특성을 분석하였다(Table 1). Fig. 3은 지속시간 24시간에 대한 57개 극치강우사상의 총 강우량에 대한 시간별 강우의 비율을 의미한다. 선정된 57개 극치강우사상의 분석 결과 부산 지점의 극치강우는 3분위에서 첨두강우가 발생하며, 총 강우량에 대한 강우의 비율도 3분위에서 가장 많게 나타났다. 이러한 부산 지점의 극치강우사상 분석 결과에 따라 집중지속시간을 3분위에 발생하도록 하여 설계강우량을 산정하는 것이 적정하다고 판단하였다.
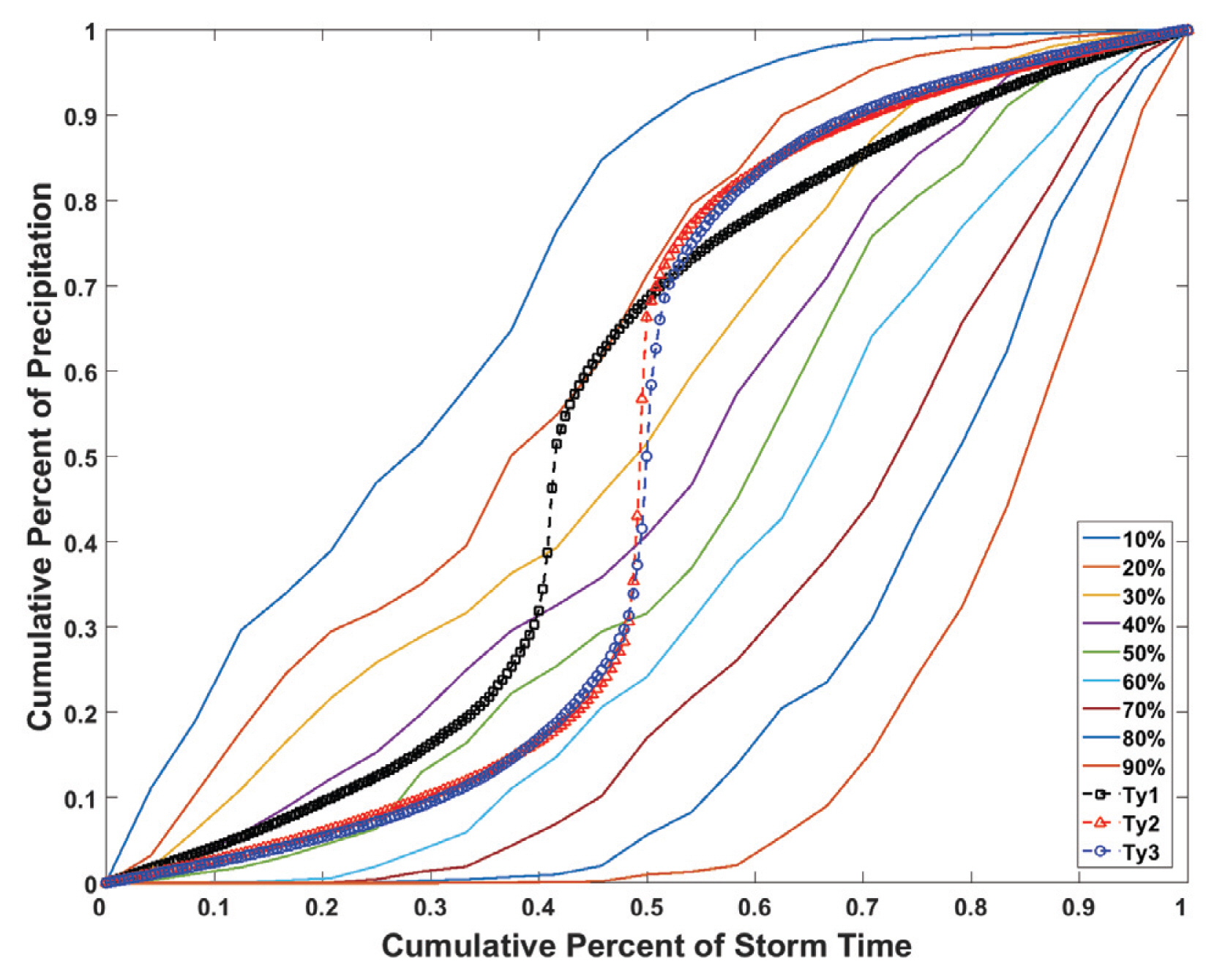
선정된 57개의 지속시간 24시간 극치강우사상을 이용하여 10%~90%의 무차원 확률누가곡선과 SCS Type I, II, III 곡선을 작성하고 비교하였다(Fig. 4). 무차원 확률누가곡선은 강우가 전체적으로 완만하게 분포되어있고, 반대로 SCS 곡선은 강우가 일정 구간에 집중되어 있다. HSD 방법은 이러한 두 방법의 특성을 연계하여 개선된 강우시간분포를 제시하여, 조금 더 현실강우사상에 적합한 설계강우량을 산정하고자 한다.
이를 위하여 부산 지점의 극치강우사상에 대한 집중강우특성을 분석하였다. 선정된 57개의 24시간 극치강우사상에 대해 집중지속시간 1시간, 2시간, 3시간별 강우의 첨두량 발생 분위를 분석하였다(Table 2). 분석 결과 첨두강우 발생빈도는 주로 3분위, 4분위에서 발생하였으며, 이 중에서도 3분위에서 38.6%로 가장 높게 나타났다. 따라서 Fig. 3과 Table 2를 근거로 부산 지역의 HSD 방법 적용 시 3분위에서 첨두강우가 발생하도록 결정하였다.
집중지속시간을 결정하기 위하여 선정된 57개 극치강우사상 총 강우량에 대한 지속시간 1시간, 2시간, 3시간별 첨두강우량의 비율을 분석하였다(Table 3). Largest는 57개 중 가장 높은 비율 1개를 의미하고, Top 5%, Top 10%, Top 15%는 각각 57개 중 상위 3개, 상위 6개, 상위 9개의 평균 비율을 나타낸다. 이에 따르면 지속시간이 1시간에서 3시간으로 증가함에 따라 첨두강우량의 비율도 증가하며, 지속시간이 3시간일 때 최고치는 0.82, 상위 5%의 평균 비율은 0.78로 높은 비율을 나타냈다. 본 연구에서는 강우기간 중 약 70%~80%의 강우가 집중되는 구간을 집중지속시간으로 정의하여 HSD 방법을 적용하고자 하므로, Table 3을 근거로 집중지속시간을 3시간으로 결정하였다.
2.3 HSD 방법 적용 및 평가
본 연구에서는 과거 57년(1961~2017)의 부산 지점 극치강우사상 분석을 통해 HSD 방법 적용을 위한 첨두강우 발생분위를 3분위로 결정하였다. 그리고 극치강우사상 중 본 연구에서 목표로 하는 약 70%~80%의 강우가 집중되는 집중지속시간을 3시간으로 결정하였다. 이에 따라 HSD Type A-B에서 A는 3, B는 Eq. (1)에서 ∆t는 1시간, tc는 3시간이므로 3으로 결정되었다. 즉 HSD Type 3-3으로 결정되었다.
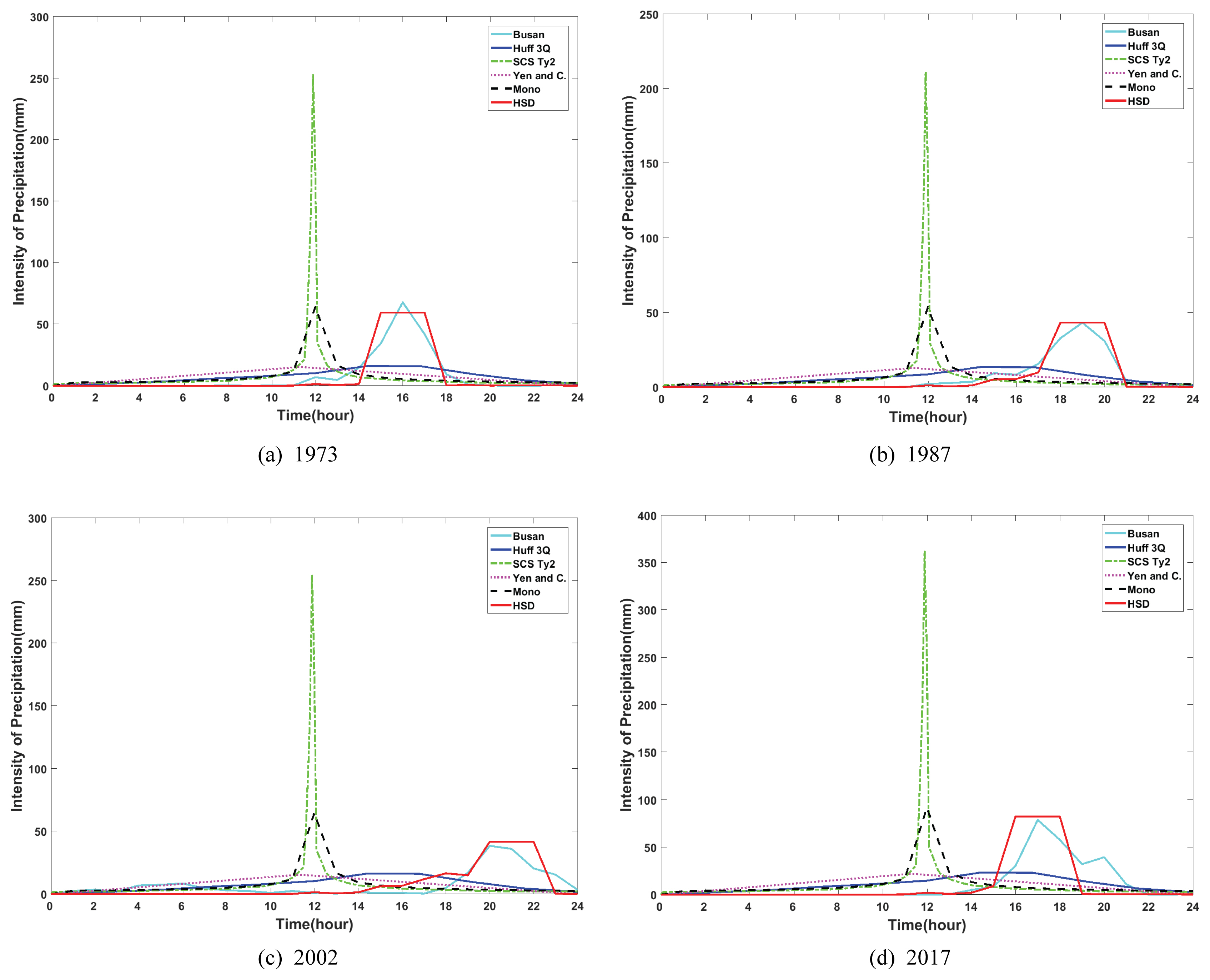
Fig. 5는 부산 지점의 본 연구에서 제시하는 3분위에서 극치가 발생하고 집중지속시간이 3시간인 HSD Type 3-3 방법의 무차원 확률 누가곡선을 나타낸다. 이는 HSD 방법의 과정으로 10%, 90%의 무차원 확률곡선을 HSD Type에 따라 선형보간을 실시한 결과이다. 본 연구에서 제시하는 HSD 방법의 적용성을 평가하기 위하여 실제 부산 지점 강우량과 여러 강우분포방법으로 생산한 설계강우량을 비교하였다(Fig. 6). 제시한 샘플은 각각 Figs. 6(a)부터 6(d) 순으로 1973년, 1987년, 2002년, 2017년의 부산 지점 실제 강우량을 이용한 결과이다. 이 때 HSD Type은 해당 연도의 부산 지점의 실제 극치강우에 따라 (a)와 (d)의 경우 Type 3-3을 이용하였으며, HSD Type (b)와 (c)는 Type 4-3을 이용하였다. 부산 지점의 해당 년도의 강우를 이용해 Huff 방법, SCS 방법, Yen and Chow 방법, Mononobe 방법을 실시하고, 본 연구에서 제시하는 HSD 방법과 비교 분석하였다. 그 결과 Huff 방법은 실제 강우보다 첨두강우량이 낮게 산정되어 집중강우특성을 제대로 반영하기 힘든 한계점이 보였다. 이는 Huff 방법은 무차원 확률곡선 산정 시에 확률곡선을 비교적 완만하게 산정하기 때문에, 이에 따른 강우시간분포 또한 평활하게 산정되기 때문이다. SCS 곡선 방법은 반대로 집중강우특성은 나타나지만 극치의 발생 위치 및 지속시간이 실제 강우와 비교 시 적합하지 못하다고 판단된다. 이는 Fig. 4에서 알 수 있듯이 SCS 방법의 확률곡선은 일정구간에 급격하게 증가하기 때문에 첨두강우량 또한 과도하게 산정되기 때문이다. Yen and Chow 방법 또한 집중강우특성을 반영하는데 한계를 보인다. 이는 Huff 방법과 비슷하게 강우의 확률분포가 비교적 평활하게 생산되기 때문이다. Mononobe 방법은 강우의 첨두값은 실제 강우와 비슷하게 산정되었으나 지속시간과 극치의 발생 위치가 실제 강우에 비해 적합성이 떨어진다고 판단되었다. 이는 Mononobe 방법의 특성상 형태가 3가지로 고정되어 있어 첨두강우의 발생위치를 유연하게 조정하기 어렵기 때문이다. HSD 방법은 강우의 집중지속시간을 조절할 수 있는 점, 극치발생 위치 또한 유연하게 조정이 가능한 점 등의 장점을 통해 기존의 방법들보다 극치강우사상에 보다 적합한 강우시간분포를 생산한다고 판단되었다.
2.4 HSD 방법을 이용한 설계강우량 산정
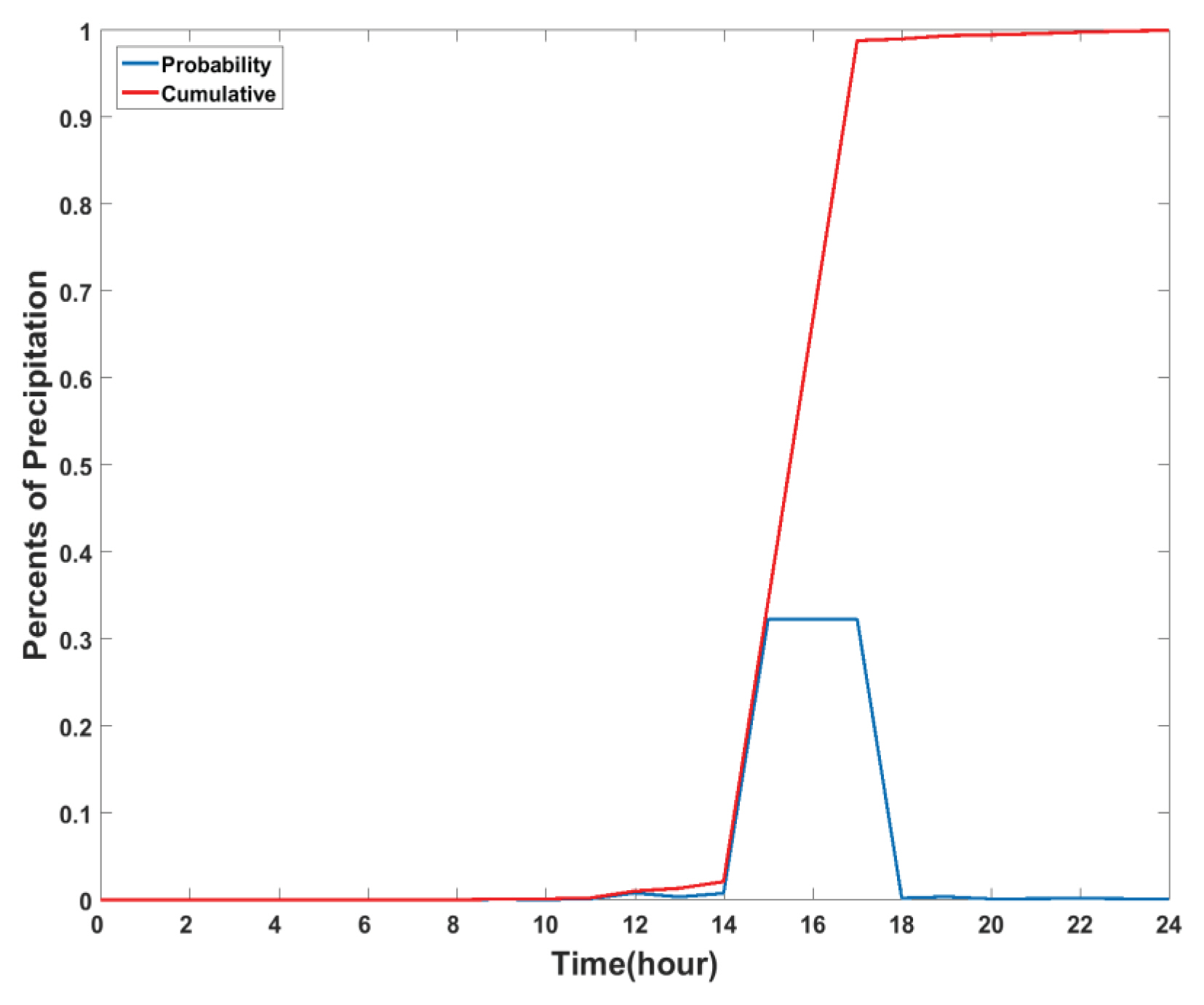
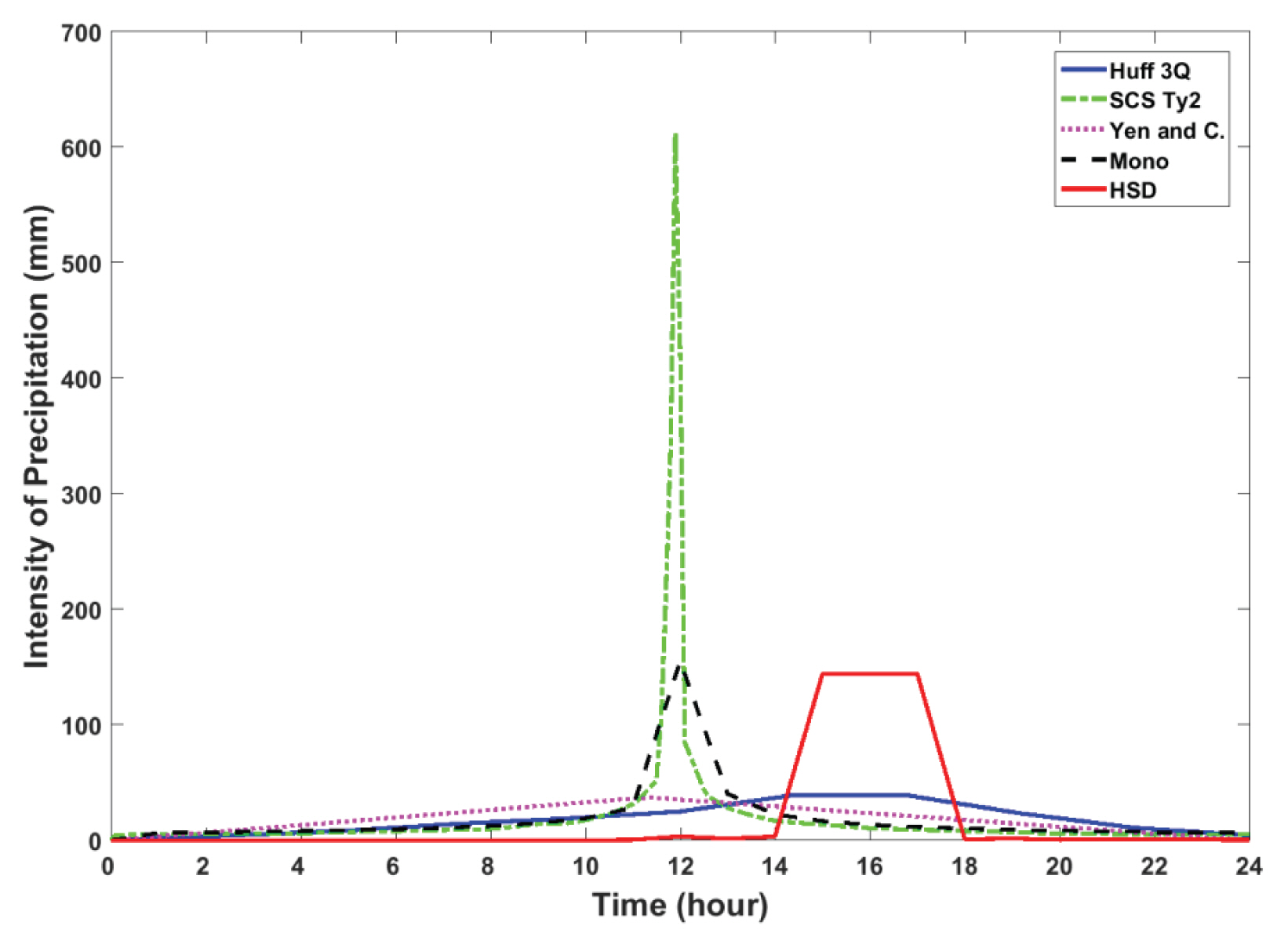
본 연구에서 HSD Type3-3 방법을 이용한 부산 지점의 지속시간 24시간에 대한 강우시간분포 확률곡선과 누가확률곡선은 Fig. 7과 같으며, 강우의 극치는 3분위에서 발생하고, 집중지속시간은 3시간으로 설정하였다. 이를 이용하여 부산 지점의 200년 빈도 지속시간 24시간 설계강우량을 산정하고, Huff 방법, SCS 방법 등을 이용한 설계강우량과 비교하였다(Fig. 8). 이에 따르면 위에서 분석했던 것과 같이 Huff 방법과 Yen and Chow 방법은 설계강우량을 비교적 평활하고 과소 추정하는 한계점이 드러났으며, SCS 방법은 강우가 과도하게 일부시간에 집중되는 한계점이 나타났다. Mononobe 방법은 강우의 극치발생위치와 집중강우지속시간을 유연하게 설정하기 어려운 한계점이 있었다. 이에 반해 본 연구에서 제시하는 HSD 방법은 극치강우사상의 집중강우특성을 반영함으로써 Huff 방법의 한계점을 극복하면서 극치의 발생위치를 유연하게 설정하고, 집중지속시간을 조절할 수 있는 강점을 보였다.
3. 결 론
수공구조물의 설계 시 설계홍수량 결정을 위하여 홍수량 기준방법 또는 강우량 기준방법을 이용한다. 하천유량자료가 없거나 미흡한 경우 강우량 기준방법을 이용하는데, 일반적으로 유출량 자료보다 강우량 자료가 측정지점이 많고 자료 보유 연도가 길어, 수공구조물 설계 시 강우량 기준방법이 주로 사용된다. 이러한 강우량 기준방법에서 적합한 강우시간분포는 설계강우량을 산정하고, 설계홍수량을 결정하는데 상당히 중요한 영향을 미친다. 그렇기 때문에 다양한 강우시간분포 방법을 분석하고 적합한 강우시간분포 방법을 선정하는 것은 매우 중요하다. 본 연구에서는 Huff 방법이 극치강우사상에 대한 집중지속시간 특성을 제대로 반영하지 못한다는 한계점을 보완하고, 극치강우사상의 지속시간에 대한 첨두강우 발생분위와 집중지속시간 특성을 반영하는 새로운 강우시간분포 방법인 HSD 방법을 제시하였다. 이를 이용해 부산 지점의 극치강우 시간분포 특성을 보다 잘 반영하는 설계강우량을 산정하고 기존의 방법들과 비교하였다.
HSD 방법을 적용하기 위하여 부산 지점의 57년간 강우 실측자료를 이용해 57개의 극치강우사상을 산정하였다. 그리고 이를 분석하여 부산 지점의 첨두강우 발생분위 빈도를 파악하고 집중지속시간을 결정하고, 이를 토대로 HSD Type을 결정하였다. 위 과정을 통하여 결정된 부산 지점의 HSD Type은 3-3이고, 첨두강우의 발생분위는 3분위, 집중강우지속시간은 3시간으로 결정되었다. HSD 방법의 적용성을 평가하기 위해 1973년, 1987년, 2002년, 2017년에 대한 강우시간분포 샘플을 제시했으며, 그 결과를 Huff 방법, Yen and Chow 방법, SCS 방법 등과 비교했을 때 HSD 방법이 실제 부산 지점의 극치강우사상에 더 적합하다고 판단되었다.
부산 지점의 설계빈도 200년에 관하여 HSD 방법과 기존의 방법들을 이용한 설계강우량을 비교 분석하였다. 이을 통하여 보다 개선된 설계강우량 산정 방법의 필요성을 제시하였다. 본 연구를 통해 수공구조물의 설계홍수량 산정을 위한 강우시간분포의 방법으로 현재 사용 중인 여러 방법들의 한계점을 파악할 수 있었다. 그리고 본 연구에서 적용한 HSD 방법은 이러한 한계점들을 극복하고 우리나라 극치강우 시간분포 특성에 적합한 강우시간분포 생산이 가능할 것으로 판단하였다.
PDF Links
PubReader
ePub Link
Full text via DOI
Download Citation
Print
