1. ņä£ļĪĀ
Ļ░ĢņÜ░ņŚÉ ņØśĒĢ£ ļ¼╝ņØś ņØ┤ļÅÖņØĆ ļīĆĻĖ░ ņ”Øļ░£(evaporation), ņ¦Ćļ░ś ņ╣©Ēł¼(infiltration), ĻĘĖļ”¼Ļ│Ā ņ¦ĆĒæ£ļ®┤ ņ£ĀņČ£(surface runoff)ļĪ£ ĻĄ¼ļČäĒĢĀ ņłś ņ׳ļŗż. ĒŖ╣Ē׳ ņ¦Ćļ░ś ņ╣©Ēł¼ņÖĆ ņ¦ĆĒæ£ļ®┤ ņ£ĀņČ£ņØĆ ņłśļ”¼ĒĢÖņĀü Ļ┤ĆņĀÉņŚÉņä£ ļ¦żņÜ░ ļ░ĆņĀæĒĢśĻ▓ī ņāüĒśĖ ņŚ░Ļ┤ĆļÉ£ ĒśäņāüņØ┤ļŗż. ņ¦Ćļ░ś ņ╣©Ēł¼ņŚÉ ņØśĒĢ£ ņ¦ĆĒæ£ļ®┤ņØś ņØīņØś Ļ░äĻĘ╣ņłśņĢĢ(suction)ņØś Ļ░ÉņåīļŖö ļČłĒżĒÖö ņ¦Ćļ░śņØś ņĀäļŗ©Ļ░ĢļÅäļź╝ Ļ░Éņåīņŗ£ņ╝£ ņé¼ļ®┤ņØś ņĢłņĀĢņä▒ņØä ņĀĆĒĢ┤ņŗ£Ēéżļ®░, Ēæ£ļ®┤ ņ£ĀņČ£ņØĆ ņłśļ¼ĖĒĢÖņŚÉņä£ ĒĢśņłś Ļ┤ĆĻ▒░ ņŗ£ņäżņØś ņŻ╝ņÜö ņäżĻ│ä ņØĖņ×ÉņØ┤ļŗż. ņØ┤ļ¤¼ĒĢ£ Ļ░ĢņÜ░ņŚÉ ņØśĒĢ£ ņ¦Ćļ░ś ņ╣©Ēł¼ņÖĆ Ēæ£ļ®┤ ņ£ĀņČ£ņØś ņāüĒśĖņ×æņÜ®ņØĆ ļ│Ąņ×ĪĒĢ£ ņ¦ĆĒśĢņĪ░Ļ▒┤Ļ│╝ ļŗżņ¢æĒĢ£ ņ¦Ćļ░śņĪ░Ļ▒┤ņØä ĒåĄĻ│╝ĒĢśļŖö Ļ▓ĮņÜ░ ļŹöņÜ▒ ļ│Ąņ×ĪĒĢ£ ņ¢æņāüņØä ļØĀĻ▓ī ļÉ£ļŗż.
ĻĖ░ņĪ┤ņØś ļīĆļČĆļČä ņłśļ”¼ĒĢ┤ņäØņØĆ ņ¦Ćļ░ś ņ╣©Ēł¼ņÖĆ ņ¦ĆĒæ£ļ®┤ ņ£ĀņČ£ņØś ņāüĒśĖņ×æņÜ®ņØä Ļ│ĀļĀżĒĢśņ¦Ć ļ¬╗ĒĢśĻ│Ā, ĒĢ£ ļČĆļČäņØ┤ ņØ╝ņĀĢĒĢśļŗżĻ│Ā Ļ░ĆņĀĢĒĢśĻ▒░ļéś Ļ▓ĮĒŚśņŗØņØä ņØ┤ņÜ®ĒĢśņŚ¼ ļæÉ ĒśäņāüņØś ņāüĒśĖ ņ×æņÜ®ņØä ļ¼┤ņŗ£ĒĢśņśĆļŗż (
Hwang, 2015). ĒŖ╣Ē׳, ņłśļ¼ĖĒĢÖņŚÉņä£ļŖö ņ¦Ćļ░ś ņ╣©Ēł¼ļŖźņØä ņé░ņĀĢĒĢśĻĖ░ ņ£äĒĢśņŚ¼ Ļ▓ĮĒŚśņĀüņØĖ Horton ļ¬©ļŹĖ, Philip ļ¬©ļŹĖ, Green-Ampt ļ¬©ļŹĖ ļō▒ņØä ņé¼ņÜ®ĒĢśĻ│Ā ņ׳ņ£╝ļ®░, ņ£ĀņČ£ļ¤ēņØä ņé░ņĀĢĒĢśĻĖ░ ņ£äĒĢśņŚ¼ NRCS ļ¬©ļŹĖļĪ£ļČĆĒä░ Ļ░ĢņÜ░ņŚÉ ņØśĒĢ£ ņ╣©Ēł¼ņØś ņŗ£Ļ░äņĀüņØĖ ļ│ĆĒÖöļź╝ ņé░ņĀĢĒĢśĻ│Ā ņ׳ļŗż(
Lee, 2015). ļ░śļ®┤ ņ¦Ćļ░śĻ│ĄĒĢÖņŚÉņä£ļŖö ņØ╝ļ░śņĀüņ£╝ļĪ£ ņé¼ņÜ®ĒĢśļŖö ļ▓öņÜ®ĒöäļĪ£ĻĘĖļש ļō▒ņŚÉņä£ ņ¦ĆĒæ£ļ®┤ ņ£ĀņČ£ņØä ļ¼┤ņŗ£ĒĢśĻ│Ā Ļ░ĢņÜ░ņŚÉ ņØśĒĢ£ ņ£Āļ¤ēņØä ņ¦ĆĒæ£ļ®┤ņŚÉ ņ¦üņĀæ ņŻ╝ņ×ģĒĢśņŚ¼ ĒĢ┤ņäØņØä ņłśĒ¢ēĒĢśņśĆļŗż. ĒĢśņ¦Ćļ¦ī ņŗżņĀ£ ņ¦Ćļ░ś ņ╣©Ēł¼ņÖĆ ņ¦ĆĒæ£ļ®┤ ņ£ĀņČ£ļ¤ēņØś ļ╣äņ£©ņØĆ ņ¦Ćļ░śņØś ļČłĒżĒÖö ņłśļ”¼ĒĢÖņĀü ņĪ░Ļ▒┤, ņ¦ĆĒæ£ļ®┤ ĒśĢņāü, ņäĀĒ¢ēĻ░ĢņÜ░ņŚÉ ņØśĒĢ£ ņ┤łĻĖ░ Ļ░äĻĘ╣ņłśņĢĢ ļō▒ ļŗżņ¢æĒĢ£ ņÜöņØĖļōżņŚÉ ņØśĒĢśņŚ¼ Ļ▓░ņĀĢļÉ£ļŗż. ņśłļź╝ ļōżļ®┤, ĻĖēĻ▓Įņé¼, ņŖĄņ£ż ņāüĒā£ņØś ņ¦Ćļ░ś, ņ¢æĒśĖĒĢ£ ņ¦Ćļ░ś Ēö╝ļ│Ą ņĪ░Ļ▒┤ ļō▒ņŚÉņä£ ņ¦ĆĒæ£ļ®┤ ņ£ĀņČ£ļ¤ēņØ┤ ņāüļīĆņĀüņ£╝ļĪ£ ņ”ØĻ░ĆĒĢśĻ▓ī ļÉ£ļŗż.
ņ¦Ćļ░śņØś ņłśļ”¼ĒĢÖņĀü ĒĢ┤ņäØņŚÉņä£ ņŻ╝ ļ│ĆņłśļŖö Ļ░äĻĘ╣ņłśņĢĢņØ┤ļ®░, Ļ▓ĮĻ│äņĪ░Ļ▒┤ņØĆ ņĀłņĀÉņØś Ļ░äĻĘ╣ņłśņĢĢņØä ņ¦üņĀæ ņ¦ĆņĀĢĒĢśļŖö Essential (Dirichlet) Ļ▓ĮĻ│äņĪ░Ļ▒┤Ļ│╝ Ļ░äĻĘ╣ņłśņĢĢņØś Ļ│ĄĻ░äņĀü ĻĖ░ņÜĖĻĖ░ņØĖ ņ£Āļ¤ēņØä ņ¦ĆņĀĢĒĢśļŖö Non-essential (Neumann) Ļ▓ĮĻ│äņĪ░Ļ▒┤ņØ┤ ņ׳ļŗż. ĻĘĖļ”¼Ļ│Ā ņ£ĀĒĢ£ņÜöņåīļ▓ĢņŚÉņä£ ņ£Āļ¤ēĻ│╝ Ļ░ÖņØĆ Nuemann Ļ▓ĮĻ│äņĪ░Ļ▒┤ņØĆ ņłśņ╣ś ĒĢ┤ņäØņĀü ļČłņĢłņĀĢņä▒ņØä ņ┤łļלĒĢĀ ņłś ņ׳ļŗż. ņŚ┤ņĀü ļ¼ĖņĀ£(
Thomas and Zhou, 1997)ļéś ņłśļ”¼ĒĢÖņĀü ļ¼ĖņĀ£(
Phoon et al., 2007)ņŚÉņä£ ņØ┤ļ¤¼ĒĢ£ ļČłņĢłņĀĢņä▒ņØä ņÖäĒÖöĒĢśĻĖ░ ņ£äĒĢ£ ņĄ£ņåī ņŗ£Ļ░ä Ļ░äĻ▓®ņØ┤ļéś, ņØĖņ£äņĀüņØĖ ņÖäĒÖö ĻĖ░ļ▓ĢņŚÉ ļīĆĒĢśņŚ¼ ļģ╝ņØśļÉśņŚłļŗż. ņØ┤ļŖö Laplace ĒśĢĒā£ņØś ņ¦Ćļ░░ļ░®ņĀĢņŗØņØä strong formņØ┤ ņĢäļŗī weak formņØś ĒśĢĒā£ļź╝ ņé¼ņÜ®ĒĢśļŖö Galerkin ņłśņŗØĒÖöņŚÉ ņØśĒĢ£ Ļ▓āņØ┤ļ®░, ņłśņ╣śņĀü ļČłņĢłņĀĢņä▒ņØĆ ņŻ╝ņ¢┤ņ¦ä ņłśļ”¼ĒĢÖņĀü Ēś╣ņØĆ ņŚ┤ņĀü ņ£Āļ¤ēņØ┤ Ēü¼ĻĖ░Ļ░Ć ņ¦Ćļ░ś ņÜ®ļ¤ēļ│┤ļŗż ņ╗żņ¦Ćļ®┤ ļ░£ņāØĒĢ£ļŗż. ļö░ļØ╝ņä£ ņØ╝ļČĆ ļ▓öņÜ®ĒöäļĪ£ĻĘĖļשņØĆ ņ¦Ćļ░śņØś ņ╣©Ēł¼ ņÜ®ļ¤ē(infiltration capacity)ņØä ņ┤łĻ│╝ĒĢśļŖö ņ£Āļ¤ēņØĆ ļ¼┤ņŗ£ĒĢśĻ│Ā ņØĖņ£äņĀüņ£╝ļĪ£ ĒĢ┤ņäØĻ▓░Ļ│╝ļź╝ ņĪ░ņĀĢĒĢśņŚ¼ ņĢłņĀĢņä▒ņØä ņ£Āņ¦ĆĒĢśĻĖ░ļÅä ĒĢ£ļŗż(
Karthikeyan et al., 2001).
ņØ┤ļ¤¼ĒĢ£ ņłśņ╣śĒĢ┤ņäØ ĻĖ░ļ▓ĢņØĆ Ļ░ĢņÜ░ņŚÉ ņØśĒĢ£ ņ¦ĆĒæ£ļ®┤ ņ£ĀņČ£Ļ│╝ ņ¦Ćļ░ś ņ╣©Ēł¼ņØś ņŚ░Ļ│äļÉ£ ĒśäņāüņØä Ļ│ĀļĀżĒĢśņ¦Ć ņĢŖņĢäņä£ ļ░£ņāØĒĢśļŖö ņłśņ╣ś ĒĢ┤ņäØņĀü ļ¼ĖņĀ£ņØ┤ļŗż. ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö ĻĖ░ņĪ┤ņØś ņ£ĀĒĢ£ ņ░©ļČäļ▓ĢņØ┤ļéś ņ£ĀĒĢ£ ņ▓┤ņĀüļ▓Ģņ£╝ļĪ£ ņłśĒ¢ēĒĢśņśĆļŹś ņ¦ĆĒæ£ļ®┤ ņ£ĀņČ£Ļ│╝ ņ¦Ćļ░ś ņ╣©Ēł¼ ņŚ░Ļ│äĒĢ┤ņäØņØä ņ£ĀĒĢ£ ņÜöņåīļ▓ĢņŚÉņä£ ņłśĒ¢ēĒĢśĻĖ░ ņ£äĒĢ£ ņĢłņĀĢĒÖö ĻĖ░ļ▓ĢņØä ņĀ£ņĢłĒĢśĻ│Ā, ņØ┤ļź╝ ņØ┤ņÜ®ĒĢśņŚ¼ 1ņ░©ņøÉ ņ╣©Ēł¼-Ļ│Āņ×ä ĒĢ┤ņäØĻ│╝ ņé¼ļ®┤ņØś Ļ░ĢņÜ░ņŚÉ ņØśĒĢ£ ņ╣©Ēł¼-ņ£ĀņČ£ ĒĢ┤ņäØņØä ņłśĒ¢ēĒĢśĻ│Āņ×É ĒĢ£ļŗż.
2. ņ¦ĆĒæ£ļ®┤-ņ¦Ćņżæ ņ£Āņ▓┤ ĒØÉļ”äņŚÉ ņ¦Ćļ░░ļ░®ņĀĢņŗØ
ņ¦ĆņżæņØś ņ¦ĆĒĢśņłś ĒØÉļ”ä ĒĢ┤ņäØņØĆ ļŗżĻ│Ąņ¦ł ļé┤ ņ£Āņ▓┤ ĒØÉļ”äņŚÉ ļīĆĒĢ£ ņ¦Ćļ░░ ļ░®ņĀĢņŗØņØä ņĀüņÜ®ĒĢśņśĆļŗż. ĻĘĖļ”¼Ļ│Ā ņ¢ĢņØĆ ņ¦ĆĒæ£ļ®┤ ĒØÉļ”ä(shallow overland flow)ņØĆ St. Venant ļ░®ņĀĢņŗØņ£╝ļĪ£ ņĢīļĀżņĀĖ ņ׳ļŖö ņ¢ĢņØĆ ļ¼╝ņØś ĒØÉļ”ä ļ░®ņĀĢņŗØņØä ņé¼ņÜ®ĒĢśņśĆļŗż. ĻĘĖļ”¼Ļ│Ā ņ¦ĆĒæ£ļ®┤ ĒØÉļ”äĻ│╝ ņ¦Ćņżæ ņ¦ĆĒĢśņłś ĒØÉļ”äņØś ņāüĒśĖņ×æņÜ®ņØĆ ņ¦Ćļ░ś ņ╣©Ēł¼ ĒśĢņŗØņ£╝ļĪ£ ļ¬©ļŹĖļ¦üĒĢśņśĆļŗż.
2.1 ņ¦ĆĒæ£ļ®┤ ņ£ĀņČ£ņŚÉ ļīĆĒĢ£ ņ¦Ćļ░░ļ░®ņĀĢņŗØ
ļ¼╝ņ¦łņØś ņØ┤ļÅÖņŚÉ ļīĆĒĢ£ Ļ▒░ņŗ£ņĀüņØĖ ĒÄĖļ»ĖļČä ĒÅēĒśĢļ░®ņĀĢņŗØņØĆ
╬┤ŽüŽł/
╬┤t+Ōłć┬Ę
jŽł=
fŽł(
Shin, 2011)Ļ│╝ Ļ░Öņ£╝ļ®░, ņØ┤ļź╝ ņ¦ĆĒæ£ļ®┤ ĒØÉļ”äņŚÉ ņĀüņÜ®ĒĢśļ®┤ ļŗżņØīĻ│╝ Ļ░ÖņØĆ ņØ╝ļ░śĒÖöļÉ£ ņ¦ĆĒæ£ļ®┤ ņ£ĀņČ£ ĒØÉļ”äļ░®ņĀĢņŗØņØä ņ¢╗ņØä ņłś ņ׳ļŗż.
ņŚ¼ĻĖ░ņä£, hļŖö ņ¦ĆĒæ£ļ®┤ ņ£ĀņČ£ Ļ╣ŖņØ┤ (surface runoff water depth)ņØ┤ļ®░, uxņÖĆ uyļŖö ņ¦ĆĒæ£ļ®┤ ņ£ĀņČ£ņłśņØś ĒØÉļ”äņåŹļÅäņØ┤ļŗż. RļŖö Ļ░ĢņÜ░ Ļ░ĢļÅä(rainfall intensity)ļź╝ ļéśĒāĆļé┤ļ®░, IļŖö ņ¦ĆĒæ£ļ®┤ ņ£ĀņČ£ņłśņØś ņ¦Ćņżæņ£╝ļĪ£ ņ╣©Ēł¼ ņåŹļÅä(infiltration rate)ļź╝ ļéśĒāĆļéĖļŗż.
ņ¦ĆĒæ£ļ®┤ņŚÉņä£ ņ£ĀņČ£ ņåŹļÅäļŖö ManningņØś ļ¦łņ░░ ĒØÉļ”äņŚÉ ļīĆĒĢ£ Ļ▓ĮĒŚśņŗØņØä ņĀüņÜ®ĒĢśņśĆļŗż.
ņŚ¼ĻĖ░ņä£, nņØĆ ManningņØś Ļ▒░ņ╣ĀĻĖ░ Ļ│äņłś [s/m1/3]ņØ┤ļ®░, ņ¦ĆĒśĢĻ▓Įņé¼ļŖö S0=Sx2+Sy2ņ£╝ļĪ£
Sx=ŌłÆ╬┤(z+h)/╬┤xĻ│╝Sy=ŌłÆ╬┤(z+h)/╬┤yņ£╝ļĪ£ Ēæ£ĒśäĒĢĀ ņłś ņ׳ļŗż.
Eq. (1)ņŚÉņä£ ņ¦ĆĒæ£ļ®┤ ņ£ĀņČ£ ņåŹļÅäļŖö ļŗżņØīĻ│╝ Ļ░ÖņØ┤ ņĀĢļ”¼ĒĢĀ ņłś ņ׳ļŗż.
ņŚ¼ĻĖ░ņä£ KIļŖö ņ¦ĆĒæ£ļ®┤ņŚÉņä£ ņ¦Ćņżæņ£╝ļĪ£ņØś ļłäņČ£Ļ│äņłś (leakage coefficient)ņØ┤ļŗż.
ņØ┤ļź╝ ņĀĢļ”¼ĒĢśņŚ¼ ņ¦ĆĒæ£ļ®┤ ņ£ĀņČ£ņŚÉ Ļ┤ĆĒĢ£ ņ¦Ćļ░░ ļ░®ņĀĢņŗØņØĆ ļŗżņØīĻ│╝ Ļ░ÖņØ┤ ņĀĢļ”¼ĒĢĀ ņłś ņ׳ļŗż.
ņŚ¼ĻĖ░ņä£ H=z+hļŖö Ēæ£ļ®┤ ņ£ĀņČ£ ĒØÉļ”äņØś ņĀäņłśļæÉņØ┤ļ®░, ņ¦Ćļ░░ļ░®ņĀĢņŗØņØś ļ¦żĻ░£ļ│ĆņłśļŖö bi=23ui, ╬║i=hV0S0ŌłÆ12huiS0SiS0ņÖĆ Ļ░Öļŗż.
ņ¦ĆĒæ£ļ®┤ ņ£ĀņČ£ņŚÉ Ļ┤ĆĒĢ£ ņ£ĀļÅÖ ņŚŁĒĢÖņĀü ļ░®ņĀĢņŗØ (Eq. (5))ņØś ņłśļĀ┤ņä▒Ļ│╝ ņĢłņĀĢņä▒ņØä Ē¢źņāüņŗ£ĒéżĻĖ░ ņ£äĒĢśņŚ¼ Consistent Petrov-Galerkin ņłśņŗØĒÖöļź╝ ņĀüņÜ®ĒĢśņśĆļŗż(
Zienkiewicz et al., 2005).
ņŚ¼ĻĖ░ņä£ p(Žē)=bi╬┤wi/╬┤xiņØ┤ļ®░, Žä=╬öt/2 ņØä ņĀüņÜ®ĒĢśņśĆļŗż.
2.2 ļČłĒżĒÖö ņ¦Ćļ░śņŚÉ ļīĆĒĢ£ ņłśļ”¼ĒĢÖņĀü ņ¦Ćļ░░ļ░®ņĀĢņŗØ
ņ¦ĆņżæņØś ļČłĒżĒÖö/ĒżĒÖö ņ¦Ćļ░śņŚÉ ļīĆĒĢ£ ļ¼╝ņØś ĒØÉļ”äņØĆ RichardņØś ļ░®ņĀĢņŗØņØä ņĢīļĀżņĀĖ ņ׳ļŖö ņŚ░ņåŹļ░®ņĀĢņŗØņŚÉ Ļ░ĢņÜ░ņØś ņ¦Ćņżæ ņ╣©Ēł¼ņŚÉ ņØśĒĢśņŚ¼ ņ£Āņ×ģļÉ£ ļ¼╝ņØä Ļ│ĀļĀżĒĢśņŚ¼ ņ¦łļ¤ēļ│┤ņĪ┤ņØś ļ▓Ģņ╣ÖņŚÉ ļīĆĒĢ£ ņ¦Ćļ░░ļ░®ņĀĢņŗØņØä ņ£ĀļÅäĒĢśņśĆļŗż. ņ¦Ćļ░░ ļ░®ņĀĢņŗØņŚÉ Galerkin ņłśņŗØĒÖöļź╝ ņĀüņÜ®ĒĢśņŚ¼ ļŗżņØīĻ│╝ Ļ░ÖņØĆ Ļ░ĢņÜ░ ņ╣©Ēł¼ļź╝ Ļ│ĀļĀżĒĢ£ ļ░®ņĀĢņŗØņ£╝ļĪ£ ņĀĢļ”¼ĒĢĀ ņłś ņ׳ļŗż.
ņŚ¼ĻĖ░ņä£ ļŗ©ņ£äņ▓┤ņĀüļŗ╣ ļ¼╝ņØś ņ¢æņØĆ ŽüŽł=ŽülŽłŽĢSl+ŽügŽłŽĢ(1ŌłÆSl)ņØ┤ļ®░ ņ¦łļ¤ē ĒØÉļ”ä jŽł=ŽüŽł+ŽülŽłql+ŽügŽłqgņØ┤ļŗż. ĻĘĖļ”¼Ļ│Ā SlļŖö Ļ│ĄĻĘ╣(void)ņŚÉņä£ ņĢĪņ▓┤(liquid)ņØś ĒżĒÖöļÅäļź╝ ļéśĒāĆļé┤ļ®░, qlņÖĆ qgļŖö ņĢĪņ▓┤ ņāüĒā£ņÖĆ ĻĖ░ņ▓┤ ņāüĒā£ņØś ļŗ©ņ£äļ®┤ņĀüļŗ╣ ņ£Āļ¤ē(flow rate)ņØä ļéśĒāĆļéĖļŗż.
ņĀ£ņŗ£ļÉ£ ņāüĒśĖ ņØśņĪ┤ņĀü ņ¦Ćļ░░ļ░®ņĀĢņŗØļōżņŚÉ Galerkin ņłśņŗØĒÖöļź╝ ņĀüņÜ®ĒĢśĻ│Ā, ļ░®ņĀĢņŗØļōżņŚÉ ņé¼ļŗżļ”¼Ļ╝┤ ļ▓Ģņ╣ÖņØś ņŗ£Ļ░äņĀüļČä(Ōł½t(m)t(m+1)PdtŌēł╬öt[P(n)+╬Ė╬öP+╬ĖdP])Ļ│╝ NewtonņØś ļ░śļ│ĄĻ│╝ņĀĢņØä ļÅäņ×ģĒĢśņśĆļŗż. ņłśļ”¼ĒĢÖņĀü ĻĄ¼ņä▒ļ¬©ļŹĖļōżĻ│╝ ņŚ░Ļ│äĒĢśņŚ¼, ļŗżĻ│Ąņ¦ł ņ×¼ļŻīņŚÉņä£ ļŗżņāü ĒØÉļ”äņØś ņŚ░Ļ┤ĆļÉ£ ĒśäņāüņŚÉ ļīĆĒĢ£ ņłśņ╣śĒĢ┤ņäØņØä ņ£äĒĢśņŚ¼ Ļ░£ļ░£ļÉ£ Geo-COUS (Geo-COUpled Simulator) ņ£ĀĒĢ£ņÜöņåī ĒöäļĪ£ĻĘĖļשĻ│╝ Ļ▓░ĒĢ®ĒĢśņśĆļŗż.
3. ņ¦ĆĒæ£ļ®┤ ņ£ĀņČ£Ļ│╝ ņ¦Ćņżæ ņ╣©Ēł¼ ĒĢ┤ņäØ
Ļ░ĢņÜ░ņŚÉ ņØśĒĢ£ ņ¦ĆĒæ£ļ®┤ ņ£ĀņČ£Ļ│╝ ņ¦Ćņżæ ņ╣©Ēł¼ļŖö ņāüĒśĖ ņŚ░Ļ┤ĆļÉ£ Ēśäņāüņ£╝ļĪ£ ļÅÖņŗ£ņŚÉ Ļ│ĀļĀżĒĢśņŚ¼ ĒĢ┤ņäØņØä ņłśĒ¢ēĒĢśņŚ¼ņĢ╝ ĒĢ£ļŗż. Ļ░£ļ░£ļÉ£ ĒĢ┤ņäØ ļ¬©ļŹĖņØä ņØ┤ņÜ®ĒĢśņŚ¼ 1ņ░©ņøÉ ņĪ░Ļ▒┤ņŚÉņä£ ņ¦Ćņżæ ņ╣©Ēł¼(infiltration)ņÖĆ ņ¦ĆĒæ£ļ®┤ Ļ│Āņ×ä(ponding)ņŚÉ ļīĆĒĢ£ ņłśņ╣śĒĢ┤ņäØņØä ņłśĒ¢ēĒĢśņśĆļŗż. ļśÉĒĢ£, ļČłĒżĒÖö ņé¼ļ®┤ņŚÉņä£ Ļ░ĢņÜ░ņŚÉ ņØśĒĢ£ ņ¦ĆĒæ£ļ®┤ ņ£ĀņČ£Ļ│╝ ņ¦Ćļ░ś ņ╣©Ēł¼ņŚÉ ļīĆĒĢśņŚ¼ ļģ╝ņØśĒĢśņśĆļŗż. ņłśņ╣śĒĢ┤ņäØņØĆ 4ņĀłņĀÉņØś Ļ░äĻĘ╣ņłśņĢĢ ņ×Éņ£ĀļÅäļź╝ Ļ░¢ļŖö 2ņ░©ņøÉ ņ£ĀĒĢ£ņÜöņåīļź╝ ņé¼ņÜ®ĒĢśņśĆļŗż.
3.1 1ņ░©ņøÉ Ļ░ĢņÜ░ ņ╣©Ēł¼ ĒĢ┤ņäØ
Ļ░ĢņÜ░ņØś ņ¦Ćļ░ś ņ╣©Ēł¼ņÖĆ ņ¦ĆĒæ£ļ®┤ Ļ│Āņ×ä ĒśäņāüņŚÉ ĻĖ░ņĪ┤ņØś ņŚ░ĻĄ¼ļŖö ļīĆļČĆļČä Horton ļ¬©ļŹĖ, Philip ļ¬©ļŹĖ, Green-Ampt ļ¬©ļŹĖ ļō▒Ļ│╝ Ļ░ÖņØĆ Ļ▓ĮĒŚśņĀüņØĖ ļ░®ļ▓ĢņØä ņØ┤ņÜ®ĒĢśĻ│Ā ņ׳ļŗż. ĒĢśņ¦Ćļ¦ī, ļ¬©ļŹĖņŗØ ļōżņŚÉ ņé¼ņÜ®ļÉśļŖö Ļ│äņłśļōżņØĆ ņ¦Ćļ░śņØś ļČłĒżĒÖö/ĒżĒÖö ņłśļ”¼ĒĢÖņĀü ļ¼╝ņä▒ņ╣śņØś ņŚ░Ļ┤Ćņä▒ņØ┤ ļ¦żņÜ░ ļČĆņĪ▒ĒĢśļ®░, Ļ▓ĮĒŚśņĀüņØĖ ļ░®ļ▓ĢņØ┤ļéś ņŗżņĀ£ ņ╣©Ēł¼ ņŗżĒŚśņØä ĒåĄĒĢśņŚ¼ ĒÅēĻ░ĆĒĢśĻ│Ā ņ׳ļŗż. Ļ▓ĮĒŚśņĀü ļ¬©ļŹĖļōżņØä ļīĆņŗĀĒĢśņŚ¼, Ļ░£ļ░£ļÉ£ ņ¦ĆĒæ£ļ®┤ ņ£ĀņČ£Ļ│╝ ņŚ░Ļ│äļÉ£ ņ¦Ćņżæ ņ╣©Ēł¼ ļ¬©ļŹĖņØä ņØ┤ņÜ®ĒĢśņŚ¼ ņ¦Ćļ░śņØś ņłśļ”¼ĒĢÖņĀü ļ¼╝ņä▒Ļ│╝ ņ┤łĻĖ░ ņ¦Ćņżæ Ļ░äĻĘ╣ņłśņĢĢņ£╝ļĪ£ļČĆĒä░ ņŗ£Ļ░äĻ▓ĮĻ│╝ņŚÉ ļö░ļźĖ Ļ░ĢņÜ░ ņ¦Ćņżæ ņ╣©Ēł¼ļ¤ēĻ│╝ ņ¦ĆĒæ£ļ®┤ Ļ│Āņ×äņ¢æņØä ĒÅēĻ░ĆĒĢśĻ│Āņ×É ĒĢ£ļŗż. ņłśņ╣śĒĢ┤ņäØņŚÉ ņé¼ņÜ®ļÉ£ ņ¦Ćļ░śņØś ņłśļ”¼ĒĢÖņĀü ļ¼╝ņä▒ņ╣śļŖö ņÜĖņé░ņ¦ĆņŚŁ ĒÖöĻ░ĢĒÆŹĒÖöĒåĀ ņ¦Ćļ░śņØś ļ¼╝ņä▒ņ£╝ļĪ£
Table 1ņŚÉ ņĀĢļ”¼ĒĢśņśĆļŗż(
Kim and Shin, 2016). ņłśņ╣śĒĢ┤ņäØņØĆ ņ¦ĆĒæ£ļ®┤ņ£╝ļĪ£ļČĆĒä░ -10 m Ļ╣ŖņØ┤Ļ╣īņ¦Ć ņłśĒ¢ēĒĢśņśĆņ£╝ļ®░, 2,002ņØś ņĀłņĀÉņØä ņØ┤ņÜ®ĒĢśņŚ¼ 1,000ņØś ņŚ░ņåŹņ▓┤ ņ£ĀĒĢ£ņÜöņåīņÖĆ 1Ļ░£ņØś ņ¦ĆĒæ£ļ®┤ ņ£ĀņČ£ ņ£ĀĒĢ£ņÜöņåīļź╝ ņé¼ņÜ®ĒĢśņśĆļŗż.
Table┬Ā1
Hydraulic Soil Properties in Numerical Simulations
|
Model |
Soil parameters |
|
Water retention curve: Se=[1+(Pca)b]ŌłÆc
|
a=5.76 kPa, b=1.285, c=0.222 |
|
Intrinsic hydraulic conductivity:kl [m/s] |
1.0├Ś10ŌłÆ5
|
|
Relative hydraulic conductivity: krl=(se)(1ŌłÆ(1ŌłÆSe1/╬╗)╬╗)2
|
╬╗=0.22 |
Fig. 1ņØĆ ņ¦ĆĒæ£ļ®┤ņØś Ļ░äĻĘ╣ņłśņĢĢņØ┤ -50kPaņØ┤Ļ│Ā Ļ╣ŖņØ┤ņŚÉ ļö░ļźĖ ņĀĢņłśņĢĢ ļČäĒżļź╝ Ļ░¢ļŖö ņ¦Ćļ░śņŚÉ ļīĆĒĢśņŚ¼ Ļ░ĢņÜ░Ļ░ĢļÅäņŚÉ ļö░ļźĖ ņ¦Ćņżæ ņ╣©Ēł¼ļ¤ēĻ│╝ ņ¦ĆĒæ£ļ®┤ Ļ│Āņ×äļ¤ēņŚÉ ļīĆĒĢ£ ņłśņ╣śĒĢ┤ņäØ Ļ▓░Ļ│╝ļź╝ ļ│┤ņŚ¼ņŻ╝Ļ│Ā ņ׳ļŗż. ņ¦Ćļ░śņØś ĒżĒÖöĒł¼ņłśĻ│äņłś (ksat=36mm/hr)ļ│┤ļŗż ņ×æņØĆ Ļ░ĢņÜ░Ļ░ĢļÅäņŚÉņä£ļŖö ņ¦ĆĒæ£ļ®┤ņØś Ļ│Āņ×äĒśäņāüņØ┤ ļ░£ņāØĒĢśņ¦Ć ņĢŖĻ│Ā, ņĀäĻ░ĢņÜ░ļ¤ēņØĆ ĒĢśļČĆ ņ¦Ćļ░śņ£╝ļĪ£ ņ╣©Ēł¼ĒĢśņśĆļŗż.
Fig.┬Ā1
Surface Ponding and Infiltration During Rainfall. a) Rain-surface ponding-infiltration at rainfall intensity I=30 mm/hr, b) Rain-surface ponding-infiltration at rainfall intensity I=90 mm/hr, c) Time history of infiltration rate at various rainfall intensity.

ĒĢśņ¦Ćļ¦ī, ĒżĒÖöĒł¼ņłśĻ│äņłśņŚÉ ņĀæĻĘ╝ĒĢśļ®┤ņä£ ņ¦ĆĒæ£ļ®┤ Ļ│Āņ×äĒśäņāüņØ┤ ļ░£ņāØĒĢśĻĖ░ ņŗ£ņ×æĒĢśĻ│Ā (
Fig. 1(a)), ņ¦Ćļ░śņØś ksat ļ│┤ļŗż Ēü░ Ļ░ĢņÜ░Ļ░ĢļÅäņŚÉņä£ Ļ░ĢņÜ░ ņ┤łĻĖ░ļČĆĒä░ ņ¦ĆĒæ£ļ®┤ņØś ņłśņ£äĻ░Ć ņāüņŖ╣ĒĢ©ņØä ņĢī ņłś ņ׳ļŗż (
Fig. 1(b)).
Fig. 1(c)ļŖö ļŗżņ¢æĒĢ£ Ļ░ĢņÜ░ņĪ░Ļ▒┤ņŚÉ ļīĆĒĢśņŚ¼ ņŗ£Ļ░äĻ▓ĮĻ│╝ ņŚÉ ļö░ļźĖ ņ¦Ćņżæ ņ╣©Ēł¼ņ£©ņØä ļéśĒāĆļé┤Ļ│Ā ņ׳ļŗż. ļ¬©ļōĀ Ļ░ĢņÜ░Ļ░ĢļÅä ņĪ░Ļ▒┤ņŚÉņä£ Ļ░ĢņÜ░ ņ┤łĻĖ░ņŚÉ ņ¦Ćņżæ ņ╣©Ēł¼ņ£©ņØĆ Ļ░ĢņÜ░ Ļ░ĢļÅäņÖĆ ļÅÖņØ╝ĒĢśĻ▓ī ļéśĒāĆļéśĻ│Ā ņ׳ļŗż.
ņ¦Ćļ░śņØś ksat ļ│┤ļŗż ņ×æņØĆ Ļ░ĢņÜ░Ļ░ĢļÅä(20 mm/hr)ļŖö ņ¦ĆĒæ£ļ®┤ņŚÉ Ļ│Āņ×äĒśäņāüņØ┤ ņŚåņØ┤ ņĀäļČĆ ņ¦Ćņżæņ£╝ļĪ£ ņ╣©Ēł¼ĒĢ©ņØä ņĢī ņłś ņ׳ļŗż. ĒĢśņ¦Ćļ¦ī, Ēü░ Ļ░ĢņÜ░Ļ░ĢļÅä(90 mm/hr)ņŚÉņä£ļŖö Ļ░ĢņÜ░Ļ░ĢļÅäņÖĆ ļÅÖņØ╝ĒĢ£ ņ┤łĻĖ░ ņ╣©Ēł¼ņ£©ņŚÉņä£ ņŗ£Ļ░ä Ļ▓ĮĻ│╝ņŚÉ ļö░ļØ╝ ĻĖēĻ▓®ĒĢśĻ▓ī Ļ░ÉņåīĒĢśņśĆļŗż.
Fig. 1(c)ļŖö ņ¦Ćņżæ ņ╣©Ēł¼ņ£©ņØ┤ ņĄ£ņåīĻ░ÆņŚÉ ļÅäļŗ¼ĒĢ£ ĒøäņŚÉ ņØ╝ņĀĢĒĢ£ Ļ░ÆņŚÉ ņłśļĀ┤ĒĢ©ņØä ļ│┤ņŚ¼ņŻ╝Ļ│Ā ņ׳ļŗż. ĻĖ░ņĪ┤ņØś Ļ▓ĮĒŚśņŗØĻ│╝ ļŗ¼ļ”¼, ņ¦Ćņżæ ņ╣©Ēł¼ņ£©ņØ┤ ņØ╝ņĀĢĒĢ£ Ļ░ÆņØ┤ ļÅäļŗ¼ĒĢśļŖö ņŗ£ņĀÉņØĆ ņ¦ĆĒæ£ļ®┤ Ļ│Āņ×äĒśäņāüņØ┤ ļ░£ņāØĒĢśļŖö ņŗ£ņĀÉļ│┤ļŗż ļŖ”ļŗżļŖö Ļ▓āņØä ņĢīņłś ņ׳ļŗż. ĻĘĖļ”¼Ļ│Ā, Ļ░ĢņÜ░Ļ░ĢļÅäĻ░Ć ņ”ØĻ░ĆĒĢĀņłśļĪØ ņ¦ĆĒæ£ļ®┤ Ļ│Āņ×äĒśäņāüĻ│╝ ņ╣©Ēł¼ņ£©ņØ┤ ņØ╝ņĀĢĒĢśļŖö ņłśļĀ┤ĒĢśļŖö ņŗ£ņĀÉņØ┤ ļ╣©ļØ╝ņ¦ÉņØä ņĢī ņłś ņ׳ļŗż. ĻĖ░ņĪ┤ņØś Ļ▓ĮĒŚśņŗØņØĆ ņłśļĀ┤ļÉ£ ņ¦Ćņżæ ņ╣©Ēł¼ņ£©ņØ┤ Ļ░ĢņÜ░Ļ░ĢļÅäņÖĆ ļ¼┤Ļ┤ĆĒĢśņ¦Ćļ¦ī, Ļ░ĢņÜ░Ļ░ĢļÅäĻ░Ć ņ”ØĻ░ĆĒĢĀņłśļĪØ ņłśļĀ┤ļÉ£ ņ¦Ćņżæ ņ╣©Ēł¼ņ£©ņØ┤ ņ”ØĻ░ĆĒĢśļŖö Ļ▓āņØĆ ņ¦ĆĒæ£ļ®┤ Ļ│Āņ×äņŚÉ ņØśĒĢ£ ņłśņĢĢĻ│╝ ņ╣©ņ£żņäĀ ņØ┤ļÅÖņŚÉ ņØśĒĢ£ Ļ▓āņØ┤ļŗż(
Fig. 1(c)).
3.2 ĒåĀņé¼ņé¼ļ®┤ņŚÉ ļīĆĒĢ£ Ļ░ĢņÜ░ ĒĢ┤ņäØ
ĻĖ░ņĪ┤ņØś Ļ░ĢņÜ░ņŚÉ ņØśĒĢ£ ļČłĒżĒÖö ņé¼ļ®┤ņØś ņłśļ”¼ĒĢ┤ņäØņŚÉņä£ ņ¦Ćņżæ ņ╣©Ēł¼ļ¤ēņØä ņ×äņØśļĪ£ Ļ░ĆņĀĢĒĢśĻ▒░ļéś Ļ▓ĮĒŚśņĀüņØĖ ļ░®ļ▓Ģņ£╝ļĪ£ Ļ▓░ņĀĢĒĢśņśĆļŗż(
Moon et al., 2008;
Hwang, 2015). ĒĢśņ¦Ćļ¦ī, ņÜ░ĻĖ░ņŚÉ ļ░£ņāØĒĢśļŖö ņé¼ļ®┤ņØś ņĢłņĀĢņä▒ ļ¼ĖņĀ£ļŖö ņé¼ļ®┤ļé┤ļČĆļĪ£ņØś Ļ░ĢņÜ░ņ╣©Ēł¼ ļ┐Éļ¦ī ņĢäļŗłļØ╝, ņ¦ĆĒæ£ļ®┤ ņ£ĀņČ£ņŚÉ ņØśĒĢ£ ņé¼ļ®┤ ĒĢśļČĆņØś Ļ│Āņ×ä ĒśäņāüņŚÉ ņśüĒ¢źņØä ļ░øĻ▓ī ļÉ£ļŗż. 5m ļåÆņØ┤ņØś ļČłĒżĒÖö ņé¼ļ®┤ņŚÉ Ļ░ĢņÜ░ļź╝ ņ¦ĆĒæ£ļ®┤ņŚÉ ņ¦üņĀæ ņ£Āļ¤ēņ£╝ļĪ£ ņ×¼ĒĢśĒĢśļŖö Ļ▓ĮņÜ░(Flux BC)ņÖĆ Ļ░£ļ░£ļÉ£ ņ¦ĆĒæ£ļ®┤ ņ£ĀņČ£Ļ│╝ ņŚ░Ļ│äļÉ£ ņ¦Ćņżæ ņ╣©Ēł¼ ļ¬©ļŹĖ(Runoff BC)ņØä ņØ┤ņÜ®ĒĢ£ ņłśņ╣ś ĒĢ┤ņäØ Ļ▓░Ļ│╝ļź╝ ļ╣äĻĄÉ ļČäņäØĒĢśņśĆļŗż. ņ¦ĆĒĢśņłśņ£äļŖö ņé¼ļ®┤ĒĢśļČĆņŚÉņä£ -5 mņŚÉ ņ£äņ╣śņŚÉ 2%ņØś Ļ▓Įņé¼ļź╝ Ļ░¢ļŖö Ļ▓āņ£╝ļĪ£ Ļ░ĆņĀĢĒĢśņśĆņ£╝ļ®░, 27,421ņØś ņĀłņĀÉņØä ņØ┤ņÜ®ĒĢśņŚ¼ 9,000ņØś ņŚ░ņåŹņ▓┤ ņ£ĀĒĢ£ņÜöņåīņÖĆ 150Ļ░£ņØś ņ¦ĆĒæ£ļ®┤ ņ£ĀņČ£ ņ£ĀĒĢ£ņÜöņåīļź╝ ņé¼ņÜ®ĒĢśņśĆļŗż. ņé¼ļ®┤ ĒĢśļČĆ ņ¦Ćļ®┤ņØś Ļ▓Įņé¼ļŖö ņé¼ļ®┤ ĻĖ░ņŖŁ(foot of slope) ļ░®Ē¢źņ£╝ļĪ£ 2%ņØ┤ļ®░, Ļ░ĢņÜ░ļŖö ņ┤łĻĖ░ 1ņŗ£Ļ░ä ļÅÖņĢł ņ¦ĆņåŹĒĢśņśĆļŗż.
Fig. 2ņŚÉņä£ ŌĆ£Flux BCŌĆØļŖö ņ¦ĆĒæ£ļ®┤ņŚÉ Ļ░ĢņÜ░Ļ░ĢļÅäļź╝ ņ£Āļ¤ēņ£╝ļĪ£ ņ¦üņĀæ ņĀüņÜ®ņŗ£Ēé© ņłśņ╣śĻĖ░ļ▓ĢņŚÉ ļīĆĒĢ£ ĒĢ┤ņäØ Ļ▓░Ļ│╝ņØ┤ļŗż. Ļ░Ģņ×¼ņĀüņØĖ ņ£Āļ¤ēņŻ╝ņ×ģņ£╝ļĪ£ ņØĖĒĢśņŚ¼ Ļ░ĢņÜ░ņŗ£ ņ¦ĆĒæ£ļ®┤ņŚÉ ļåÆņØĆ Ļ░äĻĘ╣ņłśņĢĢņØä Ļ░¢ļŖö ĻĘĀļō▒ĒĢ£ Ļ╣ŖņØ┤ņØś ĒżĒÖöļīĆņĖĄņØ┤ ĒśĢņä▒ļÉśļ®░, Ļ░ĢņÜ░ ņóģļŻī Ēøä ļåÆņØĆ Ļ░äĻĘ╣ņłśņĢĢņØ┤ ņŻ╝ņ£äņØś ņØīņØś Ļ░äĻĘ╣ņłśņĢĢņ£╝ļĪ£ ĒÖĢņé░ļÉśļ®┤ņä£ ĻĘĀļō▒ĒĢ£ ĒżĒÖöļīĆņĖĄņØ┤ ĒĢśļČĆļĪ£ ņ¦äĒ¢ēĒĢ©ņØä ņĢī ņłś ņ׳ļŗż.
Fig.┬Ā2
Pore Water Distribution of the Slope from Rainfall Pattern with Intensity 90mm/hr and Duration 1 Hour
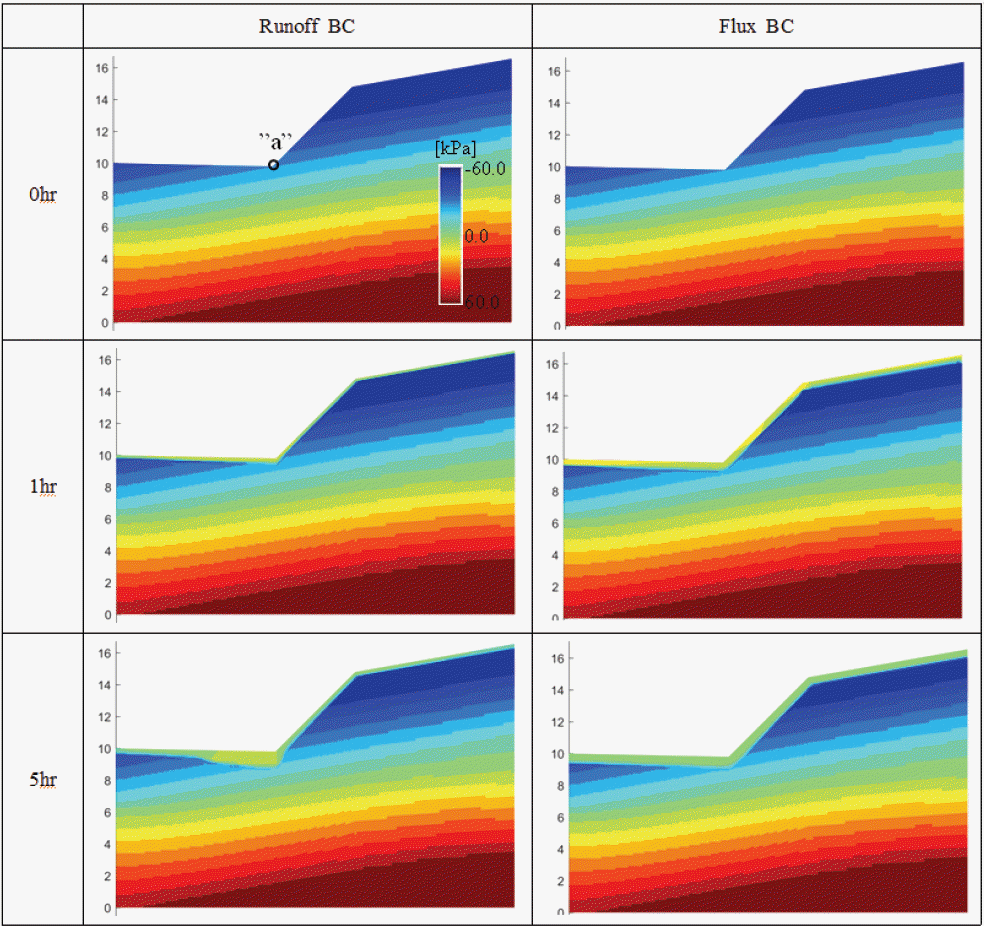
ŌĆ£Runoff BCŌĆØļŖö Ļ░£ļ░£ļÉ£ ņ¦ĆĒæ£ļ®┤ņØś ņ£ĀņČ£Ļ│╝ ņŚ░Ļ│äļÉ£ ņ¦Ćņżæ ņ╣©Ēł¼ĒĢ┤ņäØ ļ░®ļ▓ĢņŚÉ ņØśĒĢ£ ĒĢ┤ņäØ Ļ▓░Ļ│╝ļź╝ ļéśĒāĆļé┤Ļ│Ā ņ׳ļŗż. Ļ░ĢņÜ░ņŗ£ ņ¦ĆĒæ£ļ®┤ ņ£ĀņČ£ļĪ£ ņØĖĒĢśņŚ¼ ņé¼ļ®┤ļé┤ļČĆņŚÉ ņ¢ćņØĆ ĒżĒÖöļīĆņĖĄņØ┤ ĒśĢņä▒ļÉśļ®░, ņ¦ĆĒśĢņĪ░Ļ▒┤ņŚÉ ņØśĒĢśņŚ¼ ņé¼ļ®┤ņØś ĻĖ░ņŖŁņŚÉ ņ£ĀņČ£ņłśĻ░Ć Ļ│ĀņØ┤ĻĖ░ ņŗ£ņ×æĒĢ©ņØä ņĢī ņłś ņ׳ļŗż. ĻĘĖļ”¼Ļ│Ā Ļ░ĢņÜ░ ņóģļŻī Ēøä ņé¼ļ®┤ ļ╣äĒāłļ®┤ņŚÉļŖö ņāüļīĆņĀüņ£╝ļĪ£ ņ¢ćņØĆ ĒżĒÖöļīĆņĖĄņØ┤ ĒśĢņä▒ļÉśņ¦Ćļ¦ī, ņé¼ļ®┤ ĻĖ░ņŖŁņŚÉļŖö ļ¬©ņŚ¼ļōĀ ņ£ĀņČ£ņłśņŚÉ ņØśĒĢśņŚ¼ ĒżĒÖöļīĆņĖĄņØ┤ Ļ╣ŖĻ│Ā ļäōĻ▓ī ĒśĢņä▒ļÉśņ¢┤ ņ׳ņØīņØä ņĢī ņłś ņ׳ļŗż.
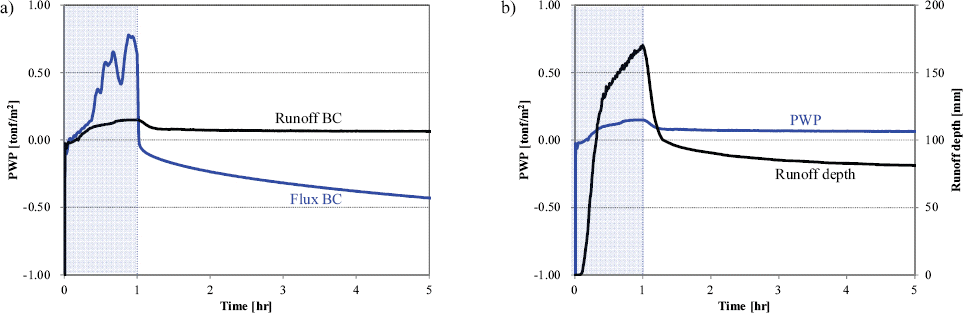
Fig. 3(a)ļŖö Flux BCĻ│╝ Runoff BC ĒĢ┤ņäØņŚÉ ņØśĒĢ£ ņé¼ļ®┤ ĻĖ░ņŖŁ (
Fig. 2ņØś ŌĆ£aŌĆØ)ņŚÉņä£ ņŗ£Ļ░äĻ▓ĮĻ│╝ņŚÉ ļö░ļźĖ Ļ░äĻĘ╣ņłśņĢĢņØś ļ│ĆĒÖöļź╝ ļéśĒāĆļé┤Ļ│Ā ņ׳ļŗż. Flux BC ņłśņ╣śĒĢ┤ņäØļ▓ĢņŚÉņä£ ņ¦Ćļ░śņØś ĒżĒÖöĒł¼ņłśĻ│äņłśņŚÉ ĻĘ╝ņĀæĒĢśļŖö Ļ░ĢņÜ░Ļ░ĢļÅäļŖö ņ£Āļ¤ēņĪ░Ļ▒┤ņØä ļ¦īņĪ▒ņŗ£ĒéżĻĖ░ ņ£äĒĢśņŚ¼ ņØ╝ņŗ£ņĀüņ£╝ļĪ£ Ļ░ĆņāüņØś ļåÆņØĆ Ļ░äĻĘ╣ņłśņĢĢņØä ņ£Āļ░£ĒĢśĻ│Ā, ĒĢ┤ņäØ Ļ▓░Ļ│╝ņØś ļČłņĢłņĀĢĒĢ£ ņÜöļÅÖ(oscillation)ņØä ņ£Āļ░£ĒĢśĻ▓ī ļÉ£ļŗż. ļśÉĒĢ£ ņ£Āļ¤ēņØś ņŻ╝ņ×ģņØ┤ ņÖäļŻīļÉ£ Ēøä, Ļ░äĻĘ╣ņłśņĢĢņØ┤ ĻĖēĻ▓®ĒĢśĻ▓ī Ļ░ÉņåīĒĢśļŖö ĒśäņāüņØä ļ│┤ņØ┤Ļ▓ī ļÉ£ļŗż. ņØ┤ļ¤¼ĒĢ£ Ļ░ĆņāüņØś ņłśņ╣śņĀüņØĖ ļČłņĢłņĀĢņä▒ņØä ņĄ£ņåīĒÖöĒĢśĻĖ░ ņ£äĒĢśņŚ¼ ņłśņ╣śĒĢ┤ņäØ Ļ▓░Ļ│╝ņŚÉ ļīĆĒĢ£ ņØĖņ£äņĀüņØĖ ņĢłņĀĢĒÖöĻ░Ć ĒĢäņÜöĒĢśĻ▓ī ļÉ£ļŗż (
Karthikeyan et al., 2001). ļ░śļ®┤ Runoff BC ņłśņ╣śĒĢ┤ņäØļ▓ĢņŚÉņä£ļŖö ļ╣äĒāłņé¼ļ®┤ņØä ļö░ļØ╝ ņ£ĀņČ£ļÉ£ Ļ░ĢņÜ░Ļ░Ć ņé¼ļ®┤ ĻĖ░ņŖŁņŚÉ ņ¦æņłśļÉśļ®┤ņä£ ņ¦ĆĒæ£ļ®┤ Ļ░äĻĘ╣ņłśņĢĢņØ┤ Ļ░ĢņÜ░ļ¤ēļ│┤ļŗż Ēü¼Ļ▓ī ļéśĒāĆļé©ņØä ņĢī ņłś ņ׳ļŗż. Ļ░ĢņÜ░ ņóģļŻī Ēøä, ņ¦ĆĒæ£ļ®┤ņØś Ļ░äĻĘ╣ņłśņĢĢņØĆ ĻĖēĻ▓®Ē׳ Ļ░ÉņåīĒĢ£ Ēøä ņØīņØś Ļ░Æņ£╝ļĪ£ ņłśļĀ┤ĒĢśĻ▓ī ļÉ£ļŗż. ņ£ĀņČ£ņłśņŚÉ ņØśĒĢ£ ņ¦ĆĒæ£ļ®┤ ņłśņ£äļŖö Ļ░ĢņÜ░ ņ¦ĆņåŹņŗ£Ļ░ä ļÅÖņĢł ņ”ØĻ░ĆĒĢ£ Ēøä, Ļ░ĢņÜ░ņóģļŻī Ēøä ņÖäļ¦īĒĢśĻ▓ī Ļ░ÉņåīĒĢ£ļŗż. ņ¦ĆĒæ£ļ®┤ņØś ņØīņØś Ļ░äĻĘ╣ņłśņĢĢĻ│╝ ņ¦ĆĒæ£ļ®┤ ņ¢æņØś ņłśņ£äļŖö Ļ░ĢņÜ░ ņóģļŻī Ēøä ņ¦ĆĒæ£ņłśĻ░Ć ņ¦ĆņåŹņĀüņ£╝ļĪ£ ņ¦Ćņżæņ£╝ļĪ£ ņ╣©Ēł¼ļÉśĻ│Ā ņ׳ņØīņØä ļéśĒāĆļé┤Ļ│Ā ņ׳ļŗż(
Fig. 3(b)).
Fig.┬Ā3
a) Pore Water Pressure Comparison at Slope Foot ŌĆ£aŌĆØ from direct flux injection onto the soil surface (ŌĆ£Flux BCŌĆØ) and developed surface runoff-subsurface infiltration model (ŌĆ£Runoff BCŌĆØ), b) Evolution of pore water pressure and runoff depth at slope foot ŌĆ£aŌĆØ using surface runoff-subsurface infiltration model (ŌĆ£Runoff BCŌĆØ).
4. Ļ▓░ļĪĀ
Ļ░ĢņÜ░ņŚÉ ņØśĒĢ£ ņé¼ļ®┤ņØś ņłśļ”¼ĒĢÖņĀü ĒĢ┤ņäØņŚÉņä£ ņ¦ĆĒæ£ļ®┤ ņ£ĀņČ£Ļ│╝ ņ¦Ćņżæ ņ╣©Ēł¼ļŖö ņāüĒśĖ ņŚ░Ļ┤ĆļÉ£ ĻĘĖļ”¼Ļ│Ā ļ¦żņÜ░ ņżæņÜöĒĢ£ ņłśļ”¼ĒĢÖņĀü ĒśäņāüņØ┤ļŗż. ĒĢśņ¦Ćļ¦ī, ĻĖ░ņĪ┤ņØś ļīĆļČĆļČäņØś ņŚ░ĻĄ¼ņŚÉņä£ ņ£ĀņČ£Ļ│╝ ņ╣©Ēł¼ņØś ņŚ░Ļ│äļÉ£ ĒĢ┤ņäØņØä ņłśĒ¢ēĒĢśņ¦Ć ņĢŖĻ│Ā, ņ¦ĆĒæ£ļ®┤ ņ£ĀņČ£ņØä ļ¼┤ņŗ£ĒĢśĻ│Ā ņØ╝ņĀĢļ¤ēņØś ņ£Āļ¤ēņØä ņ¦üņĀæ ņ¦ĆĒæ£ļ®┤ņŚÉ ņŻ╝ņ×ģĒĢśļŖö ĒśĢĒā£ļź╝ ņłśņ╣śĒĢ┤ņäØņØä ņłśĒ¢ēĒĢśĻ│Ā ņ׳ļŗż. ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö ņ¦ĆĒæ£ļ®┤ ņ£ĀņČ£ņŚÉ ļīĆĒĢ£ ņ¦Ćļ░░ļ░®ņĀĢņŗØņØä ņĀ£ņŗ£ĒĢśĻ│Ā ĒĢ┤ņØś ņĢłņĀĢņä▒ ĒÖĢļ│┤ĒĢśĻĖ░ ņ£äĒĢ£ ņłśņŗØĒÖö ĻĖ░ļ▓ĢņØä ņĀ£ņŗ£ĒĢśņśĆļŗż. ļśÉĒĢ£ ņ¦Ćņżæ ņ╣©Ēł¼ņÖĆ ņŚ░Ļ│äĒĢśĻĖ░ ņ£äĒĢśņŚ¼ ļČłĒżĒÖö ņ¦Ćļ░śņØś ņłśļ”¼ĒĢÖņĀü ĒśäņāüņŚÉ ļīĆĒĢ£ ņłśņĀĢļÉ£ ņ¦Ćļ░░ļ░®ņĀĢņŗØņØä ņĀ£ņŗ£ĒĢśņśĆļŗż.
(1) Ļ░£ļ░£ļÉ£ ņ¦ĆĒæ£ļ®┤ ņ£ĀņČ£Ļ│╝ ņŚ░Ļ│äļÉ£ ņ¦Ćņżæ ņ╣©Ēł¼ ļ¬©ļŹĖņØä ņØ┤ņÜ®ĒĢśņŚ¼ 1ņ░©ņøÉ Ļ░ĢņÜ░ ņ╣©Ēł¼ ĒĢ┤ņäØņØä ņłśĒ¢ēĒĢśņśĆļŗż. ļŗżņ¢æĒĢ£ Ļ░ĢņÜ░Ļ░ĢļÅäņŚÉ ļīĆĒĢ£ ņłśņ╣ś ĒĢ┤ņäØ Ļ▓░Ļ│╝ļŖö ĻĖ░ņĪ┤ņØś Ļ▓ĮĒŚśņŗØĻ│╝ Ļ░ÖņØĆ Ļ░ĢņÜ░ņŚÉ ņØśĒĢ£ ņ┤łĻĖ░ ņ╣©Ēł¼ļ¤ēņØś Ļ░ÉņåīņÖĆ ņłśļĀ┤ļÉ£ ĒżĒÖö ņ╣©Ēł¼ļ¤ēņØä ļ│┤ņŚ¼ņŻ╝ņŚłļŗż. ĒĢśņ¦Ćļ¦ī, ļŗ©ņł£ĒÖöļÉ£ ĻĖ░ņĪ┤ Ļ▓ĮĒŚśņŗØĻ│╝ ļŗ¼ļ”¼, Ļ░£ļ░£ļÉ£ ļ¬©ļŹĖņØĆ Ļ░ĢņÜ░ņĪ░Ļ▒┤ņŚÉ ļö░ļźĖ ņ¦ĆĒæ£ļ®┤ Ļ│Āņ×äĒśäņāüĻ│╝ ņ¦Ćņżæ ņ╣©Ēł¼ņ£©ņØś ļ│ĆĒÖöļź╝ ņ¦Ćļ░śņØś ņłśļ”¼ĒĢÖņĀü ļ¼╝ņä▒ņØä ņØ┤ņÜ®ĒĢśņŚ¼ ĒÜ©Ļ│╝ņĀüņ£╝ļĪ£ ļ¬©ļŹĖļ¦üĒĢĀ ņłś ņ׳ņŚłļŗż.
(2) ļČłĒżĒÖö ļ╣äĒāł ņé¼ļ®┤ņŚÉ ļīĆĒĢ£ Ļ░ĢņÜ░ņ×¼ĒĢś ņłśņ╣śĒĢ┤ņäØņŚÉņä£ ĻĖ░ņĪ┤ņØś ņ¦ĆĒæ£ļ®┤ņŚÉ ņ£Āļ¤ēņØä ņ¦üņĀæ ņ×¼ĒĢśĒĢśļŖö ĒĢ┤ņäØĻĖ░ļ▓ĢņØĆ ņ┤łĻĖ░ņØś ņ¦ĆĒæ£ļ®┤ņŚÉ Ļ│╝ņןļÉ£ ĻĘĖļ”¼Ļ│Ā ļČłņĢłņĀĢĒĢ£ Ļ░äĻĘ╣ņłśņĢĢņØä ļ░£ņāØņŗ£ņ╝░ļŗż. ĒĢśņ¦Ćļ¦ī, ņ¦ĆĒæ£ļ®┤ ņ£ĀņČ£Ļ│╝ ņŚ░Ļ│äļÉ£ ņ¦Ćņżæ ņ╣©Ēł¼ ļ¬©ļŹĖņØĆ Ļ░ĢņÜ░ņŗ£ ņ¦ĆĒæ£ļ®┤ ņ£ĀņČ£ņŚÉ ņØśĒĢ£ ņ¦æņłś ĒśäņāüĻ│╝ ņ¦Ćņżæ ņ╣©Ēł¼ļź╝ ņŚ░Ļ│äĒĢśņŚ¼ ļ│┤ļŗż ĒśäņŗżņĀüņØĖ Ļ░äĻĘ╣ņłśņĢĢņØś ļ│ĆĒÖöļź╝ ļ│┤ņŚ¼ņŻ╝Ļ│Ā ņ׳ļŗż.
Ļ░Éņé¼ņØś ĻĖĆ
ļ│Ė ņŚ░ĻĄ¼ļŖö ĻĄŁĒåĀĻĄÉĒåĄļČĆ/ĻĄŁĒåĀĻĄÉĒåĄĻ│╝ĒĢÖĻĖ░ņłĀņ¦äĒØźņøÉ Ļ▒┤ņäż ĻĖ░ņłĀņŚ░ĻĄ¼ņé¼ņŚģ(13SCIPS04)ņØś ņŚ░ĻĄ¼ļ╣äņ¦ĆņøÉņŚÉ ņØśĒĢ┤ ņłśĒ¢ēļÉśņŚłņŖĄļŗłļŗż.
References
Hwang, Y.C (2015) Change of Slope Stability Due to Slope Inclination and Surface Conditions.
Journal of the Korean Geotechnical Society, Vol. 31, No. 2, pp. 5-11. 10.7843/kgs.2015.31.2.5.

Karthikeyan, M, Tan, T.S, and Phoon, K.K (2001) Numerical Oscillation in Seepage Analysis of Unsaturated Soils.
Can. Geotech. J, Vol. 38, No. 3, pp. 639-651. 10.1139/t01-018.

Kim, J, and Shin, H (2016) Slope Stability Assessment on a Landslide Risk Area in Ulsan during Rainfall.
Journal of the Korean Geotechnical Society, Vol. 32, No. 6, pp. 27-40. 10.7843/kgs.2016.32.6.27.

Kollet, S.J, and Maxwell, R.M (2006) Integrated Surface- groundwater Flow Modeling: A Free-surface Overland Flow Boundary Condition in a Parallel Groundwater Flow Model.
Adv. Water Resour, Vol. 29, No. 7, pp. 945-958. 10.1016/j.advwatres.2005.08.006.

Lee, J.S (2015).
Hydrology. 2nd Edition. Gumiseogwan.

Moon, Y.I, Lee, I.J, and Oh, T.S (2008) Estimation of Infiltration and Simulation of Seepage Behavior in Slope using the Rainfall Data in Seoul.
J. Korean Soc. Hazard Mitig, Vol. 8, No. 5, pp. 103-109.

Panday, S, and Huyakorn, P.S (2004) A Fully Coupled Physically-based Spatially-distributed Model for Evaluating Surface/Subsurface Flow.
Adv. Water Resour, Vol. 27, No. 4, pp. 361-382. 10.1016/j.advwatres.2004.02.016.

Phoon, K.K, Tan, T.S, and Chong, P.C (2007) Numerical Simulation of Richards Equation in Partially Saturated Porous Media: Under-relaxation and Mass Balance.
Geotech. Geol. Eng, Vol. 25, No. 5, pp. 525-541. 10.1007/s10706-007-9126-7.

Shin, H (2011) Formulation of Fully Coupled THM Behavior in Unsaturated Soil.
Journal of the Korean Geotechnical Society, Vol. 27, No. 3, pp. 75-83. 10.7843/kgs.2011.27.3.075.

Thomas, H.R, and Zhou, Z (1997) Minimum Time-Step Size for Diffusion Problem in FEM Analysis.
International Journal for Numerical Methods in Engineering, Vol. 40, No. 20, pp. 3865-3880. 10.1002/(SICI)1097-0207(19971030)40:20<3865::AID-NME246>3.0.CO;2-C.

Zienkiewicz, O.C, Taylor, R.L, and Nithiarasu, P (2005).
The Finite Element Method for Fluid Dynamics. 6th Edition. Butterworth-Heinemann.












