|
 |
- Search
| J. Korean Soc. Hazard Mitig. > Volume 18(2); 2018 > Article |
|
Abstract
The water distribution system is an important social infrastructure providing customers with stable and safe water supply. The fact, however, is that it is not free from various abnormal situations arising from internal / external factors. In case of a water supply failure due to an abnormal situation, the emergency interconnected operation between adjacent blocks in the system is one of the most effective countermeasures. To simulate these types of emergency operations, existing hydraulic analysis model which are based on infinite source assumption may result in unrealistic results such as negative pressure at demand nodes. Having more realistic simulation results from these situations, it is required to use an A-PDA model considering the reservoir volume and the inflow volume of the reservoir. With this consideration, the A-PDA model can simulate the condition of the limited amount of water supply. We apply the A-PDA model to the emergency interconnected operation between adjacent blocks in a city in Korea and find that more realistic results can obtained comparing with the results obtained from the PDA model which is based on the unlimited water supply.
요지
상수관망 시스템은 중요 사회기반시설로 안정적이고 안전한 공급을 추구하나, 내/외적인 요인들로부터 발생하는 각종 비정상상황으로부터 자유롭지 못하다. 비정상상황으로 인한 용수공급에 차질이 생길 시, 수계전환에 따른 비상급수는 매우 효율적인 대비책 중 하나로서 수리해석을 통해 공급능력 평가 및 관망의 설계 보완 방안을 제시할 수 있다. 하지만 기존의 수리해석 모형들은 무한수원의 가정을 적용하고 있는 바, 비상연계 수리해석 시 비현실적인 결과를 도출할 수 있다. 이에 배수지의 저류량과 유입량을 고려한 Advanced-Pressure Driven Analysis(A-PDA) 모형을 적용하여 A시의 수계전환 시나리오를 모의하였으며, 기존 PDA 모형의 결과와의 비교를 통하여 A-PDA 모형이 현실적인 결과를 도출하였음을 확인하였다.
환경부 상수도 통계자료에 따르면 2015년도 기준 국내의 급수인구는 5,200만 명을 넘어섰으며, 그 보급률은 98.8%에 달한다. 또한 국내 총 관로 연장은 197,535 km로 매년 증가하는 추세를 보인다. 이와 같은 상수관망 시스템은 중요 사회기반시설로 질적으로 안전하고 양적으로 충분한 물을 적절한 수압으로 수요자들에게 공급하는 것을 추구하고 있으나, 내/외적인 요인들부터 발생하는 각종 비정상상황으로부터 자유롭지 못하다. 상수관망 시스템에서의 문제발생 요인은 배수지의 오염 및 설비 문제, 화재 발생으로 인한 수요량의 급증, 관로공사로 인한 시스템의 비운영 등과 같이 매우 다양하며, 관망의 개량 사업 등의 사전 방지책에도 불구하고 공급관련 사고를 완전히 방지할 수 없다는 필연적인 문제점을 갖는다.
상수관망 시스템에 예기치 못한 문제가 발생하여 용수 공급에 차질이 생길 경우, 일부 구역에서의 단수피해를 야기하며 주민들의 삶의 질과 경제에 직접적인 영향을 끼친다. 다음과 같은 비정상상황에서 피해를 최소화하기 위해서는, 단수에 대한 사후 대책 대비가 필수적이다. 수계전환에 따른 비상급수는 가장 효율적인 대비책 중 하나로써, 수도법 제4조에 따른 수도정비기본계획의 수립에도 연계 운영의 필요성이 명시되어 있으며, Walski(1993)의 상수관망의 신뢰성 확보를 위한 실증적 연구에서도 비상연계 시스템 설계의 필요성이 언급되어 있다.
수계전환을 통한 비상연계는 상수관망 운영중단과 같은 비정상상황에서 단수가 발생한 배수블록으로부터 인접한 블록에서 비상관로를 통하여 수계를 전환함으로써 물 공급을 실시하는 것을 의미한다. 수리학적 해석을 통하여 비상연계 시의 공급능력을 평가 및 확인할 수 있으며, 이를 바탕으로 추가 공급 가능 범위 및 연계능력 향상을 위한 관망 설계 보완 방안을 제시할 수 있다. 이를 위해서는 제한적인 용수 공급 상황에서의 수리학적 해석기법이 요구되나, 보편적으로 사용되는 상수관망 수리해석 기법으로는 비상연계 시의 수리학적 거동을 정확히 모의할 수 없는 실정이다.
기존에 사용되는 수리해석 기법의 종류로는 Demand Driven Analysis (DDA)와 Pressure Driven Analysis (PDA)가 있다. DDA 기법은 수요량을 100% 만족시킨다는 가정 하에 수리해석을 수행하는 기법으로, 본 연구에서 모의하고자하는 비정상상황에 적용 시 비현실적인 결과를 도출한다. PDA 기법의 경우 수압과 공급가능 유량과의 관계를 고려하는 해석기법으로, DDA 기법보다 비정상상황에 대하여 신뢰도가 높다. 하지만 두 해석기법 모두 무한수원의 원칙을 적용하고 있는 바, 한정된 수원과 공급량을 반영하지 못하여 비현실적인 수리해석 결과를 도출할 수 있다. 이에 Lee et al.(2018)의 연구에 의해 기존의 PDA 수리해석 기법에 유한수원의 원칙을 적용한 Advanced Pressure Driven Analysis (A-PDA)가 제안되었다.
이에 본 연구에서는 A-PDA 수리해석 기법을 적용하여 A시의 배수지 문제발생 시, 비상연계 시나리오에 대하여 모의하였으며 기존의 DDA 및 PDA 수리해석 기법의 결과와 비교하여 현실적인 결과를 도출함을 확인하였다.
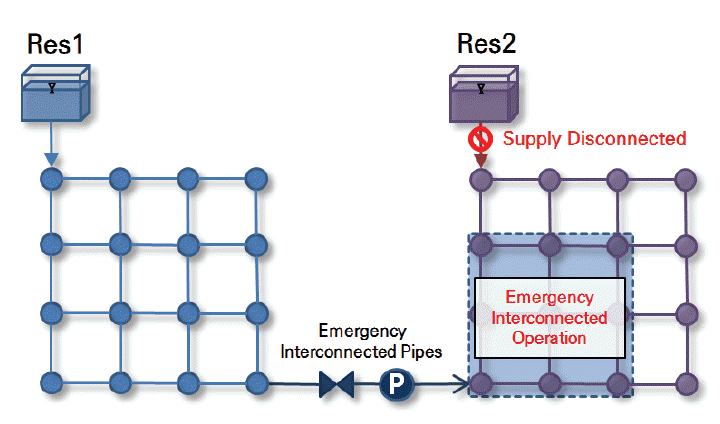
비상시 수계전환은 상수관망 시스템에서의 문제발생으로 인한 운영 중단 시, 단수 피해를 최소화하고자 인접 배수블록으로부터 용수를 연계 공급 받는 것을 의미한다. 배수블록 간에 연결된 비상관로를 통하여 비상급수가 실시되며, 이와 같은 비상시 수계 전환은 평상시에는 닫혀 있는 관로로써 필요시에만 밸브를 열어 인접배수블록으로의 공급을 가능하게 한다. 수계 전환은 광역상수도 간, 광역상수도와 지방상수도 간 및 지방상수도 간, 지방상수도 내 배수블록 간 등의 형태로 이루어지며, 해당 계획은 수리해석을 통한 상황별 모의를 바탕으로 검토될 수 있다. 다음과 같은 비상연계시스템을 도시화한 것은 Fig. 1과 같다.
상수도시설기준(2010) 7장에서는 배수시설에 대하여 인접된 수도사업자의 배수본관이나 송수관과 상호 연결하여 비상시에 상호 융통하는 것을 권장하고 있으며, 수도법 제4조에 따른 수도정비기본계획의 수립에도 연계 운영의 필요성이 명시되어 있다. 이와 같이 연계를 통한 비상공급에 대한 필요성은 인지 및 권장되고 있으며, 이에 관하여 비상연계 모의 및 연계관로 설계에 관한 연구들이 활발히 진행되고 있다.
국토부 과제인 “수직형 정수처리시설이 도입된 분산형 용수공급시스템 구축”(2014)에서는 EPANET2.0의 Emitter 기능을 이용하여 H시를 대상으로 5개의 블록 간에 가상의 비상관로를 생성하여 블록연계에 대한 수리해석을 수행하였으며, Beak et al.(2008)은 WaterGems 모형의 PDD 기능을 활용하여 J시에 대하여 7개의 대블럭에 대한 비상급수계획의 적정성을 모의하였다. Han et al.(2013)은 EPANET2.0을 활용하여 블록 간 연계관로의 수리적정성을 평가하였으며, Chang et al.(2012)는 총 부족량 기대치를 고려하여 연계관로의 합리적인 설계방안을 제시하였다. 이와 같이 기존의 연구들은 DDA 혹은 PDA 수리해석을 기반으로 수행되었다. 하지만 해당 수리해석 기법들은 무한수원의 가정을 포함하고 있어, 비상연계 공급 시 연계 배수지의 저류랑 및 유입량을 고려하지 못하고 있다. 배수지는 한정된 유량만을 저류할 수 있으며, 유입유량 또한 한정적이다. 이에 유한한 수원의 한계를 고려하여 수리해석이 모의되어야 보다 정확한 해석결과를 얻을 수 있다.
보편적으로 사용되는 상수 관망의 수리학적 해석 방법에는 수요량을 기반으로 하는 Demand Driven Analysis(DDA) 기법과, 압력 기반인 Pressure Driven Analysis(PDA) 기법이 있다. DDA는 수요량을 고정 인자로 하는 수리해석 기법으로써, 개별 절점에서 할당된 수요량을 100% 만족함을 전제로 하여 절점별 압력을 연속방정식과 순환방정식으로 계산한다. 해당 기법은 EPANET2.0(Rossman, 2000)과 KYPIPE (Wood, 2000) 등의 대부분의 상수관망 수리해석 프로그램에 적용된다. DDA 기법은 정상상태의 관망 해석에는 높은 신뢰도를 보이나, 공급유량의 부족이나 수요량의 급증과 같이 모든 절점의 수요량을 충족시킬 수 없는 비정상상황에서는 부압의 발생과 같은 비현실적인 결과를 도출한다.
PDA기법은 DDA기법에서 고려되지 않았던 절점의 압력과 공급 가능 유량 간의 상관관계를 고려하여 공급 가능 유량을 계산하는 수리해석 기법으로, 수요량의 값 또한 변수로 설정되어 HOR (Head-Nodal Outflow Relation) 관계식을 통하여 산출된다. 공급 가능 유량을 정의하는 HOR 관계식은 충족수두 이상의 수압 조건에서는 절점의 수요유량이 모두 공급 가능하고 최소수두 이하의 수압조건에서는 해당 절점에 유량 공급이 불가능하다는 개념을 포함한다(Lee et al., 2013). 즉, 절점별 압력에 따라 가능 공급량이 유동적으로 계산되므로 보다 현실적인 결과를 도출할 수 있다. HOR 관계식은 Germanopolous(1985), Wagner et al.(1988), Fujiwara and Ganshraja(1993), Gupta and Bhave(1996), Tanyimbohand Templeman(2010) 등에 의하여 제안되었으며, 실험을 통한 해당 HOR 식을 검증한 Shirzad and Tabesh(2012) 및 Jang and Kang(2014)의 연구에서는 오리피스 형태의 Wagner et al.(1998)의 연구에서 제안한 HOR식이 실험치에 가장 근사한 것을 확인하였다.
하지만 두 수리해석 기법 모두 무한수원의 가정을 포함하고 있어, 저수지로 설정된 절점에 대하여 설정된 수위를 갖는 범위 내에서 무한 공급이 가능하다. 이는 유한한 수원에 한정된 유량만이 유입되는 현실의 배수지와는 맞지 않는 가정으로, 실제 유량이 부족한 경우에도 과도한 양의 수원이 공급될 수 있어 비현실적인 수리해석 결과를 도출할 수 있다. 이에 Lee et al.(2018)에 의해 제안된 수리해석 기법은 Advanced Pressure Driven Analysis (A-PDA)로, 유한수원의 가정을 포함하여 저수지의 고갈여부 및 고갈시간에 대한 추가적인 모의가 가능하다. 이는 유한수원의 개념을 도입한 수리해석 기법으로, PDA 기법을 기반으로 저류량의 규모를 고려하여 수위-저류량 관계식을 적용하였으며 한정된 유입가능량을 고려하여 유입량 및 유입패턴 등의 변수를 추가적으로 입력할 수 있도록 하였다. 해당 기법은 상수 관망에서의 압력 저하관련 비정상상황과 저류지에서의 저류량 관련 비정상상황을 동시에 모의가능하며, 타 수리해석 기법에 비하여 비정상상황에 대한 현실적인 모의가 가능하다. 제시한 세 가지 상수관망 수리해석 기법에 대하여 Lee et al. (2018)이 제시한 특성 및 비교는 Table 1과 같다.
비상시 수계전환은 상수관망의 운영중단과 같은 비상시에 단수피해를 최소화하기 위하여 인접배수지로부터 비상공급을 실시하는 것을 의미한다. 본 연구에서는 비상시 수계전환에 대한 수리해석을 실시하고자 하는 바, 용수를 연계 공급해주는 배수지에서 기존보다 많은 유량의 용수가 요구되는 상황이다. 이에 배수지의 저류량 및 유입량이 한정적인 바, 유한수원의 한계가 고려된 A-PDA 수리해석으로 비상연계 시나리오를 모의하였다. 본 절에서는 A-PDA 수리해석 결과의 검증을 위하여, A시의 배수지 문제발생으로 인한 3개의 수계전환 시나리오에 대하여 A-PDA와 PDA 수리해석의 결과와 비교 및 분석하였다.
본 연구의 대상 지역은 약 5,628.6 ha의 면적을 포함하는 A시의 일부 구역으로(이하 A시), 3개의 동과 1개의 면을 포함한다. 3개의 배수지가 약 84,000세대에 용수를 공급하고 있으며, 각 배수블록 간의 비상관로가 설치되어 있다. A시의 관망시스템은 저수지 3개, 절점 1,492개, 펌프 8개 그리고 8개의 밸브로 구성되어 있으며, 배수지 1지-2지를 잇는 비상관 9개와 2지-3지를 잇는 비상관 1개를 포함한다. 각 배수지별 배수구역 및 비상관의 위치는 Fig. 2와 같다. 각 배수지는 개별 배수구역에 용수를 공급하는 시스템이나, 배수지에 문제가 발생할 경우 인접배수지와의 비상관로를 통해 연계 공급 받도록 한다. 각 배수지의 제원 및 특징은 Table 2와 같다.
비상시 수계전환 수리해석을 위하여 A시의 상수관망에서 배수지의 운영중단 상황을 모의하였으며, 연계 시나리오는 Table 3과 같다. 배수지에 문제 발생 모의 시, 배수관로의 상태를 Closed로 변환시켜 용수가 공급되지 않도록 설정 후 수리해석을 모의하였으며, 비상관로에 설치된 가상의 밸브를 열어 인접 배수지로부터 비상공급을 실시하였다. 유한수원의 유입유량값은 기존 관망에서 Demand Pattern이 1일 때의 저수지별 공급유량값을 사용하였다.
Table 3에 제시한 A시의 비상시 수계전환 시나리오 3개에 대하여 PDA와 A-PDA수리해석 모형을 사용하여 모의하였으며, 시간대 별로 가능한 공급량을 Eq. 1에 제시된 바와 같이 비율로써 결과 값을 계산하였다. 시나리오 1 ~ 3에 대한 모의 결과 값을 수요패턴과 함께 그래프로 도시한 것은 Figs. 3, ~ 5와 같다. 추가적으로 A-PDA 수리해석 시 유한수원의 한계로 인하여 인접 연계배수지들 또한 고갈되었으며, 배수지별 고갈 시간은 Table 4와 같다.
여기서, A c t u a l D e m a n d ( m 3 / d a y ) = ( B a s e D e m a n d + D e m a n d C a t e g o r i e s ) × D e m a n d P a t t e r n
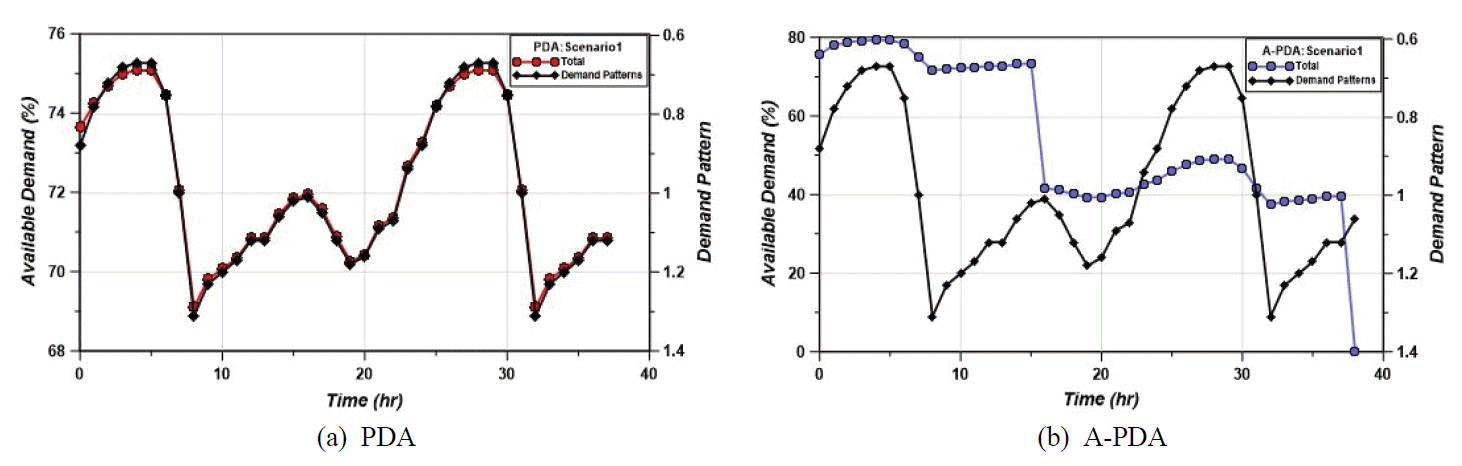
Fig. 3은 시나리오 1에 대하여 모의한 결과를 나타낸다. 이는 배수지 1지 문제발생 시, 2지와 3지로부터 용수를 비상연계 받는 시나리오로써 유한 수원의 가정이 적용된 A-PDA 수리해석의 결과(Fig. 3(b)), 2지와 3지가 각각 15:10시와 37:20시에 고갈된다. 문제발생 배수지인 1지 배수구역의 경우, 2지가 고갈되기 전인 0:00시~15:00시까지 해당 공급가능률을 수요패턴에 따라 수요량의 30~50%범위 내의 유량을 공급받는다. 하지만 3지에서 공급되는 용수는 2지 배수구역 범위를 통과해야 1지로의 공급이 가능한 바, 2지가 고갈된 후로는 1지로의 연계가 원활하지 않은 양상을 보인다. 추가적으로 1지 배수구역이 높은 지대에 위치해 있어, 타 배수지에 비하여 연계 가능한 용수가 적은 편이다. 대조적으로 PDA 수리해석은 무한수원의 가정이 적용되어, 공급가능률은 수요패턴과 같은 양상으로 나타난다. 이는 수리학적 조건이 충족될 경우, 수원의 저류용량과 관계없이 무한한 연계운영이 가능함을 보여준다.
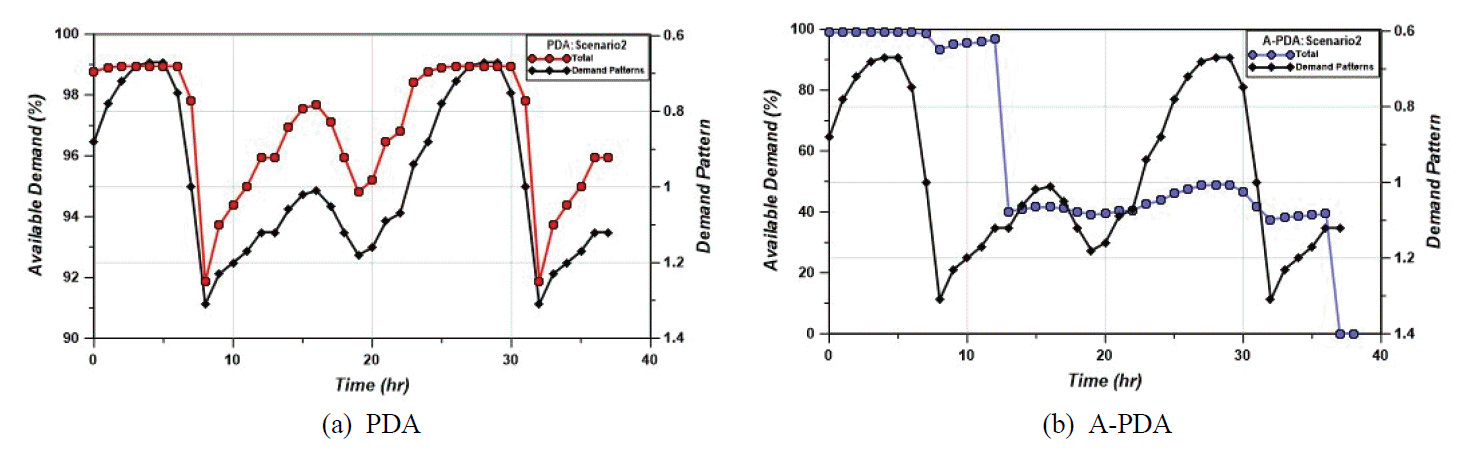
Fig. 4는 시나리오 2에 대하여 모의한 결과를 나타낸 그래프로, 2지 문제발생 시 1지와 3지로부터 연계 운영된다. A-PDA 수리해석의 결과, 1지와 3지는 각각 12:10시와 36:50시에 고갈된다. 문제발생 구역인 2지 배수구역의 경우, 1지가 고갈되는 시간 전까지 수요량의 90%이상의 용수를 공급받으며, 이후 3지가 고갈되는 시간 전까지 30%~60% 범위내의 용수를 공급받을 수 있다. 2지 배수구역의 경우 1지와 3지 배수구역 사이에 위치해 있어, 타 배수지보다 원활한 연계 공급이 가능하다. 1지 배수지의 경우 고지대에 위치해 있으며 2지 배수구역과의 비상관로가 더 많은 바, 3지보다 빠르게 고갈되는 양상을 보인다.
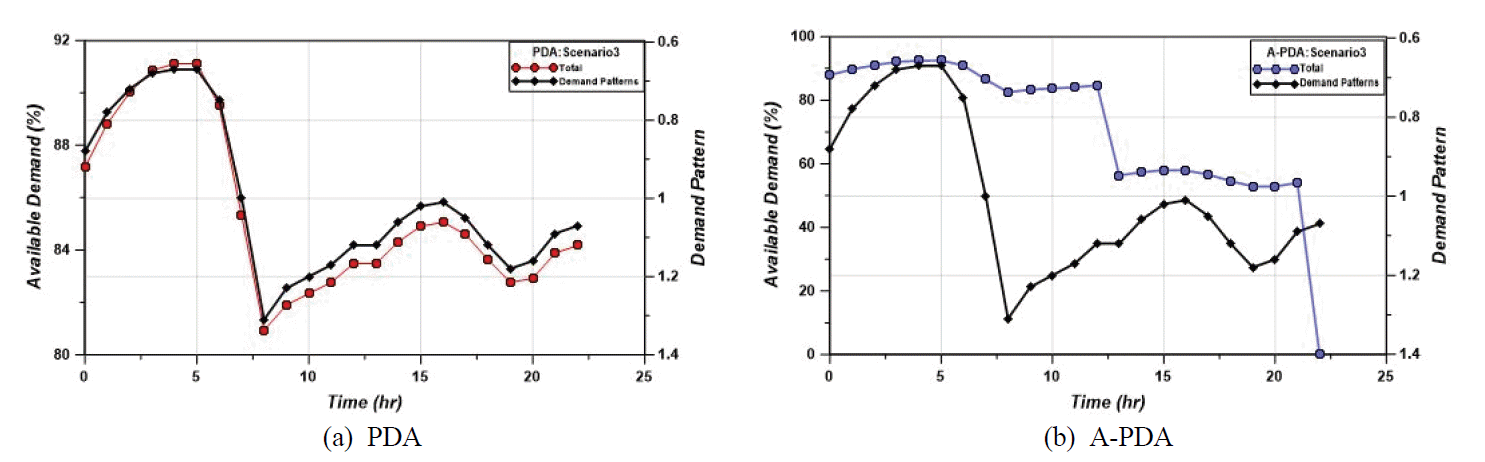
Fig. 5는 시나리오 3에 대하여 모의한 결과로, 3지 문제발생 시 1지와 2지로부터 용수를 비상연계 받는 상황이다. A-PDA 수리해석의 결과, 연계되는 배수지의 한정적인 저류용량으로 인하여 1지는 12:20시에 2지는 21:20시에 고갈되는 결과를 보여준다. 1지 배수지의 경우, 2지에 비하여 문제발생 배수지와 먼 곳에 위치하지만, 고배수지로 보다 많은 용수를 연계해주어 빠른 시간 내에 고갈된다. 3지 배수구역은 두 연계배수지가 고갈되기 전까지 수요량의 45%~65% 범위의 용수를 공급받을 수 있다.
전체적으로 PDA 모의 결과의 경우 무한수원의 법칙이 적용된 수리해석으로 공급가능율의 패턴이 수요패턴과 일치하는 양상을 보이며, 수리학적 조건이 충족될 경우 저류용량에 관계없이 무한한 공급이 이루어진다. 반면 A-PDA의 경우 급증한 수요량에 비하여 한정된 공급량으로 인해 타 배수지까지 고갈되어, 일정 시간 후에 공급가능률이 0%가 되는 결과를 보여준다. 이는 유한수원의 한계가 반영된 수리해석 결과로, 저류량의 변화 또한 고려되어 보다 현실적인 결과를 보여줌을 시사한다. 따라서, 실제 비상시 연계운영을 할 경우에 기존의 DDA 또는 PDA로 모델링하는 결과는 두 해석방법의 기본 가정인 모든 저수지의 수량은 무한이라는 가정에 의해서 현실적이지 않은 모의결과를 모의한다. 이는 비상연계 운영에 따른 전체 관망의 용수공급의 한계시점을 명확하게 예상할 수 없기 때문에 저수지 고갈에 따른 추가적인 운영상 문제에 대처할 수 있는 방안을 수립할 수 없게 한다. 이와 같은 이유로 본 연구에서 제안한 A-PDA모델의 필요성이 검증되었고 이를 활용하여 저수지 연계운영에 따른 한계시점과 한계시점을 초과하지 않게 비상시 연계 운영을 야기한 관 파괴 등에 대하여 한계시점 이전에 복구해야하는 기준 등을 수립할 수 있을 것이다. 여기서 중요한 점은 A-PDA의 적용성이다. 기본적으로 공급유량의 제한되는 점을 고려하지 않아도 되는 수리학적인 모델링(예를 들어 관경설계를 위한 모의) 등에는 DDA나 PDA모델의 활용에 문제가 없다. 그러나, 공급량이 유한이라는 가정이 반드시 필요한 경우(예를 들어 본 논문에서 제시한 비상시 연계운영)에는 보다 현실적인 모의 결과를 얻기 위해서는 A-PDA 모델의 적용이 반드시 필요하다.
본 연구에서는 상수관망의 비정상상황에서의 피해를 최소화 할 수 있는 방안인 비상시 수계전환 시나리오에 대한 수리해석을 수행하였다. 이는 기존의 비상연계에 대한 수리해석이 무한수원의 조건을 포함하고 있다는 문제점을 파악하여, 유한수원의 조건을 고려한 A-PDA 수리해석 모형을 사용하여 A시의 수계전환 시나리오를 모의하였으며 PDA 모형을 이용한 수리해석의 결과와 비교하여 현실성 높은 결과를 도출하였음을 확인하였다.
A-PDA 모형을 통한 수리해석은 기존 수리해석 모형에서는 모의가 불가능 했던 비정상상황에서의 공급가능 시간 산정이 가능하며, 이를 통하여 배수블록 간 비상연계 시 수리해석을 통하여 최대 연계 가능 시간 확인이 가능하다. 이는 비정상상황에서의 복구 및 시설물의 운용에 있어 운영자 측에 중요한 지표가 될 수 있으며, 수리해석 결과를 활용한 비상시 관망의 성능 평가 및 시간 기준에서의 평가 지표 개발 또한 가능하다. 또한 비상연계 시의 공급능력을 평가 및 확인할 수 있도록 하며, 이를 바탕으로 추가 공급 가능 범위 및 연계능력 향상을 위한 관망 설계 보완 방안을 제시할 수 있다.
본 연구는 매 0:00시에 문제가 발생하는 것으로 가정하여 수리해석을 하였지만, 매 시간마다 용수 소비 패턴이 다른 바 문제발생 시점이 중요한 인자로 작용할 수 있다. 향후 연구에서는 문제 발생 시점에 따른 수리해석 및 최대 공급 연계 가능 시간 산정을 통하여 보다 다양한 상황에서의 시스템의 거동을 파악할 예정이다.
Table 1.
Characteristic Comparisons Among Hydraulic Analysis Models (Lee et al., 2018)
Table 2.
Properties of The Reservoirs
References
Ang, W.K., and Jowitt, P.W. (2006) Solution for Water Distribution Systems Under Pressure-deficient Conditions. Journal of Water Resources Planning and Management, ASCE. Vol. 132, No. 3, pp. 175-182.

Beak, C.W., Jun, H.D., Kim, J.H., Yoo, D.K., and Lee, K.C. (2008) Evaluation of Emergency Water Supply Plan for Block System of Water Network using WaterGEMS. J. Korean Soc. Hazard Mitig., Vol. 8, No. 6, pp. 15-20.
Bhave, P.R. (1991). Analysis of Flow in Water Distribution Networks. Technomic Publishing.
Chang, Y., Kim, J., and Jung, K. (2012) A Study on the Design and Evaluation of Connection Pipes for Stable Water Supply. Journal of Korean Society of Water and Wastewater, Vol. 26, No. 2, pp. 249-256.


Fujiwara, O., and Ganesharajah, T. (1993) Reliability Assessment of Water Supply Systems with Storage and Distribution Networks. Water Resources Research, Vol. 29, No. 8, pp. 2917-2924.


Germanopoulos, G. (1985) A Technical Note on the Inclusion of Pressure Dependent Demand and Leakage Terms in Water Supply Network Models. Civil Engineering Systems, Vol. 2, No. 3, pp. 171-179.

Han, W., Jung, K., and Kim, J. (2013) Hydraulic Adequacy of Connection Pipes in Water Supply Systems for Contingencies. Journal of Korean Society of Water and Wastewater, Vol. 27, No. 6, pp. 679-687.


Jang, D., and Kang, K. (2014) Experimental Analysis of Nodal Head-outflow Relationship Using a Model Water Supply Network for Pressure Driven Analysis of Water Distribution System. J. Korean Soc. Environ. Eng., Vol. 36, No. 6, pp. 421-428.

Korea Water and Wastewater Works Association (2010). Water Supply Facilities Criteria.
Lee, H.M., Jun, H., Baek, S.C., and Kim, J.H. (2018) Development and Application of Advanced-Pressure Driven Analysis Model Considering Limited Reservoir. J. Korean Soc. Hazard Mitig., Vol. 18, No. 2, pp. 271-280.


Lee, H.M., Yoo, D.G., Kim, D.Y., and Kim, J.H. (2013) Development and Application of Pressure Driven Analysis Model based on EPANET. J. Korean Soc. Hazard Mitig., Vol. 13, No. 4, pp. 121-129.


Ministry of Environment Korea (2015). Statistics of Water Supply and Sewage System.
Rossman, L.A. (2000). EPANET 2: Users Manual. US Environmental Protection Agency, Cincinnati, OH.
Shirzad, A., and Tabesh, M. (2012). Study of Pressure- Discharge Relations in Water Distribution Networks Using Field Measurements. Proceedings of the IWA World Water Congress & Exhibition. Busan, Korea.
Tanyimboh, T.T., and Templemen, A.B. (2010) Seamless Pressure-deficient Water Distribution System Model. Proceedings of the Institution of Civil Engineers - Water Management, Vol. 163, No. 8, pp. 389-396.

Wagner, J.M., Shamir, U., and Marks, D.H. (1988) Water Distribution Reliability: Simulation Methods. Journal of Water Resources Planning and Management, Vol. 114, No. 3, pp. 276-294.

Walski, T.M. (1993) Practical Aspects of Providing Reliability in Water Distribution Systems. Reliability Engineering & System Safety, Vol. 42, No. 1, pp. 13-19.

Wood, D.J. (1980). Computer Analysis of Flow in Pipe Networks Including Extended Period Simulations: User's Manual. Office of Continuing Education and Extension of the College of Engineering of the University of Kentucky.
- TOOLS
-
METRICS

-
- 3 Crossref
- 4,411 View
- 68 Download
- Related articles in KOSHAM
-
Application of the Fuzzy Models for the Efficient Operation of Pumping Station2004 September;4(3)