1. 서론
최근 들어 우리나라를 비롯한 미국, 유럽, 남미국가에서는 지구 온난화에 따른 슈퍼 엘리뇨(적도 해수면 온도 상승)현상으로 자연재해(특히, 홍수피해)가 크게 증가하고 있고 그 피해 규모 또한 대형화⋅다양화되고 있는 추세이다(CHANNEL A Comprehensive News, 2015. 12. 31). 이 같은 자연재해에 대비하여 우리나라에서는 2006년부터 하나의 시⋅군⋅구를 하나의 보험요율산정단위로 하는 풍수해보험을 정책보험1으로 운용하고 있다. 그러나 2016년 10월 태풍 18호 차바(CHABA)로 울산광역시 북구를 가로지르는 태화강 유역을 중심으로 침수피해가 많이 발생했다는 것은 지역별 위험도와 관계없이 단순히 행정단위(시⋅군⋅구)를 기준으로 동일한 보험요율을 적용하고 있는 현행 풍수해보험 요율의 산정 및 검증방법에 대한 합리성 검토가 필요하다는 것을 말해주고 있다. 먼저, 풍수해보험 요율의 산정 측면에서 볼 때 보험업법 제129조(보험요율 산출의 원칙) 제3호에서 규정하고 있는 ｢보험요율은 보험계약자 간에 부당하게 차별적이지 않도록 산정되어야 한다.｣라는 공정성의 원칙에 부합되는 가에 대한 합리성 검토가 필요하다. 예를 들면, 현행 풍수해보험 요율산정 방법에 의하면 울산광역시 북구에 위치하고 있는 모든 보험가입목적물은 지역별(예, 고지대 또는 저지대) 위험도와 관계없이 동일한 보험요율이 적용되고 있다. 따라서 현행과 같은 보험요율 산정방법은 풍수해보험법 제11조(보험료율의 산정)의 제3호에서 규정하고 있는 ｢풍수해보험관리지도에 표시된 위험정도에 따라 지역별로 보험요율을 다르게 적용할 것｣이라는 보험요율의 산정원칙(공정성의 원칙)과 배치된다고 볼 수 있다. 다음으로, 풍수해보험 요율의 검증 측면에서 볼 때 보험요율 검증의 기준이 되는 손해율(Loss Ratio)을 추정함에 있어 보험요율산정가의 주관적 판단(범위모수, 확률수준 등)에 의존하는 변동제한법(Limited Fluctuation Approach)에 의한 신뢰도(Credibility)를 적용하고 있다는 점이다.
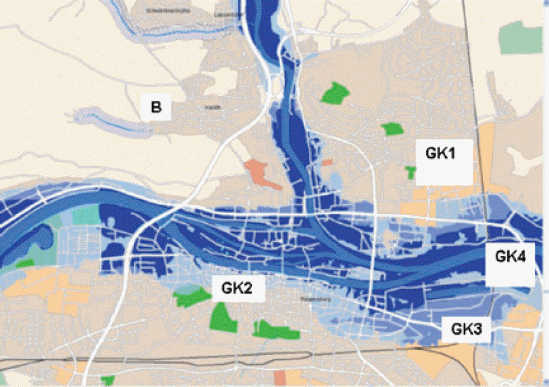
풍수해보험요율 산정과 관련해서 Lee (2016)는 통계적인 분포를 이용해서 4개의 위험등급별 보험요율을 산정하였고, Lee et al. (2016)는 수해⋅풍해⋅설해위험도를 반영한 위험등급별 보험요율 산정 알고리즘을 제안하였다. Shin (2005)은 독일 홍수보험의 위험등급별 요율산정방법을 소개하고 있다. 특히, 독일에서는 Fig. 1에서 보는 바와 같이 지역별 위험정도(심도)와 발생빈도(10년: GK4, 50년: GK3, 200년: GK2, 500년: GK1)에 따라 4개의 위험등급체계로 보험요율을 산정⋅적용하고 있는 것으로 나타났다.
풍수해보험요율 검증과 관련해서 Lee et al. (2001)는 Bühlmann-Straub의 경험적 베이즈 신뢰도 모델을 이용해서 손해율을 추정하였고, Lee et al. (2002)는 위험등급 간 평균의 분산값τ2이 항상 양수가 되는 새로운 Bühlmann- Straub의 경험적 베이즈 신뢰도 모델을 제안하였다. KIDI (2011)는 풍수해보험을 포함해서 일반적인 재물보험의 손해율 추정방법을 제시하였다. 본 연구에서는 풍수해보험 요율을 산정함에 있어 공정성의 원칙이 적용될 수 있도록 현행 시⋅군⋅구 단위의 보험요율산정단위를 동질위험집단(Homogeneous Risk Group)으로 등급화해야 하는 당위성을 통계적인 방법을 통해 확인하였고, 풍수해보험요율의 검증기준이 되는 손해율을 추정함에 있어 변동제한법에 의한 신뢰도보다는 Bühlmann- Straub의 경험적 베이즈 신뢰도가 보다 더 합리적이라는 사실을 실증적 사례분석을 통해 확인하였다. 이를 위해 제2장에서는 현행 풍수해보험요율의 산정 및 검증방법에 대한 합리성을 검토하였고 이를 뒷받침해주는 통계적인 방법을 제3장과 제4장에서 기술하였다. 제3장에서는 보험요율의 합리적인 차별화를 위해 위험등급의 동질성 여부를 검증할 수 있는 Kruskall-Wallis의 위험등급별 동질성 검정 방법을 제안하였고, 제4장에서는 현재 풍수해보험요율 검증 시 적용되는 변동제한법에 의한 신뢰도를 구체적으로 살펴보고 보험요율산정가의 주관적 판단이 배제되는 새로운 형태의 Bühlmann-Straub의 경험적 베이즈 신뢰도 방법을 제안하였다. 제5장에서는 제3장과 제4장에서 제안한 통계적 방법을 이용한 실증적 사례분석을 통해 위험등급화의 당위성과 Bühlmann-Straub의 경험적 베이즈 신뢰도의 적용 가능성을 확인하였다.
2. 현행 풍수해보험요율의 산정 및 검증방법에 대한 합리성 검토
2.1 현행 풍수해보험요율의 산정방법에 대한 합리성 검토
2.1.1 현행 풍수해보험요율의 산정방법
일반적으로 보험요율의 산정이라 함은 보험종목별 또는 위험적용단위별로 순보험료(Pure Premium)와 부가보험료(Loading Premium)를 계산하여 영업보험요율(Gross Premium Rate)을 산출하거나 이를 조정하는 것을 말한다. 현행 풍수해보험에서는 전국 232개 시⋅군⋅구 각각을 하나의 보험요율산정단위로 동일한 보험요율을 산정⋅적용하고 있다. 따라서 현행과 같은 풍수해보험 요율의 산정방법은 보험업법 제129조(보험요율의 산출원칙) 제3호에서 규정하고 있는 ｢보험요율은 보험계약자간에 부당하게 차별적이지 않도록 산정되어야 한다.｣라는 공정성의 원칙(Not Unfairly Discriminatory)에 크게 어긋나고 있음을 알 수 있다. 예를 들면, 경기도 평택시의 경우 100년(재현기간) 빈도 홍수발생시 현덕면 소재 시설물의 피해율은 0.4%인데 비해 서탄면 소재 시설물의 피해율은 27.4%로 무려 68.5배가 큼에도 불구하고 평택시에 위치하고 있는 모든 보험가입목적물에 대해서 보험가입목적물이 어디에 위치(예를 들면, 고지대 또는 저지대)하고 있건 관계없이 단순히 행정단위를 기준으로 동일한 보험요율을 산정⋅적용하고 있다는 점이다. 다시 말해, 보험가입목적물이 위치하고 있는 지역별 위험도가 반영되고 있지 않다는 점이다. 따라서 현재 풍수해보험 가입자 중에서 위험이 적은 지역(예, 고지대)에 보험가입목적물이 위치하고 있음에도 불구하고 상대적으로 많은 보험료를 내고 있는 보험가입자가 발생하게 되고, 반대로 위험이 큰 지역(예, 저지대)에 위치하고 있는 보험가입목적물을 소유하고 있는 보험가입자는 상대적으로 적은 보험료를 내게 됨으로써 현행과 같은 보험요율산정방법 하에서는 보험가입자의 역선택(Anti- Selection) 문제를 야기할 가능성이 커지게 된다. 결국, 위험도가 낮은 지역의 보험가입자가 위험도가 높은 지역의 보험가입자에게 보험료를 간접적으로 보조하는 형태가 되고 있다(Lee et al., 2016).
2.1.2 현행 풍수해보험 요율산정 방법에 대한 합리성 검토
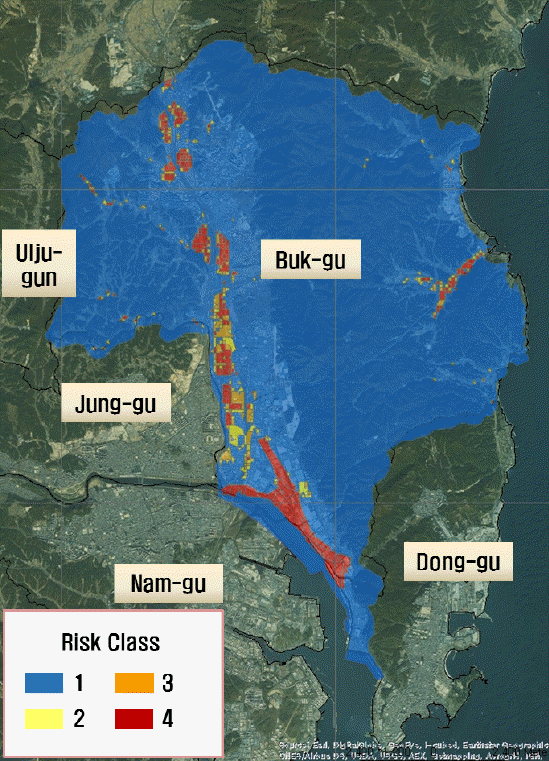
이처럼 232개 시⋅군⋅구 각각을 하나의 요율산정단위로 적용한다는 것은 지역별 위험도에 따른 합리적인 보험요율차별화가 이루어지지 않고 있다는 것을 말해주고 있다. 따라서 본 연구에서는 ‘풍수해보험법 제11조(보험요율의 산정)’ 제3호에서 규정하고 있는 지역별 위험도에 따라 보험요율을 합리적으로 차별화 할 수 있도록 보험요율산정단위를 침수심에 따라 4개의 위험등급으로 동질위험집단화하는 방안을 제안하였다. 예를 들면, 울산광역시 북구의 위험등급별 침수심 및 침수면적(Table 1)을 지도상에 나타낸 분포도는 Fig. 2와 같다. Table 1과 Fig. 2에서 보는 바와 같이 울산광역시 북구의 대부분 지역이 위험도가 낮은 1등급 (침수심 D=0cm) 지역으로 나타나고 있다.
Table 1
Inundation Depth, Area by Risk Class in Buk-gu, Ulsan City
| Risk Class | 1 | 2 | 3 | 4 | Total |
|---|---|---|---|---|---|
| Inundation Depth(D) | D = 0cm | 0cm < D ≤ 50cm | 50cm < D ≤ 100cm | 100cm < D | |
| Inundation Area(km2) | 157.00 | 1.96 | 2.00 | 3.32 | 164.28 |
현행 풍수해보험요율 산정방법에 대한 합리성을 분석하기 위해 제3장에서는 손해율을 확률변수로 하는 Kruskall- Wallis의 위험등급별 동질성 검정방법을 제안하였고 5.2절에서는 2008년부터 2014년까지의 풍수해보험의 연도별 계약 및 손해상황 데이터(손해율)을 이용하여 위험등급별 보험요율 차등화의 타당성을 확인하였다.
2.2 현행 풍수해보험요율의 검증방법에 대한 합리성 검토
2.2.1 현행 풍수해보험요율의 검증방법
일반적으로 보험요율의 검증이라 함은 장래의 적정한 보험요율 수준을 예측할 수 있도록 보험요율을 구성하고 있는 손해율과 사업비율 및 이익률에 대한 과거의 실적을 집계⋅분석하는 것을 말한다. 특히, 손해율은 보험원가를 구성하는 매우 중요한 보험요율산정 변수이다. KIDI (2011)에 따르면 손해율2은 다음과 같은 Eq. (1)로 추정하고 있는 것으로 조사되었다. 여기서, 가중치 반영 손해율3은 최근년도에 더 많은 가중치를 부여한 손해율을 말하고Z는 신뢰도(Credibility)를 말한다. 또한 신뢰도의 보수는 위험등급을 구분하지 않은 상위등급의 전체 손해율을 말한다. Eq. (1)에 의한 손해율의 추정방법에 대해서는 5.3.1절에서 실제 사례를 들어 자세하게 분석하였다.
2.2.2 현행 풍수해보험 요율의 검증방법에 대한 합리성 검토
현행과 같은 추정손해율 산정 Eq. (1)에 적용되는 요소들 각각이 보험요율산정가의 주관적 판단에 따라 결정된다는 점이다. 즉, 가중치 반영 손해율은 최근년도(Current Year)의 정보에 더 많은 가중치를 부여하기 위한 것으로 보험요율산정가의 주관적 판단에 따라 결정되고 있고 신뢰도Z역시 보험요율산정가의 주관적인 판단(범위모수k, 확률수준P)에 따라 결정되는 변동제한법(Limited Fluctuation Approach)을 적용하고 있다는 점이다. 신뢰도의 보수는 과거 년도(Old Year)의 정보를 반영하기 위한 것으로 상위등급의 전체 손해율을 임의적으로 적용하고 있다는 점이다. 이처럼 현행과 같은 손해율 추정방법은 보험요율산정가의 주관적 판단에 따라 결과치가 크게 좌우될 수 있다는 문제점을 갖고 있다.
현행 풍수해보험요율 검증방법에 대한 합리성을 분석하기 위해 본 연구에서는 신뢰도Z를 중심으로 보험요율산정가의 주관적인 판단이 배제된 손해율 추정방법을 제안하였다. 먼저, 현재 실무에서 적용하고 있는 ｢4.1 변동제한법에 의한 위험등급별 손해율의 추정방법｣은 보험요율산정가의 주관적 판단에 따라 추정치가 크게 달라질 수 있다는 점을 확인하였다. 다음으로 ｢4.2 Bühlmann-Straub의 경험적 베이즈 신뢰도를 이용한 위험등급별 손해율의 추정방법｣에서는 보험요율산정가의 주관적 판단이 배제되는 Bühlmann-Straub의 경험적 베이즈 신뢰도의 실체를 분석함으로써 손해율이 객관적으로 추정될 수 있다는 점을 확인하였다. 5.3절에서는 이들 두 방법에 대한 실증적 사례분석을 통해 Bühlmann-Straub의 경험적 베이즈 신뢰도에 의한 추정손해율이 주관적인 판단을 배제할 수 있을 뿐만 아니라 적합도 검증결과 Bühlmann-Straub의 경험적 베이즈 신뢰도가 변동제한법에 의한 추정결과 보다 합리적이라는 점을 확인하였다.
3. Kruskall-Wallis의 위험등급별동질성 검정방법
Kruskall-Wallis의 위험등급별 동질성 검정방법은 모집단이 정규분포를 따른다는 가정을 할 수 없을 때 순위(Ranks)를 이용해서 위험등급 간 이질성의 정도, 즉, 위험등급별 보험요율차등화의 타당성을 검정하는 방법이다. 일반적으로 Kruskall-Wallis 검정방법은n = n1 + n2 + … + nK개의 실험단위들을 표본의 크기가n1, n2, … nK,인K개의 위험등급으로 랜덤하게 나누어, 각 위험등급에 처리 1, 2, …, K가 적용된다고 할 때 이들K개의 위험등급 효과가 모두 같은 가를 검증하는 방법이다. 즉, 귀무가설(H1)과 대립가설(H0)은 다음과 같다.
H0: 연속인K개의 모집단은 동일하다.
H1: K개 모집단이 모두 동일하지 않다
이와 같은 모형을 분포함수로 나타내면 다음과 같다. 즉, i=1, 2, …, K에 대하여 각 등급별 손해율Xi1, Xi2, …, Xin는 연속분포F(x−μi)에서의 서로 독립인 확률표본이라 할 때 일원배치법에서의 자료구조를 정리하면 Table 2와 같다. 여기서, 총표본크기 n = ∑ i = 1 K n i
Table 2
Data Configuration of One-Way ANOVA
| Risk Class | 1 | 2 | … | K |
|---|---|---|---|---|
| Data | ||||
| 1 | X11 | X21 | … | XK1 |
| 2 | X12 | X22 | … | XK12 |
| … | … | … | … | … |
| ni | X1n1 | X2n2 | … | XKnK |
K개의 모집단에서 얻은n = n1 + n2 + … + nK개의 관측 값으로 혼합표본을 만든 다음, 각 위험등급 내에서 작은 것부터 크기순으로 순위를 부여한다. 혼합표본에서의 손해율Xij의 순위(Ranks)를Rij라 했을 때, Xij대신에 그의 순위인Rij로 대체하여 Table 3을 작성한다.
Table 3
Ranks of Blended Sample
| Risk Class | 1 | 2 | … | K |
|---|---|---|---|---|
| Classification | ||||
| Ranking by Risk Class | R11 | R21 | … | RK1 |
| R12 | R22 | … | RK2 | |
| … | … | … | … | |
| R1n1 | R2n2 | … | RknK | |
| Rank’s Sum. | W1 | W2 | … | WK |
| Mean Rank |
|
|
… |
|
혼합표본에서의 순위를 이용하여 각 위험등급별 순위 합을 W i = ∑ j = 1 n i R i j R i ¯ = 1 n i ∑ j = 1 n i R i j = W i n i R i ¯ = 1 + 2 + ... + n n = n + 2 2 n + 2 2
기대된다. 한편, (R 1 ¯ − n + 1 2 R 2 ¯ − n + 1 2 R K ¯ − n + 1 2 H = 12 n ( n + 1 ) ∑ i = 1 K n i ( R 1 ¯ − n + 1 2 ) 2
4. 신뢰도(Credibility)를 이용한 위험등급별 손해율의 추정방법
4.1 변동제한법에 의한 위험등급별 손해율의 추정방법
변동제한법에 의한 위험등급별 신뢰도는 확률적 변동을 일정한 한도로 제한하는 방법으로 빈도학파 또는 고전적인 패러다임(Frequentist or Classical Paradigm)에 의해 전개되는 신뢰도 이론이다. 변동제한법에서는 신뢰도를 전신뢰도(Full Credibility)와 부분신뢰도(Partial Credibility)로 나누고 있다. 본 절에서는 I. B. Hossack et al. (1999)에서 기술하고 있는 변동제한법에 의한 신뢰도 이론을 본 연구에 맞게 분석⋅인용하였다.
4.1.1 기본가정
변동제한법에 의한 전신뢰도와 부분신뢰도를 전개하기 위해서는 다음과 같은 기본가정들이 필요하다. 첫째, 총 사고건수는N으로, 이것은 어떤 주어진 기간 동안(예를 들면, 보험기간 1년) 보험포트폴리오 내에서 발생하는 총사고건수를 나타내는 확률변수이다. 보통 확률변수N은 포아송분포, 이항분포 등을 가정할 수 있겠으나 여기에서는 확률변수N이 모수가n인 포아송분포를 따른다고 가정한다. 둘째, 주어진 보험포트폴리오 내에서 발생하는 사고건수에 대한i번째 손해액의 크기를 나타내는 확률변수를Li, (i=1, 2, 3, …, N)로 나타내고Li들은 모평균이μ이고 모분산이σ2인 동일한 분포를 따른다고 가정한다. 셋째, 확률변수N과 확률변수L1, L2, …, LN은 서로 독립이라고 가정한다. 이와 같은 기본 가정 하에서 보험포트폴리오 내에서 일정기간 동안에 발생하는 총손해액은L = L1 + L2 + … + LN으로 나타낼 수 있으며, 이때 총손해액L의 모평균과 모분산은 각각E(L) = nμ과Var (L) = (σ2 + μ2)가 된다.
4.1.2 전신뢰도(Full Credibility)
전신뢰도는 최근 정보량을 100% 신뢰할 수 있을 때 부여되는 신뢰의 정도를 말한다. 변동제한법에 의한 전신뢰도의 기본 개념은 위 4.1.1절의 기본가정들을 전제로 추정량과 모수와의 차이를 일정한도로 제한하는 방법이다. 다음과 같이 3단계의 과정을 거쳐 전신뢰도에 필요한 최소사고건수를 구한다.
<1단계> 확률P에 대하여 부등식Pr (| L−E(L) | ≤ kE(L)) ≥ P가 성립하는 최소의n의 값을nF라고 놓는다. 여기서, k는 범위모수이고P는 확률수준(Probability Level)이다.
<2단계> 다음과 같은 표준화된 식에 중심극한정리(Central Limit Theorem)를 적용한다.
표준화된 식 L − E ( L ) V a r ( L ) k E ( L ) V a r ( L ) ≥ Φ − 1 ( 1 − α / 2 )
<3단계> Eq. (2)에 의해 다음과 같은 전신뢰도를 만족시키는 식이 성립한다.
Eq. (3)의 총손해액의 기댓값E(L) = nμ과 분산값Var (L) = n (σ2 + μ2)을 각각 대입하여n에 대해 풀면n의 최소값으로써 전신뢰도를 만족시키는 사고건수nF가 구해진다. 여기서, CV는 변동계수(Coefficient of Variation)를 말한다.
실제로 Eq. (4)를 이용하여 전신뢰도에 필요한 사고건수nF를 계산하기 위해서는 손해액 데이터로부터 모평균μ와 모분산σ2을 추정하지 않으면 안된다. 만약, 각 손해액의 크기가 동일한 경우(즉, CV=0인 경우) 범위모수k와 확률수준1 − α에 해당하는 전신뢰도에 필요한 최소사고건수는 Table 4와 같다. KIDI (2011)에서는 범위모수(k) 0.1이고 신뢰수준(P) 0.95일 때 전신뢰도에 필요한 사고건수 384*를 기준으로 손해율을 추정하고 있는 것으로 나타났다.
4.1.3 부분신뢰도(Partial Credibility)
부분신뢰도는 주어진 최근 정보량을 100% 신뢰할 수 없을 때 부여되는 신뢰의 정도를 말하는 것으로 전신뢰도와 마찬가지로 위 4.1.1절의 기본가정들을 만족시킨다고 가정할 때, 부분신뢰도를 산정하는 단계는 다음과 같다.
<1단계> 부분신뢰도 (Zp)가 가중된 총손해액의 추정치ZpL − (1−Zp)E(L)와 총손해액의 기대값E(L)의 차이가kE(L)내에 있을 확률이P이상이 되도록 한다. 즉, Pr [| ZpL−ZpE(L) | ≤ kE(L) ≥ P가 된다.
<2단계> 다음과 같은 표준화된 식에 중심극한정리를 적용한다.
<3단계> 중심극한정리(Central Limit Theorem)에 따라 L − E ( L ) Z p V a r ( L ) )
Eq. (6)을Zp에 대해 풀면 다음과 같은 부분신뢰도(Zp) 산출모델이 된다.
Eq. (7)에E(L) = nμ과Var (L) = n (σ2 + μ2)를 각각 대입하여 풀면 다음 Eq. (8)과 같이 전신뢰도에 필요한 사고건수(nF)와 실제 사고건수(n)와의 관계식이 성립한다. 이것이 우리나라에서 보험요율을 검증할 때 주로 사용하는 부분신뢰도의 산정공식이다.
여기서, n과nF는 실제사고건수와 전신뢰도에 필요한 최소사고건수를 각각 말하고, μ와σ는 손해액의 모평균과 모표준편차를 각각 말한다. 또한ϕ−1(1−α/2)와k는 전신뢰도의 경우와 동일하다. 이 같은 부분신뢰도를 이용하여 Eq. (9)와 같은 형태로 손해율을 추정한다. 여기서, X ^ L F A
이와 같이 우리나라에서 주로 사용하고 있는 변동제한법에 의한 신뢰도는 범위모수k와 확률수준P를 보험요율산정가가 주관적으로 결정해야만 한다. 따라서 범위모수k와 확률수준P를 어떻게 결정하느냐에 따라 전신뢰도에 필요한 최소사고건수의 크기가 달라질 수 있다는 점이다. 또한 위험도를 판단하는 요소로 사고건수뿐만 아니라 손해액, 보험가입금액, 보험료 등을 고려할 수 있으나 변동제한법에 의한 신뢰도는 사고건수의 크기만을 고려하고 있다는 점이다. 이 같은 주관적인 판단 등을 배제하기 위해 개발된 신뢰도 모델이 Bühlmann-Straub의 경험적 베이즈 신뢰도이다.
4.2 Bühlmann-Straub의 경험적 베이즈 신뢰도를 이용한 위험등급별 손해율의 추정방법
Bühlmann-Straub의 경험적 베이즈 신뢰도를 이용한 위험등급별 손해율의 추정방법은 개별경험치의 안정성의 정도(Degree of Stability)를 반영하기 위한 변동제한법과 달리 위험등급별 이질성의 정도(Degree of Heterogeneity)를 반영하기 위한 손해율 추정방법이다. 일반적으로 Bühlmann-Straub의 경험적 베이즈 신뢰도는 Eq. (12)와 같은 형태로 나타난다. 본 절에서는 Lee et al. (2001)에서 제안하고 있는 Bühlmann -Straub의 경험적 베이지안 신뢰도를 본 연구에 맞게 분석⋅인용하였다. 다만, Lee et al. (2001)에서는 일반적인 위험단위수(Eit)로 사고건수(Nit)와 보험료(Pit)만을 적용하였으나 본 연구에서는 손해액(Lit)을 추가적으로 적용하였다. 여기서i = 1, 2, …, K, 는 위험등급을 말하고t, t = 1, 2, …, T(i)는 통계기간을 말한다. 베이지안 방법에 의한 신뢰도에서는 모수를 하나의 확률변수로 취급하여 이에 대한 주관적인 판단 또는 사전적인 정보(분포)를 이용하여 모수를 추정하지 않으면 안된다. 따라서 베이즈 방법에 의한 신뢰도를 적용하기 위해서는 모든 분포를 완전하게 알아야만 한다. 일반적으로 베이지안 추정량을 정하기 위한 사후분포를 찾기가 어렵고 사후분포를 찾았다고 하더라도 사전분포를 정규분포로 가정한다는 것은 보험요율산정가의 주관적인 판단에 따를 수밖에 없다는 한계점이 있다. 이 같은 순수 베이즈 이론에 의한 신뢰도 산정의 어려움을 극복하기 위해 도입된 것이 Bühlmann-Straub의 경험적 베이즈 신뢰도이다. Bühlmann- Straub의 경험적 베이즈 신뢰도 모델을 전개하기 위해서는 Table 5와 같은 보험포트폴리오가 필요하다. Table 5에서 보는 바와 같이XiT(i)와EiT(i)는 위험등급i의T(i)년도의 손해율과 일반적인 위험단위를 각각 나타낸다. 위험등급은K개로 구성되었다. 즉, i = 1, 2, …, K이다.
Table 5
Configuration of Insurance Portfolio
Table 5에서Θi는 확률변수로 위험등급i의 위험모수를 나타내며μ(Θi)과σ2(Θi)는i번째 위험등급의 모평균과 모분산의 함수를 각각 나타낸다. 관측치들과 모수들 간에는 다음과 같은 가정들이 필요하다.
<가정 1> 고정된 위험모수Θi, i = 1, 2, …, K, 가 주어질 때 확률변수Xi1, Xi2, …, Xi(T)i는 서로 독립이다. 또한E[X | Θi] = μ(Θi)이고 V a r ( X | Θ i ) = σ 2 ( Θ i ) E i t
<가정 2> 고정된 모수Θ1, Θ2, …,ΘK가 주어질 때i ≠ j에 대하여 확률벡터 (Xi1, Xi2, …, Xi(T)i)와 (Xj1, Xj2, …, Xj(T)j)는 서로 독립이다. 또한 위험모수Θ1, Θ2, …,ΘK는 서로 독립이고 동일한 분포를 따른다.
<가정 3> 확률변수Eit의 분산은 유한하다.
위에서 언급한 바와 같이 일반적으로 순수 베이즈 이론에 의한 신뢰도를 계산하기 위해서는 모수Θ에 대한 사전분포를 주관적으로 결정하지 않으면 안된다. 그러나 4.2.1절과 4.2.2절에서 보는 바와 같이 Bühlmann-Straub의 경험적 베이즈 신뢰도에서는 위험모수Θ의 사전분포와 확률변수x의 조건분포f(x/θ)를 모르더라도 경험데이터로부터 각 위험등급별 신뢰도를 산정할 수 있다.
4.2.1 위험등급 내 분산의 기댓값Σ2의 추정
위의 <가정 1>∼<가정 3>하에서 위험등급 내 분산의 기댓값Σ2의 불편추정량은 Eq. (10)과 같다. 위험등급 내 분산의 기댓값Σ2의 추정식 Eq. (10)의 증명은 Lee et al. (2001)에서 기술하고 있다.
4.2.2 위험등급 간 평균의 분산값τ2의 추정
위의 <가정 1>∼<가정 3>하에서 위험등급 간 평균의 분산값τ2의 불편추정량은 Eq. (11)과 같다. 위험등급 간 평균의 분산 값τ2의 추정식 Eq. (11)의 증명은 Lee et al. (2001)에서 기술하고 있다.
여기서, W = ∑ i = 1 K ∑ t = 1 T ( i ) E i t E .. ( X i t − X .. ¯ ) 2 τ 2 ^ τ 2 ^ Z i ( B S )
따라서 위험등급i의 Bühlmann-Straub의 경험적 베이즈 신뢰도 Z i ( B S ) X .. ¯ ( Z i )
이처럼 Bühlmann-Straub의 경험적 베이즈 신뢰도의 가장 큰 특징은 순수 베이지안(Exact Bayesian)의 방법에 의한 신뢰도와 달리 사전분포(Prior Distribution)를 보험요율산정가의 주관적 판단이 아닌 과거의 경험데이터로부터 찾는 데 있다. Bühlmann-Straub의 경험적 베이즈 신뢰도를 산정하기 위한 데이터와 수식들을 하나의 통일된 기호로 정리하면 다음과 같다.
데 이 터
Pit = 위험등급 i의 t년도 보험료,
Pit = 위험등급 i의 t년도 사고건수,
Lit = 위험등급 i의 t년도 손해액,
Eit = 위험등급 i의 t년도 일반적인 위험단위수,
위와 같은 데이터를 가지고 Bühlmann-Straub의 경험적 베이즈 신뢰도가 반영된 위험등급별 손해율을 추정하기 위해 필요한 수식들은 다음과 같다. 여기서, 가중치로 일반적인 위험단위수(Eit)를 사용하였다.
수 식
Bühlmann-Straub의 경험적 베이즈 신뢰도 산정에 적용되는 데이터의 구조는 Table 6과 같다.
Table 6
Data Structure Required for Empirical Bayes Credibility of Bühlmann-Straub
Eqs. (10)∼(13)에 의해 위험등급별 Bühlmann-Straub의 경험적 베이즈 신뢰도가 반영된 손해율을 추정하기 위해서 다음과 같이 5단계에 걸친 계산이 필요하다. 이하에서, i = 1, 2, …, K이고T(i)는 통계기간, K는 위험등급수를 각각 나타낸다.
<Step 1> 위험등급 내 분산의 기댓값Σ2의 추정
Table 6과 같이 일반적인 위험단위수(Eit)를 가중치로 한 위험등급i의 평균손해율(X i ¯ ⋅ ∑ i 2 ^
Eq. (14)에 의해 구한 각 위험등급 내 분산들의 합을 위험등급 수K로 나누어 위험등급 내 분산의 기대 값의 추정치를 Eq.(10)′과 같이 구한다. 즉,
<Step 2> 위험등급 간 평균의 분산 값τ2의 추정
Eq. (11)′에 의해 위험등급 간 평균의 분산 값의 추정치 τ 2 ^ W = ∑ i = 1 K ∑ t = 1 T ( i ) E i t E ... ( X i t − X ¯ .. ) 2
<Step 3> 위험등급 내 분산의 기댓값의 추정치 ∑ ^ 2 τ ^ 2 Z i ( B S )
<Step 4> 위험등급별 신뢰도를 가중치로 한 전체 평균손해율(X .. ¯ ( Z i )
<Step 5> 위험등급i의 Bühlmann-Straub의 경험적 베이즈 신뢰도 Z i ( B S ) X ^ i ( B S )
위험등급별 Bühlmann-Straub의 경험적 베이즈 신뢰도 Z i ( B S ) X i ⋅ ¯ i X .. ( Z i ) X i ^ ( B S )
5. 실증적 사례분석
5.1 분석데이터
본 절에서는 GIS(Geographic Information System)에 의해 지역별로 위험등급 분류가 가능4한 서울특별시 강서구, 인천광역시 강화군, 대구광역시 달성군, 울산광역시 울주군, 경기도 양평군, 강원도 홍천군, 경상북도 안동시를 대상으로 Table 7의 위험등급별 계약 및 손해상황 자료를 활용하였다. 여기서, 위험등급은 Table 1의 침수심(D)을 기준으로 하였다.
Table 7
Contract and Loss Situation by Risk Class
5.2 위험등급별 보험요율차등화의 타당성 검증
본 절에서는 Table 7에서 2008∼2014까지의 7개년간 손해율 데이터를 가지고 위험등급별 보험요율차등화의 타당성을 검증하였다. Table 8의 Kruskall-Wallis의 검정 결과와 검정통계량은 Won et al. (2013)을 활용하였다.
Table 8
Kruskall-Wallis’ Test Result and Test Statistic
따라서 근사 유의확률이 0.04로서 유의수준 0.05하에서 유의수준보다 근사 유의확률이 작으므로 귀무가설(H0)을 기각한다. 따라서 위험등급 간에 손해율의 차이가 있다고 판단되므로 합리적인 보험요율 차등화를 위해서는 현행 시⋅군⋅구별 단일요율을 위험등급별 보험요율로 전환해야만 지역별 위험도에 따른 합리적인 보험요율 차별화가 가능해질 수 있다.
5.3 위험등급별 신뢰도 및 손해율 추정
본 절에서는 Table 7의 2008∼2014까지의 7개년 간 계약 및 손해상황 데이터를 가지고 2015년도의 위험등급별 손해율을 추정하고 그 결과를 2015년도 실제 손해율과 비교⋅분석하였다.
5.3.1 변동제한법에 의한 위험등급별 신뢰도 및 손해율 추정
KIDI (2011)에 의한 손해율의 추정은 다음 Eq. (1)′과 같이 이루어진다.
Eq. (1)′에서 ｢① 가중치 반영 손해율｣은 다음과 같이 최근년도를 기준으로 가중치를 부여해서 산정하였다. 다만, KIDI (2011)에서는 통계기간을 5년과 10년을 기준으로 하고 있으나 본 사례분석에서는 통계기간이 7년이므로 Table 9와 같이 통계기간별 가중치를 수정하였다.
Table 9
Weighted Value by Statistical Period(From Recent Year) (Unit: %)
Eq. (1)′의 ｢② 부분신뢰도Zp｣ 산정은 Eqs. (4)와 (8)에 따라 다음 Eq. (16)과 같이 된다. 여기서n은 위험단위별 사고건수, y는 확률수준 P(95%)에 대응하는 표준화 값(1.96)이고k는 범위모수(0.1)이다. s와 x̄는 손해액의 표본표준편차와 표본평균을 말한다.
Eq. (1)′에서 ｢③ 신뢰도의 보수｣는 위험등급을 구분하지 않은 상위등급의 전체 평균손해율을 말한다. 이상과 같은 제 요인들을 반영한 위험등급별 신뢰도 Z i ( L F A ) X ^ i ( L F A ) Z i ( L F A ) X ^ 1 ( L F A ) n F = 384 × ( 1 + C V 2 ) = 384 × [ 1 + ( 7.98 9.58 ) 2 ] = 650 Z 1 ( L F A ) = 43 650 = 0.26
Table 10
Estimation of the Partial Credibility and Loss Ratio by Risk Class
| Risk Class |
Partial Credibility( |
Estimated Loss Ratio( |
|---|---|---|
| 1 | 0.26 | 15.25 |
| 2 | 0.08 | 15.90 |
| 3 | 0.09 | 18.03 |
| 4 | 0.10 | 27.30 |
동일한 방법에 의해 계산한 나머지 위험등급의 부분신뢰도와 추정손해율은 Table 10과 같다.
5.3.2 Bühlmann-Straub의 경험적 베이즈 신뢰도 및 손해율 추정
일반적인 위험단위수(Eit)를 가중치로 한 위험등급별 신뢰도와 추정 손해율은 Table 11과 같다. 예시적으로, 일반적인 위험단위수Eit를 보험료(Pit)로 하는 경우의 위험등급별 신뢰도와 손해율을 추정하면 다음과 같다. 먼저, 위험등급 내 분산의 기댓값의 추정치(∑ ^ 2 τ 2 ^ X 1. ¯
Table 11
Estimation of the Credibility and Loss Ratio Based on General Number of Risk Units by Step
동일한 계산식에 의해 X 2. ¯ = 12.15 X 3. ¯ = 46.88 X 4. ¯ = 128.27 ∑ ^ 2
다음으로 2단계의 위험등급 간 평균의 분산 값의 추정치(τ 2 ^ X .. ¯
또한 Eq. (11)′의 W = ∑ i = 1 K ∑ t = 1 T ( i ) E i t E .. ( X i t − X .. ¯ ) 2
따라서 2단계의 Eq. (11)′에 의한 위험등급 간 평균의 분산 값의 추정치(τ 2 ^
3단계의 Eq. (12)′에 의한 위험등급 1의 Bühlmann- Straub의 경험적 베이즈 신뢰도는 다음과 같이 계산된다.
동일한 방법에 의해 계산한 나머지 위험등급별 신뢰도는 Z 2 ( B S ) = 0.75 Z 3 ( B S ) = 0.58 Z 4 ( B S ) = 0.87 X .. ¯ ( Z i )
마지막 5단계의 Bühlmann-Straub의 경험적 베이즈 신뢰도를 반영한 위험등급 1의 추정손해율은 다음과 같이 계산된다.
동일한 방법에 의해 계산한 위험등급별 신뢰도 X ^ 2 ( B S ) = 21.60 X ^ 3 ( B S ) = 48.16 X ^ 4 ( B S ) = 118.12
5.4 적합도 검증
변동제한법과 Bühlmann-Straub의 경험적 베이즈 신뢰도를 각각 적용해서 추정한 손해율과 2015년도의 실제손해율을 기준으로 Eq. (17)에 의해 적합도를 검증하였다. 다시 말해, Q값이 적다는 것은 추정치와 실제치 간의 차이가 적다는 것을 말해준다. 여기서 X i . ^
적합도 검증결과 Table 12에서 보는 바와 같이Q값이 가장 적게 나타나는 보험료(Pit)를 가중치로 한 Bühlmann-Straub의 경험적 베이즈 신뢰도가 2015년도의 실제 손해율을 가장 잘 나타내고 있다. 따라서 앞으로 보험요율 검증의 기준이 되는 손해율을 추정함에 있어 변동제한법에 의한 신뢰도 보다는 Bühlmann-Straub의 경험적 베이즈 신뢰도를 활용하는 것이 보다 더 합리적이라는 사실이 확인되었다. 다만, 본 사례분석에서는 자료접근의 한계로 충분한 데이터를 확보하고 있지 못하다는 점이다. 따라서 보다 더 합리적인 손해율 추정방법을 도출하기 위해서는 충분한 데이터가 필요하다고 판단된다.
Table 12
Goodness of the Fit Test Result
6. 결론
풍수해보험은 ｢재난 및 안전관리 기본법｣에 따른 사유재산피해 지원제도를 대체하기 위해 도입된 정책보험으로 보험요율산정의 3원칙(공정성의 원칙, 충분성의 원칙, 비과도성의 원칙)이 적용되어야만 한다. 그러나 현행 풍수해보험 요율체계는 보험가입목적물이 위치하고 있는 지역의 위험도와 관계없이 하나의 시⋅군⋅구를 하나의 요율산정단위로 적용함으로써 ｢보험요율은 보험계약자의 위험도에 따라 부당하게 차별을 받지 않도록 공정해야 한다.｣는 공정성의 원칙에 어긋나고 있다. 따라서 공정성의 원칙이 적용되기 위해서는 현행과 같은 시⋅군⋅구별 단일요율체계를 본 연구에서 제안한 지역별 위험도가 반영된 위험등급별 보험요율체계로 전환하지 않으면 안된다. 또한 보험요율 검증의 기준이 되는 손해율을 추정함에 있어 변동제한법에 의한 신뢰도를 적용함으로써 보험요율산정가의 주관적 판단에 따라 추정 결과가 차이가 날 수 있다는 문제점이 제기되고 있다. 따라서 주관적 판단을 배제시킬 수 있는 새로운 형태의 신뢰도 추정방법의 도입이 필요하다.
이 같은 점들을 고려하여 본 연구에서는 하나의 시⋅군⋅구를 침수심에 따라 4개의 동질위험집단으로 나눔으로써 보험가입목적물이 위치하고 있는 지역별 위험도에 따라 합리적인 보험요율의 차별화가 이루어 질 수 있다는 점이 Kruskall-Wallis의 동질성 검증방법을 통해 확인되었다. 또한 Bühlmann-Straub의 경험적 베이즈 신뢰도를 이용하여 위험등급별 손해율을 추정함으로써 변동제한법의 단점으로 제기되는 주관적 판단을 배제시킬 수 있다는 것을 실증적 사례분석을 통해 확인하였다. 다만, 본 연구에서는 데이터 집적의 한계로 7개 시⋅군⋅구만을 대상으로 하였으나 향후 전국 232개 시⋅군⋅구의 경험데이터를 이용하여 손해율을 추정한다면 보다 더 신뢰성 있는 추정결과가 나올 것으로 판단된다. 향후 ｢풍수해보험 위험도가 반영된 개별보험요율 산정 및 지도개발(국민안전처)｣ 연구과제의 일환으로 추진 중에 있는 보험목적물별 DB가 구축된다면 본 연구에서 제시하고 있는 데이터 집적의 한계를 극복할 수 있을 것으로 기대된다.
PDF Links
PubReader
ePub Link
Full text via DOI
Download Citation
Print
