1. м„ң лЎ
2. м•Ҳм „м§„лӢЁ лҚ°мқҙн„° кө¬м¶•
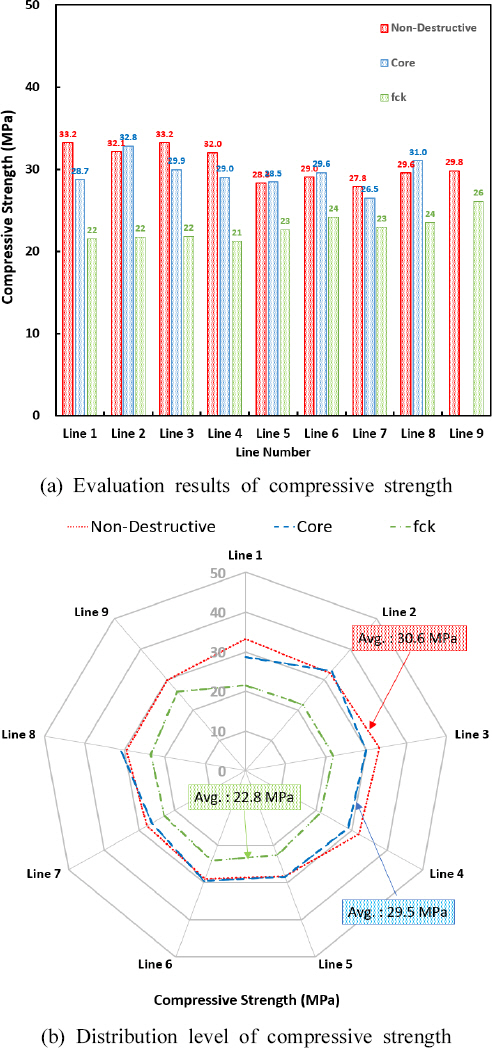
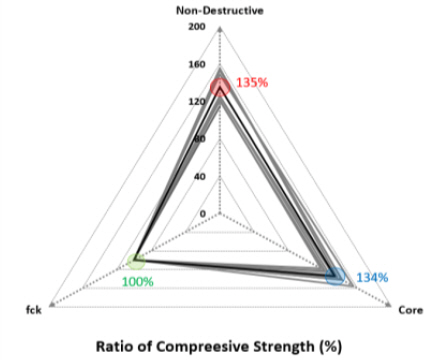
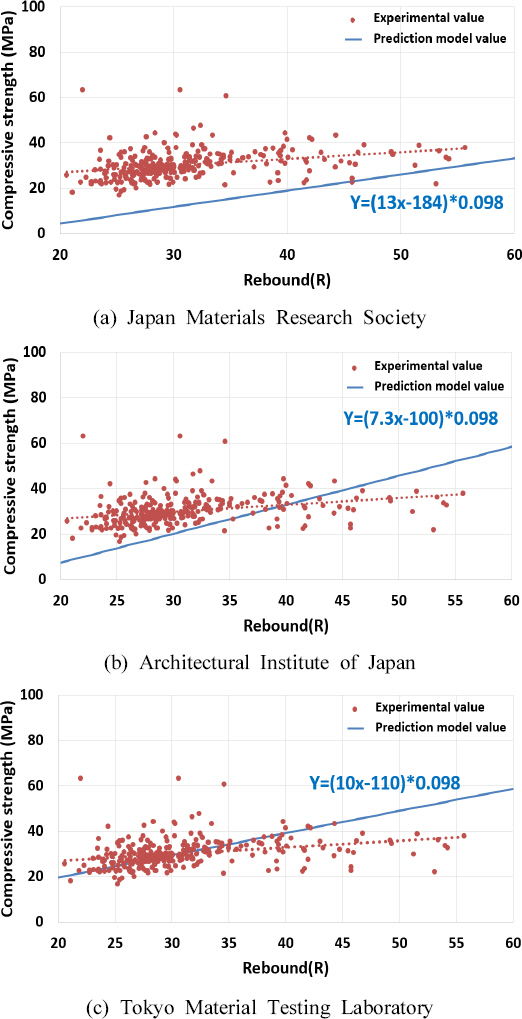
2.1 ліҙнҶөк°•лҸ„ мҪҳнҒ¬лҰ¬нҠё лҚ°мқҙн„° мҲҳ집 л°Ҹ кІ°кіј 분м„қ
2.2 кі к°•лҸ„ мҪҳнҒ¬лҰ¬нҠё лҚ°мқҙн„° мҲҳ집 л°Ҹ кІ°кіј 분м„қ
TableВ 1
| Type | Compressive Stength (EA) | PAB (8) | DGB (5) | FHB (3) | CCWB (3) | CWS (3) | ESW (3) | RWB (3) | |
|---|---|---|---|---|---|---|---|---|---|
| Reactor 1 | Non. Destructive | Rebound Value (s) | 59.9 (4.1) | 58.4 (1.9) | 60.3 (2.5) | 58.0 (2.4) | 60.7 (0.7) | 60.2 (0.3) | 58.2 (2.2) |
| Conversion* (MPa) | 60.4 (2.9) | 59.5 (1.4) | 60.7 (1.5) | 59.4 (1.5) | 61.2 (0.3) | 61.0 (0.1) | 59.5 (1.5) | ||
| Core (MPa) | 52.2 (8.6) | 42.9 (6.5) | 47.1 (17.1) | 44.2 (4.8) | 58.2 (5.1) | 50.8 (22.6) | 48.9 (12.0) | ||
| Reactor 2 | Non. Destructive | Rebound Value (s) | 59.0 (5.4) | 56.8 (1.5) | 61.0 (1.4) | 58.4 (3.3) | 58.2 (1.8) | 58.9 (2.2) | |
| Conversion* (MPa) | 59.6 (4.2) | 57.8 (1.2) | 61.5 (0.9) | 59.3 (3.2) | 59.1 (1.5) | 60.0 (1.9) | |||
| Core (MPa) | 47.8 (18.0) | 43.7 (15.7) | 45.3 (20.7) | 41.5 (2.5) | 47.3 (10.7) | 47.2 (10.4) | |||
TableВ 2
| Regression Analysis Statistics | |
|---|---|
| Multiple Correlation Coefficient | 0.321139 |
| R-squared | 0.103130 |
| Adjusted Coefficient of Determination | 0.087115 |
| Standard Error | 6.410707 |
| Number of Observations | 58 |
3. мқёкіөм§ҖлҠҘмқ„ нҷңмҡ©н•ң 압축강лҸ„ мҳҲмёЎ лӘЁлҚё м„Өкі„ л°Ҹ мӢ лў°м„ұ нҸүк°Җ
3.1 н•ҷмҠөлӘЁлҚё м„Өкі„
3.1.1 лҚ°мқҙн„° кө¬м„ұ
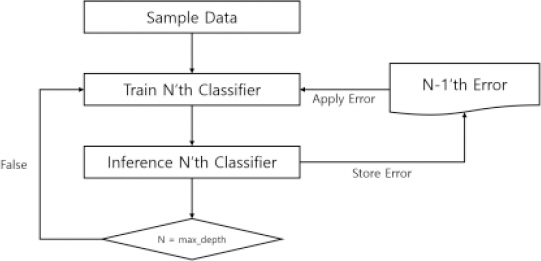
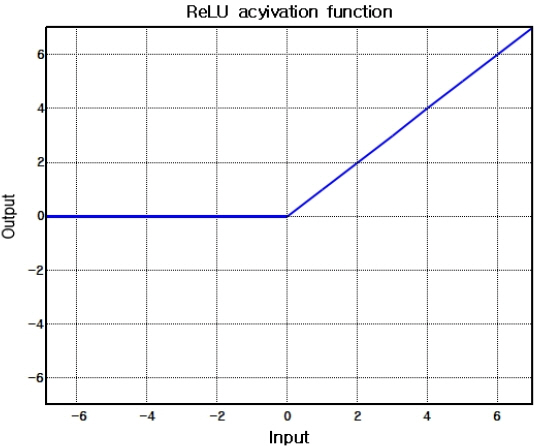
3.1.2 мқёкіөм§ҖлҠҘ лӘЁлҚё
3.2 н•ҷмҠөлӘЁлҚё мӢ лў°м„ұ нҸүк°Җ л°Ҹ 분м„қ
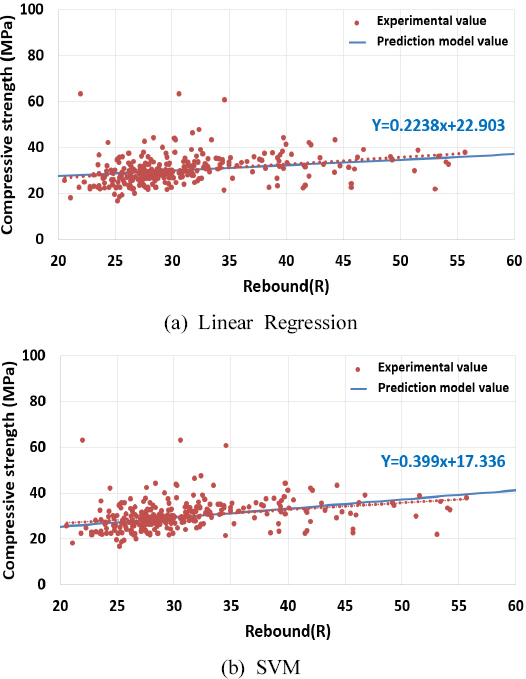
3.2.1 лӘЁлҚёнҸүк°Җ л°©лІ•
3.2.2 мӢ лў°м„ұ нҸүк°Җ
TableВ 5
TableВ 6
| Type | Linear Regression | SVM | XGBoost | Neural Network |
|---|---|---|---|---|
| MAE | 4.21 | 3.87 | 4.41 | 3.92 |
| MSE | 28.09 | 25.75 | 34.24 | 25.83 |
| RMSE | 5.30 | 5.08 | 5.85 | 5.08 |
| RMSLE | 0.17 | 0.16 | 0.19 | 0.16 |
4. кІ° лЎ
1) кө¬мЎ°л¬јнҶөн•©м •ліҙмӢңмҠӨн…ң(FMS) л°Ҹ м•Ҳм „м§„лӢЁмқ„ нҶөн•ҙ м–»м–ҙ진 ліҙнҶөк°•лҸ„ л°Ҹ кі к°•лҸ„ мҪҳнҒ¬лҰ¬нҠёмқҳ к°•лҸ„ лҚ°мқҙн„°лҘј мҲҳ집н•ҳкі л¶„м„қн•ң кІ°кіј, м§Җн•ҳ кө¬мЎ°л¬ј л°Ҹ мӣҗм „ кө¬мЎ°л¬јмқҖ лӘЁл‘җ 압축강лҸ„к°Җ м„Өкі„кё°мӨҖмқ„ мғҒнҡҢн•ҳлҠ” кІ°кіјлҘј ліҙмҳҖмңјл©°, кө¬мЎ°л¬јмқҳ м•Ҳм „м„ұм—җ л¬ём ңк°Җ м—ҶмқҢмқ„ нҷ•мқён• мҲҳ мһҲм—ҲлӢӨ.
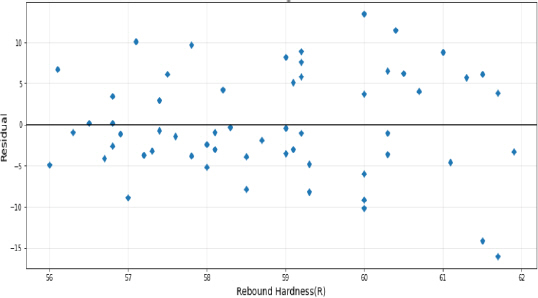
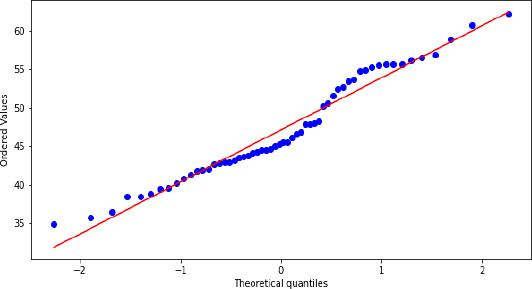
2) л°ҳл°ңкІҪлҸ„мҷҖ мҪ”м–ҙ 압축강лҸ„ к°„мқҳ нҶө계분м„қмқ„ мҲҳн–үн•ң кІ°кіј, л‘җ ліҖмҲҳ к°„мқҳ мғҒкҙҖкҙҖкі„лҠ” к°•н•ҳм§Җ м•Ҡм§Җл§Ң, лҚ°мқҙн„°мқҳ нҸүк· м°ЁлҠ” нҶөкі„м ҒмңјлЎң мң мқҳлҜё н•Ёмқ„ліҙм—¬мЈјмҳҖлӢӨ. мқҙлҠ” л°ҳл°ңкІҪлҸ„лҘј нҶөн•ҳм—¬ 압축강лҸ„лҘј мҳҲмёЎн•ҳлҠ” кІғмқҙ м •нҷ•нһҲ мқјм№ҳн•ҳм§ҖлҠ” м•Ҡм§Җл§Ң м–ҙлҠҗм •лҸ„мқҳ м—°кҙҖм„ұмқҙ мЎҙмһ¬н•ҳлҠ” кІғмңјлЎң нҢҗлӢЁлҗңлӢӨ.
3) мқёкіөм§ҖлҠҘ лӘЁлҚёмқҖ нҳ„н–ү к°•лҸ„ мҳҲмёЎ лӘЁлҚёкіј 비көҗн•ҳм—¬ мҳҲмёЎ мҳӨм°Ёк°Җ к°җмҶҢн•ҳлҠ” кІ°кіјлҘј м–»мқ„ мҲҳ мһҲм—Ҳмңјл©°, м—җлҹ¬мңЁ к°җмҶҢ л°Ҹ м •нҷ•лҸ„ н–ҘмғҒмңјлЎң мқён•ҳм—¬ мӢӨн—ҳк°’мқҳ нҡҢк·ҖкіЎм„ м—җ лҢҖн•ҳм—¬ м„ӨлӘ…н• мҲҳ мһҲлҠ” кІғмңјлЎң лӮҳнғҖлӮ¬лӢӨ.