1. м„ң лЎ
TableВ 1
2. м—°кө¬м§Җм—ӯ
3. л°©лІ•лЎ
3.1 кұҙл¬ј мҶҗмғҒм •лҸ„ 분м„қ
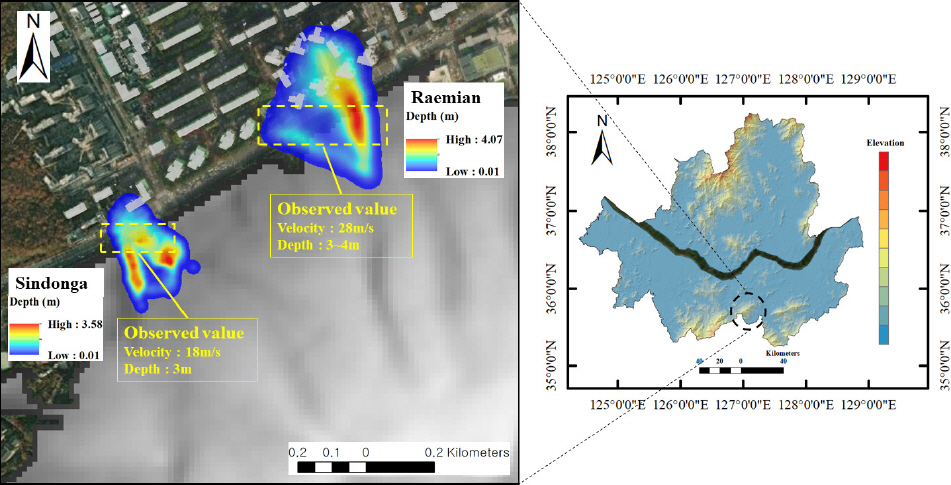
3.2 м—°кө¬м§Җм—ӯ м—ӯн•ҙм„қ
TableВ 2
TableВ 3
| Factor | Region | |||
|---|---|---|---|---|
| Raemian | Sindonga | |||
| Observed value | Estimated value | Observed value | Estimated value | |
| Velocity (m/s) | 28 | 25.7 | 18 | 17.5 |
| Height (m) | 3~4 | 4.07 | 2~3 | 2.8 |
3.3 мң„н—ҳк°•лҸ„ 분м„қ
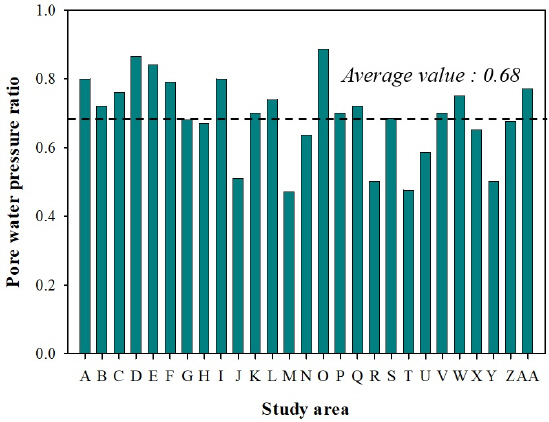
4. нҶ м„қлҘҳ л¬јлҰ¬м Ғ м·Ём•ҪкіЎм„
TableВ 4
| Hazard intensity | Building type | |
|---|---|---|
| RC-frame | Non-RC frame | |
| Impact pressure, Pt (kPa) | V=0.707(1вҲ’e(вҲ’0.0016Г—Pt1.5)) | V=1.012(1вҲ’e(вҲ’0.0358Г—Pt0.967)) |
5. кІ° лЎ
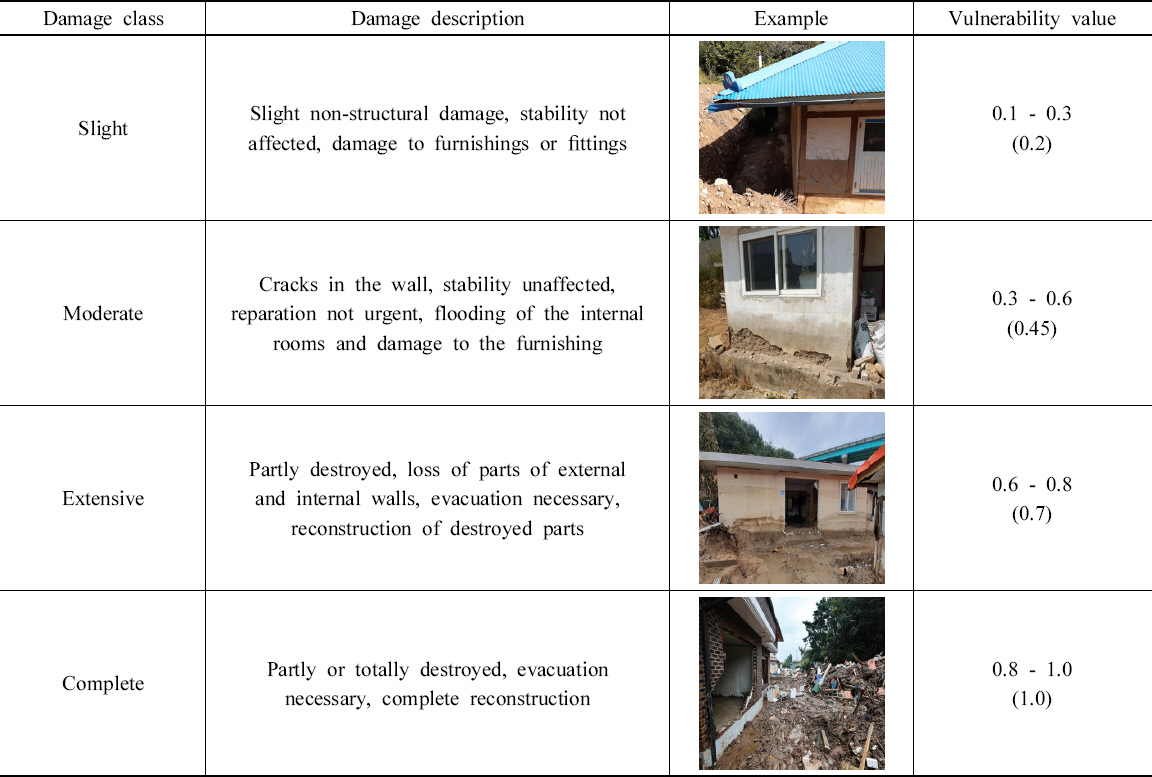
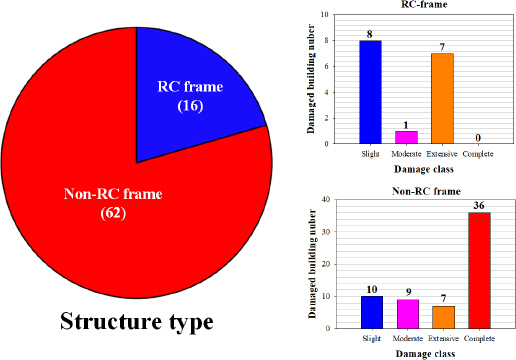
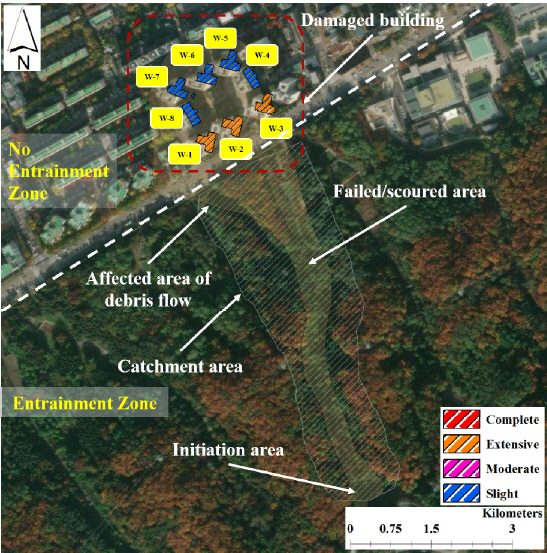
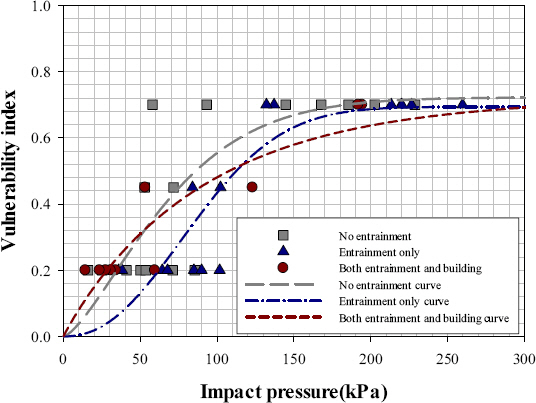
1) кұҙл¬јмқҳ мҶҗмғҒм •лҸ„лҘј 분м„қн•ҳкё° мң„н•ҙ нҶ м„қлҘҳм—җ мқҳн•ҙ н”јн•ҙл°ӣмқҖ кұҙл¬јмқ„ ліҙк°• мҪҳнҒ¬лҰ¬нҠё кө¬мЎ°(RC-frame)кіј 비ліҙк°• мҪҳнҒ¬лҰ¬нҠё кө¬мЎ°(Non-RC frame) мң нҳ•мңјлЎң 분лҘҳн•ҳмҳҖлӢӨ. к·ёлҰ¬кі м·Ём•Ҫм§ҖмҲҳ лІ”мң„м—җ л”°лқј Slight, Moderate, Extensive, CompleteлЎң 분лҘҳн•ҳмҳҖлӢӨ. ліҙк°• мҪҳнҒ¬лҰ¬нҠё кө¬мЎ°мқҳ н”јн•ҙкұҙл¬јмқҖ 16к°ңлЎң Slight 8к°ң, Moderate 1к°ң, Extensive 7к°ң, Complete 0к°ңлЎң 분м„қлҗҳм—Ҳкі , 비ліҙк°• мҪҳнҒ¬лҰ¬нҠё кө¬мЎ°мқҳ н”јн•ҙкұҙл¬јмқҖ 62к°ңлЎң Slight 10к°ң, Moderate 9к°ң, Extensive 7к°ң, Complete 36к°ңлЎң 분м„қлҗҳм—ҲлӢӨ. 비ліҙк°• мҪҳнҒ¬лҰ¬нҠё кө¬мЎ°лҠ” ліҙк°• мҪҳнҒ¬лҰ¬нҠё кө¬мЎ°ліҙлӢӨ к°•м„ұлҸ„к°Җ лӮ®кі , лҢҖл¶Җ분 мӮ°м§Җ кІҪкі„л¶ҖмҷҖ к·јм ‘н•ң кіім—җ мң„м№ҳн•ҳм—¬ мҶҗмғҒм •лҸ„к°Җ лҢҖл¶Җ분 мҷ„нҢҢмқё кІғмңјлЎң 분м„қлҗҳм—ҲлӢӨ.
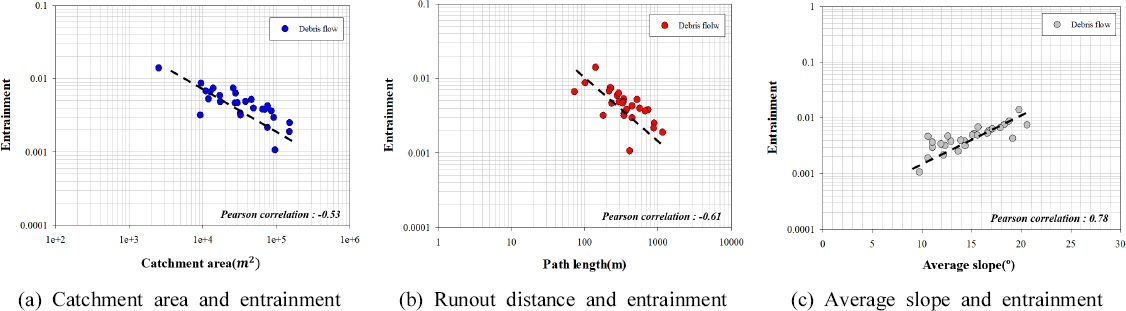
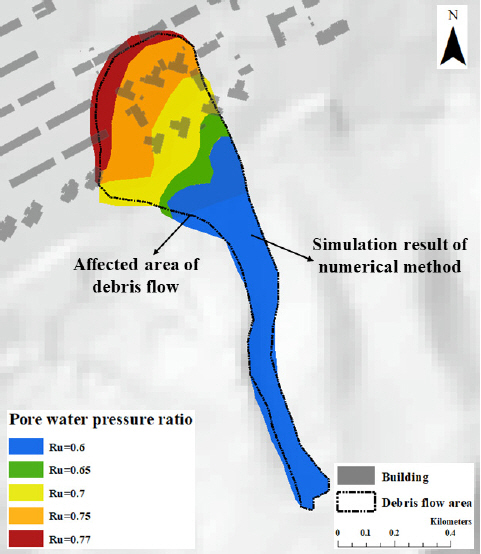
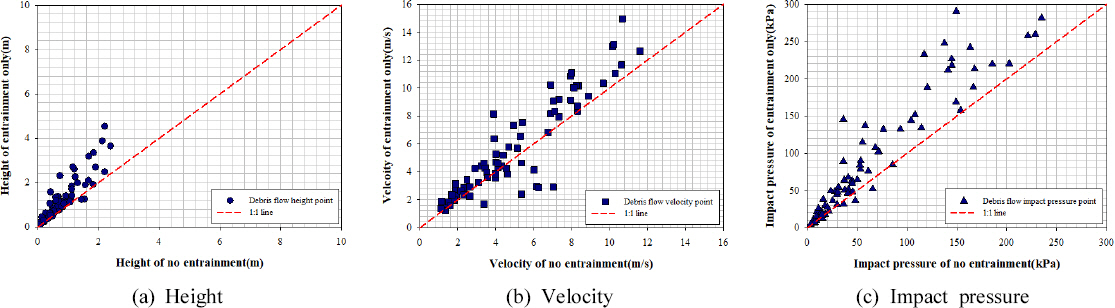
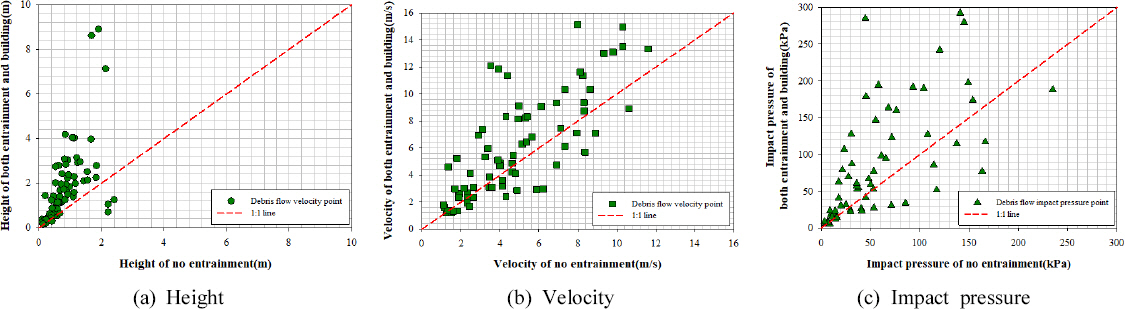
2) DAN3D н”„лЎңк·ёлһЁмқ„ нҶөн•ҙ м—°н–үмқ„ кі л Өн•ҳм§Җ м•Ҡм•ҳмқ„ л•Ң, м—°н–үмқ„ кі л Өн•ҳмҳҖмқ„ л•Ң, м—°н–үкіј кұҙл¬јмқ„ кі л Өн•ҳмҳҖмқ„ л•Ңмқҳ мң„н—ҳк°•лҸ„(мҶҚлҸ„, лҶ’мқҙ)лҘј мӮ°м •н•ҳм—¬ 충격압мқ„ мӮ°м •н•ҳмҳҖлӢӨ. к°Ғ кІҪмҡ°м—җ л”°лқј мӮ°м •лҗң мң„н—ҳк°•лҸ„лҘј 분м„қн•ң кІ°кіј м—°н–үкіј кұҙл¬јмқ„ кі л Өн•ҳм§Җ м•Ҡм•ҳмқ„ л•ҢмҷҖ м—°н–үл§Ң кі л Өн•ҳмҳҖмқ„ л•ҢлҠ” м·Ём•Ҫм§ҖмҲҳк°Җ лӮ®мқҖ кұҙл¬јм—җм„ңлҸ„ лҶ’мқҖ мң„н—ҳк°•лҸ„к°Җ 분м„қлҗҳм—Ҳм§Җл§Ң м—°н–үкіј кұҙл¬јмқ„ лҸҷмӢңм—җ кі л Өн•ҳмҳҖмқ„ л•ҢлҠ” нҶ м„қлҘҳ мҳҒн–Ҙмқ„ м§Ғм ‘ л°ӣлҠ” м•һ кұҙл¬јм—җм„ң нҮҙм Ғ лҶ’мқҙлҠ” мҰқк°Җн•ҳмҳҖкі , нҶ мӮ¬ нҮҙм Ғмқҙ мў…лЈҢлҗҳлҠ” л’ӨмӘҪ кұҙл¬јм—җм„ң нҮҙм Ғ лҶ’мқҙмҷҖ мҶҚлҸ„лҠ” к°җмҶҢн•ҳлҠ” кІғмқ„ м•Ң мҲҳ мһҲм—ҲлӢӨ.
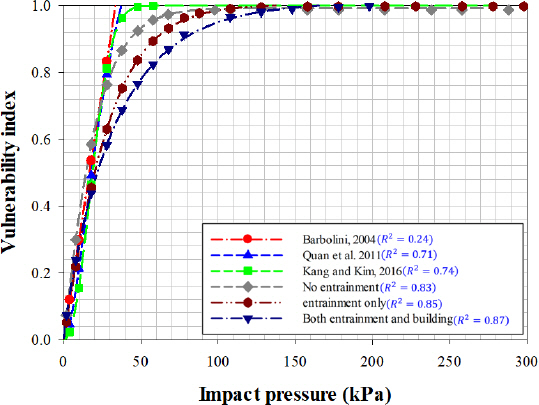
3) кұҙл¬ј мҶҗмғҒм •лҸ„мҷҖ нҶ м„қлҘҳ 충격압 кҙҖкі„лҘј мӢңк·ёлӘЁмқҙл“ң н•ЁмҲҳлҘј м Ғмҡ©н•ҳм—¬ л№„м„ нҳ• нҡҢк·Җ분м„қмқ„ нҶөн•ҙ нҶ м„қлҘҳ м·Ём•ҪкіЎм„ мқ„ лҸ„м¶ңн•ҳмҳҖлӢӨ. ліҙк°• мҪҳнҒ¬лҰ¬нҠё кө¬мЎ°мҷҖ 비көҗн•ҳл©ҙ 비ліҙк°• мҪҳнҒ¬лҰ¬нҠё кө¬мЎ°м—җм„ң мһ‘мқҖ 충격압м—җм„ңлҸ„ м·Ём•Ҫм§ҖмҲҳк°Җ л№ лҘҙкІҢ 1м—җ мҲҳл ҙн•ҳлҠ” нҳ•нғңмқҳ нҢЁн„ҙмқ„ ліҙмҳҖкі , лӮ®мқҖ мң„н—ҳк°•лҸ„м—җм„ң нҒ° кұҙл¬ј мҶҗмғҒмқҙ л°ңмғқн• мҲҳ мһҲлҠ” кІғмқ„ м•Ң мҲҳ мһҲм—ҲлӢӨ. лҳҗн•ң кё°мЎҙ м„ н–үм—°кө¬мҷҖ кІ°м •кі„мҲҳлҘј 비көҗ 분м„қн•ң кІ°кіј м—°н–үкіј кұҙл¬јмқ„ кі л Өн•ҳмҳҖмқ„ л•Ңмқҳ кІ°м •кі„мҲҳк°Җ к°ҖмһҘ лҶ’мқҖ кІғмңјлЎң 분м„қлҗҳм—ҲлӢӨ. нҶ м„қлҘҳ м·Ём•ҪкіЎм„ кіј м·Ём•Ҫн•ЁмҲҳлҠ” нҶ мӮ¬мһ¬н•ҙ мң„н—ҳм§Җм—ӯмқҳ кұҙл¬ј мҶҗмғҒм •лҸ„лҘј нҢҢм•…н• л•Ң мқҙмҡ©н• мҲҳ мһҲкі , нҶ мӮ¬мһ¬н•ҙ м·Ём•Ҫм„ұ нҸүк°ҖлҘј мң„н•ң кё°мҙҲмһҗлЈҢлЎң нҷңмҡ©лҗ мҲҳ мһҲмқ„ кІғмңјлЎң кё°лҢҖлҗңлӢӨ.