Key Parameters and Input Variables for the Reduction of Uncertainty using Modified Pedigree Matrix

건희 정; 규범 심; 응석 김

doi:10.9798/KOSHAM.2016.16.1.329

Abstract

Due to the rapidly increased urbanization and climate change, impervious area becomes smaller and torrential rainfall is occurred frequently. These caused severe urban flood with severe property damages and human lives. To cope with the urban flood, pumping stations with retention/detention ponds have been constructed. Therefore, the pumping stations have to be included in the urban flooding system or rainfall-runoff systems for the accurate analysis, the uncertainty incurred by the rainfall-runoff models or input data and/or parameters caused difficulties. In this study, modified Pedigree matrix is proposed based on the original Pedigree matrix and input data and parameters which might cause the uncertainty in the systems are selected. The contribution is analyzed with the modified Pedigree matrix and uncertainty index. As a result, basin width and roughness of pervious and impervious areas have the highest contribution to the uncertainty and the more accurate estimation is required. The proposed results could be applied in the pumping station operations in the urban area.

Keywords: Drainage pumping station, Uncertainty, SWMM model, Modified Pedigree matrix

요지

최근 급격히 증가되고 있는 도시화로 인해 불투수지역의 비율이 감소되고 있으며, 이상기후로 인한 집중호우 및 게릴라성 폭우가 빈번히 발생하고 있다. 이러한 이유로 내수침수 및 인명피해, 막대한 재산피해를 가져오고 있으며, 피해를 방지하기 위해 빗물펌프장 등이 설치되고 있다. 그러므로 도시홍수 분석 및 도시유역에서의 유출해석을 위해서는 빗물펌프장을 고려하여 분석하는 것이 필수적이지만, 유출모형 및 빗물펌프장 운영자료들이 불확실성을 가지고 있어 정확한 모형 해석 및 분석에 어려움이 있다. 따라서 본 연구에서는 자료의 품질평가에 사용되는 Pedigree matrix를 수정하여 수정 Pedigree matrix를 제안하고, 이를 이용한 빗물펌프장을 포함한 도시유역의 유출해석에서 불확실성을 야기할 것으로 예상되는 자료 및 매개변수를 선정하였다. 선정된 자료들을 대상으로 Pedigree matrix 점수와 불확실성 지수를 이용한 불확실성에 대한 기여도를 평가한 결과, 유역폭, 투수 및 불투수유역의 조도계수가 가장 불확실성이 높게 나타나 정확한 매개변수 추정이 필요하다는 결론을 내릴 수 있었다. 이 결과는 도시유역의 유출 해석 및 빗물펌프장 운영 시 중요매개변수 선정에 도움을 주리라 판단된다.

1. 서론

최근 발생하는 도시유역의 홍수피해는 내수에 의한 침수로 분석되고 있으며, 집중호우 및 게릴라성 폭우로 인한 침수의 피해는 대부분 내수배제의 불량인 것으로 나타났다. 내수에 의한 침수는 인명 피해 및 재산피해를 가져오며, 이러한 피해를 막기 위해 정확한 강우-유출 해석이 필요하지만 실제 자연을 해석하는데 모형의 오차가 발생한다. 또한 모형 입력변수들이 불확실성을 가지고 있어 정확한 모의를 하는데 어려움이 있으며, 이는 모형 결과값의 신뢰성에 영향을 미치게 된다. 따라서 매개변수의 불확실성을 예측하여 유출해석에 반영하고, 각 입력자료가 가지는 중요도 정도를 파악한다면 내수 침수를 예방하는데 큰 기여를 할 것으로 판단된다.

불확실성을 고려한 불확실성 매개변수를 선정하기 위해서는 기여도 분석이 필요하다. 이에 따른 문헌조사를 살펴보면 Park and Oh(2012)은 하천 유량조건에 따른 목표수질 초과현상을 정량화하여 분석할 수 있도록 목표수질 초과지역에 대한 유황별 목표수질 초과율 및 초과기여도를 분석하였으며 Woo et al.(2010)은 한강상류수계에 위치한 환경기초 시설들이 직접 방류되는 본류 유입지점 및 팔당호 유입지점의 인 수질농도에 미치는 인 기여도를 분석하고 인 기준농도 강화에 따른 환경 기초시설의 인 부하량 삭감시 수질개선기여도를 분석하였다. Choi et al.(2009)은 지리정보체계(GIS)의 격자기반 GIUH 모형을 이용하여 배수경로의 이질성에 따른 지표면 유동과 하천망 유동의 상대적 기여도를 정량적으로 평가하였으며 Kim et al.(2006)은 유역규모의 응답과정에 대한 지표면유동과 하천유동의 상대적 기여도를 평가하였다. Kim and Kim(2010)은 SWAT-K 모형의 적용을 통해 신뢰성 있는 장기간의 유량 및 수질모의자료를 기반으로 오염물질의 거동특성을 파악하기 위해 소유역 하천구간별 유달율을 산정하고, 점·비점오염원, 토지이용별 기여도를 산정하였다. Moon et al.(2010) 하수종말처리시설에서 하천으로 방류되는 물의 양이 하천유량에서 차지하는 비중을 파악하기 위해 홍수기(6~9월)를 제외한 기간에 대해 하천유량과 하수종말처리시설의 방류수량을 검토하여 하수처리수의 기여도를 분석하였다.

도시지역의 유출해석시 많이 사용되는 모형은 SWMM이다. EPA-SWMM에 사용되는 매개변수는 약 40개정도 되며, 유출해석시 약 10개 정도의 매개변수를 주요 매개변수로 볼 수있다(Chung et al., 2015). 모형에 입력되는 매개변수는 유출해석에 크거나 작은 영향을 미치게 되며 매개변수 선정에 관한 문헌조사를 살펴보면 다음과 같다. Joo and Park(2013)은 강우-유출모형 모의를 통하여 산정된 유출량 값의 신뢰도에 영향을 미치기 때문에 모형 입력자료들이 가지는 불확실성 정도를 정량화한 후 민감도 분석 및 불확실성 분석을 통한 매개변수 우선순위를 정하였다. Ning Sun et al.(2013)은 SWMM모형의 불확실성 평가를 위해 GLUE를 이용하여 분석 하였다. Sharifan et al.(2010)은 SWMM 모형을 이용하여 맨홀 수심의 계산과 소유역의 첨두홍수량의 불확실성을 민감도 분석하였다. Koo(2005)은 군자배수구역에서 실측된 유출 및 수질자료를 사용하여 주요 수질해석 모형 PC-SWMM에 대해 GA를 통한 유출, 수질 주요매개변수의 최적화와 민감도 분석을 하여 모형의 적용성 향상에 기여하였다. Kwon et al.(2013)은 HEC-1 단일강우사상 모형과 연동할 수 있는 Bayesian Markov Chain Monte Carlo(MCMC) 기반의 Bayesian HEC-1(BHEC-1) 통합 모델을 개발하였다. 개발된 모형을 이용하여 안정된 매개변수를 추정하였으며 강우-유출 모형 매개변수의 불확실성을 정량화 하여 불확실성을 효과적으로 파악하였다. Park(2009)는 정확하고 안정적인 설계를 통하여 도시유출의 신뢰도를 높이고 위험도를 줄이며, 최적화된 경제적인 설계를 위하여 확률적인 이론을 적용한 불확실성과 위험도를 평가하였다. Yu et al.(2011)은 강우-유출 및 강우-유사유출 모의가 가능한 분포형 강우-유사-유출 모형을 선택하고 직접산정이 불가능하거나 불확실성을 포함한 유출관련 매개변수 및 유사유출관련 매개변수를 선정하였다. Kim et al.(1995)은 수공구조물의 설계와 평가에서는 불확실성이 항상 포함되기 때문에 이에 따른 위험도의 산정이 반드시 필요하다. 따라서 서울시의 58개 배수구역의 우수관거에 대하여 신뢰도 분석기법을 적용하고, 이에 따른 위험도를 산정하여, 위험도와 안전율과의 관계를 유도, 우수관거의 설계와 평가시 이를 활용할 수 있는 기법을 제시하였다. Jung et al.(2013)은 홍수범람도 구축에서 발생할 수 있는 불확실성 요소들 가운데 조도계수 외에, 수위-유량관계식에서 발생하는 불확실성까지 고려하여 홍수범람도에 미치는 영향을 GLUE를 이용하여 산정하였다.

종합적인 검토결과 도시지역내 강우-유출해석 및 빗물펌프장의 불확실성을 고려한 매개변수 선정에 관한 기존 연구는 민감도 분석 등을 통하여 민감도가 높은 매개변수를 주요한 매개변수로 선정하였다. 따라서 본 연구에서는 강우-유출해석모형 및 빗물펌프장 관련 불확실성 매개변수를 선정하고 데이터 품질 평가에 사용되는 Pedigree matrix를 본 연구에 맞게 수정 Pedigree matrix를 제안하였다. 또한, 제안된 수정 Pedigree matrix와 정량화된 불확실성 지수를 이용하여 모형 및 빗물펌프장 주요 매개변수를 선정하였다.

2. 연구방법

2.1 불확실성을 유발하는 인자 선정

도시유역의 유출계산에 사용되는 자주 사용되는 EPASWMM의 매개변수를 대상으로 불확실성을 유발할 가능성이 있는 매개변수들을 선정하였다. EPA-SWMM에는 많은 수의매개변수가 있으나, 물리적으로 의미를 가지며 결과에 영향을 미치는 것으로 알려져 있는 매개변수들을 기존의 문헌과 연구를 참고하여 선정하였다. 또한 내수침수가 주로 발생하는 도시지역에 건설되어 운영되고 있는 빗물펌프장의 홍수방어대책으로서의 중요성을 고려하기 위한 인자들을 선정하였다. 현재 국내에 건설되어 운영되고 있는 빗물펌프장은 대체로 유수지를 함께 가지고 있어 유수지의 수위(내수위)에 따라 펌프의 가동시점이 결정된다. 또한 우수관을 통해 유수지로 유입된 유역유출량을 배출하는 외부 하천의 수위(외수위)도 관측하여한다. 그러므로 Table 1과 같은 매개변수 및 인자들을 선정하여 불확실성 분석을 시도하였다.

Table 1

Uncertainty Induction Parameters Select

SWMM Parameters	Drainage pump station parameter
▪ Basin width(m) ▪ Percentage of Impervious Area(%) ▪ Roughness of pervious area ▪ Roughness of impervious area ▪ CN ▪ Pipe roughness	▪ Inside water level(m) ▪ External water level(m) ▪ Pump output(m³/min) ▪ Rainfall(mm)

2.2 Pedigree Matrix를 이용한 자료의 품질평가

Pedigree matrix는 자료의 품질을 평가하기 위한 정성적인 방법으로 Weidema and Wesnæs(1996)가 제안한 데이터 품질지수(Data Quality Indicator, DQI) 중 하나이다. Pedigree matrix 기법은 기준이 분명하고 적용하기 쉬우며 알아보기가 편하다는 장점이 있다. 데이터 품질평가 기준은 신뢰성(Reliability), 완전성(Completeness), 시간상관성(Temporal correlation), 지역상관성(Geographical correlation), 기술상관성(Further technological correlation) 이상 5가지로 구성되어있다.

신뢰성은 데이터 출처, 획득방법 및 획득에 사용된 검증 절차를 평가한다. 완전성은 데이터의 통계적 특성과 관련한다. 얼마나 대표성 있는 샘플인지, 수집 데이터가 모집단의 특성을 잘 반영하고 있는지 그리고 데이터 수집기간이 적절한지를 평가한다. 시간상관성은 데이터 품질요건에서 정의한 대상년도와 수집데이터 사이의 시간적 관계를 평가한다. 지역상관성은 데이터 품질요건에서 정의된 대상지역과 수집된 데이터와의 관계를 평가한다. 기술상관성은 연구대상 기업, 공정 및 물질 데이터와 수집된 데이터와의 상관성을 평가한다. Table 2는 일반적으로 사용되는 Pedigree matrix에 대한 데이터 품질지수 및 세부 평가항목을 나타내었다. 각 세부 평가항목에 대한 점수를 1에서 5로 나타낸다.

Table 2

Pedigree matrix Data Quality Evaluation Standard

Division	Index Score	The detailed evaluation criteria
Reliability	1	Verified data based on measurements
	2	Verified data partly based on assumptions or non-Verified data based on
	3	Non-Verified data partly based on qualified estimates
	4	Qualified estimate
	5	Non-qualified estimate
Completeness	1	Representative data from all sites relevant for the market considered, over and adequate period to even out normal fluctuations
	2	Representative data from > 50% of the sites relevant for the market considered, over and adequate period to even out normal fluctuations
	3	Representative data from only some sites(<<50%) relevant for the market considered or >50% of sites but from shorter periods
	4	Representative data from only one site relevant for the market considered or some sites but from shorter periods
	5	Representativeness unknown or data from a small number of sites and from shorter periods
Temporal correlation	1	Less than 3 years of difference to the time period of the data set
	2	Less than 6 years of difference to the time period of the data set
	3	Less than 10 years of difference to the time period of the data set
	4	Less than 15 years of difference to the time period of the data set
	5	Age of data unknown or more than 15 years of difference to the time period of the data set
Geographical correlation	1	Data from area understudy
	2	Average data from larger area in which the area under study in included
	3	Data from area with similar production conditions
	4	Data from area with slightly similar production conditions
	5	Data from unknown or distinctly different area(North America instead of Middle East, OECD-Europe instead of Russia)
Further technological correlation	1	Data from enterprises, processes and materials under study
	2	Data from processes and materials under study but from different
	3	Data from processes and materials under study but from different technology
	4	Data on related processes or materials
	5	Data on related processes on laboratory scale or from different technology

일반적인 Pedigree matrix를 응용하여 Rousseaux and Suh(2001)는 전과정영향평가(Life-Cycle Assessment, LCA)를 위한 새로운 지수를 판단하는 기준을 다음 Table 3과 같이 제안하였다. 이 연구는 데이터 수집방법에 관하여 4가지 평가기준(Quality Indicator)을 토대로 하였다. 평가기준은 데이터 타당성(Justness), 완전성(Completeness), 대표성(Representative), 재현성(Representative), 불확실성(Uncertainty)으로 구분된다.

Table 3

Data Quality Assessment Criteria with a Pedigree matrix

Level	Quality indicator	Quality components
Flow	Justness	Statistical representativity of data
		Age of data
		Method of data acquisition
Process	Completeness	Exhaustiveness of identified flow
		Aggregation of flows
		Mass balance equibrium
Process	Representative	Geographical
		Time-related
		Technology
System	Representative	Rule of process inclusion/exclusion
		Rule of flow inclusion/exclusion
		Rule of functional unit definition
		Rule of allocation
Flow/system	Uncertainty	Data variability (propagation on the system)

응용된 Pedigree matrix에서는 타당성은 flow만을 평가하는데 적용되고, 공정(process)는 완전성과 대표성만을 평가한다. 또한 flow와 system의 불확실성도 평가하도록 제안하였다. 이 품질지수는 Pedigree matrix와 동일하게 1에서 5까지의 점수로 정량화된다.

2.3 수정 Pedigree Matrix를 이용한 자료의 기여도 평가

앞에서 선정한 불확실성 유발 인자 10개를 이용하여 Pedigree matrix 분석을 시도하였다. 일반적인 Pedigree matrix를 본 연구의 목적에 맞도록 수정하여 Table 4와 같이 제시하였다. 평가를 위한 기준을 크게 신뢰도, 지역상관성, 시간변이성, 외부영향성, 완전성 등 5개로 구분하고, 각 평가기준 별 1에서 4까지 점수로 평가하도록 하였다.

Table 4

Modification Pedigree matrix Assessment Standard

Division	Index Score	The detailed evaluation criteria
Reliability	1	The actual measured parameter value
	2	Parameters value by calculation
	3	Parameter values suggested by past experiments and measurements
	4	The assumed parameter values
Area Correlation	1	The parameter value of the target watershed
	2	Parameter value containing the target watershed
	3	Similar to the value of the target watershed basin
	4	The assumed parameter values
Time Variability	1	Unchanging of parameter value in accordance with basin and time change
	2	Change of parameter value in accordance with basin change
	3	Change of parameter value in accordance with time change
	4	Change of parameter value in accordance with basin and time change
External Impact	1	Unchanging parameter in accordance with mechanical and manager error
	2	Unchanging parameter in accordance with data and Data usage calculation expression
	3	Change of parameter in accordance with data and Data usage calculation expression
	4	Change of parameter in accordance with mechanical and manager error
Completeness	1	Sensitivity small representative data about the results
	2	Sensitivity big representative data about the results
	3	Can not know small sensitivity representative about result or incomplete data
	4	Can not know big sensitivity representative about result or incomplete data

신뢰성은 각 인자들이 실측값인지 일반화된 계산식에 의해 얻어진 값인지, 경험에 의해 가정된 값인지에 따라 다른 점수를 부여하도록 하였다. 직접 측정한 값인 경우의 신뢰성이 가장 높고, 가정된 값의 신뢰성이 가장 낮아 4점으로 기록하였으며, 이는 신뢰성에 의한 불확실성이 가장 크다는 것을 의미한다. 지역상관성은 대상 인자들이 해당 유역의 자료를 적용하여 결정된 값인가에 따라 다른 점수를 부여한다. 해당 유역과 직접적인 관련이 많을수록 작은 점수를 부여하여 지역상관성에 따른 불확실성이 작아진다. 시간변이성은 대상 인자들이 시간이 흐름에 따라 변할 가능성이 있는지 여부에 따라 점수를 부여하도록 하였다. 외부영향성은 매개변수 불확실성 정도의 영향을 평가기준에 의해 점수를 부여하는 지표 이다. 매개변수의 경우 기계적 오차 및 관리자의 능력에 따라 오차가 발생할 수 있으며, 데이터 사용에 따라 매개변수의 값이 변화하기 때문에 이에 따른 영향성을 파악하는 것은 중요하다고 판단된다. 완전성이란 선정된 매개변수가 측정 장소 및 측정방법이 합리적으로 해당 유역의 대표성을 가지는 지, 또는 유출해석시 사용된 강우사상과의 오차가 허용 오차 범위이내에 속하는지 등을 파악하여 해당 유역의 대표 데이터인지를 점수를 부여하는 지표이다. 본 연구에서 적용하기 위해 수정한 Pedigree matrix는 Table 4에 나타내었다.

2.3 불확실성 지수 산정

유역폭, 불투수면적비율, 투수 및 불투수유역의 조도계수, CN, 관 조도계수의 경우 유역의 특성을 반영한 매개변수이며 Chung et al. (2015) 연구의 매개변수 불확실성지수를 이용하였다. 불확실성 지수 공식에 대한 자세한 내용은 Chung et al.(2015)에 기술되어 있다. 기존의 매개변수 불확실성 산정공식은 Qais(1985)가 제시한 SWMM모형 매개변수의 불확실성지수 산정공식이며 식 (1)과 같이 나타내었다.

(1)

TU=∑i=1n1∑j=1n2(Yijm−Yi)2n1⋅n2

여기서, Yijm은 소유역 i의 j번째 모의발생 값, Y_i는 소유역 i의 모의발생된 총 n₂개의 평균값, n₁은 소유역의 개수이다.

3. 적용 및 결과

3.1 대상지역 및 SWMM 구축

본 연구의 대상지역인 가산1 빗물펌프장 유역은 서울시 금천구 가산동에 위치하고 있으며 0.48 km²의 유역면적을 차지하고 있다. 또한, 전체유역면적 중 공업지역이 73%로 대부분을 차지하고 있고, 기타 상업지역 등이 27%를 차지하는 대표적인 공업지역이다. 가산1 빗물펌프장 유역도를 Fig. 1(a)와 같이 나타내었다. 가산1 빗물펌프장 SWMM 모형 관망도는 Fig. 1(b)와 같으며, 총 절점 개수는 유출구를 포함하여 34개, 관로는 33개로 이루어져 있다.

Fig. 1

Location and Stormwater Pipe Network of Study Catchment.

3.2 불확실성 지수 산정

본 연구에서 불확실성 지수를 산정하기 위해 식 (1)을 이용하여 선정된 매개변수 10개에 대한 불확실성 지수를 산정하였으며 2012년 7월 6일~2012년 9월 5일의 일자별 빗물펌프장 운영자료를 사용하였다. 빗물펌프장 운영자료는 강우가 발생했을 때의 측정된 외수 및 내수, 토출량 자료를 이용하였다. 모형에서의 불확실성 매개변수인 유역폭, 불투수면적 비율, 투수 및 불투수유역의 조도계수, CN, 관 조도계수의 경우 모형 해석시 검·보정된 매개변수 값이 제안된다. 제안된 매개변수 값에 95%신뢰구간을 설정한 후 Monte Carlo Simulation을 통해 100개의 시나리오를 작성하였으며 식 (1)에 적용하여 불확실성 지수를 산정하였다. 그러나 빗물펌프장 관련 매개변수인 내수위, 외수위, 펌프토출량, 강우량의 경우 시간에 따라 매개변수의 값이 측정되어 변화하기 때문에 운영된 자료시간별 95% 신뢰구간을 설정한 후 모형에서의 불확실성 매개변수 불확실성 산정방법과 동일하게 100개의 시나리오를 작성하였다. 작성된 100개의 시나리오의 표준편차를 산정한 후 산정된 표준편차를 평균하여 각 일자별 불확실성 지수를 산정하였으며 산정된 일자별 불확실성 지수를 일별로 다시 평균하여 최종 불확실성 지수를 산정하였다.

불확실성 지수를 산정한 결과 Table 5와 같이 나타냈으며CN의 불확실성 지수가 0.097로 가장 높은 불확실성 지수로 나타났다. 또한, 불투수면적비율 및 불투수유역의 조도계수의 불확실성 지수가 0.094, 0.093으로 비슷한 불확실성 지수를 보였다. 그 다음으로 관 조도계수의 불확실성 지수가 0.085, 외수위 0.083, 투수유역의 조도계수 0.082, 유역폭 및 펌프 토출량 0.080, 내수위 0.032, 마지막으로 강우량의 불확실성 지수가 0.020으로 나타났다.

Table 5

Uncertainty Index Calculation Results

Parameter	Uncertainty Index	Parameter	Uncertainty Index
Basin width(m)	0.080	Pipe roughness	0.085
Percentage of Impervious Area(%)	0.094	Inside water level(m)	0.032
Roughness of impervious area	0.093	External water level(m)	0.083
Roughness of pervious area	0.082	Pump output(m³/min)	0.080
CN	0.097	Rainfall(mm)	0.020

3.3 수정 Pedigree Matrix를 이용한 평가

본 연구에서는 수정된 Pedigree matrix 기법을 이용하여 최종적인 점수를 산정하였다. Table 4의 각 매개변수별 총 5가지 지표의 세부평가 기준을 바탕으로 점수를 부여하였으며 5가지 지표 점수를 합산하여 최종적인 점수를 산정하였다. 최종적인 지표 점수의 합이 낮을수록 정확한 데이터 값을 의미하여 이와 반대로 점수가 커질수록 불확실성이 크다는 의미이다. 각 매개변수의 지표별 점수를 부여하여 최종적인 점수를 Table 6과 같이 나타내었다.

Table 6

Uncertainty Factor Evaluation Result using Pedigree matrix

Indicator score	Reliability	Area Correlation	Time Variability	External Impact	Completeness	Total
Basin width(m)	4	1	1	3	4	13
Percentage of Impervious Area(%)	2	1	2	3	1	9
Roughness of impervious area	4	1	2	3	4	14
Roughness of pervious area	4	1	2	3	4	14
CN	2	1	2	3	2	10
Pipe roughness	3	1	3	3	2	12
Inside water level(m)	1	1	1	4	1	8
External water level(m)	1	1	1	4	1	8
Pump output(m³/min)	1	1	1	4	3	10
Rainfall(mm)	1	2	1	4	1	9

각 항목별 점수를 부여한 기준은 연구자의 판단으로 결정하였다. 신뢰성은 각 자료들이 계산으로 구해진 값인지 가정된 값인지에 따라 점수를 결정하므로, 자료의 품질이 가장 좋다고 생각되는 측정값들에 1점을, 유역의 조도계수와 같이 가정한 값에 4점을 부여하였다.

고려된 자료와 매개변수들은 모두 같은 지역에서 수집된 것들이므로 강우량은 제외하고는 모두 1로 지정되었으며, 강우량은 지점강우량을 티센망을 이용하여 면적강우량으로 환산해야 하므로 2점을 부여하였다.

시간변이성은 자료 및 매개변수들이 시간적으로 상관성을 가지고 있는지 여부에 따라 결정하였고, 외부영향성은 측정의 오차가 클 수 있는 자료들에 큰 점수를 부여하였다. 마지막으로 완전성은 유역의 대표성을 가진다고 생각되는 자료에 작은 점수를 대표성이 떨어진다고 생각되는 자료에 큰 점수를 부여하였다.

3.4 매개변수 불확실성 지수 산정 및 주요 매개변수 선정

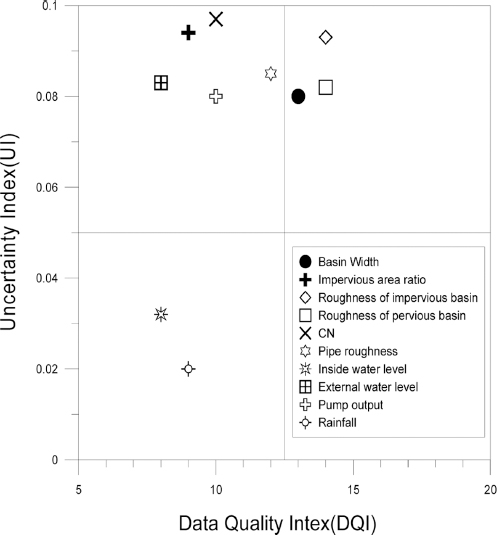
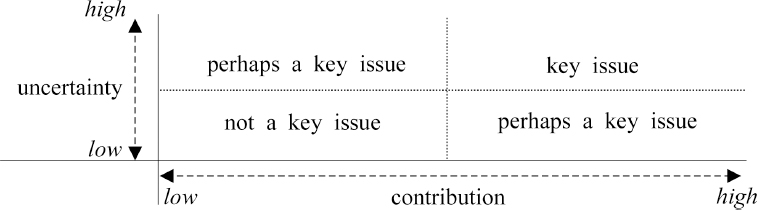
본 연구에서는 주요 매개변수를 선정하기 위해 Heijungs(1996)가 제안한 기여도 및 불확실성에 따른 주요 데이터 선택 사분면을 이용하였다. 제안된 그래프의 x축은 기여도를 나타내며, 자료의 품질평가 결과인 DQI, y축에는 불확실성 지수를 적용하였다. 결과 그래프의 각 사분면의 정의는 Heijungs(1996)에 따라 1사분면은 가장 중요한 자료(key issue), 2,4사분면은 중요한 자료가 될 가능성이 있는 자료(perhaps a keyissue), 3사분면은 중요하지 않은 자료(not a key issue)를 의미한다.

주요 매개변수를 선정하기 위해 Table 5의 매개변수 불확실성 지수와 Table 6의 Pedigree matrix를 이용한 불확실성 인자 점수 총합(DQI)을 이용하여 Fig. 2와 같이 나타내었다. 1사분면은 잠재적인 불확실성 요소가 크며, 2,4사분면은 연구의 목적에 따라 선택적인 매개변수를 의미한다. 3사분면은 불확실성 요소 및 매개변수 자체의 대표성을 지니고 있기 때문에 분석대상에서 제외 가능 한 매개변수를 의미한다.

Fig. 2

Method to Distinguish the Key Data from the Data that is Certain and Hardly Contributes to the Results.

각 지표점수의 총합인 DQI(Data Quality Intex)를 산정하게 된다. DQI 값이 낮을수록 정확한 데이터 값을 의미하여 이와 반대로 점수가 커질수록 불확실성이 크다는 의미를 뜻하게 된다.

분석결과 유역폭, 투수 및 불투수유역의 조도계수가 1사분면으로 불확실성도 크며 Pedigree matrix 종합 점수도 높게 나타나 분석시 우선적인 매개변수로 선정하였다. 불투수면적비율, CN, 관 조도계수, 외수위, 펌프 토출량의 경우 불확실성 지수는 높게 나타났지만, 데이터품질지수인 DQI는 낮게 나타나 필요시 선택적인 매개변수로 선정하였다. 마지막으로 3사분면에 포함된 내수위 및 강우량의 경우 불확실성 지수 및 DQI가 낮게 나타나 필요 매개변수에서 제외가 가능하다고 판단된다. 불확실성 지수 및 DQI에 따른 매개변수 분류를 Fig. 3과 같이 나타내었다.

Fig. 3

Parameter Classification in Accordance with the Uncertainty Index and DQI.

4. 결론

최근 이상기후 및 도시화로 인한 홍수가 빈번히 발생하고 있으며, 도시의 홍수피해는 대부분 우수관망의 통수능 부족으로 인한 내수 침수로 분석되고 있다. 또한, 홍수로 인한 인명 및 재산피해를 줄이기 위해서는 정확한 강우-유출 해석이 이루어져야 하지만, 강우-유출 해석시 사용되는 매개변수의 정확한 입력값 및 모형에서의 불확실성을 내포하고 있어 정확한 해석을 하는데 어려움이 있다. 따라서 본 연구 에서는 강우-유출 해석 모형 및 내수 침수방어에 사용되는 빗물펌프장관련 불확실성 매개변수를 선정하였다. 또한, 주요매개변수를 선정하기 위해 Pedigree matrix를 이용하였으나, 데이터 품질평가시 어려움이 있어 본 연구에 맞게 Pedigree matrix를 수정하여 제안하였다. 제안된 수정 Pedigree matrix 및 정량화된 불확실성 지수를 이용하여 최종적인 주요 매개변수를 선정하였다.

본 연구에서는 모형 및 빗물펌프장 관련 불확실성 매개변수를 선정하기 위해 기존 문헌 등을 참고하여 선정하였다. 선정결과, 모형에서의 불확실성 매개변수는 총 6개(유역폭, 불투수면적비율, 불투수유역의 조도계수, 투수 및 불투수유역의 조도계수, CN, 관 조도계수)이며, 빗물펌프장 관련 불확실성매개변수는 펌프장 운영자료 4개(내수위, 외수위, 펌프 토출량, 강우량)로 선정하였다. 또한, 선정된 불확실성 매개변수의 정량적 평가를 위해 불확실성 산정 지수 공식 및 수정된Pedigree matrix를 이용하여 주요 매개변수를 선정하였다. 불확실성 산정 공식을 이용하여 불확실성 지수를 산정한 결과 CN의 불확실성 지수가 0.097, 불투수면적비율 및 불투수유역의 조도계수의 불확실성 지수가 0.094, 0.093으로 가장 높게 산정되었으며 가장 낮은 불확실성 지수를 산정된 매개변수는 강우량으로 불확실성 지수 0.020으로 산정되었다. 수정 Pedigree matrix의 종합 데이터 품질 지수(DQI)를 산정한 결과 투수 및 불투수유역의 조도계수의 DQI가 14로 가장 불확실성 정도가 가장 크게 나타났으며, 그다음으로 유역폭이 13으로 높은 불확실성 정도를 보였다.

주요 매개변수 선정은 Heijungs (1996)가 제안한 사분면을 이용하였으며, 불확실성 지수 및 Pedigree matrix의 DQI를 이용하여 사분면으로 구분하였다. 1분면의 경우 필수 분석데이터로 불확실성요소가 크다는 의미이다. 1분면에 위치한 매개변수는 유역폭, 투수 및 불투수유역의 조도계수로 가장 불확실성 요소가 크게 나타났으며 3분면인 내수위 및 강우량의 경우 불확실성 지수 및 DQI가 낮게 나타나 필요 매개변수에서 제외가 가능하다고 판단된다. 불확실성이 높은 매개변수를 측정시 보다 정밀한 매개변수 측정이 필요하며, 강우-유출 해석 및 빗물펌프장 운영자료 검토시 주요 우선 매개변수 선정에 도움을 주리라 판단된다.