통계학적 가능최대강수량의 재현기간 추정
Estimating the Return Period for Statistical Probable Maximum Precipitation
Article information
Abstract
본 연구에서는 가능최대강수량(Probable Maximum Precipitation, PMP)을 통계학적으로 추정하는 간단한 대안이 제시된다. PMP는 물리적인 강우량 상한계로, 확률론적 개념과는 모순적이지만, 관측자료로부터는 물리적인 강우량의 상한계를 명확하게 규정할 수 없기 때문에, PMP를 확률론적으로 구하는 방법이 합리적일 수도 있다고 판단하였다. 10년 이상의 관측자료를 보유한 기상청 ASOS 80개 지점의 일 강우량 자료를 이용하여 산출한 Hershfield의 km 은 각 관측 지점의 연 최대 시계열의 평균의 선형함수로 주어지는 형상 매개변수를 가지는 GEV 분포에 적합한 것으로 나타났다. 또한, 본 연구의 방법을 검증하기 위하여 우리나라에서 가장 오래된 15개 지점 자료(1961-2017, 57년)가 이용되었다. Hershfield의 통계학적 PMP와 수문기상학적인 PMP는 지점별로 다소 상이하였으나, 적용된 지점들 모두에서 일 강우량 PMP의 재현기간은 대략 20,000,000년인 것으로 추정되었다.
Trans Abstract
This study proposes a simple alternative to statistically estimate the Probable Maximum Precipitation (PMP). The PMP is the upper limit of physical rainfall depth and is contradictory to the concept of probability. However, since the upper limit of physical rainfall depth cannot be identified clearly from observed data, it was judged that making a probabilistic estimation of PMP might be reasonable. Hershfield's km, calculated from the daily rainfall depth recorded at 80 stations of the Automated Synoptic Observing System (ASOS) with more than 10 years of observations, was fitted to the Generalized Extreme Value (GEV) distribution with a shape parameter given as a linear function of the average of the annual maximum of the time series at each observation site. Data from the oldest 15 sites in Korea (1961-2017, 57 years) were used to verify the methodology suggested in this study. Hershfield's statistical PMPs and the hydro-meteorological PMPs were somewhat different; however, the return period for the PMPs in terms of daily rainfall depth was estimated to be approximately 20,000,000 years at all sites studied.
1. 서 론
가능최대강수량(Probable Maximum Precipitation, PMP)은 세계기상기구(World Meteorological Organization, WMO, 2009)에 의하면 ‘특정유역에서 주어진 지속기간에 대한 물리적인 상 한계치에 가까운 강수량’이라고 정의되고 있다.
Lee (2006)에 따르면 수문학적 설계규모의 실질적인 상한계는 지구규모의 수문순환으로, 지구상의 물의 총량은 일정하므로 유한하다고 할 수 있다. 상 한계가 없다는 것은 물리적으로 비현실적이라고 볼 수 있다. 이러한 상 한계는 가능한 최대 규모의 수문사상으로 정의될 수 있으며, 특정 장소에서 최대의 가용한 수문학적 자료를 바탕으로 추정된다. 상 한계에 대한 불확실성의 범위는 정보의 신뢰성, 기술 지식 그리고 분석의 정확성에 달려있으며, 정보 및 지식 그리고 분석기술이 향상됨에 따라 상 한계는 진정한 상 한계와 비슷하게 되고 불확실성의 범위는 줄어들게 된다. 상 한계는 발생 확률을 모르기 때문에 확정론적으로 취급되며, 설계규모를 낮춤으로서 확률 또는 재현기간에 바탕을 둔 방법이 적용되기도 한다. 이와 같은 기준에서 수문사상의 규모는 비교적 작아 상대적으로 자주 관측되는 범위 내에 나타나게 된다. 따라서 빈도해석을 위한 장기간의 수문자료가 있다면 수문사상의 발생확률은 적절하게 산정될 수 있다. 또한, 확률론적 방법은 확정론적인 방법보다 덜 주관적이며 더 이론적으로 다루어질 수 있다(Papalexiou and Koutsoyiannis, 2006).
Hershfield의 통계학적 PMP 산정방법은 현재 세계적으로 통계학적인 방법으로 PMP를 추정하는 표준 방법으로 제시되어있다(WMO, 2009). Hershfield에 의해 개발된 절차는 아래와 같은 빈도방정식에 근간을 두고 있다(Hershfield, 1961).
여기서 hm은 관심 지점에서 주어진 지속기간에 대한 관측 최대 강수량이고,
본 연구에서는 Koutsoyiannis (1999)에서 적용된 Hershfield의 통계학적 PMP 추정방법에 대한 확률론적 해석을 기반으로, 이러한 방법을 우리나라의 관측자료에 적용함으로써 우리나라 PMPs의 재현기간을 살펴보는데 목적이 있다. 앞서 언급한 바와 같이 PMP는 물리적인 강우량 상 한계로 완벽하게 산정할 수 없고, 발생 확률 또한 알지 못하기 때문에 추정된 PMP가 전적으로 신뢰성이 있는 것은 아니다. 그러나 PMP는 대형 수공구조물의 설계 시 기준이 되는 강수량이며, 기존 수공구조물의 안정성 평가에도 유용하게 적용된다. 최근 대규모 거대재난에 대비한 대피계획수립에 PMP를 활용하려는 움직임이 있으며, 기후변화의 영향을 반영한 거대재난사상 시나리오를 수립하는 용도로도 이용되는 등 PMP에 대한 국내외 연구가 활발히 수행되고 있다(Lee, Park, Kim, et al., 2016). 기후변화 시나리오에 따른 PMPs 변화가 수문기상학적 방법으로 산출되었으며(Lee, Park, Lee, et al., 2016), 미래 이슬점의 변동에 따른 PMPs 변화가 분석되었다(Lee and Kim, 2016). Kim et al. (2016)에서 시⋅공간적 특성을 고려하여 유역규모의 PMP 산정방법을 개발하였고, 핵발전소 및 충주댐 유역 지역을 대상으로 기후변화 시나리오에 따른 PMP가 산정되었다(Lee, Jang, et al., 2017; Lee, Jo, et al., 2017). 또한, 본 연구에서 사용한 통계학적 PMP 방법을 이용하여 Choi et al. (2015)은 1일 PMP 산정 후 추세분석을 수행하였으며, 미래 기후변화 RCP 시나리오를 이용하여 1일 PMP 산정 및 신뢰성 있는 PMP를 산정하기 위한 최소관측기간 선정에 대한 연구가 선행되었다(Sim et al., 2015, 2017).
2. Hershfield 방법에 따른 우리나라 자료의 통계학적인 해석
본 연구에서는 기상청 ASOS 자료를 이용하여 강우 관측년 수가 10년 이상인 강우관측소 80개 지점에 대한 시간강우량 자료를 수집하였다. Table 1에 나타난 바와 같이 지점별 자료기간에 따라 3개의 등급으로 나누어 자료를 분석하였다. 지점별 연 최대 시계열을 작성하고 Eq. (1)을 이용하여 지점별 km을 계산하여 1.6에서 6.0까지 0.2간격으로 총 22개 구간으로 정리하여, 자료기간의 각 등급별 최소 및 최대 km 구간을 도출하였다.
자료기간 n의 영향을 무시하고(추후 고려), 모든 등급의 자료를 통합한 후, Weibull 공식을 이용하여 다음과 같이 확률변수 Km의의 비초과확률을 계산한다.
여기서 r(km)은 Km≤km인 자료의 개수이고, r′은 총 자료의 수(80)이다. 즉, F*(1.6)이 가장 작은 값을 가지며, F*(6.0)이 가장 큰 값을 가진다. Eq. (2)은 앞서 계산된 km값의 22개 구간의 대하여 계산된다.
Fig. 1은 이와 같이 산정된 F*(정확하게는 -ln(-lnF*))에 대한 km 관계곡선을 Gumbel 확률지에 도시한 결과이다. 추정된 GEV 분포의 매개변수는 α=0.733, β=-0.0479, x0=2.6845이다(매개변수에 대한 설명은 Eq. (4) 참조). 물리적 상한계가 존재하려면 Fig. 1에서 F*가 1에 가까워질수록(Fig. 1의 횡축의 값이 오른쪽 끝으로 향할 때) km이 특정한 값(예를 들어 km = 15)으로 수렴되는 형태로 나타나야하지만, Fig. 1의 km은 계속 증가하는 형태임을 살펴볼 수 있으며, 적어도 수렴되는 형태는 아닌 것을 알 수 있다. 도시된 점들이 Gumbel 확률지 상에서 직선을 형성한다면 km은 Gumbel 분포를 따른다고 볼 수 있으나, Fig. 1이 곡선 형태는 형상 매개변수를 갖는 GEV 분포를 따른다고 가정하는 것이 타당하며, GEV 분포에 적합한 결과가 Fig. 1의 실선이다. 결론적으로, Fig. 1에서 관측 최대값 km = 6은 물리적인 상 한계가 아니며, 더 많은 자료가 축적된다면 더 큰 값을 가질 가능성이 매우 높다.
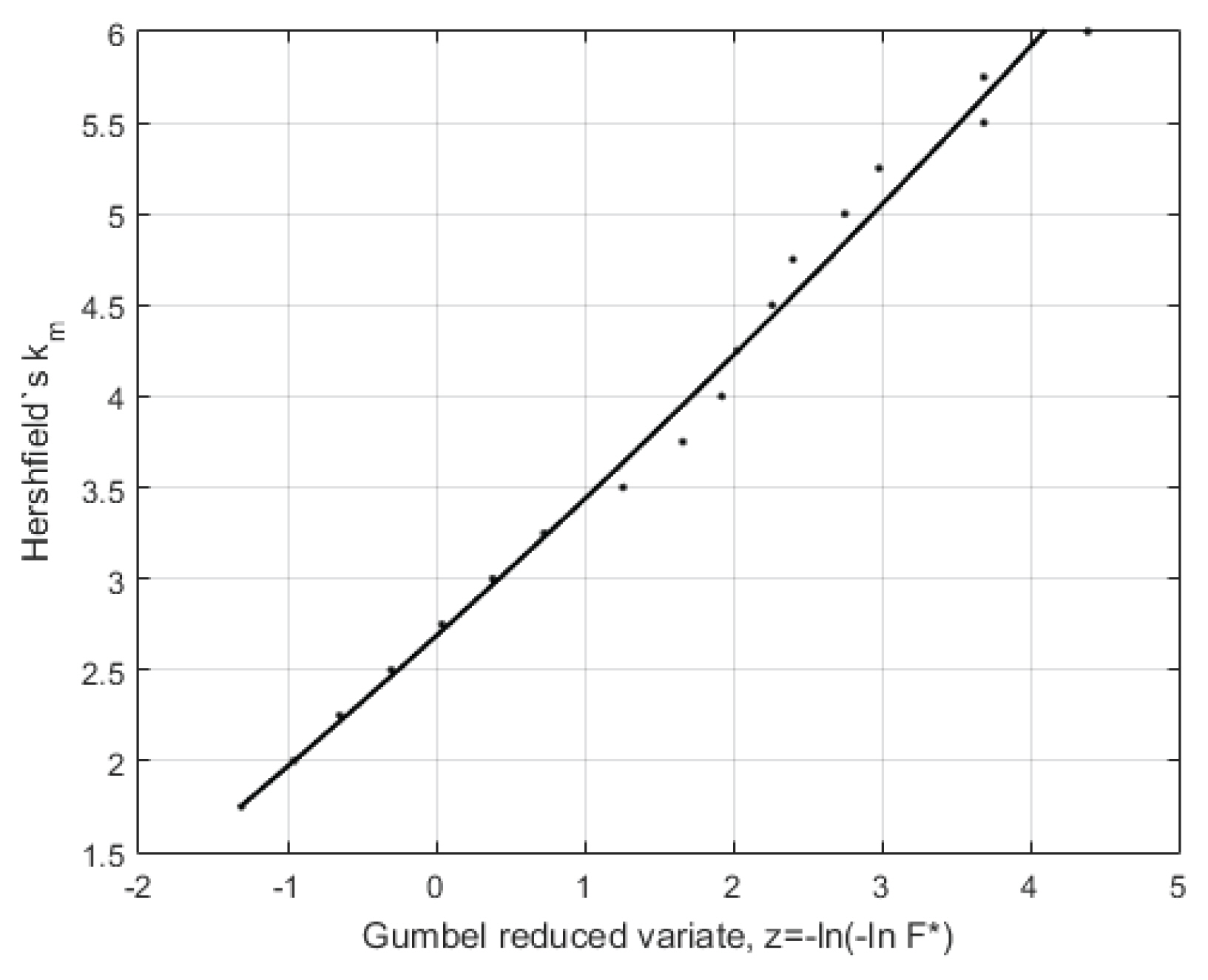
Empirical (dots) and GEV (continuous line) Distribution Function of Maximum Standardized Variate km for all Classes of Record Length (on Gumbel probability paper)
Gumbel 분포와 GEV 분포의 누가확률밀도함수는 각각 아래 Eqs. (3) and (4)와 같다.
Eqs. (3) and (4)에서 x은 본 연구의 경우 km을 의미한다. 여기서 α, β, x0은 각각 축적, 형상, 위치 매개변수이다. α와 x0은 무차원이며, x의 범위는 β의 부호에 따라 결정된다. Eq. (3)은 Eq. (4)에서 β=0인 경우의 분포함수이며 매개변수로 α와 x0가 사용된다.
Fig. 1에서의 분석은 km에 대한 자료기간 n의 영향을 고려하지 않은 것이다. 자료기간의 영향을 고려해야 할 이유는 아래와 같다. 첫째, 자료기간이 더 길어진다면 더 큰 값의 km이 나타날 것이다. 둘째, km은 표본 평균과 표준편차에 의해 표준화된 값이므로, 자료기간이 더 길어질수록 km계산에 필요한 평균 및 표준편차가 더 정확하게 추정될 것이며 이는 km의 추정이 보다 더 정확진다는 것을 의미한다. Eq. (2)을 다시 사용하여 Fig. 1과 같은 방법이지만 자료 전체를 하나로 통합하지 않고, Table 1의 자료기간 등급별로 각각 나누어 계산한 결과를 Fig. 2에 도시하였다. 즉, 여기서 r′은 각각 등급별 총 자료수이다. Fig. 2에서 알 수 있듯이, 낮은 비초과확률 구간(그림에서 왼쪽)에서는 자료기간이 짧은 등급(예를 들어, 10-29년)의 분포곡선이 자료기간이 긴 등급(예를 들어, 30-45년)의 분포곡선보다 아래쪽에 위치하고 있다. 이는 자료기간이 길어질수록 더 큰 값의 km을 가질 가능성이 높기 때문이다. 그러나 높은 비초과확률 구간(그림에서 오른쪽)에서는 이러한 현상이 명확하게 나타나지 않으며 일부 경우에는 역전되는 것을 확인할 수 있다(예를 들어, 30-45년 등급의 분포곡선이 >46년 등급의 분포곡선보다 더 큰 값). 이는 아마도 자료기간이 짧은 등급에서의 평균 및 표준편차의 추정이 부정확하기 때문도 한 가지 원인일 것으로 판단된다.
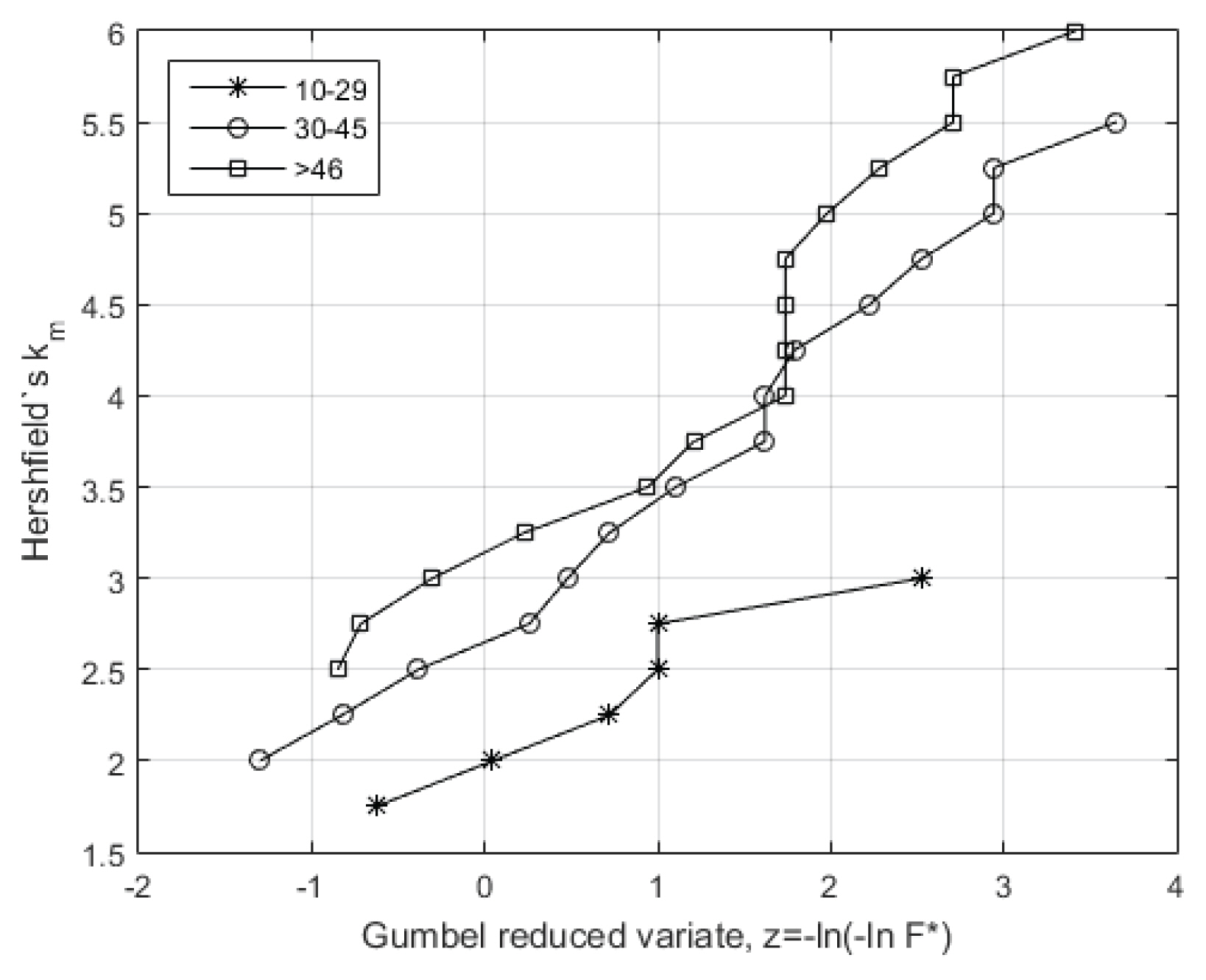
Empirical Distribution Functions of Maximum Standardized Variate km for Each Class of Record Length (on Gumbel probability paper)
사실 확률변수의 평균과 표준편차의 추정에서 자료기간이 갖는 한계를 극복하는 것을 불가능하다. 그러나 지점별 관측 최대 km의 확률분포를 분석하는 것 대신에 아래와 같이 모든 지점에 대하여 연 최대 ki에 대한 확률분포를 분석한다면 자료기간의 한계를 일부 극복할 수 있을 것이다.
여기서 hi, i=1, 2, ..., n은 어떤 지점에서 i번째로 관측된 연 최대 강수량이다. Km과 Ki의 누가확률분포를 각각 F*( )및 F( )라 할 때, 모든 ki은 서로 독립이므로 F*(k)=[F(k)]n이 된다. 따라서 Eq. (2)로부터 F*(k)가 주어진다면, F(k)의 분포는 아래와 같이 경험적으로 추정이 가능하다.
Table 1의 자료기간 등급별로 위 과정을 수행한다. 이때, Eq. (6)의 n은 각 자료 구간에 있는 지점들의 자료기간 평균을 적용하였다. 이와 같이 적용하면 총 지점-년 자료의 수가 3,405가 되므로, 분석되는 지점들의 총 지점-년 자료의 수 3,405와 정확하게 일치하게 된다. 이 때, F(k)의 추정은 앞서 사용된 km의 22개 구간에 대해서만 가능하다. 자료기간 등급별로 추정된 경험적인 확률분포 F(k)을 Fig. 3에 도시하였다.
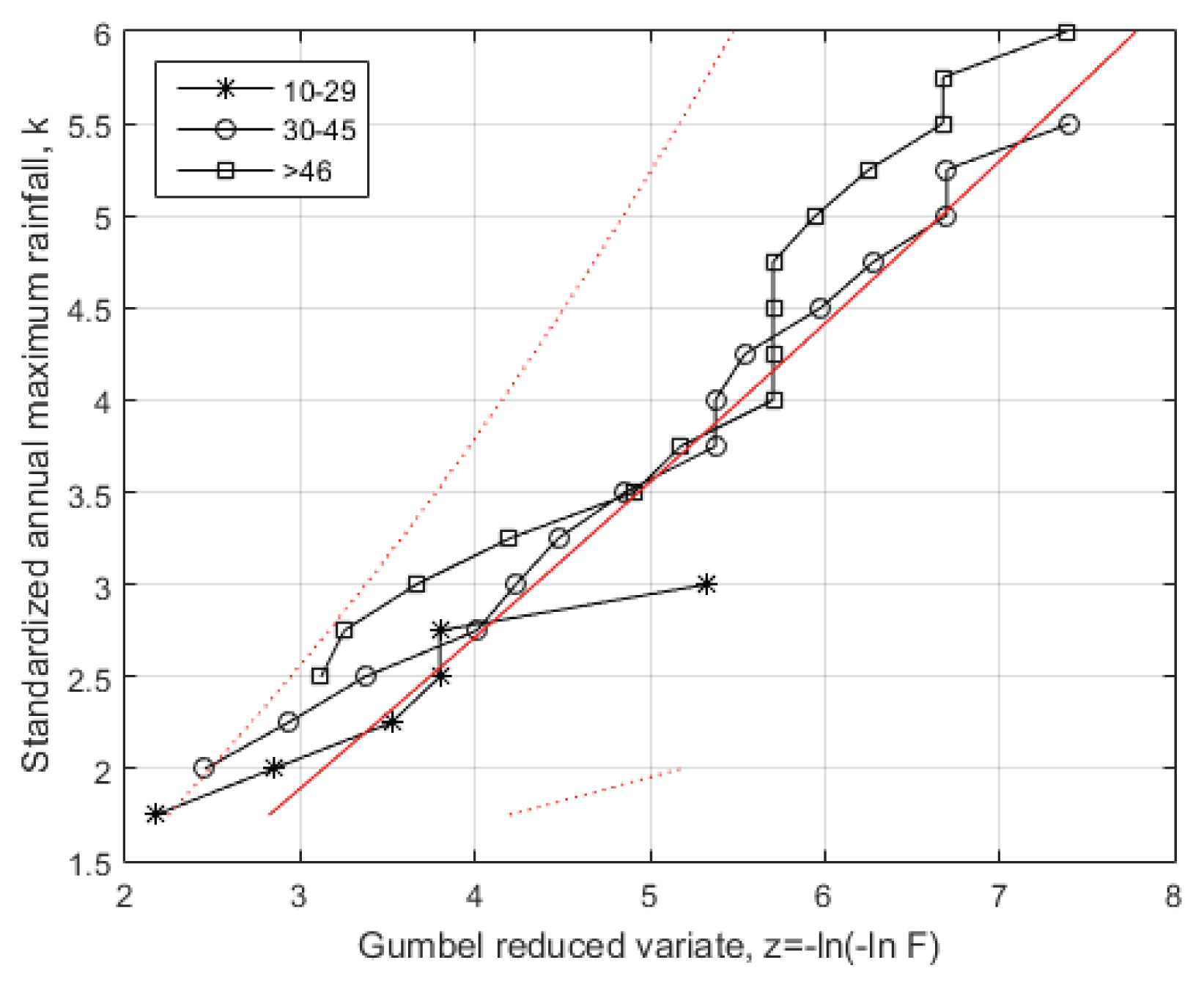
Empirical Distribution Functions of Standardized Rainfall Depth k for Each Class of Record Length (on Gumbel probability paper)
Fig. 2에 도시된 자료등급별 확률분포 F*(km)의 차이가 Fig. 3의 확률분포 F(k)에서는 매우 작아졌음을 살펴볼 수 있다. Fig. 3의 GEV 분포의 작성 과정(붉은 색 실선과 붉은색 점선)은 추후 3장에서 설명할 것이다. 그림의 점선은 적합된 GEV 분포의 개략적인 99% 신뢰구간이며, 특정 F값에 대한 99% 신뢰구간 값은 F±2.576σF로 계산된다. 여기서 2.576은 99% 신뢰구간에 대한 표준정규분포의 분위수 값이며, 자료의 크기 m′에 대한 F의 표준편차는
3. 지속기간 24시간 강우량에 대한 Hershfield 방법의 대안 제시
2장에서 다루었던 개략적인 분석은 다양한 자료기간 등급에 따라서 k의 확률분포 특성이 크게 바뀌지는 않는다는 것을 나타내고 있다. 물론 자료기간 등급을 분리하는 기준이 지점의 자료 년 수가 가장 적절한 것은 아닐 것이다. 기후조건 등 다른 여러 가지 조건이 k의 확률분포에 영향을 미치는지 여부를 살펴볼 필요가 있을 것이나, 이는 본 연구의 범위를 넘는 것으로 판단되어, 추후 연구로 남겨두었다.
그보다는 모든 자료를 하나로 통합하여 F(k)을 살펴볼 필요가 있다. Eq. (6)으로부터 등급 i에 대한 경험적 확률분포 Fi(k)을 계산할 수 있다. mi′은 등급 i의 지점-년의 수이며, mi(k)은 등급 i에 속한 k들 중에서 특정 k보다 작거나 같은 자료의 개수를 의미한다.
모든 등급 i에 대해 mi(k)을 통합하여 모든 자료에 대한 m(k)을 구하고, 마찬가지로 모든 mi′을 더하면 총 지점-년수(3,405)가 되므로 아래와 같은 경험적 확률분포 F(k)을 구성할 수 있다.
F(k)의 계산은 앞에서와 마찬가지로 앞서 사용된 km의 22개 자료 구간에 대하여 수행되어졌다. 즉, k가 1.8에서 6.0까지 0.2 간격으로 22개의 k값에 대하여 F(k)가 추정된다. 이렇게 추정된 F(k) 값의 범위는 0.8922 ~ 0.9993916이다. 즉, F(k) < 0.8922에 대한 정보는 제공하지 못하며, 이는 재현기간 9.3년 이하에 대한 정보는 추정이 불가능함을 의미한다. 그러나 공학적인 분야에서 필요한 정보는 높은 재현기간에 대한 사항이므로, 이 정도의 정보 손실은 본 연구에서 유의하게 크다고 볼 수는 없을 것으로 판단하였다.
Fig. 4에 이와 같은 방법으로 획득한 경험적 확률분포를 Gumbel 확률지에 도시하였다. 18개의 점(22개 자료기간 구간 중 4개의 구간의 값이 존재하지 않음)으로 나타낸 경험적 확률분포의 형태가 Gumbel 확률지 상에 도시되어있다. Fig. 3에서 언급한 GEV 분포에 적용시킨 결과가 Fig. 4의 실선이다(Fig. 3에서도 실선으로 표시). 2장에서 설명한 방법을 이용하여 99% 신뢰구간을 점선으로 도시하였으며, 단 m′ =3,405을 적용하였다. GEV 분포의 매개변수는 최소자승법을 이용하여 추정되었으며, 18개의 k 값별로 계산된 이론적인 -ln(-lnF(k))값과 경험적인 -ln(-lnF(k))값의 편차가 가장 작아지도록 최적화 과정을 수행하였다.
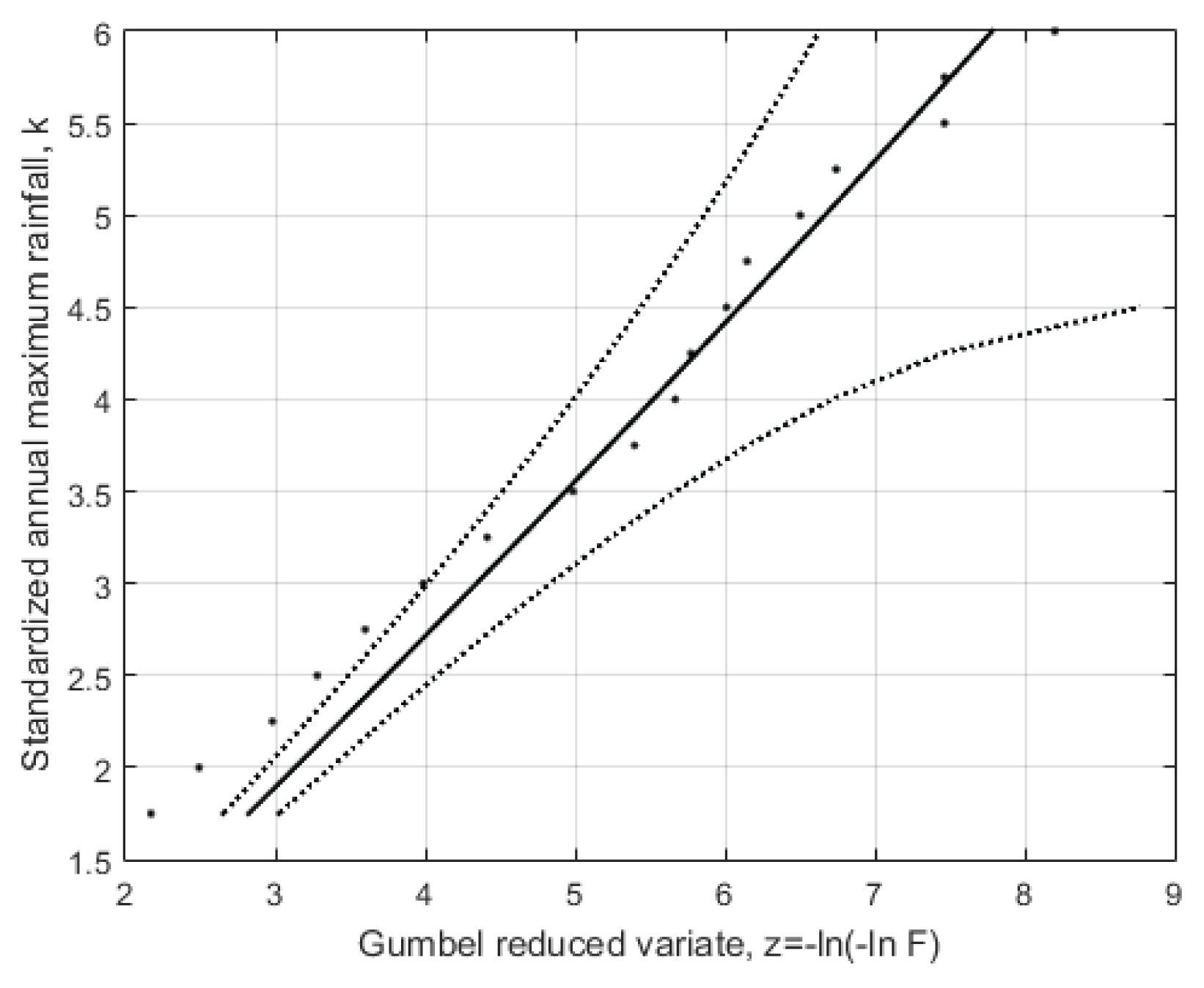
Empirical (dots) and GEV (continuous line) Distribution Function of Standardized Rainfall Depth k for all Data (on Gumbel probability paper)
그러나 매개변수 추정을 위한 최적화 과정 수행 시에 k은 표준화 변수이므로 k의 평균과 표준편차는 당연히 각각 0과 1이 되어야 할 것이므로, 이를 고려하여 매개변수를 추정하는 것이 필요하다. 엄밀히 말하면, 지점별로 표준화 과정을 이용하여 k을 구하게 되므로, 자료기간 등급별로 자료를 통합하거나 또는 모든 자료들을 통합할 경우 k의 표준편차가 반드시 1이 되는 것은 아니나, 1에서 크게 벗어나지는 않으므로 평균과 표준편차에 관한 제약조건을 매개변수 최적화 과정에 포함하는 것이 타당할 것으로 판단되었다. 추정된 GEV 분포의 매개변수는 제약조건을 반영한 유전자 알고리즘을 이용하여 α=0.755, β=-0.0238, x0 =-0.454으로 추정되었다.
평균이 0이고 표준편차가 1이라는 제약조건이 부여되면, 추정해야하는 매개변수는 형상 매개변수 β가 된다. GEV 분포의 식의 구조를 살펴보면 표본의 평균과 표준편차가 주어지고, 형상 매개변수 β가 추정되면 α와 x0은 자동적으로 계산되기 때문이다. 다만, 자료의 수가 적을 경우 β의 정확한 추정이 어렵게 된다.
k의 평균이 0이고, 표준편차가 1이므로, Eqs. (3) and (4)에 적용하면, Gumbel 분포와 GEV 분포의 누가확률밀도함수는 각각 다음과 같이 기술할 수 있다.
여기서 Γ( )은 gamma 함수이며, 결국 Gumbel 분포는 매개변수와 무관하게 단일한 형태의 함수가 되며, GEV 분포는 β 만의 함수로 표현됨을 알 수 있다. 앞서 추정된 GEV 분포의 매개변수 β=-0.0238와 k=15을 Eq. (10)에 적용하여 풀면, F(k)=0.99999994, 즉 17,540,000년의 재현기간을 갖는 것으로 분석된다. 대략적으로 Hershfield의 k=15에 해당하는 PMP는 20,000,000년 빈도에 해당한다고 볼 수 있다.
위의 결과는 세 가지로 요약될 수 있다. (1) 우리나라 연 최대 일 강우량 시계열을 GEV 분포를 적용하는 것은 타당하다고 볼 수 있다. (2) Hershfield의 PMP에 해당하는 표준화된 연 최대 강수량 km=15은 재현기간 약 20,000,000년에 해당한다. (3) GEV 분포의 형상 매개변수 β은 -0.0238의 값을 가진다.
Hershfield (1965)는 지점별 PMP 추정을 위하여 km=15대신에 해당 지점의 연 최대 시계열의 평균
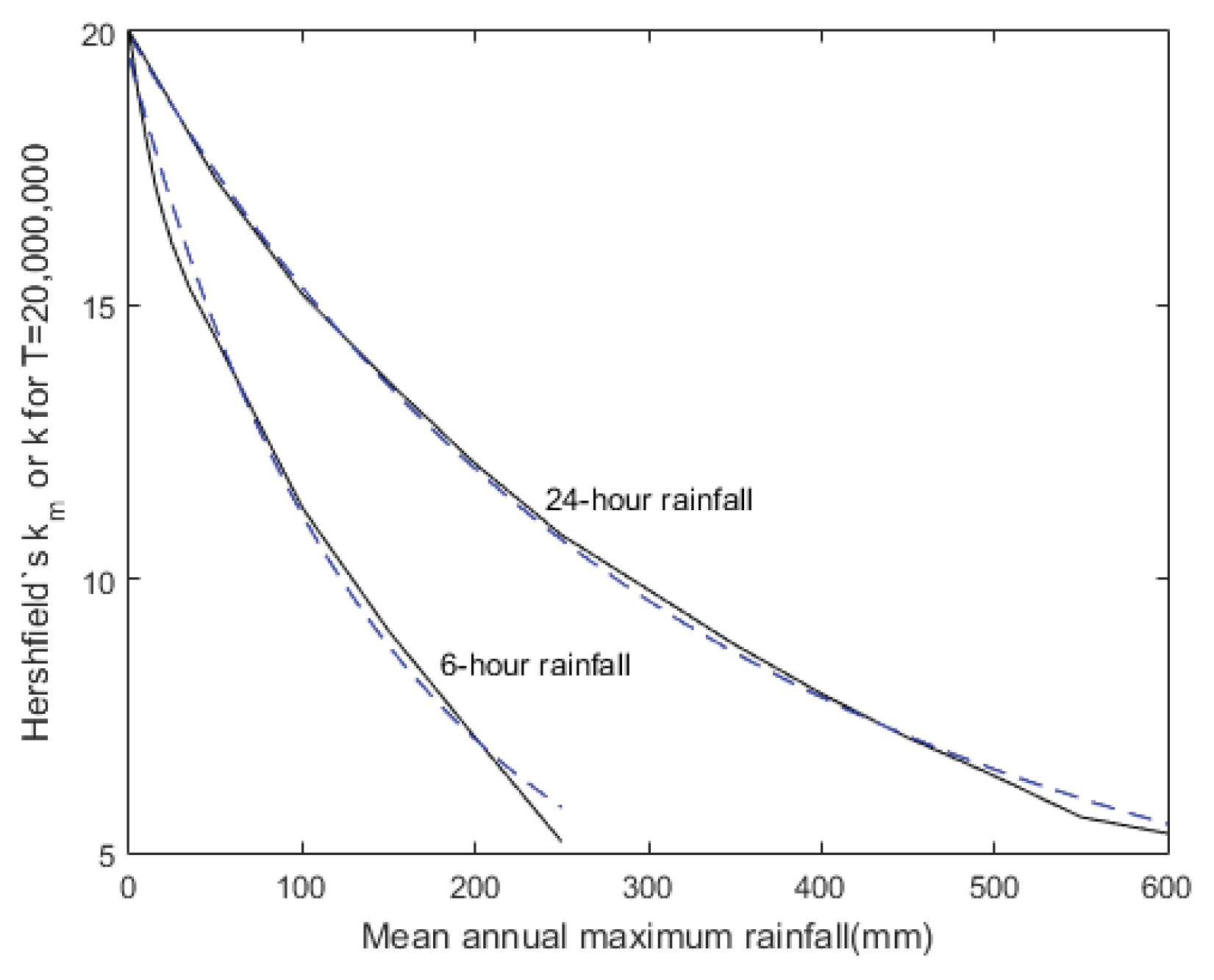
Comparison of Hershfield’s Empirical Nomograph for km, as a Function of the Mean Annual Maximum Rainfall and Duration d (dashed lines), with the Curves Obtained for the Proposed Alternative Formulation (k for T=20,000,000; continuous lines) by Applying Equations (9), (10) and (11)
노모그래프의 실선은 β와
T=20,000,000년에서 Eqs. (10) and (11)를 합성함에 따라 얻게 되는
Eq. (11)을 살펴보게 되면, 매우 높은
4. 제안된 방법의 검증
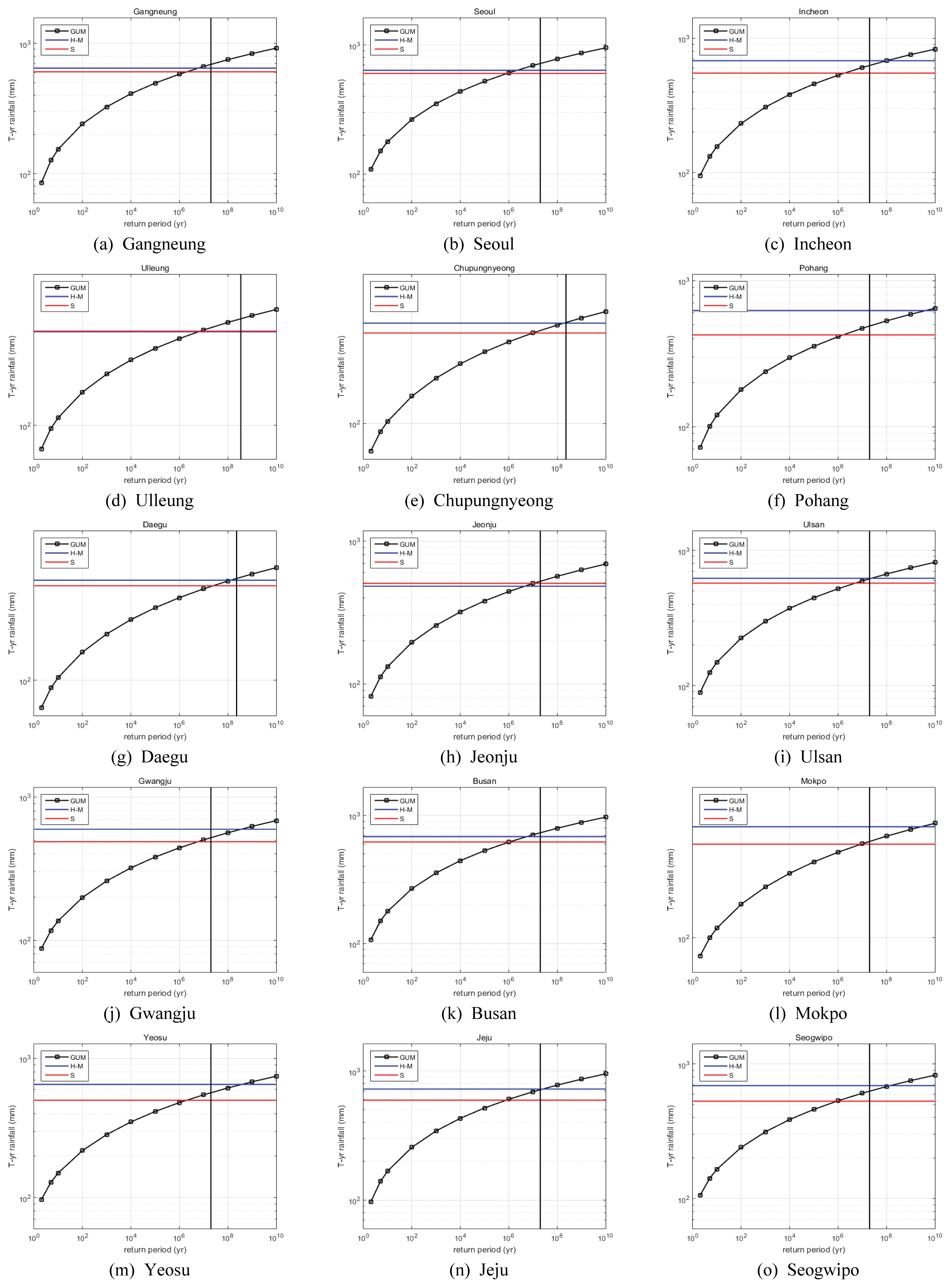
제안된 방법을 검증하기 위하여 기상청 ASOS 관측지점들 중 가장 오래된 15개 지점(1961-2017; 57년)의 강우자료를 이용하였으며, 지점별로 다양한 재현기간(2, 5, 10, 102, 103, …, 1010년)에 대한 확률강우량을 각각 추정하였다. 확률강우량은 각각 GEV 분포와 Gumbel 분포를 적용하였으며, 매개변수는 확률가중모멘트법을 적용하여 추정하였다. GEV 분포로 산정하였을 시에는 확률강우량이 지나치게 과대 산정되는 것을 확인하였으므로, Gumbel 분포를 적용시켜 확률강우량을 산정하는 것이 합리적일 것이라고 판단되었다. 또한 수문기상학적 PMP와 통계학적 PMP를 각각 산정하였는데, 통계학적 PMP는 Hershfield의 방법을 적용하여 본 연구에서 직접 추정하였으며, 수문기상학적 PMP의 경우에는 Lee and Kim (2018)의 연구에서 추정된 값(영향면적 25 km2 적용)을 이용하였으며, 이는 기존 WMO (2009)에서 제안하는 수문기상학적 방법을 기반으로 생산되었다. 또한 기존의 지형영향비 산정방법의 모호성에 기인한 주관적인 요소가 많아 객관적인 지형영향비의 산출이 어렵기 때문에, 본 연구에서 사용된 PMP는 지형영향비를 산악전이비로 대체하여 산출되었다. Eqs. (10) and (11)로부터 지점별 PMP에 대응하는 재현기간을 구할 수 있는데, 여기서 앞서 3장에서 언급하였듯이

Comparison of the Return Period by Point and the Corresponding Design Rainfalls and Hydro-meteorological (blue continuous line) and Statistical (red continuous line) Method for Probable Maximum Precipitation (24-hour rainfall)
추가적으로 지속시간 6시간을 기준으로 동일한 분석을 실시하였으며, Hershfield의 경험곡선(실선)과 비교하여 β와
T=20,000,000년에서 Eqs. (10) and (12)를 합성함에 따라 얻게 되는 지속시간 6시간에 따른
5. 결 론
Hershfield의 PMP 산정방법은 2,645개 지점 자료를 수집하여 총 95,000개의 지점-년 자료의 방대한 정보를 기반으로 PMP를 추정하는 방법으로, 세계 각지의 PMP 추정에 매우 유용하고 광범위하게 적용되고 있다. 그러나 PMP는 물리적인 강우량 상 한계로서 현재의 관측자료 수준으로는 완벽하게 산정될 수 없으며 그 발생 확률 또한 파악하기 어렵다. 본 연구에서는 Koutsoyiannis (1999)에서 적용된 Hershfield의 통계학적 PMP 추정방법에 대한 확률론적 해석을 기반으로, 이러한 방법을 우리나라의 관측자료에 적용함으로써 우리나라 PMPs의 재현기간을 살펴보고자 하였다.
기상청 ASOS 80개 지점 자료를 이용하여 총 3,405 지점-년 자료를 분석한 결과, PMP는 각 관측 지점의 연 최대 강우량 시계열의 평균의 선형함수로 주어지는 형상 매개변수를 가지는 GEV 분포(평균은 0, 표준편차는 1을 적용)를 사용하여 산정할 수 있으며, Hershfield의 k=15에 해당하는 PMP는 약 20,000,000년의 재현기간에 해당하는 강수량인 것을 살펴볼 수 있었다.
우리나라 PMP의 재현기간은 다른 문헌과 비교했을 때 비교적 큰 값을 나타낸다. 앞서 언급된 Koutsoyiannis (1999)는 PMP의 재현기간을 약 60,000년으로 추정한 바 있으며, Fontaine and Potter (1989)와 Foufoula-Georigiou (1989)는 100,000-1,000,000년 정도인 것을 제안한 바 있다. 또한 영국의 경우 PMP에 대해 추정된 재현기간은 200,000년(Austin et al., 1995), 그리스의 경우 여러 가지 확률분포를 이용하여 추정한 결과 작게는 4,200년에서 크게는 64,000,000,000년에 이르는 것으로 보고되었다(Koutsoyiannis and Baloutsos, 2000).
제안된 방법을 검증하기 위하여 우리나라 관측지점 중 가장 오래된 15개 지점 자료(1961-2017년; 57년)를 이용하여 지속기간 24시간과 6시간에 해당하는 PMP의 재현기간과 그에 따른 확률강우량을 각각 추정하였다. 전통적인 Hershfield의 통계학적 PMP 산정방법에 의해 추정된 PMP와 기존 연구에서 작성된 수문기상학적인 방법에 의한 PMP를 제안된 방법에 의해 산정된 PMP와 비교한 결과, 본 연구에서 수행한 방법으로 추정한 재현기간에 해당되는 확률강우량이 통계학적 PMP와 수문기상학적 PMP에 대체로 잘 부합하는 것으로 확인하였다.
Acknowledgements
이 논문은 부경대학교 자율창의학술연구비(2017년)에 의하여 연구되었음.