유량과 수질을 고려한 우수관망 모니터링 지점 선정
Determination of Monitoring Point Considering Water Quantity and Quality in Sewer Networks
Article information
Abstract
도심지 내배수시설은 우수의 원활한 이송을 통한 공공수역의 수질 보전뿐만 아니라 강우의 배제를 통한 유역 내 내수침수를 방지하는데 목적을 갖는다. 우수관망의 경우 내수침수에 대한 방재적인 측면에서 관로시스템 내부 흐름을 예측하기 위한 모니터링은 매우 중요하다. 모니터링 지점들은 주어진 예산 내에서 최대의 효율적인 자료의 획득이 가능한 지점들로 선정되어야 하지만 선정 기준 및 획득 자료에 대한 정량화된 평가 방법을 검토한 연구는 미흡하다. 본 연구에서는 도심지 내 발생하는 내수침수 및 수질 보전을 위한 효율적인 관리에 대한 필요성을 인식하고 유량과 수질을 고려한 우수관망 모니터링 지점 선정기법을 제안하고자 한다. 여기서 유량 및 수질을 고려한 모니터링 적정위치를 선정하기 위하여 엔트로피 기법을 이용하였으며, 유량과 수질이라는 서로 다른 차원의 두 가지 항목을 고려한 적합 방정식을 새로이 제안하고 이를 실제유역에 적용해 보았다. 본 연구에서의 우수관망 내 모니터링 지점선정에 관한 새로운 방법론은 내배수시설의 보다 효율적인 운영을 위한 것이며, 향후 실측 자료를 활용한 검⋅보정을 바탕으로 모니터링 지점으로부터 관내 흐름의 예측에 대한 정확도를 향상시킴으로써 내배수시설의 운영에 폭넓게 활용될 것으로 기대된다.
Trans Abstract
Urban drainage system aim at not only water quality conservation of public waters through smooth transfer of discharge but also prevention of flooding through the exclusion of rainfall. In case of a storm sewer network, it is very important in terms of disaster prevention as the internal flow of the urban sewer system is predicted through monitoring. Monitoring points are being selected as the ones available for acquisition of the maximum efficient data within the allocated budget, but insufficient is the research on examination of the quantified evaluation method of selection standards and acquired data. This study is intending to make a proposal of the selection technique of monitoring points of a urban sewer network in the light of the rate of water quantity and quality with the perception of the necessity of efficient management for prevention of flood. In addition, took account of entropy technique to select an appropriate location for the number of monitoring points in the light of the rate of discharge and water quality items, and put forward a monitoring-fit equation by taking into account the mutually different two sorts of items. Applied the developed model and methodology to an actual basin. It is thought that the new methodology regarding monitoring point selection in a urban sewer network, as a series of researches for efficient management of urban drainage system, will contribute to management by improving the accuracy of predictions on the basis of calibration/validation tapping into measurement data for the time to come.
1. 서 론
도심지 침수위험 저감을 위해서는 침수가 빈번히 발생하는 일대를 대상으로 유량에 대한 검토가 필요하다. 모니터링을 이용한 유량파악의 자료는 모든 지점의 유출량과의 연관성이며 주변 지점으로부터 연관성이 높은 지점을 선정하고 선정된 지점에서의 지속적인 모니터링이 필요하다(Yoo and Kim, 2003). 유량자료를 활용한 모니터링 관련 선행연구들을 살펴보면 Yoo and Kim (2003)은 엔트로피(entropy)기법 중 총 엔트로피를 이용하여 남한강 유역 내 주변 지점의 정보를 많이 나타내는 수위 관측지점 평가의 최적화 연구를 수행하였다. Ryu et al. (2012)은 엔트로피 이론 중 정보전달(transinformation)을 이용하여 우수관망 내 유출구의 유출량을 파악할 수 있는 모니터링 지점 선정 연구를 수행하였다. 여기서 모니터링 지점 선정을 유출구의 유출수문곡선과 유사한 지점을 선정하며 엔트로피 이론 중 정보전달의 총합으로 판단을 하였으며, 모니터링대상지점(target point)인 유출구와 모니터링 후보 지점 중 2개인 조건으로 기법을 제안하였다.
우수관망 내 모니터링의 목적은 유량자료 이외에도 수질자료 획득 및 예측에 있다. 특히 도시화로 인한 각종 오염물질의 유입량이 증가됨에 따라 수질오염문제가 증가하고 있으며, 효과적인 수질관리를 위해서는 수질오염측정망을 구축하고 지속적으로 모니터링 하는 것이 중요하다. 국내에서는 수질관리의 중요성을 인식하여 수질관리와 장기적인 대책 수립을 위해 공공수역에 대한 수질측정지점을 선정하여 수질조사를 진행하고 있다. 수질측정망에 대한 선행연구를 살펴보면 Kwon and Yoo (2001)는 엔트로피기법을 이용하여 대청댐 내 수질측정망의 중복된 정보를 나타내는 관측소를 제거하여 최적의 관측망을 선정하였다. Pack et al. (2007)은 K-mean 알고리즘을 적용하여 용담댐 저수지의 호 내 오염부하 유입에 영향이 적은 지점을 선별하고 모니터링 지점 대상에 제외하여 최적의 효과를 내는 연구를 수행하였다. 또한 Lee et al. (2011)은 기존 하천위주의 수질 모니터링 지점 선정 기법의 제약을 고려하여 우수관망 내 수질모니터링 지점 선정 기법을 제시하고 우수관망 내 수질측정망을 평가하였다. 다만 이러한 기존의 연구들은 유량 및 수질에 대한 모니터링을 독립적으로 평가하였으며, 실제 우수관망에서의 모니터링은 유량과 수질 두 가지를 동시에 고려하여 관측지점을 선정하여야 바람직하다.
따라서 본 연구에서는 유량과 수질을 동시에 고려한 모니터링 지점 선정에 관한 새로운 기법을 제안하였다. 적용대상은 서울특별시 영등포구 대림3 빗물펌프장 유역을 대상으로 하였으며, 빗물펌프장 유수지로의 유입량 예측 및 유역 내 수질의 대표성을 관측하기 위한 적정 모니터링 지점의 평가를 정량화하기 위하여 엔트로피기법을 이용하였다. 엔트로피기법 중 하나의 변량인 총 정보전달은 모니터링 후보지점과 관측지점 간 정보교환과정에서의 유사정보의 총량(불확실성의 감소량)을 의미하며, 결합엔트로피는 두 정보 간의 총 엔트로피에서 유사성(정보전달)을 제외한 독립성을 나타내는 정보량을 의미한다. 여기서 유량 및 수질에 관한 엔트로피 정보값을 축약하여 각각 유량엔트로피 및 수질엔트로피로 명명하였으며, 모니터링 후보 지점의 유량과 수질에 대한 각각의 엔트로피는 서로 다른 단위와 편차가 발생하므로 동등하게 평가하기 위해 정규화 과정을 수행하였다. 또한 모니터링 후보 지점의 정규화된 유량엔트로피와 수질엔트로피 값을 거리측정방법(Distance Measurement Method, DMM)에 대입하여 최대의 거리를 갖는 지점을 최적의 모니터링 지점으로 선정하였으며, 제안한 기법을 모니터링 적합 방정식이라 정의하였다. 본 연구의 수행절차는 Fig. 1과 같다.
Flow Chart in Study
2. 연구 방법
본 연구는 모니터링이 필요한 관측대상지점과 모니터링 후보 지점간의 유량 유사성 산정과 수질의 독립성 산정 방법으로 엔트로피기법을 사용하였다. 엔트로피 과정 후 모니터링 후보 지점의 유량과 수질의 엔트로피 값의 정규화 과정을 진행하여, 거리측정방법을 나타내는 모니터링 적합 방정식에 대입하여 모니터링의 적합도를 산정하였다.
2.1 엔트로피 이론
일반적으로 엔트로피는 무질서도 또는 불확실성의 척도로 알려져 있다. 정보이론에서는 Shannon and Weaver (1949)에 의해 엔트로피는 신호들의 정보교환 과정에서 발생하는 불확실성과 유사성을 수치적으로 표현하여 정보용량으로 정의된다. 정보교환의 과정으로 신호가 보내질 때, 신호의 정보량이 신호의 불확실성을 제거할 정도로 많아지면 신호의 불확실성은 감소되고, 이러한 불확실성의 감소정도에 따라 간접적으로 정보량을 측정할 수 있게 되는 것이다. 따라서 총 엔트로피가 클수록 그 지점의 유사성이 큼을 나타낸다. 본 연구에서 정의하는 엔트로피는 위 정보이론의 정의를 따른다.
엔트로피를 근거한 4가지 정보측정방법은 한계엔트로피(marginal entropy), 결합엔트로피(joint entropy), 조건부엔트로피(conditional entropy) 및 정보전달(transinformation)이다. 무작위 이산변수X에 대해 한계엔트로피H(X)는 다음 Eq. 1과 같이 정의된다(Yoo and Kim, 2003). 여기서, p(χn)의 χn)발생확률이다. 한계엔트로피H(X)는 X가 가지고 있는 정보용량 또는 불확실성량을 나타내고, N은 확률 p(χn)를 가지는 사건들의 수를 나타낸다.
만약 무작위 변수 χn과 관련된 yn이 있다면 yn을 이용해서 χn의 불확실성량을 줄일 수 있다. 이를 이용하여 X와 Y의 조건부엔트로피 XY는 Y를 알고 있는 경우 X에 남아있는 정보용량, 즉 Y의 정보로 나타낼 수 없는 X의 불확실성량을 나타내며 Eq. 2와 같다.
p(χnym은 X = {xn}과 Y = {ym}의 결합 확률,
엔트로피의 개념에서 만일 연속 무작위 변수 X가 확률밀도함수(Probability Density Function, PDF) f(x)를 따른다면 수문학적 시계열에 적용될 수 있다. 특히 대수정규분포를 따르는 X와 Y에 대한 한계엔트로피, 조건부엔트로피, 정보전달은 Amorocho and Espildora (1973)에 의해 유도된바 있다. Chapman (1986)은 일정하게 고정된 간격 ∆χ대신 변수의 범위에 비례하는 간격 ∆χ/χ를 적용하여 한계엔트로피와 조건부엔트로피 그리고 정보전달을 정의하였으며 Eqs. 4∼6과 같다. 이때 σz는 z(=lnχ)의 표준편차이고, ρzw는 z와 w(=lny)의 상관계수(correlation coefficient)를 나타낸다.
본 연구에서의 유량엔트로피는 Chapman (1986)의 정보전달을 이용하여 산정한다. 산정식은 다음 Eq. 7과 같다.
I(X1,...,Xn)는 n개의 모니터링 지점 수를 선정할 때의 유량엔트로피를 나타내며, X0는 모니터링이 필요한 관측대상지점을 나타낸다. 이들 중 Xa, Xb는 모니터링 후보 중 선정된 a, b지점을 의미하며, T(X0,Xa)는 관측대상지점과 a지점의 정보전달을 가리킨다.
수질엔트로피의 경우 독립성을 나타내는 Chapman (1986)의 한계엔트로피와 정보전달을 반영하였으며 다음 Eq. 8과 같다. Q(X1,...,Xn;Xc,...,XN)는 전체 N개의 모니터링 후보 지점 수 중 n개의 모니터링 지점 수를 선정할 때의 유량엔트로피를 의미한다. X1,...,Xn와 Xc,...,XN 는 지점들의 선정 유/무를 반영한 모니터링 후보 지점을 의미한다. 이때 X0는 모니터링이 필요한 관측대상지점을 가리키며, Xa, Xb는 모니터링 후보 중 선정된 a, b지점을 나타낸다.
2.2 수질모형
수질 모니터링 지점 선정을 위한 수질평가 항목은 우수관망에 영향력이 높은 TSS (Total Suspended Solids)를 고려하였다. 우수관망 내에서의 유량의 및 TSS의 산정은 미국 환경청(Environmental Protection Agency, EPA)의 Storm Water Management Model (SWMM 5.1)을 이용하였으며, TSS의 경우 SWMM 내부에 설정되어 있는 오염물 축적식 및 쓸림 식들 중 Tsihrintzis and Hamid (1988)이 제안한 방법(Eqs. 9 및 10)을 사용하였다. Lt는 시간 t에서의 오염물의 축적량(kg/ha), DD는 선행무강우일수(days), QFACT(2)는 축적(build-up)매개변수의 상관지수 그리고 QFACT(3)은 축척매개변수의 상관계수이다. 또한 Mt는 시간 t에서 유출되는 오염 부하(kg/sec), Qt는 유출률(m3/sec), WASHPO는 쓸림(wash-off)매개변수의 상관지수 그리고 RCOEF는 쓸림매개변수의 상관계수이다.
2.3 모니터링 적합 방정식
본 연구에서는 유량과 수질을 공동으로 평가하기 위한 방정식인 모니터링 적합 방정식을 제시하고자한다. 다만 유량과 수질은 단위의 차원이 달라 1대 1의 대응의 결과는 불합리하다. 따라서 본 연구에서는 하나의 통일된 평가결과를 도출하기 위하여 모니터링 적합 방정식은 거리척도방법(Distance Measure Method, DMM)을 이용하였다.
거리척도방법은 모니터링 지점으로써 적합평가를 위하여 우수관거 내 모니터링 후보지점의 유량엔트로피와 수질엔트로피를 동시에 고려한 거리를 척도하는 방법으로 현 모니터링 지점에 대한 적합평가를 정량적으로 나타낼 수 있는 방법에 해당한다. 거리척도방법은 원점(유량과 수질의 엔트로피의 최소값)으로부터 모니터링 지점의 유량과 수질의 엔트로피의 거리가 최대가 되는 지점을 채택하는 방법이다. 우선적으로 유량엔트로피와 수질엔트로피의 통일된 차원을 위하여, 지점별 유량 및 수질엔트로피는 정규화과정을 수행하며 다음 Eqs. 11 및 12와 같다.
NomalIn와 NomalQn는 n 지점의 유량엔트로피와 수질엔트로피의 정규화 값을 의미하며, In와 Qn은 n지점의 유량엔트로피와 수질엔트로피, IQmax와 IQmin은 전체 모니터링 후보 지점 중 유량엔트로피 최대값과 최소값을, Qmax와 Qmin은 수질엔트로피의 최대값과 최소값을 의미한다.
거리척도방법의 개념을 이용하여 정규화 유량엔트로피와 수질엔트로피를 적용시킨 모니터링 적합 방정식은 Eq. 13과 같다. 여기서, Dn은 n지점의 거리(적합도), NomalIn와 NomalQn는 n지점의 유량엔트로피와 수질엔트로피의 정규화 값을 의미한다.
Concept of DMM in this Study
3. 적용 및 결과
3.1 대상유역 및 적용강우
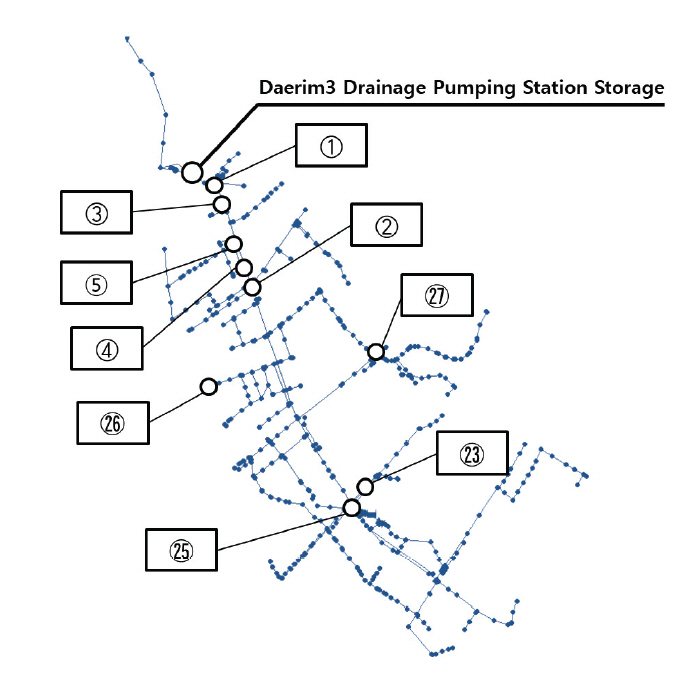
본 연구에서는 서울특별시 영등포구 대림3동 빗물펌프장 유역을 적용하였으며, 해당 유역의 우수관망 구성은 Fig. 3과 같다. 유역면적은 248.5 ha이며, 관망의 구성 지점은 508개의 맨홀지점과 1개의 유출지점, 1개의 빗물펌프장 유수지 그리고 1개의 빗물저류조로 구성되어있다.
Sewer Network of Applied Basin
Applied Rainfall Event
본 연구에서 관측대상지점으로 대림3빗물펌프장의 유수지 유입지점을 선정하였으며, 유량 모니터링 지점의 후보는 조기펌프가동을 위한 예측시간을 고려하므로 관측대상지점의 상류 322개의 맨홀지점을 대상으로 모니터링 선정을 진행하였다. SWMM을 바탕으로 수질항목의 모의에 있어 유역 내 환경변화가 발생할 때 TSS 수치가 급변하는 특성을 고려해야 한다. 각 지점의 대표 TSS는 도림천 2008년부터 2014년까지 7개년 동안의 TSS 평균값 12.63 mg/l를 반영하였다. 적용 강우는 설계빈도를 초과하는 30년, 50년, 80년 및 100년의 4개 재현기간과 각 빈도별 60분, 90분 및 120분의 강우 지속시간에 따른 총 12개 사상들에 대하여 강우의 시간분포 Huff 3분위를 적용하였다.
3.2 유량엔트로피 및 수질엔트로피
12개 강우사상별 322개의 모니터링 후보 지점의 결과는 x축을 유량엔트로피, y축을 수질엔트로피로 나타내었으며 다음의 Fig. 4와 같다. 강우사상별 최대거리가 발생하는 지점 중 최다지점으로 ①의 지점이 6개의 강우사상에서 나타났으며, 3개의 강우에선 ③지점, 2개의 강우에선 ②지점, 1개의 강우에서 ④지점으로 나타났다. Fig. 4를 통해 거리결정에 주로 유량이 관여함을 알 수 있었다. 유량엔트로피 0.2~0.5 사이값을 중심으로 지점들이 세로형태의 밀집된 양상이 나타났으며, 수질엔트로피는 0.1, 0.5~0.6 부근에 집중되어 있음을 알 수 있다.
Entropy Graph for Water Quantity and Quality (rainfall event 1~12)
3.3 모니터링 적합도 결과
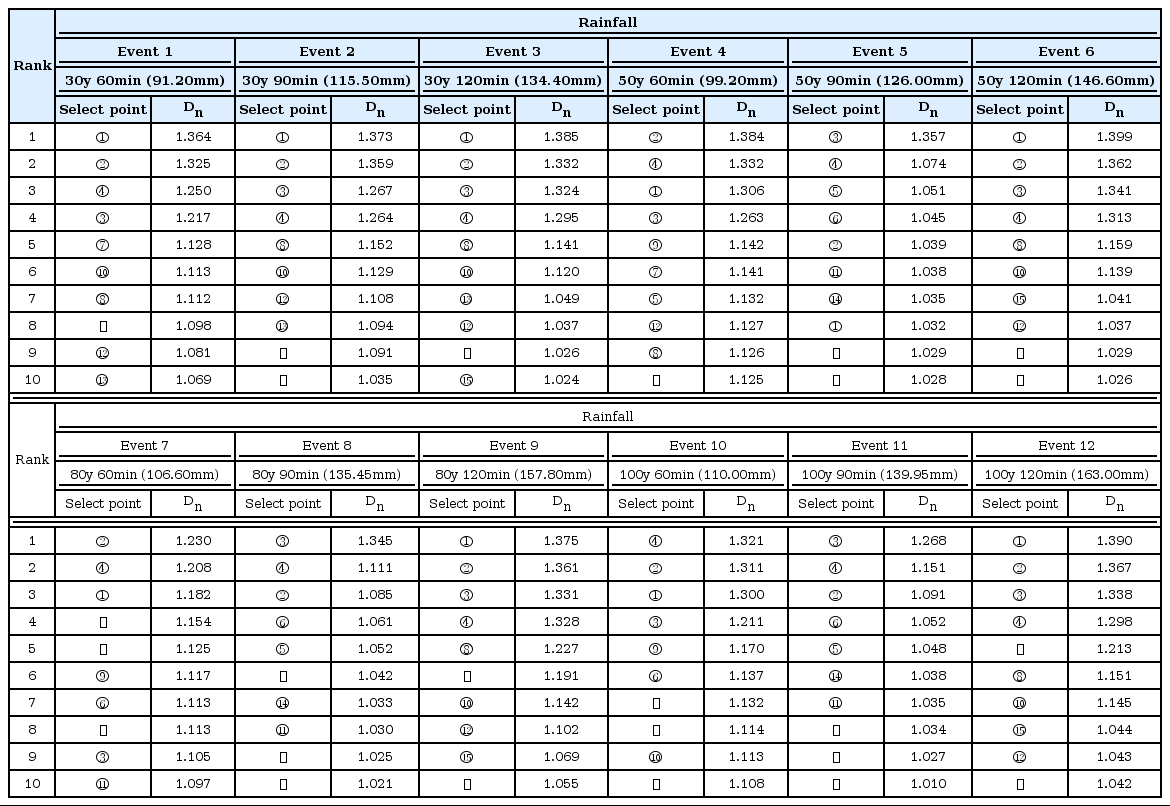
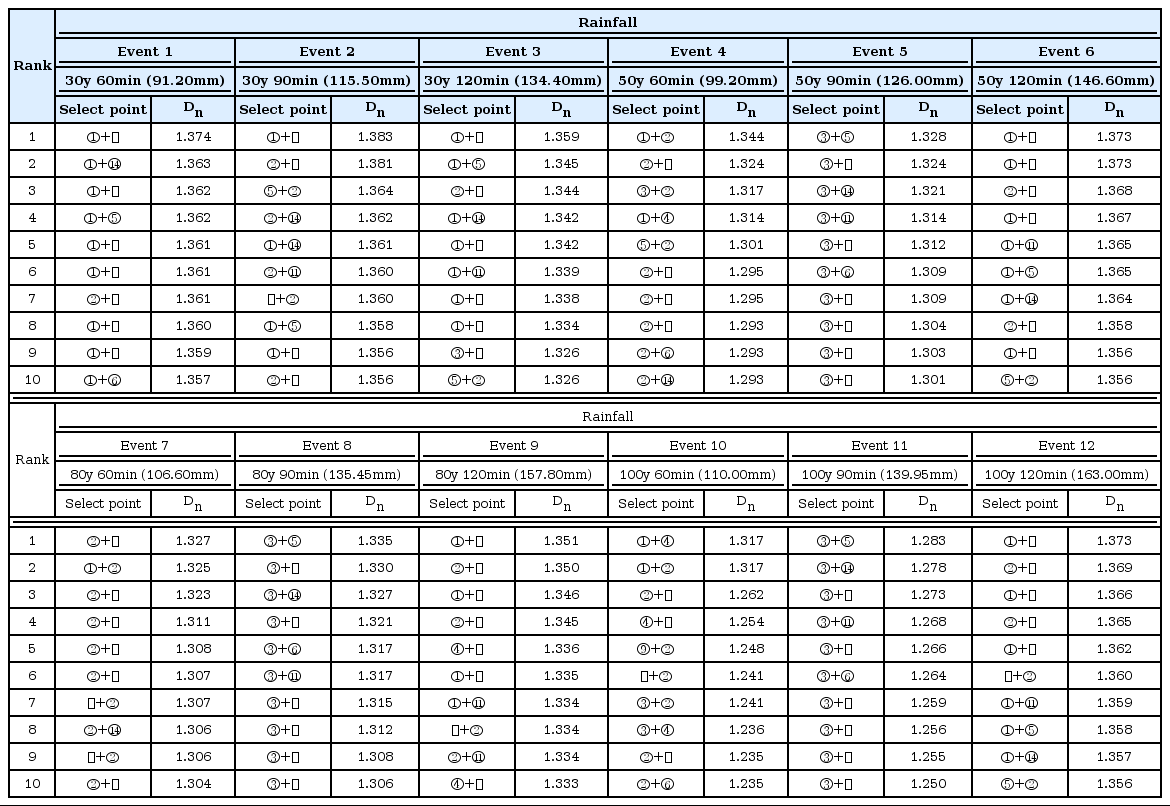
본 연구에서는 예산의 제약을 고려하여 모니터링 지점수가 1개와 2개인 상황을 분석하였다. 모니터링 지점 별 적합도를 산정하였으며, 322개의 모니터링 후보 지점 중 상위 10위 지점을 나타내었다. 모니터링 지점 수가 1개의 결과는 Table 2와 같으며, 모니터링 지점 수가 2개의 결과는 Table 3과 같다. 모니터링 지점 수가 1개인 결과는 12개의 강우사상 중 1위를 차지한 지점은 ①지점, 2위는 ③지점, 3위는 ②지점, 4위는 ④지점으로 나타났다. 그 중 빈도가 가장 높은 ①지점이 모니터링 지점으로 적합하다고 볼 수 있다. 나머지 상위 2-10위 지점은 강우사상별 빈도가 높은 지점들로 나타났다. 모니터링 지점 수가 2개인 결과는 12개의 강우사상 중 1위를 차지한 지점은 ①과 ㉕지점이며, 2위는 ③과 ⑤지점, 3위는 ①과 ㉖지점의 조합으로 나타났다. 이 중 빈도가 가장 높은 지점은 ①과 ②지점의 조합으로 나타났다. 이는 모니터링 지점 수가 1개인 결과를 비롯하여 상위 1, 2순위로 도출된 ①지점과 ③지점이 모니터링 지점수가 2개일 때에 기여도가 높음을 알 수 있다. 이상의 결과에서 엔트로피 방법을 이용해 선정한 모니터링 지점이 안정적으로 하류지점의 변동성을 예측할 수 있는 것을 알 수 있다. 다만 본 연구에서 수행되지 않은 관측유량과 선형회귀식화를 바탕으로 선행시간 만큼의 변동성 예측이 가능할 것으로 판단된다.
Fitness Result of Top 10 Rank (1 monitoring point)
Fitness Result of Top 10 Rank (2 monitoring point)
4. 결론 및 고찰
본 연구에서는 유출특성 중 유량과 수질을 동시에 고려한 모니터링 지점 선정 기법과 이에 대한 결과를 제시하였다. 유량과 수질을 동시에 고려한 모니터링 적합도 방정식의 목적은 우수관망 내 유출특성의 파악과 이를 통한 관리이며, 이를 위한 대표적인 유출특성은 유량과 수질이다. 따라서 단일 유출특성을 고려한 지점 선정이 아닌 복합 유출특성을 고려한 모니터링 지점이 필요하며, 이에 따른 정량적 산정식을 제안하는데 있다. 연구결과는 12개의 강우사상별 선정된 모니터링 지점은 거의 동일한 지점으로 나타났으며, 지점 선정의 결과는 모니터링 적합 방정식을 통해 정량적으로 표현할 수 있다. 그러나 본 연구는 대림3 빗물펌프장 유역만을 적용하였으며, 강우사상은 초과강우사상에 대한 결과를 나타내었다. 추가적으로 유량과 수질 내 변수의 최대값의 간격차이가 발생을 하여 이를 고려한 추가적인 연구가 필요할 것으로 판단한다. 본 연구에서 제시된 모니터링 적합 방정식은 우수관망 내 필요한 유출특성을 정량적으로 판단함으로써 현장의 의사결정자에게 모니터링 지점의 선정에 대한 판단 기준을 제공할 수 있다. 나아가 빗물펌프장을 비롯한 내배수시설의 효율적인 운영에 응용이 가능할 것으로 기대된다.
Acknowledgements
본 연구는 국토교통부 물관리연구사업의 연구비지원 (13AWMP-B066744-01)에 의해 수행되었습니다.