유공형 강판으로 전단 보강한 넓은 보의 전단강도 설계 규준 비교 분석
Comparison of Design Provisions on Shear Capacity for Wide Beams Reinforced Openings
Article information
Abstract
본 논문은 유공형 강판으로 전단 보강한 넓은 보의 전단파괴 실험을 수행하여 전단보강재의 전단성능을 평가하였다. 무보강 시험체와 유공형 강판으로 전단 보강된 총 11개의 시험체를 전단파괴 실험을 통해 계측한 전단강도와 KCI-12, CSA A23.3-04 설계규준의 전단식을 통해 얻은 전단강도와의 비교·평가하였다. 또한 보의 유효깊이, 횡방향 전단 보강재의 간격, 지지부의 폭을 변수로 하여 넓은 보의 전단강도에 미치는 영향을 분석하였다. 이를 통해 횡방향 전단 보강재의 간격이 줄어들수록 전단강도가 증가하고 지지부 폭이 줄어들수록 전단강도가 감소하는 것을 확인하였다.
Trans Abstract
In this paper, shear capacity of wide beam reinforced with steel plate with openings was evaluated. Three non-shear reinforced specimens and eight shear reinforced specimens were tested. Test results were compared with shear equations provided from the design provisions, KCI-12 and CS0A A23.3-04. Effective depth of beam, transverse spacing of shear reinforcement and width of support were considered as variables. Test results showed that the shear strength increased as the transverse spacing of shear reinforcements decreased while shear strength decreased as the width of support decreased.
1. 서론
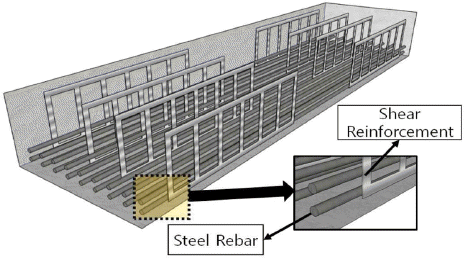
일반적으로 보의 폭이 보의 높이의 2배 이상인 보를 넓은 보로 분류한다. 넓은 보의 경우, 보 높이에 비해 보의 폭이 넓은 특징으로 인해 일반 보와 같이 철근 스터럽을 배치할 경우, 보의 바깥 측면에만 스터럽이 위치하여 횡방향 단면의 중앙부에 응력집중이 발생할 위험이 있다. 또한 대부분의 넓은 보의 폭이 기둥의 폭보다 크기 때문에 넓은 보의 폭 전체에 하중이 분포되지 않고 집중하중을 받을 수 있는 위험이 있다. 이러한 이유로 다수의 연구자들이 넓은 보에서 횡방향 전단보강재의 간격과 지지부 폭에 관한 연구를 수행하였다. Anderson et al. (1989)은 철근 스터럽의 형태 및 길이방향 철근과의 결속 방식, 그리고 배치 등을 변수로 실험을 수행하여 보의 전단성능을 평가하여 넓은 보에는 횡방향으로 다수의 전단보강을 하는 것이 전단성능을 향상시키는 방법임을 제안하였다. Lubell et al. (2008)은 넓은 보의 지지부 폭을 변수로 설정하여 지지부 폭이 증가할수록 전단성능이 증가하는 것을 실험을 통해 관찰하고 지지부 폭을 변수로 하는 전단강도의 감소계수를 제안하였다. 이와 같이 넓은 보에서 횡방향 전단 보강재의 간격과 지지부 폭이 전단성능에 영향을 미친다는 기존 연구결과에도 불구하고, 국내 콘크리트 설계기준인 KCI-12 (2012)와 캐나다 구조 설계기준인 CSA A23.3-04(2007)에서는 횡방향 전단 보강재의 간격과 지지부 폭에 대한 영향을 고려하지 않고 있다. 따라서 본 연구에서는 횡방향 전단 보강재의 간격과 지지부 폭이 전단강도에 미치는 영향을 평가하고, 실험을 통해 얻은 전단강도와 KCI-12와 CSA A23.3-04의 전단강도 식과의 비교를 통해 현재 규준에서 제시하는 전단강도의 설계식을 평가하고자 하였다. 또한 전단 보강재를 철근 스터럽으로 사용하지 않고, 기존연구(Choi et al., 2015)에서 제안한 유공형 강판을 전단보강재로 사용하였다. 유공형 강판으로 제작된 전단 보강재는 주철근에 끼우는 방식으로 설치가 용이한 장점이 있다. Fig. 1은 유공형 강판을 사용한 넓은 보의 대략적인 형상을 나타내었다. 유공형 전단 보강재는 개구부를 통해 콘크리트의 유동성을 증가시켜 부착력이 확보되고 철근에 비해 얇은 두께로 피복두께의 손실을 줄일 수 있다.
본 논문은 이러한 유공형 강판으로 전단보강한 넓은 보의 유효깊이, 횡방향 전단 보강재의 간격, 지지부 폭을 변수로 전단실험을 수행하였다. 이를 통해 넓은 보에 상기 언급된 변수들이 전단강도에 미치는 영향을 평가하고, KCI-12, CSA A23.3-04의 전단강도 설계식과 실험을 통한 넓은 보의 전단 강도를 비교·평가하는 것을 목적으로 하였다.
2. 설계 규준
2.1 KCI-12
KCI-12 설계식의 전단강도는 Eq. (1)에 나타낸 것처럼 콘크리트와 전단보강재의 전단강도 기여분의 합으로 구성된다. 본 실험은 넓은 보의 전단 파괴를 휨파괴보다 먼저 유도하기 위해 인장 철근비를 크게 설계하였다. 따라서 콘크리트 전단 강도 기여분은 인장철근비와 전단경간비가 변수로 포함된 Eq. (2)를 통해 계산하였다. 전단보강재의 전단강도 기여분은 KCI-12에 수록된 부재축에 직각인 단면철근을 사용하는 경우의 전단강도 기여분과 동일한 개념을 바탕으로 하여 Eq. (3)으로 계산하였고, 전단보강재의 단면적은 Eq. (4)를 통해 계산하였다.
2.2 CSA A23.3-04
CSA A23.3-04 기준식에서 콘크리트 보의 전단강도는 Vecchio et al. (1986)에 의한 수정압축장이론(modified compression field theory: MCFT)을 기반으로 산정되었다. 수정압축장이론은 균열 발생 후에 비균열 콘크리트 부분에 존재하는 인장지지능력을 압축장 이론에 추가하여 콘크리트의 전단 지지능력을 예측한 이론이다.
CSA A23.3-04 기준식의 전단강도를 산정하는 방법으로는 수정압축장이론을 간략화 시킨 simplified method와 보다 정 확한 값을 예측하고자 하는 general method가 있다(Bentz et al., 2006). Simplified method는 35º로 가정한 전단균열 경사각(θ)과 골재 맞물림 작용 계수(β)를 포함하여 전단강도를 계산한다. 하지만 simplified method는 인장철근의 항복강도가 400 MPa 이하일 때만 사용을 권장하고 있어서, 항복강도 500 MPa의 인장철근을 사용하는 본 연구에서는 general method를 사용하여 분석하였다. CSA A23.3-04 기준식의 전단강도는 Eq. (5)에 나타난 것처럼 콘크리트, 전단보강재, 프리스트레스의 전단강도 기여분의 합으로 구성된다. 본 연구에서는 프리스트레스가 포함되어있지 않기 때문에 이에 대한 기여분은 고려하지 않았다. 콘크리트의 전단강도 기여분은 general method에 의거하여 Eq. (6)을 사용하였다. 여기서 골재 맞물림 작용 계수는 Eq. (9)에 나타난 것처럼 인장철근의 변형률(εx)과 유효 균열 간격(sze)을 통해 구할 수 있다. 단, 유효 균열 간격은 규정에 의해 300의 값을 사용하였다. 전단 보강재의 전단강도 기여분은 Eq. (7)을 사용하였고, Eq. (8)을 통해 전단보강재의 단면적을 계산 하였다. 여기서 균열전단 각도는 Eq. (10)을 통해 구할 수 있고, 인장철근의 변형률은 Eq. (11)을 통해 구할 수 있다. 전단 보강재의 기여분에서도 콘크리트 기여분을 계산할 때와 마찬가지로 프리스트레스와 관련된 변수들은 고려하지 않았다.
3. 실험
3.1 사용 재료
시험체 제작에 사용된 콘크리트의 평균 압축강도는 KS F2405 (2009) 기준에 따라 재령 28일 후 압축강도 시험을 수행하여 계측한 결과, 평균 28.8 MPa임을 확인하였다. 인장철근은 지름 22 mm, 항복강도 500 MPa인 이형철근을 사용하였으며, 전단보강재인 유공형 강판의 항복강도는 402 MPa를 사용하였다. 실험에 사용된 재료의 물성치는 Table 1에 정리하였다.
3.2 시험체 상세
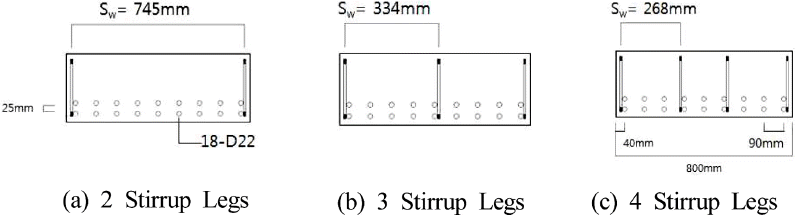
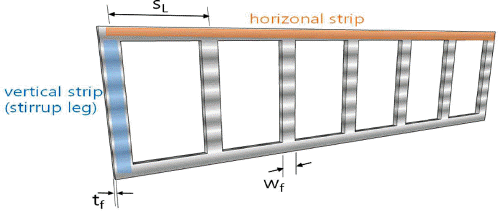
연구에 사용된 실험체는 유공형 강판으로 보강된 시험체 8개와 무보강 시험체 3개의, 총 11개의 시험체를 제작하였다. 시험체의 크기는 길이 3100 mm, 폭 800 mm, 높이 300 mm의 시험체 7개와 높이 340 mm, 380 mm의 시험체 각각 2개씩으로 구성하였다. 유효깊이는 240 mm, 280 mm, 320 mm로 설계하였다. 횡방향 전단 보강재의 간격은 전단보강재 사이의 중심거리로써 Fig. 2와 같이 268 mm, 334 mm, 745 mm 로 설정하였다. 여기서 유공형 강판의 항복강도와 단면적의 곱으로 산정되는 전단보강량(Av×fyt)은 동일하게 설계하였다. 유공형 전단보강재는 Fig. 3과 같이 수평과 수직 스트립으로 구성된다. 기존 연구(Kim et al., 2014)에서 판형태의 전단보강재에서 수평 스트립의 전단성능의 기여도는 매우 적어 세로 스트립만 전단 성능 기여분에 포함시킨다는 결과를 고려하여, 세로 스트립면적만 전단보강면적으로 산정하였다. 마지막으로 지지부 폭의 길이는 Fig. 4와 같이 800 mm, 600 mm, 400 mm, 200 mm로 설계하였다. 시험체의 상세는 Table 2에 정리하였다.
4. 실험 결과
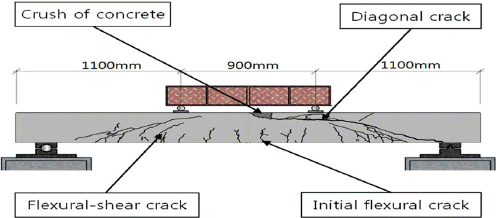
실험 결과 모든 시험체에서 Fig. 6에서 보여지는 것처럼 전단 압축파괴가 발생하였다. 초기균열은 보의 중앙부에서 휨균열이 발생 하였다. 이후 하중이 증가함에 따라 지지점으로부터 유효길이 만큼 떨어진 곳에서 휨 전단균열이 발생하였고, 이후 사인장 균열과 휨 전단균열이 증가하였다. 결과적으로 사인장 균열은 지지점 부근의 휨 전단균열과 연결되었다. 또한 가력지점 주변에 응력집중현상이 발생하여 해당 콘크리트 부분에 파쇄가 발생하였으며, 최종적으로 가력지점과 지지점을 연결하는 전단 균열에 의해 파괴되었다. Fig. 7에 시험체의 균열 및 파괴모드에 대한 균열도를 나타내었다. Table 3에는 모든 시험체의 최대 전단력(Vexp) 및 파괴모드를 정리하였다.
4.1 유효 깊이
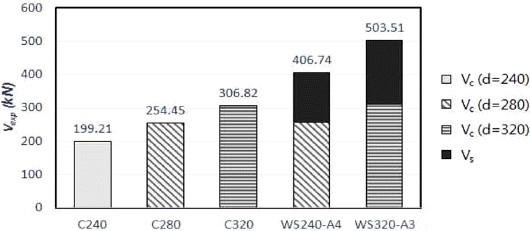
무보강 시험체인 C240, C280, C320 시험체의 경우, 유효깊이가 증가할수록 콘크리트 기여분의 전단강도가 증가하는 것을 알 수 있다. 또한 유공형 판으로 전단보강된 시험체 WS280-A3와 WS320-A3의 경우, 전단 보강량이 같음에도 불구하고 유효깊이가 증가할수록 전단보강재의 전단강도 기여분이 증가하는 것을 확인하였다. 따라서 본 연구를 통하여 유효깊이가 콘크리트와 전단보강재의 전단강도 기여분에 모두 관여함을 알 수 있다. Fig. 8은 실험을 통해 얻은 시험체의 전단강도를 그래프로 나타내었다.
4.2 횡방향 전단 보강재의 간격
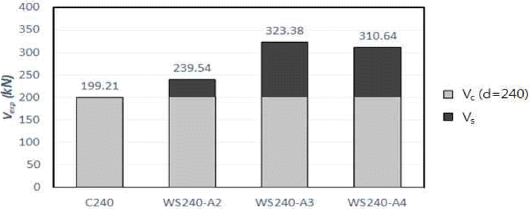
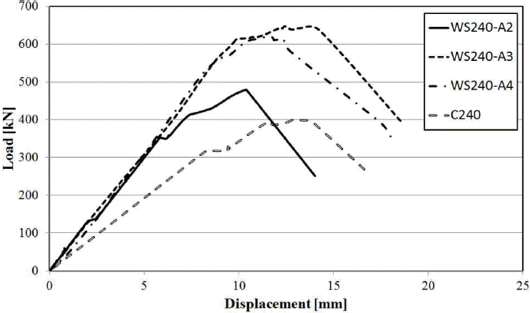
무보강 시험체인 C240의 전단최대하중 199.21 kN을 기준으로, 유공형 강판으로 전단보강된 시험체 WS240-A2, WS240-A3, WS240-A4의 최대 전단강도를 비교해 보았을 때, C240 시험체보다 각각 20%, 63%, 56% 증가된 전단보강 효과를 보였다. Fig. 9에 실험을 통해 계측한 전단강도를 그래프로 나타내었고, Fig. 10은 상기 언급된 시험체의 하중-변위 그래프를 나타내었다. 동일한 전단보강량에도 불구하고, 위의 세 시험체는 각기 다른 전단강도를 보였다. 이를 통해 동일한 전단보강량으로 보강하였어도 횡방향 전단 보강재의 간격에 따라 전단보강의 효과가 달라지는 것을 알 수 있다. 이는 간격이 줄어듬에 따라 보의 단면에 보강재의 레그수가 증가하여 응력집중현상을 감소시키는 것으로 판단된다. 하지만 횡방향 전단보강재의 레그 개수가 4개인 경우보다 3개인 시험체가 높은 전단강도에서 파괴된 것이 확인 되었다. 이는 Lubell et al.(2009)에서 규명한 것처럼, 다수의 스터럽 레그로 인하여 좁은 횡방향 전단 보강재의 간격이 형성되어 전단성능이 저하된 것으로 판단된다.
4.3 지지부 폭
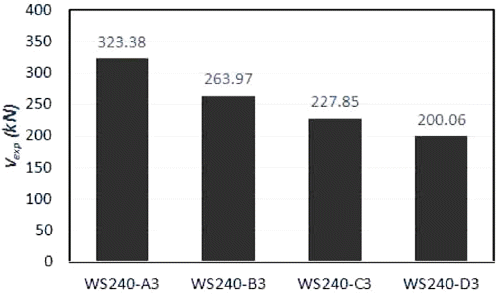
Fig. 11은 실험을 통해 계측된 WS240-A3, WS240-B3, WS240-C3, WS240-D3의 시험체의 전단강도를 나타내었고, Fig. 12는 위에서 언급된 시험체들의 하중-변위 그래프를 나타내었다. 시험체 WS240-A3를 기준으로 비교하였을 때, 시험체 WS240-B3, WS240-C3, WS240-D3은 WS240-A3 시험체의 전단강도 보다 각각 23%, 42%, 62% 줄어든 전단강도를 보였다. 이는 지지부 폭이 감소함에 따라, 지지부에 전단 압축응력이 집중되어 나타난 것으로 판단된다.
5. 설계 규준 비교
Table 4에 설계 규준을 비교하기 위해 시험체를 KCI-12와 CSA A23.3-04의 전단강도 설계식으로 계산된 전단강도와 실험을 통해 구한 전단강도를 정리하고, 두 값의 비인 전단강도비도 함께 나타내었다.
5.1 유효 깊이
유효깊이를 변수로하는 시험체 C240, C280, C320, WS280-A3, WS320-A3을 설계 규준들의 전단강도 설계식과 실험을 통해 계측한 전단강도를 비교해보았을 때, KCI-12은 평균 1.13, 분산 0.077로 나타났고, CSA A23.3-04는 평균 1.27, 분산 0.122로 나타났다. 결과적으로는 KCI-12가 CSA A23.3-04 보다 넓은 보의 전단강도를 산정할 때 더 정확하게 예측하는 것을 알 수 있다. 하지만 세부적으로 살펴보았을 때, CSA A23.3-04가 전단보강재의 전단강도 기여분은 더 정확하게 예측하고 있다. 이는 KCI-12에서는 전단균열각도를 45º로 설정하여 전단강도를 산정하지만, CSA A23.3-04에서는 수정압축장 이론을 적용한 결과에 따라 전단균열 경사각을 산정하기 때문이라고 판단된다.
5.2 횡방향 전단 보강재의 간격
횡방향 전단 보강재의 간격을 변수로 하는 시험체 WS240-A2, WS240-A3, WS240-A4를 전단강도 실험값과 각 코드의 전단강도 설계값을 비교해 보았다. 단 시험체 W240-A2는 CSA A23.3-04에서 간격을 600 mm 이하로 규정하고 있어, CSA A23.3-04의 계산에서 제외 하였다. KCI-12의 평균은 0.96, 분산은 0.12로 나타났고, CSA A23.3-04의 평균은 1.00, 분산은 0.02로 나타났다. 두 규준 모두 비교적 정확한 전단강도를 예측하고 있었지만, KCI-12규준의 경우는 CSA A23.3-04 규준처럼 전단보강재의 최대 간격을 규정되지 않아 시험체 WS240-A4에서 KC1-12 설계식이 실험값과 다소 큰 차이를 보였다. 이는 횡방향 전단 보강재의 간격이 크게 증가하였을 때, 전단강도를 과대평가 하게 되는 것을 알 수 있었다. 그리고 두 코드 모두 전단보강재의 최소 간격에 관한 규정이 존재하지 않고 있다.
5.3 지지부 폭
지지부 폭을 변수로 하는 시험체 WS240-A3, WS240-B3, WS240-C3, WS240-D3을 설계 규준을 통해 계산된 전단강도와 실험을 통해 계측된 전단강도를 비교해 보았을 때, 지지부의 폭이 넓은 보의 폭과 같은 경우 전단강도비는 각각 KCI-12은 1.06, CSA A23.3-04는 1.02로 비교적 정확한 전단강도를 예측하고 있었다. 하지만 두 규준 모두 지지부 폭이 넓은 보의 폭보다 작은 경우에는 감소된 전단강도를 예측하지 못하는 것을 확인하였다. 이를 통해 두 설계 규준 모두 지지부 폭에 대한 규정이 존재하지 않아 지지부 폭이 감소할 때, 정확한 전단강도를 예측하지 못하는 것을 알 수 있다.
6. 결론
본 논문에서는 실험을 통해, 강재로 제작한 유공형 판 형상의 전단보강재로 보강한 넓은 보의 전단성능을 평가하였다. 또한 KCI-12와 CSA A23.3-04의 전단강도 설계식을 통해 산정된 전단강도와 실험 결과를 비교 및 평가하였다. 이를 통해 얻은 결론은 다음과 같다.
(1) 유효 깊이가 증가할수록 넓은 보의 전단강도는 증가하며, 넓은 보에서 콘크리트와 전단 보강재의 전단강도 기여분에 모두 영향을 미치는 것을 실험을 통해 확인하였다.
(2) 전단보강재의 횡방향 간격이 증가할수록 전단강도가 감소하는 것을 확인할 수 있었다. 이는 간격이 증가하게 되면 넓은 보에 압축응력 집중현상 발생 때문인 것으로 판단된다.
(3) 지지부의 폭이 넓은 보의 폭보다 작을 경우, 전단강도가 감소하는 것을 확인하였다. 지지부 폭이 좁을 경우 보의 폭 전체에 하중이 분포되지 않고 집중하중을 받는 것을 확인 할 수 있었다
(4) KCI-12 규준의 경우 넓은 보의 전단강도 산정에 있어서, 횡방향 전단 보강재의 간격과 지지부 폭 감소에 의한 영향이 고려되지 않아 위의 변수에 대한 전단강도 측정에 있어서 정확한 값을 예측할 수 없었다.
(5) CSA A23.3-04 규준의 경우 횡보강 최대 간격에 대한 규정은 있으나, 최소 간격에 대한 규정이 없어 좁은 횡방향 전단 보강재의 간격으로 인하여 전단강도가 줄어드는 현상을 고려할 수 없다. 또한 지지부 폭에 대한 기준이 존재하지 않아, 지지부 폭이 보의 폭보다 작을 때 발생하는 하중 집중현상을 고려하지 못해 설계 전단강도보다 적은 전단강도가 발현될 가능성이 있다.
감사의 글
이 논문은 2011년도 정부(미래창조과학부)의 재원으로 한국 연구재단의 지원을 받아 수행된 연구임(NRF-2011-0016332).
Notation
Av
Sectional area of shear reinforcement (mm2)
As
Area of longitudinal reinforcement on the flexural tension side of the member (mm2)
a
Depth of equivalent rectangular stress block (mm)
bw
Width of wide beam (mm)
d
Effective depth of wide beam (mm)
dv
Effective shear depth of wide beam (mm)
Es
Modulus of elasticity of non-prestressed reinforcement (MPa)
Ep
Modulus of elasticity of prestressing tendon (MPa)
fck
Specified compressive strength of concrete by KCI-12 (MPa)
f’c
Specified compressive strength of concrete by CSA a23.3-04 (MPa)
fyt
Specified yield strength of shear reinforcement (MPa)
Nf
Factored axial load normal to cross section occurring simultaneously with Vf including effects of tendon due to creep and shrinkage, (kN)
Mf
Factored moment at a section (N·m)
sL
Center-to-center spacing of longitudinal shear reinforcement (mm)
sw
Maximal transverse spacing of longitudinal shear reinforcement (mm)
sze
Equivalent value of sz that allows for influence of aggregate size
Vc
Nominal shear strength provided by concrete (kN)
Vc,CSA
Nominal shear strength provided by concrete by CSA A23.3-04 (kN)
Vc,KCI
Nominal shear strength provided by concrete by KCI-12 (kN)
Vexp
Experimental maximum shear strength (kN)
Vf
Factored shear force at section (kN)
Vn
Nominal shear strength of wide beam (kN)
Vn,CSA
Nominal shear strength of wide beam by CSA A23.3-04 (kN)
Vn,KCI
Nominal shear strength of wide beam by KCI-12 (kN)