폭발위치에 따른 콘크리트 구조물의 접합부 형태별 구조거동 분석
The Structural Behavior of Concrete Structures by the Joint Types and Explosion Location
Article information
Abstract
구조물에서 발생하는 폭발사고 및 테러 등은 끔직한 재난으로 직결되곤 한다. 특히, 이러한 폭발 하중에 의해서 발생하는 구조물의 연쇄 붕괴 등은 수많은 인명피해를 야기해왔다. 따라서 폭발하중에 의한 구조물의 피해를 예상하고 대비하기 위한 기술의 정립이 필요할 것이다. 본 연구에서는 폭발하중을 받는 슬래브-기둥 접합부의 거동에 관한 연구를 해석적으로 수행하였다. 거동을 평가하기 위해서 내부기둥, 외부기둥, 모서리 기둥을 포함하는 구조물을 모델링 하였다. 해석 변수는 폭발하중의 위치로 설정하여 폭발하중의 위치에 따른 각 접합부의 거동 분석을 분석하였다. 해석 결과는 부재의 변위, 철근의 응력 등을 포함하고 있다.
Trans Abstract
The explosion accidents and terrorist attacks in the structures are directly connected to the horrible disaster. Particularly, the collapse of the structure caused by the explosive accidents has caused many casualties. Therefore, it is necessary to establish the technology to predict and prevent the damage of the structure due to the explosion load. In this study, the behavior of slab-column joint subjected to explosive load was analyzed. In order to evaluate the behavior of structures, the structure including interior columns, edge columns, and corner columns was modeled. The behavior of each slab-column type was analyzed according to the location of the explosive load, which is the main analytical variable. The analysis results include the deflections of the member, the stresses of the reinforcements, and so on.
1. 서론
폭발하중이 발생하는 구조물은 매우 짧은 시간에 높은 하중이 작용하기 때문에 높은 변형률 속도를 보이며 과다한 변형이 일어난다. 이러한 과다한 변형은 결국 파괴를 야기하여 재산 및 인명에 심각한 피해를 일으킬 것이며, 재산 및 인명을 보호하기 위해서는 특별히 안전한 설계가 수행되어야 한다. 특히, 구조시스템의 접합부는 발생하는 응력을 전달하는 등 매우 중요한 역할을 한다. 이러한 접합부는 응력의 불연속성이 존재하며 응력교란구역(D-region)으로 명시되며 접합부의 파괴는 전체 구조시스템의 붕괴를 야기하기 때문에 더욱더 안전한 설계가 수행되어야 할 것이다(Yoon, 2013; Park, 2011). 따라서 폭발하중을 받는 구조물 및 접합부의 피해를 예측하며 대비하기 위한 기술 구축이 필요할 것이다.
본 연구에서는 폭발하중을 받는 콘크리트 구조물의 거동에 대한 연구를 수행하였다. 대상 시험체는 접합부의 형태에 따른 내부기둥, 외부기둥, 및 모서리기둥-슬래브 접합부를 포함하는 구조물로 설정하였다. 해석 주요 변수는 폭발하중이 작용하는 위치로 설정하여 폭발의 위치에 따른 구조물의 거동을 해석적으로 분석하였다.
2. 방폭 구조물의 설계
2.1 방폭 구조물의 설계기준
불특정 다수를 대상으로 한 테러 및 예기치 못한 폭발사고에 대비하기 위해 전 세계적으로 방폭구조물의 설계에 대한 관심이 증가하고 있다. 특히 미국방부(DoD; Department of Defense)에서는 미육군, 미해군 및 미공군에서 보유한 테러대비 지침을 취합하여 UFC (Unified Facilities Criteria)를 2008년에 발표하였다(DoD, 2008). 다만 공개된 내용을 일부로 국한되어있으며 국가 안보와 밀접한 내용은 민간 열람에 어려움이 있다. 미국토목학회(ASCE: American Society of Civil Engineers)에서도 폭발하중을 받는 구조물의 등급을 평가하기 위한 기술을 확보하고 있다(ASCE/SEI, 2011).
국내에서는 국토해양부와 국방부에서 테러에 대비하기 위한 기준을 일부 제시하였으나 민간열람 가능한 내용은 상당히 일반적인 내용으로 구성되어 있는 수준이다(MND, 2009; MOLIT, 2010). 다만, 테러 및 폭발사고 등은 예기치 못한 시기에 예기치 못한 장소에서 발생하기 때문에 국가 주요 시설물 뿐만 아니라 민간차원에서도 이를 대비하기 위한 방책이 필요할 것이다. 따라서 국내 국가 주요 구조물 및 민간시설물에 적용하기 위한 방폭구조물의 설계 및 시공관련 연구가 충분히 수행되어야 할 것으로 판단된다.
2.2 방폭 구조물의 설계
폭발하중을 받는 구조물은 폭발하중에 저항하기 위한 충분한 연성과 에너지 흡수능력이 확보되어야 할 것이다. 높은 에너지 흡수능력과 보강철근으로 인한 연성으로 철근콘크리트구조물(RC)은 방폭구조물에 가장 일반적인 건설재료로 고려되어왔다(William, 2010; Dusenberry, 2010). 발전소와 같이 구조물처럼 방폭 성능이 요구되는 기존 구조물은 철근콘크리트 구조물로 설계되었으며 방폭성능 확보를 위해서 벽체의 두께를 비대하게 증가시키는 방법이 적용되어왔다. 다만 두께를 증가시키는 경우 자중의 증가, 사용공간의 감소, 시공비용의 증가 등 다양한 문제를 내포하고 있다. 다양한 시설물 및 구조물에 적용하기 위해서는 보다 효율적인 방폭 설계방법이 개발되어야 할 것이다.
콘크리트 구조물에서 접합부는 외부하중에 의해 발생하는 축력, 전단력, 비틀림 등 다양한 하중조합에 저항할 수 있도록 설계되어야 한다(Cormie et al., 2009). 이와 같은 하중조합에 저항하기 위한 효율적인 접합부의 설계방법으로는 일체형 접합부(monolithic joints)가 고려될 수 있다. 일체형 접합부에서는 다른 접합부의 형태보다 하중 전달능력이 높아 응력집중현상을 최소화 하며 전체 구조 시스템에 응력을 고르게 분포하여 안전성 향상을 기대할 수 있을 것이다(Dusenberry, 2010).
3. 콘크리트 구조물의 모델링
3.1 시험체 모델링
본 연구에서는 콘크리트 구조물의 방폭 성능을 해석적으로 평가하기 위해서 본 연구에서는 유한요소 해석프로그램 LS-DYNA를 사용하였다. LS-DYNA는 동하중과 같은 시간이력 해석을 위해 개발되었으며 특히, 충돌, 폭발과 같은 단기간에 높은 변형이 발생하는 해석에 특화되어 있다(LSTC, 2013b). 폭발하중을 받는 구조물의 거동을 분석하기 위해서, 본 연구에서는 Fig. 1과 같이 내부기둥, 모서리기둥 및 외부기둥을 갖는 구조물로 대상 시험체를 모델링 하였다. 사용된 콘크리트 재료모델은 Concrete damage model로 Mat_072R3을 사용하였다. 해당 콘크리트 재료모델은 높은 변형률 속도에서 다른 재료모델과 비교하여 실제 재료의 구현 정도가 더 높다고 알려져 있다(Crawford et al., 2012). 콘크리트 요소는 해석결과의 정확성 확보를 위해서 기존에 수행된 연구 및 타 연구자의 실험 및 해석 연구결과를 분석하여 20mm의 정방형의 Solid로 모델링하였다(Foglar and Kovar, 2013; Lim et al., 2016). 철근의 재료모델링을 위해 Mat_024를 beam요소에 적용하였으며 콘크리트와의 부착성 등 내부상호작용을 구현하기 위해 노드를 공유하는 방법이 적용되었다. 일반적으로 RC구조물의 해석에서 콘크리트와 철근의 부착, 정착과 같은 내부 현상을 모델링하는 것은 매우 중요하지만 폭발하중과 같이 높은 변형률 구간에서는 이러한 현상을 무시하는 것이 해석의 정확성을 향상시킨다는 기존의 문헌을 참고하였다(Crawford et al., 2012; Shi and Stewart, 2015).
폭발 및 충돌과 같은 동적해석은 시간이력해석으로 해석 대상 구조물이 거대해질수록 해석소요시간이 비대하게 증가한다. 따라서 유한요소해석에서 요소의 응력 및 변형 등을 계산하기 위하여 사용되는 방법 중 폭발해석에서는 주로 1점 적분법(1-point integration)이 사용되어왔다. 1점 적분법은 해석의 시간을 감소시킬 수 있으나 해석 시 가끔 0에너지상태(Zero-energy state)를 발생시킨다. 유한요소 해석에서 체적을 갖는 요소는 압력을 받으면 압력에 의해 체적이 감소하게 되어 내부 에너지에 변화가 생긴다. 반면, 1점적분법의 해석 오류로 인하여 0-에너지 상태가 발생하면 내부 에너지가 0이 되며 외부 내부압력이 오히려 체적을 팽창시키는 결과를 발생시킨다. 이러한 해석적 오류를 제어하기 위하여 ‘Hourglass control’이 요구된다(Kang and Oh, 1996; Kim et al., 2004). Hourglass 에너지의 발생량을 감소시켜 해석에 정확성을 보완할 수 있다. 본 연구에서도 이러한 해석적 오류를 제어하기 위하여 LS-DYNA에서 제공하는 Hourglass옵션을 적용하였다(LSTC, 2013a; Crawford et al., 2012).
3.2 폭발하중의 모델링
일반적으로 폭발하중을 모델링하기 위해서는 폭발물질을 Solid요소로 모델링 하며 요소에 TNT 등의 폭발물질의 재료적 특성을 입력하고 폭발조건을 설정하는 방법이 있다. 폭발물질을 Solid로 모델링 하는 경우 폭압을 구조물까지 전달하기 위하여 일반적으로 대기층이나 유체같은 전달체의 모델링이 필요하다. 이처럼 lagrangian요소로 모델링 되는 구조물과 eulerian요소로 모델링 되는 대기층에 대한 복합 요소 해석을 MM-ALE(Multi-material arbitrary lagrangian eulerian)이라고 부른다(Bae and Zakki, 2011; Tabatabaei and Volz, 2012). 이러한 해석 방법은 대기를 통해 전달되는 폭압의 흐름을 분석할 수 있으나 대기층의 모델링으로 인해 해석에 필요한 요소가 기하급수적으로 증가할 수도 있다. 시간이력해석에서 요소 수의 증가는 해석 소요시간을 비대하게 증가시켜 폭발해석에서 효율성을 상당히 저하시켜 왔다.
이러한 단점을 보완하기 위한 방법으로는 LS-DYNA는 폭발하중의 모델링 방법으로 LBE옵션(Load_Blast_Enhanced)을 제공하고 있다. LBE는 미육군 PDC(Protective Design Center)에서 개발된 ConWep(Conventional Weapons effects) 프로그램을 기반으로 하고 있다. LBE로 폭발하중을 정의하는 경우 설정한 TNT 폭약량에 따라 거리를 기준으로 발생하는 폭압을 요소에 직접적으로 작용시키게 설정되어있다(Huh et al., 2012; LSTC, 2013a). LBE옵션을 사용한 폭발해석은 앞서 언급된 MM-ALE방법에 비하여 해석시간을 상당히 절약할 수 있으며 해석결과의 차이가 크지 않은 장점이 있다. 따라서, 본 연구에서는 LBE를 활용하여 폭발하중을 정의 하였다.
3.3 폭발해석의 주요 변수
기존 타 연구자에 의한 연구 등에 의하면 정하중을 받는 기둥의 구속도에 따라 구조성능 차이가 발생함이 확인되었다(Bianchini et al., 1960; Gamble and Klinar, 1991). 본 연구는 폭발하중 조건에서 기둥의 구속도에 따른 구조거동을 비교하기 위하여 수행되었다. 해석 변수는 총 4가지로 구분하였으며 실험체의 구분은 Table 1과 같다. Case 1은 4개의 기둥 중앙, 즉, 슬래브의 중앙에 위치시켰다. Case 2는 내부기둥에 인접하게 작용시켰으며 Cases 3, 4는 각각 외부, 모서리 기둥에 인접하게 폭발하중을 위치시켰다. 여기서 내부기둥은 슬래브에 의해 4면이 모두 구속된 기둥을 의미하며 외부기둥 및 모서리기둥은 슬래브에 의하여 각각 3면 및 2면이 구속되어있는 형태의 기둥을 의미한다.
테러 공격에 의한 폭발물질의 등가질량에 대하여 유럽의 강구조학회에서는 Table 2를 제시하였다(Yandzio and Gough, 1999). 본 연구에서는 자전거를 사용한 폭발을 모델링하기 위하여 30kg의 TNT를 폭발하중에 적용시켰다.
4. 해석 결과 및 분석
4.1 유한요소 해석 결과 분석
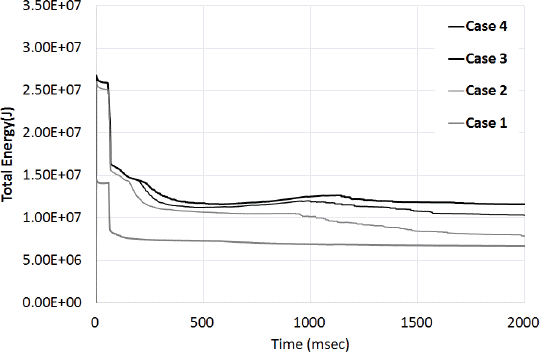
해석결과를 Fig. 2와 Table 3에 표기하였다. Fig. 2에서와 같이 모든 시험체에서 폭발에 의한 폭압이 구형을 나타내며 시험체에 작용하였다. 이러한 경향은 기존 문헌 등에서 언급된 폭압의 일반적인 형태로 폭발해석이 적절하게 수행되었음을 추측할 수 있을 것이다(DoD, 2008). Fig. 3에서 볼 수 있듯이 약 2,000 msec 이전에 전체 에너지가 수렴하였으며 안정을 찾았기 때문에 Table 3에서 언급된 바와 같이 해석 종료시간을 2,000 msec로 설정하였다.
Case 1의 경우 다른 시험체와는 다르게 폭발하중을 슬래브에 작용시켰기 때문에 전체 에너지가 적게 발생하였다. 이러한 경향을 미루어 볼 때 폭발하중이 단일부재에 작용하는 경우보다 접합부에 작용하는 경우 더 높은 에너지를 발생시킨다고 판단할 수 있을 것이다. 따라서 동일 하중조건에서 접합부는 단일 부재보다 더 큰 영향을 받는 것을 확인하였다. 또한 구속도가 가장 낮은 모서리 기둥과 밀접하게 폭발하중이 작용한 Case 4에서 내부에너지 및 운동에너지가 가장 크게 발생하고 있다. 따라서 기둥의 구속도가 폭발하중 저항능력에 영향을 미치는 것을 확인할 수 있을 것이다.
4.2 슬래브 거동분석
Fig. 4에는 각 부재의 슬래브 파괴형상을 나타내었다. 모든 시험체에서 배면의 파괴가 폭발하중을 직접적으로 받는 전면부에 비해서 더 크게 발생한 것을 확인할 수 있었다. 기존의 타 연구자들의 실험적인 연구에서도 폭발하중을 받는 전면부보다 배면에서의 파괴가 더 크게 발생한 경향을 확인할 수 있다(Foglar and Kovar, 2013; Thiagarajan et al., 2015). 따라서 본 연구에서의 폭발해석이 적절하게 수행되었다고 판단할 수 있을 것이다.
Case 1의 슬래브는 다른 시험체와 비교하여 기둥 부재와 거리가 있다. 즉, 지점 등에 의한 구속조건에 크게 영향을 받지 않기 때문에 Table 4의 슬래브 부재의 파괴 깊이 및 면적을 비교할 때 가장 큰 파괴면적을 보이고 있다.
Case 2, 3 및 4에서는 내부기둥, 외부기둥 그리고 모서리 기둥에 인접하여 폭발하중이 작용하고 있다. 기둥의 구속도가 높을수록 파괴 면적이 적게 발생하였으며 구속도가 가장 낮은 모서리기둥에서 폭발하중이 작용한 경우 파괴 면적이 가장 크게 발생하였다. 동일한 크기의 폭발하중이 모서리 기둥에서 작용하는 경우 구조물의 안전성이 취약해 진다는 것을 확인할 수 있다.
4.3 기둥의 거동분석
Case 1에서 폭발하중이 각 슬래브-기둥 접합부까지 영향을 미치지 못하였다. Fig. 4에서도 볼 수 있듯이 Case 1의 기둥은 피해를 입지 않았다.
Fig. 5는 Case 2, 3 및 4의 접합부 주위의 슬래브 및 기둥의 파괴 형상을 나타내고 있다. 또한 Table 5에서는 각 시험체의 폭발하중에 의한 기둥의 손상 정도를 비교하기 위해 파괴체적을 비교하였다. 해석 결과에서 볼 수 있듯이 앞서의 결과와 유사하게 모서리 기둥에서 가장 큰 파괴가 발생했음을 알 수 있다. 내부기둥에서는 상대적으로 파괴가 적게 발생하였다. 따라서 기둥의 구속도가 방폭성능에 영향을 미치는 것을
확인하였으며 외부 및 모서리기둥 접합부의 안전성 확보를 위해서는 적절한 조치가 필요할 것으로 판단된다.
5. 결론
본 연구에서는 기둥 슬래브로 설계된 구조물에 폭발하중이 작용하는 경우 폭발하중의 위치에 따른 구조물의 거동을 분석하고자 수행되었다. 구조물 거동을 파악하기 위해 해석적인 연구를 수행하였으며 연구결과를 다음과 같이 정리할 수 있다.
폭발하중이 작용하는 위치에 따라서 구조물에 발생하는 피해 정도에 차이가 있었다. 슬래브 중앙에 폭발하중이 작용하는 경우 슬래브 부재에 높은 손상을 일으키는 것을 확인하였다. 반면 접합부나 기둥에는 큰 피해를 일으키지 않았다.
슬래브에 의한 기둥의 구속도가 폭발하중의 저항능력에 영향을 미치는 것을 확인하였다. 내부기둥 접합부에 폭발하중이 작용한 경우 슬래브, 기둥 및 보강 철근에서 상대적으로 가장 적은 피해가 발생하였다. 반면 노출되어있는 면이 가장 많은 모서리 기둥에서는 모든 평가항목에서 가장 큰 파괴 및 피해가 발생하였다. 따라서 방폭 구조물의 설계를 위해서는 슬래브에 의한 기둥의 구속도를 고려하여 접합부의 종류에 따른 별도의 보강 방법이 적용되어야 할 것으로 판단된다.
본 연구를 바탕으로 폭발 하중이 발생하는 위치에 따른 위험 등급을 상대적으로 평가하면 다음과 같다. 슬래브 중앙에 발생하는 경우 상대적으로 피해가 적은 D, 내부기둥 접합부에 발생하는 경우 C, 외부기둥 접합부에 발생하는 경우 B, 그리고 모서리기둥 접합부에 작용하는 경우 가장 위험한 A로 평가할 수 있을 것이다. 이러한 연구결과를 바탕으로 하여 폭발하중의 크기, 부재의 보강 방법 및 보강 수준 등 다양한 변수의 검토가 병행된다면 국내 독자적인 방호등급 체계 구축에 기초자료로 활용 가능할 것으로 판단된다.