Elastic Buckling Assessment of Doubly Symmetric I-Beams with Singly Stepped Section at Midspan
Article information
Abstract
Over the years, several studies have been made for the improvement of the design criteria of stepped beams. However, studies on lateral-torsional buckling of stepped beams located at the midspan have been very limited. Hence, this study aims to evaluate the elastic lateral-torsional buckling strength of doubly symmetric singly stepped I-beam at midspan considering the load-height effect and various loading conditions. To model and perform the analysis for the I-beams, a universal finite element analysis program, ABAQUS, will be used. In addition, S4R elements will be used to model the simply supported beams where loads are applied at shear center and at top flange, and to check the accuracy of the models guide design specifications are used. The results from the finite element analysis will be shown using tables and illustrative figures. Based from the obtained results, conclusions and new design guidelines are proposed.
Trans Abstract
최근 스텝보의 설계기준 활용성을 향상시키기 위한 여러 연구가 진행된바 있다. 그러나 지간 중앙에 스텝단면이 보강된 I형보의 횡-비틀림 좌굴에 대한 연구는 제한적이었다. 본 연구는 지간 중앙에 스텝보가 적용된 I형보에 하중고 효과와 다양한 하중을 고려한 횡-비틀림 탄성좌굴강도를 평가하고자 한다. 범용유한요소해석 프로그램 ABAQUS가 사용되었으며, 쉘 요소인 S4R요소를 모델링에 적용되었고 해석결과는 기존 설계기준 및 기 발표된 제안식과도 비교분석 되었다. 본 논문은 다양한 표와 그림을 활용하여 해석결과를 나타내고 있으며, 해석연구 비교분석을 통하여 새로운 설계식 제안되었다.
1. Introduction
The cross section of continuous multi-span beams are sometimes suddenly increased, or stepped, at interior supports of continuous beams to resist high negative moment. However, sometimes in interior spans, the flanges are stepped at both the center of the span near maximum positive moment area and the supports at the negative moment areas which can be conservatively considered doubly stepped beam (Park and Kang, 2004). In fabrication of built-up weld beams, it is a common practice to use a constant web depth as well as flange width with increase in flange thickness to provide increased in moment of inertia. Stepped beams are either constructed by increasing the flange thickness of a welded beam or by welding additional flange plates to a hot-rolled I-section.
This paper presents an evaluation on the elastic lateral- torsional buckling (LTB) strength of doubly symmetric singly stepped I-beam at midspan considering the load-height effect. The loadings considered include cases with negative bending moments at both ends, a concentrated load, uniformly distributed load, and 2-point loading applied at shear center or at top flange. This research also presents new design equations that are similar to current lateral torsional buckling solutions which use a modifier to consider the effect of the change in cross section and to account for the varying moment along the unbraced length. The design equations were then compared with finite element analysis results.
2. Background and Previous Studies
Stepped beam was first introduced by Trahair and Kitipornchai (1971), they investigated the effects of steps in minor axis flexural rigidity, warping rigidity, as well as torsional rigidity. They have also studied the effects of the position of the steps on the lateral-torsional buckling strength of a simply supported beam with central concentrated loads. Although of its growing popularity, only few researchers have thoroughly studied on lateral-torsional buckling (LTB) of stepped beams. Park and Stallings (2003; 2005) wrote researches regarding lateral-torsional buckling strength of stepped beams at both ends. Park and Oh (2009) as well as Surla and Park (2014; 2015) also studied lateral-torsional buckling strength of monosymmetric stepped beams at both ends considering several loading conditions. Buckling strength of steel beams with random imperfections was also studied, in which Lellep and Kraav (2011) focused on the elastic buckling capacity of stepped beams having piece wise dimensions with cracks and Kala (2013) investigated the elastic lateral torsional buckling strength of steel I-beams with initial curvature and twist. Also, Mohebkhah and Chegeni (2012) wrote a research involving the nominal flexural capacity of I-beam sections having compact webs and noncompact or slender flanges taking into account the interaction between the lateral torsional buckling as well as the local buckling of the flange. Kulinski and Przybylski (2015) have studied the buckling strength of stepped beams resting on elastic foundation while Kucukler et al. (2015) research a stiffness reduction approach utilizing linear buckling analysis with developed stiffness reduction functions for the LTB assessment of stepped beams. Recently, Sadiqali and Krishnan (2017) conducted a research on the optimization of doubly and singly stepped I-beams for lateral torsional buckling subjected to transverse loading. Design equations for these stepped beams were presented to consider general loading cases, stepped conditions, load-height effect, and the effect of on lateral torsional buckling. Numerous design specifications have guides on how to determine the buckling strength of prismatic beams. Some of these specifications are AISC (2011), and AS 4100 (1998). The provisions of these specifications in calculating the buckling strength of prismatic beams were used in this study. To check the accuracy of the finite element model made, the values obtained using finite element analyses were compared with the values obtained using the mentioned specifications. The values calculated using AISC specifications were also used in comparing the strength of prismatic and stepped beams.
AISC (2010) specifications provide the following equation to calculate the elastic lateral torsional buckling capacity of doubly symmetric prismatic beams:
Where Cb is the moment gradient modifier, Lb is the unbraced length, E is the modulus of elasticity of steel, Iy is the moment of inertia of beam about Y-axis, G is the shear modulus of elasticity of steel, J is the St. Venant torsional constant for beam, and Cw is the warping constant of the cross section. Eq. (1) with Cb equal to 1 is the elastic lateral-torsional buckling resistance for an I-shaped prismatic section under the action of constant moment in the plane of the web over the laterally unbraced length (Timoshenko and Gere, 1961).
Moreover, the AISC (2011) and AASHTO LRFD (2010) have also incorporated the following equation as an expression for the moment gradient modifier, Cb, which is applicable for linear and nonlinear moment diagrams which is also based on the study of Kirby and Nethercot (1979) moment gradient factor, Cb, which takes into account the effect of varying moment depending on the loading condition is given as:
Where Mmax is the absolute value of maximum moment in the unbraced length, Lb, MA is the absolute value of moment at quarter point of the unbraced segment, MB is the absolute value of moment at centerline of the unbraced segment and Mc is the absolute value of moment at three-quarter point of the unbraced segment. There is no sign convention associated with Eq. (2); the absolute value is used for all moments. The loading is assumed to be applied at midheight of the cross section.
Ziemian (2010) presented the following equation for Cb for symmetric I-shaped girders subjected to transverse loading applied at different heights on the cross section:
Where A and B are taken from Table 1, the distance of applied load from midheight and beam depth. The distance is negative for loading applied above midheight, and positive for loading applied below midheight. However, the effects of load height and load condition can also be approximated by taking A equal to Cb in Eq. (2) and B equal to 1.4 (Helwig et al., 1997).
There are also studies made by Nawaz (2009) and Serna et al. (2006) for the equivalent uniform moment factors for lateral torsional buckling of steel beams which can be used as an alternative of the one given by AISC. However, for this study, the AISC (2011) and Ziemian (2010) are followed.
The high potential of stepped beams stems from its high strength while having lower self-weight than the prismatic beams having large cross-section all throughout. In opposition, the lack of specific design codes have been hindering the wider use of these type of beam. Comparison with different equations have been proposed in order to overcome the aforementioned limitations of stepped beams.
Previous studies that proposed equations that can be used for determining the elastic lateral-torsional buckling strength of doubly symmetric singly stepped I-beams were made by Park and Kang (2004), and Australian Standard AS 4100 (1998). The results from these equations were compared with the results of the finite element model to determine the equations’ safety and applicability. The equations used by Park (2004) in determining the elastic lateral-torsional buckling strength of doubly symmetric singly stepped I-beams at one end of the span are:
Where Most is the critical lateral-torsional buckling moment; Cst is the stepped beam correction factor for singly stepped beams; Cbst is moment gradient factor defined in Eq. (2) for shear center loading condition and as defined in Eq. (3) for top flange loading condition; Mocr is critical moment capacity of prismatic beam α; β, γ and are the ratios defining the relative length, relative width, and thickness of the large and small cross sections, respectively.
Similarly, the Australian code, AS 4100 (1998), have following equations in computing for the moment capacity of beams with segments fully or partially restrained at both ends:
Where Ms is the nominal section moment capacity; αm is the moment modification factor as tabulated in Table 2; αs is the slenderness reduction factor; and M0 is the reference buckling moment which is also equivalent to in Eq. (1) where Cb is equal to 1.
3. Finite Element Model
The finite element program, ABAQUS (2011), was chosen because of its wide material modeling capability and the program’s ability to be easily customized. A linear S4R element was chosen to model the beams due to its capability to provide enough degrees of freedom to clearly model the elastic buckling deformations of the beam. ABAQUS/CAE and ABAQUS/Standard were used in simulating the buckling behavior of the stepped beams when loading was applied and in determining the elastic buckling capacity of the stepped beams. The beams were analyzed as having an elastic behavior due to the fact that the unbraced length of 13.59 meters, 18.12 meters, and 22.65 meters were under the elastic range provided by AISC (2011).
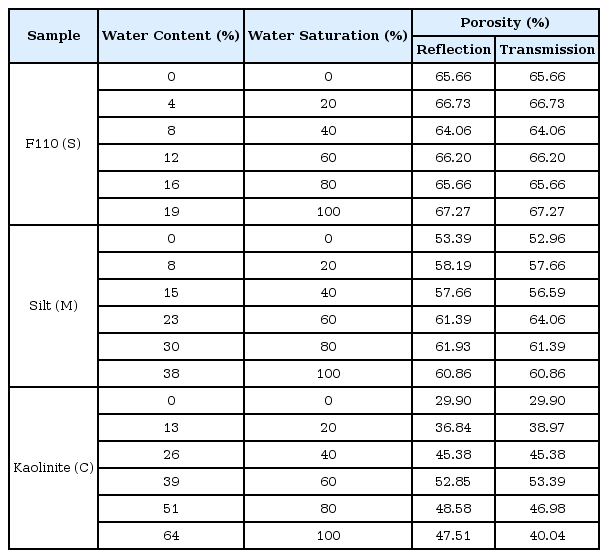
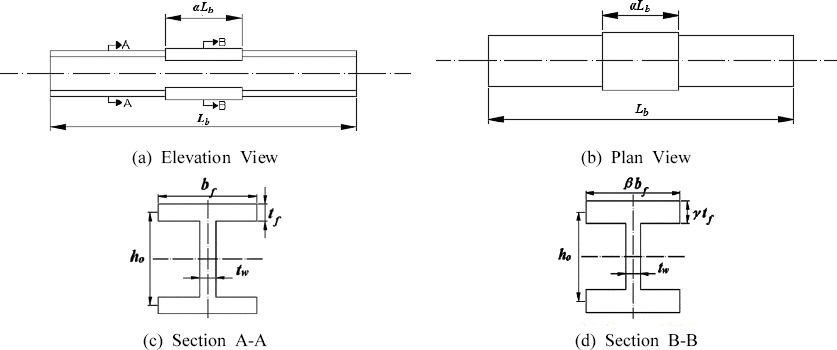
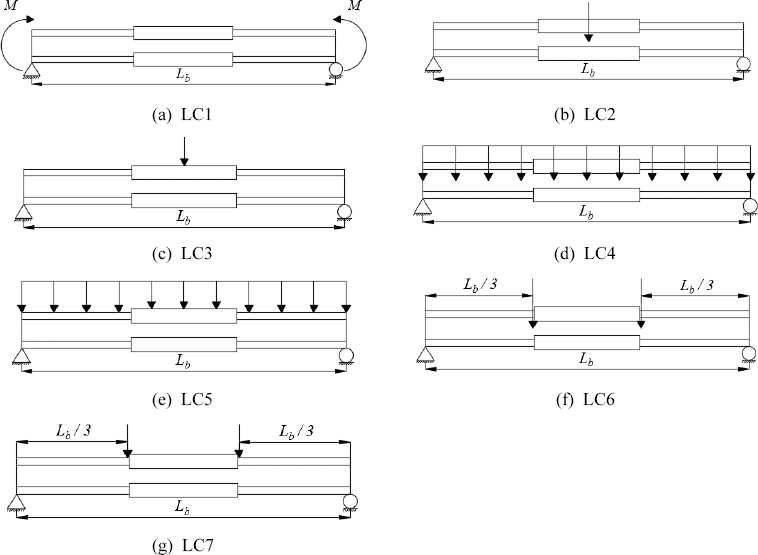
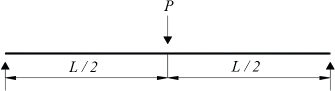
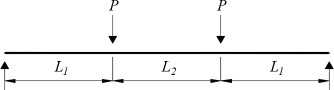
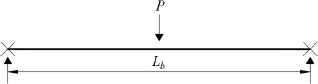
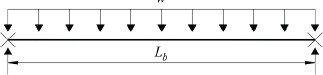
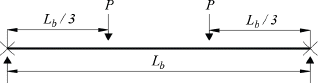
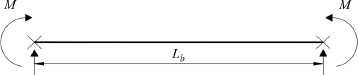
FEM eigenvalue analysis of 189 beam models were performed to develop a design equation for obtaining the LTB moment resistance of stepped beams. The study considered 27 cases of stepped beams parameters used by Park and Kang (2004). Fig. 1 shows the stepped beam parameters are α, β and γ with its elevation, plan, and cross sectional view. In addition, the values of the stepped beam parameters are summarized in Table 3. The beams used in this study are subjected to pure bending, and general loading conditions applied at shear center, and top flange as shown in Fig. 2. Fig. 3 shows the loading condition having positive end moment. Also, the beams has a simply supported boundary condition as shown in Fig. 4. The beam used for this study is a W36x256 I-beam with corresponding properties listed in Table 4.
4. Results
4.1 Beams Subjected to Pure Bending
Parametric analyses were conducted to determine the relationship between all the parameters discussed previously and the lateral torsional buckling strengths of I-beams. Singly stepped beams having 81 models with Lb of 13.59 m, 18.12 m, and 22.65 m were investigated. The buckling moment results from ABAQUS (2011) were used to compute the stepped beam correction factor, Cst, which is defined as the ratio between the moment capacity of the stepped beam and the buckling capacity of the prismatic beam having the smaller section subjected to pure bending. A statistical software, MINITAB 17 (2014), was used for developing new design equations.
The proposed elastic lateral torsional buckling equation for doubly symmetric I-beam with singly stepped at midspan subjected to pure bending is:
Where Most is the critical lateral-torsional buckling moment; Cst’ is the integrated stepped beam correction factor, Cst, from Eq. (5); Mocr is critical moment capacity of prismatic beam; α, β and γ are the ratios defining the relative length, relative width, and thickness of the large and small cross sections, respectively.
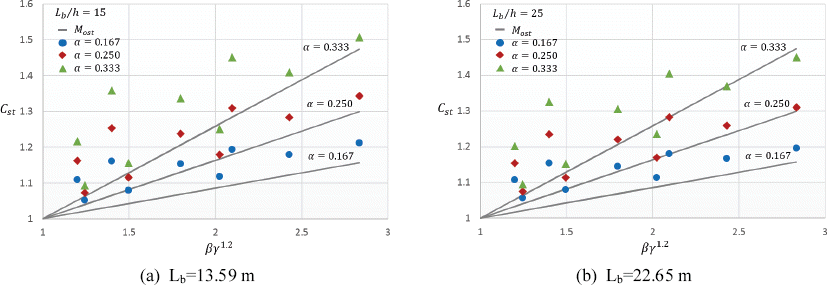
Fig. 5 presents the comparison between finite element model (FEM) and Eq. (5) for singly stepped beams at midspan with Lb/h of 15 and 25. The graph shows the straight lines with represents Eq. (5) with corresponding α values of 0.167, 0.250, and 0.333 while different shapes represents the FEM results. We can observe that FEM results provide a relatively upward and downward movement for the values of Cst as can be seen in Fig. 5.
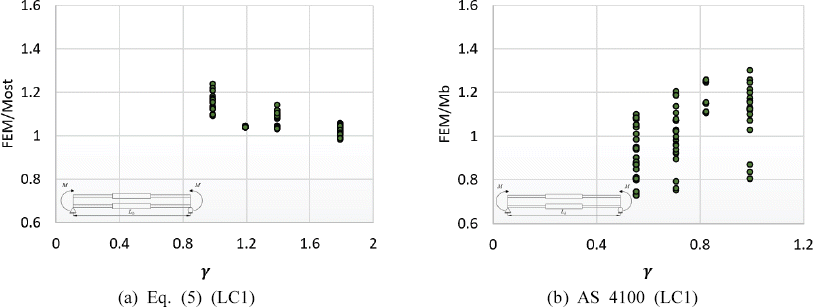
Fig. 6 provides comparison between FEM results, and those of Park’s and AS 4100 equations. In those figures, the ratio of the FEM result to that of those said equations are plotted against the value of gamma (γ) or the stepped ratio of flange thickness. If the value from each respective equations is exactly the same as the FEM result, the value on the vertical axis is equal to 1. The data below line 1 in the vertical axis indicate unconservative estimates with respect to FEM result. Based from Fig. 6(a), the maximum percentage difference for a conservative estimate of Eq. (5) is 18.77% at Lb/h=15 with α=0.333, β=1.4, and γ=1.0 while the maximum percentage difference for an unconservative estimate is -2.37% at Lb/h=25 with α=0.333, β=1.0, and γ=1.8. On the other hand, AS 4100 eq. provides fluctuating results with a maximum percentage difference for a conservative and unconservative estimate as high as 22.46% and -39% at Lb/h=15 with α=0.333, β=1.2, and γ=1.0 and at Lb/h=25 with α=0.25, β=1.4, and γ=1.8, respectively. These figures shows that the most of the estimates from AS 4100 were unconservative while Eq. (5) provides a more reasonable estimate for doubly symmetric beams with singly stepped at midspan under pure bending.
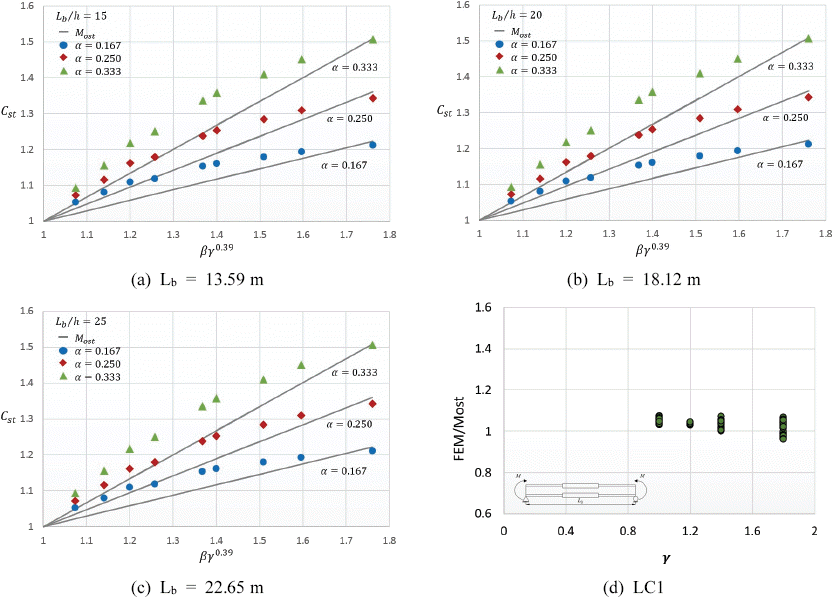
Fig. 7 provides comparison of LTB buckling strengths between FEM results and proposed equation. Figs. 7(a)-(c) shows that the results from FEM are almost in line with the trend of the proposed Eq. (9) which is different from those in Fig. 5 where the results have an upward and downward movement. In addition, we can observe that Cst is directly proportional to span-to-height ratio, meaning Cst increases as span-to-height ratio increases. Lastly, the proposed equation provides a maximum percentage difference for a conservative and unconservative estimate as low as 6.88% and -3.99% at Lb/h=15 with α=0.333, β=1.2, and γ= 1.0 and at Lb/h=25 with α=0.333, β=1.4, and γ= 1.8, respectively. Based from the results, we can say that the proposed equation gives the most conservative and reasonable results for doubly symmetric beams with singly stepped at midspan under pure bending out of the three design equations presented.
4.2 Beams Subjected to General Loading Condition
From the FEM investigation, the proposed design equation for elastic lateral torsional buckling strength of doubly symmetric I-beam with singly stepped at midspan subjected to general loading condition is:
Where Most is the critical lateral-torsional buckling moment; Cst’ is the integrated stepped beam correction factor as defined in Eq. (9); Cbst is moment gradient factor defined in Eq. (2) for shear center loading condition and as defined in Eq. (3) for top flange loading condition; Mocr is critical moment capacity of prismatic beam; α, β and γ are the ratios defining the relative length, relative width, and thickness of the large and small cross sections, respectively.
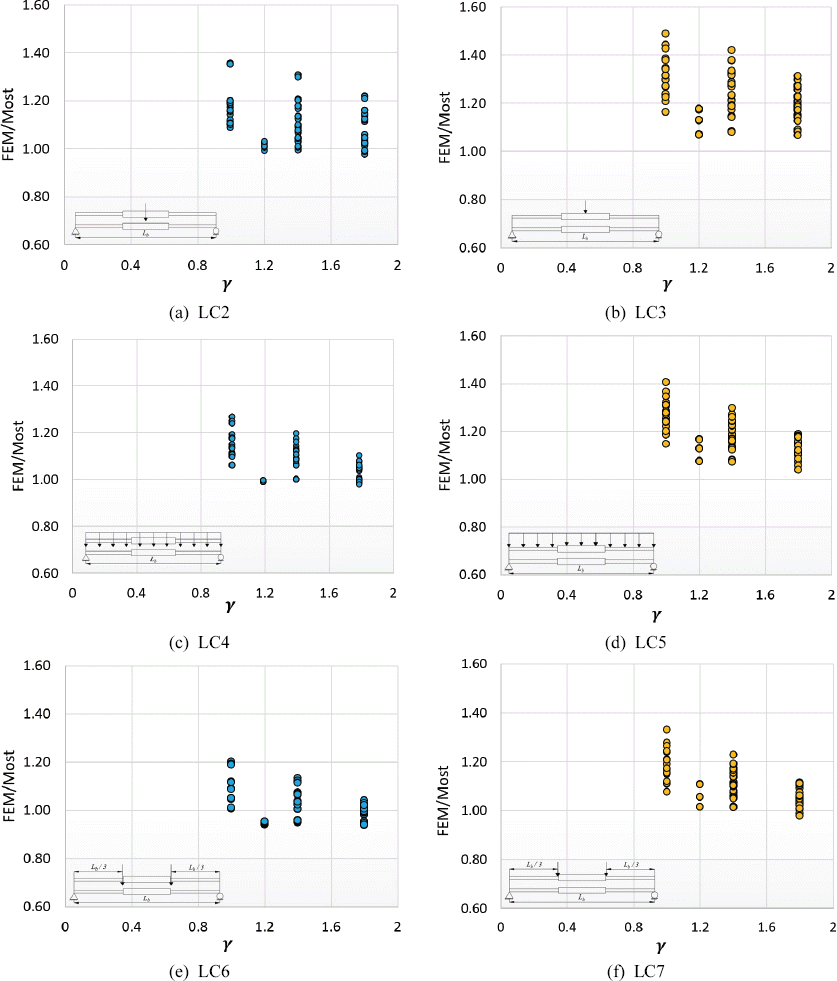
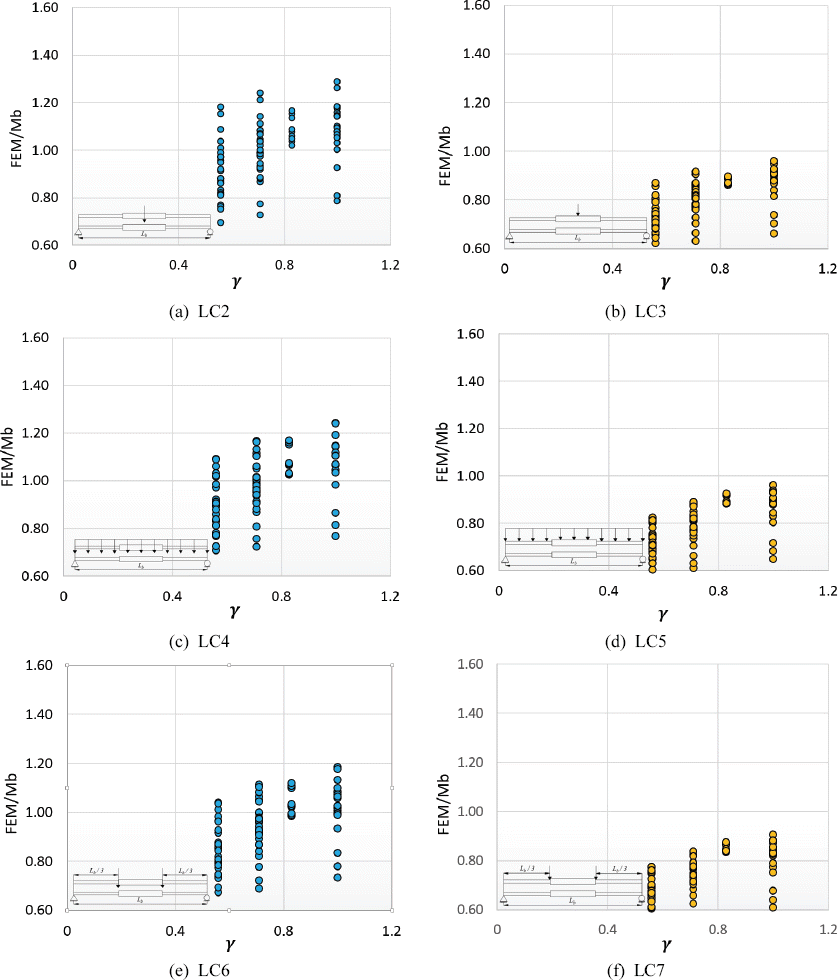
Load cases from LC2 to LC7 from Fig. 2 wereinvestigated for a simply supported stepped beams. The results of finite element method showed that Cb formula suggested by AISC (2011) in Eq. (2) and Ziemian (2010) in Eq. (3) can be used to determine the lateral-torsional buckling strength of a doubly symmetric I-beam with singly stepped at midspan subjected to pure bending or general loading conditions. Figs. 8-10 provides a comparison of lateral-torsional buckling strength between finite element method results and different equations for various load case scenarios shown in Figs. 1(b)-(g). Figs. (a), (c), and (e) from Figs. 8-10 shows cases of shear center loading while Figs. (b), (d), and (f) of Figs. 8-10 shows cases of top flange loading condition. In those figures, the ratio of the finite element method result to that of Eqs. (4), (6) and (10) are plotted against the value of gamma (γ) or the stepped ratio of flange thickness. If the value from each respective equations are exactly the same as the finite element method result, the value on the vertical axis is equal to 1. The data below line 1 in the vertical axis indicate unconservative estimates with respect to finite element method result.
Fig. 8 shows the comparison of lateral-torsional buckling strength between finite element model and Eq. (4) for beams subjected to general loading condition where loads are applied at shear center and top flange. These figures shows that top flange loading condition provide only conservative estimate for almost all cases. It also shows that shear center loading and top flange loading condition almost exhibit the same trend. It just differ in the range of accuracy. For shear center loading, the maximum difference of conservative estimate is 26.22% at Lb/h = 20 with α= 0.333, β= 1.4, and γ= 1 for beam subjected to concentrated while the maximum unconservative estimate is -6.55% at Lb/h = 15 with α= 0.333, β= 1, and γ= 1.8 for beam subjected to 2-point loading. On the other hand, the maximum difference of conservative estimate for top flange loading is 32.86% at Lb/h = 25 with α= 0.333, β= 1.4, and γ= 1 for beam subjected to concentrated while the maximum unconservative estimate is -2.19% at Lb/h = 15 with α = 0.333, β= 1, and γ= 1.8 for beam subjected to 2-point loading.
Fig. 9 shows the comparison of LTB strength between finite element model and Australian Standard Eq. (6) for beams subjected to general loading condition where loads are applied at shear center and top flange. It can be seen that for shear center loading condition (see Figs. 9(a), 9(c), and 9(e)), it provides a mixture of conservative and unconservative estimates. In addition, top flange loading provides the opposite results in Fig. 8 for it only gives unconservative estimate for all loading condition. For shear center loading, the maximum difference of conservative estimate is 22.41% at Lb/h = 15 with α= 0.333, β= 1.4, and γ= 1 for beam subjected to concentrated while the maximum unconservative estimate is -48.87% at Lb/h = 25 with α= 0.167, β= 1.4, and γ= 1.8 for beam subjected to 2-point loading. Alternatively, the maximum difference of unconservative estimate for top flange loading is -79.86% at Lb/h = 25 with α= 0.167, β= 1.4, and γ= 1.8 for beam subjected to 2-point loading.
Fig. 10 shows the comparison of LTB strength between FEM and proposed Eq. (10) for beams subjected to general loading condition where loads are applied at shear center and top flange. Similar with Park’s result, these figures shows that top flange loading condition provide conservative estimate for almost all cases. It also shows that shear center loading and top flange loading condition almost exhibit the same trend and just differ in the range of accuracy. For shear center loading, the maximum difference of conservative estimate is 16.62% at Lb/h = 15 with α= 0.333, β= 1.4, and γ= 1.4 for beam subjected to concentrated while the maximum unconservative estimate is -7.27% at Lb/h = 25 with α= 0.167, β= 1.4, and γ= 1.8 for beam subjected to 2-point loading. On the other hand, the maximum difference of conservative estimate for top flange loading is 23.27% at Lb/h = 25 with α= 0.333, β= 1.4, and γ= 1.4 for beam subjected to concentrated while the maximum unconservative estimate is -2.91% at Lb/h = 15 with α= 0.167, β= 1.4, and γ= 1.8 for beam subjected to 2-point loading.
Based from the results, the average percentage difference of shear center loading and top flange loading condition was 19.45%. In addition, it was concluded that beams where load was applied at the shear center have a higher strength compared to beams where load was applied at the top flange which was similar with the study of Morkhade and Gupta (2013). Also, estimates from Park’s, and proposed equation provided a more reasonable and conservative estimate compared to those of AS 4100 results which mostly gave unconservative estimate. Moreover, the difference of accuracy of Park’s and proposed equation can be evidently seen in cases where gamma was equal to 1 and 1.4. Lastly, the difference between the proposed solution and the FEM results was of -2.91% to 23.27% which was 10% less than those of Park’s results. This findings were drawn for cases of singly stepped beams at midspan subjected to general loading conditions such as uniformly distributed load, a concentrated load, or a series of concentrated load.
5. Conclusions
This research presents the elastic lateral torsional buckling strengths of doubly symmetric I-beam with singly stepped at midspan subjected to pure bending and general loading conditions. A finite element program ABAQUS (2011) was used for the parametric analysis. In addition, three design equations were considered for the computation of lateral-t orsional buckling capacity of stepped I-beams. After analyzing the results, the following conclusions were made. First, the Cst value was directly proportional to span-to-height ratio, meaning increases as span-to-height ratio increases. Second, the Cb formula suggested by AISC (2011) can be used for doubly stepped beams with singly stepped at midspan subjected to pure bending or general loading conditions. Third, top flange loading produced more conservative estimate compared to shear center loading condition. However, cases with shear center loading condition provided a closer range of accuracy. Lastly, the proposed equations for determining the lateral-torsional buckling resistance of doubly symmetric I-beams with singly stepped at midspan provided a percentage error with range of -2.91% to 23.27%. However, improvements and further study can be made which can include inelastic analysis and experimental tests to verify the drawn conclusions.
Acknowledgement
This research is supported by the Korean Ministry of Education, Science and Technology (NRF2015-059692) and Technology Advancement Research Program (17CTAP- C132629-01) funded by Ministry of Land, Transportation and Maritime Affairs of the Korean Government.