2.1 연구 대상 및 전략

Fig. 1에서와 같이 본 연구의 대상이 되는 소화탄 모델은 두 가지이다(National forest Research Institute, 2016). H-E(Highly Explosive) type과 Pyro type인데, 전자는 화약(gun powder)이 채워져 있는 분산 폭관(distributed explosive tube)에 전기로 점화를 하는 반면, 후자는 화약 덩어리로 둘러싼 스퀴브(squib)로 점화를 한다. 따라서 일단 폭발이 일어나면, H-E type은 원통형(cylindrical; 2차원) 모양, Pyro type은 구형(spherical; 3차원) 모양의 충격파가 발생한다.

Fig. 1

Two Types of Fire Extinguishing Bombs

Fig. 2는 이러한 문제의 풀이 전략을 개념적으로 나타낸 것이다. Fig. 1의 폭탄 구조와 같이 먼저 수중 충격파의 전파를 경화 기체 모델의 일종인 Saurel and LeMetyer(2001) 모델과 Sedov(1959)의 상사 이론을 사용하여 모델링한다. 즉, 본 문제를 이상 유동의 1차원 충격파관 문제로 단순화하고, Sedov 이론으로 다차원 감쇠를 모델링한다. 최종적으로는 소화액의 동역학 모델을 만들어 액적의 속도와 비산 거리를 구할 수 있다.

Fig. 2

Strategy for the Solution of Model in the Present Problem

2.2 예비실험 및 결과

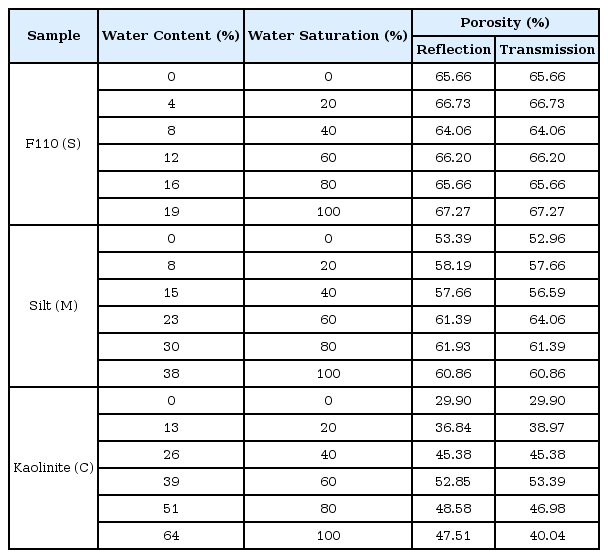
국립산림과학원에서는 Fig. 1 모델의 실험을 통하여 대략의 비산 거리를 측정한 바 있다. 폭발의 영향 영역이 얼마인지 측정하는 일은 쉽지 않다. 폭발원으로부터 거리에 따라 지면에 종이를 깔아 놓고 충분히 젖었을 경우 소화액이 비산된 것으로 판단한다. 측정 데이터는 Table 1에 정리되어 있다(National forest Research Institute, 2016). 소화액의 비산 거리는 시료에 따라 약 7~10 m로 측정된다.

Table 1

Preliminary Experiment for the Fire Distinguishing Bombs

2.3 1차원 이상 유동 충격파관 문제

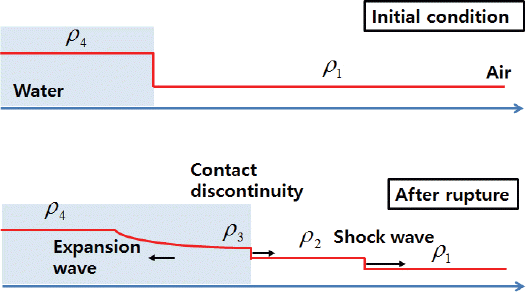
Fig. 3에서는 1차원 충격파관(shock tube) 문제의 개념도를 보여준다. 현재의 문제가 교과서적인 충격파관 문제와 다른 점은 고압부(driver section)가 물로 채워져 있다는 점이다. 여기에서 접촉 불연속면(contact discontinuity)은 물과 공기의 경계면(interface)이 된다. 충격파(shock)는 경계면에 선행하여 공기 중을 전파하며, 이에 대한 반작용으로 팽창파(expansion wave)가 물속에서 중심을 향하여 전파될 것이다. 실제로 Fig. 1의 모델에서 화약 부위는 물속에 있지 않지만, 편의상 고압부의 매질은 물이라고 가정한다.

Fig. 3

Schematic Diagram for the One Dimensional Two-phase Shock Tube Problem

1차원 충격파는 본질적으로 불연속 초기치가 주어진 Riemann 문제로 볼 수 있다. 폭발의 반경 방향으로 이러한 1차원 충격파관 문제를 풀이한다. 이 때 고압부의 초기 압력은 p₄, 저압부의 압력은 대기압과 같은 p₁으로 주어진다. 각 매질의 비열비는 각각 γ₁(공기)과γ₄(물)로 주어진다.

충격파의 전후 압력비(p₂/p₁)에 대해 이동 충격파 마하수(Mach number, M_s)는 공기 중에서 다음과 같이 주어진다(Anderson, 1992).

물과 공기의 경계면인 접촉 불연속면의 전파 속도(u_p)는 대기의 음속(speed of sound, a₁)에 대하여 다음과 같이 표현된다. 충격파 후에 유도되는 유동 속도(u₂=u₃) 역시 이 전파 속도와 같다. 접촉 불연속면 전후로는 압력도 같다(p₂=p₃).

Eqs. (1), (2)는 일반적인 기체역학(gas dynamics) 문제에서와 동일하다. 그러나 물을 매질로 할 때는 경화 기체 모델을 사용한다. 음속과 상태 방정식(equation of states)은 Fig. 3의 3~4 구간에 대해 다음과 같이 주어진다(Flåtten et al., 2011).

여기에서 c_v, c_p는 각각 정적 비열과 정압 비열을 의미하며(비열비는γ=c_p/c_v), a, e는 각각 음속과 단위 질량당 내부 에너지(internal energy), 그리고 p, ρ, T는 각각 압력(pressure), 밀도(density), 온도(temperature)를 의미한다. 고압부에서의 비열비와 오프셋 압력 값은 다음과 같다(Saurel and LeMetayer, 2001).

등엔트로피(isentropic) 구간인 팽창파 내부에서는 Riemann 불변량(invariant)을 고려하여 특성 곡선법(method of characteristics)을 적용하면, 최종적으로 다음과 같은 관계식을 얻는다. 특히 폭발 초기 조건에서 u₄ ≠ 0인 관계를 가정한다(Anderson, 1992).

Eq. (8)에서 초기 조건으로 주어진 p₄/p₁로부터 p₂/p₁값을 구할 수 있다. 여기에서 공기에 대하여 γ=1.4, 그리고 상온에서의 표준 값인 a₁=340m/s(공기)와 a₂=1,481m/s (물)를 사용한다(Greenspan and Tschiegg, 1957).

최종적인 계산 결과는 Fig. 4에 제시되어 있다. 수중에서는 수10만 이상의 압력 비가 작용하며, 초기 압력 비 1.15×10⁵에서, 1차원 입자 속도는 600 m/s에 이른다. 비록 실험 조건이 다르지만, 이는 90 m 거리에서 측정된 초기 유동 속도가 600 m/s 정도라는 러시아 ASP-500 대규모 실험 결과와 비교할 수 있는 수준이다(National forest Research Institute, 2016).

Fig. 4

Mach Number, Strength of Shock Wave and Particle Velocity for the Given Initial Pressure Ratio

2.4 다차원 감쇠 이론

Sedov의 상사 이론(Sedov, 1959)을 적용하면, 원기둥(2차원) 혹은 구(3차원) 모양의 대칭 파동에 대하여 충격파 이후의 압력(p₂)과 유동 속도(u₂)를 구할 수 있다.

Eq. (10)에서 E₀는 초기 폭발의 총 에너지이며, η는 충격파로 전달되는 에너지의 효율(0<η<1), 그리고 l은 분산 폭관의 길이에 해당한다. Eqs. (11)~(12)는 수중에서의 전파식이며, 비열비는 Eq. (6)에서의 값(γ₄)을 이용한다.

충격파가 r₂=R(폭탄 내벽의 반경 위치)에 이르렀을 때, 벽면에서의 충격파 반사를 고려하지 않는다면 벽면을 격막(diaphragm)과 같이 순간적으로 파쇄 시킬 수 있다. 따라서 Eqs. (11)~(12)에서 초기 상태에 대하여 p₄≈p₂, u₄≈u₂로 놓고, Fig. 3과 같은 새로운 Riemann 문제를 구성할 수 있다. 이를 정리하면, 다음과 같다.

원통형의 경우(v=2):

구형의 경우(v=3):

Eq. (14)에서 구형파의 경우 벽면에 완전히 압력을 가할 때까지 약간의 차이가 존재하므로, 0<ε<0.5인 값을 사용한다.

Eqs. (13)~(14)를 초기 조건으로 앞 절에서와 같이 풀면, 초기 u_p=u₂=u₃값을 계산할 수 있으며, 이 값으로부터 감쇠되는 속도는 상사 이론으로부터 다음과 같이 구할 수 있다(Chang and Han, 2010).

2.5 운동 방정식

Eq. (15)는 비산되는 액적의 반경 방향 속도를 나타내지만, 실제 유체는 중력(gravity)의 영향을 받기 때문에 경로에서 손실이 일어난다. 이러한 아이디어는 Fig. 5의 개념도로써 주어진다. 반경 r인 원 안을 휩쓸고 지나가는 소화액의 질량 유량을 m˙이라고 표시하면, 아주 작은 반경 차이인 dr에 대하여 변하는 질량 유량인 dm˙의 미분 방정식을 만들 수 있다.

Fig. 5

Conceptual Drawing for the Mass Loss

다차원 감쇠 과정에서 물과 공기의 경계면은 Fig. 3에서와 같이 깨끗하지 않고, 3번 영역(접촉 불연속면과 팽창파 사이)의 매질은 파형이 팽창하면서 물과 공기의 혼합물로 구성된다. 따라서 공극률(void fraction, α)의 개념을 사용한다.

여기에서 ρ_α는 공기의 밀도를 의미한다(ρ_l⪢ρ_α). 공극률은 다음과 같은 모델을 구성한다.

Eq. (18)의 경계 조건(boundary condition)은 r=R에서는 α=0(물)이고, r→ ∞에서 α=1(공기)이다.

액적에 대한 연속 방정식(continuity equation)을 Eq. (16)의 양변을 적분하여 구성하고, 여기에 Eqs. (15), (17)을 적용하면,

Eq. (19)가 항상 음의 값(질량 유량의 손실)을 갖기 위해서는, R/r<1이므로, 다음 부등식을 만족시켜야 한다.

Eq. (19)를 무차원 꼴로 정리하면, 다음과 같은 무차원 분포 함수(distribution function)를 만들 수 있다.

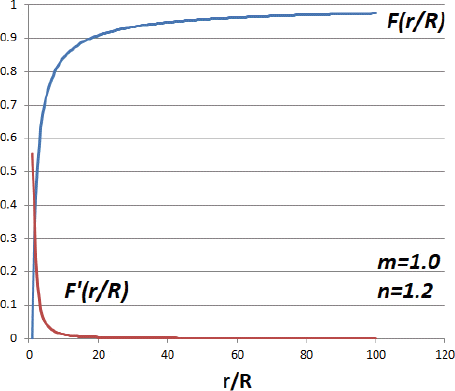
Eq. (21)은 해당 반경 내에 누적된(accumulated) 액적의 분포와 상사하기 때문에, 이를 무차원 반경 위치(r/R)에 대해 미분한 값은 손실된 액적의 질량 유량 분포와 상사한 것으로 추정된다.

3.1 파라미터 튜닝

Eq. (22)에서는 두 개의 차수가 존재한다. 이상 유동의 분포를 나타내는 m값과, 다차원 값을 나타내는 n값이 있다. 이들을 선택하는 데는 어느 정도 임의성이 존재하지만, 각각 Eqs. (15)와 (20)의 범위 안에 있어야 상사해가 존재한다.

Fig. 6의 사진은 예비 실험 결과로서, 차원의 감쇠가 2차원(n=1)도 3차원(n=1.5)도 아닌 그 중간에 있다는 것을 물리 현상으로 보여준다. 2.4절에서의 전제인 대칭 및 자기 유사(self-similarity) 조건은 실제 물리 현상과는 상당한 차이가 있다. 그럼에도 불구하고 평균적인 소화액의 비산량 분포는 ‘적분 효과(integration effect)’로 인하여 1차원 파동 역학과 다차원 상사성 감쇠 이론을 따른다고 가정한다. 본 연구에서 사용한 파라미터 값은 다음과 같다.

Fig. 6

The Pattern of Explosion for the First Case in Table 1

Eq. (23)에서 n을 일종의 형상 계수(shape factor)로 볼 수 있으며, 이 값이 작을수록 2차원에, 클수록 3차원에 가까운 폭발파의 형상을 보인다. 반면 m은 액적의 분포를 조정하며, 이 값이 클수록 폭발 지점 근방에 소화액이 집중되는 효과가 있다. 이 두 파라미터를 적당히 조정해 가면서 Table 1 실험 데이터와의 비교를 실시하였다. Fig. 7은 #1 실험을 n=1.2, m=1로 조정한 결과이다. 약 55%의 액적이 폭발 위치(r/R=1)에 집중되어 있다.

Fig. 7

Accumulation and Distribution of the Water Droplets for Given Dimensionless Radii

3.2 이론의 적용

Table 2는 Table 1의 세 실험의 조건으로부터, 본 문제의 모델에 적합한 입력 파라미터 조건을 나타낸 것이다. C4 폭약에 대해서는 기존 문헌의 연구 데이터를 참조하여 TNT의 1.34배로 폭발 에너지를 정하였으며(US Head Quaters in Dept. of Army, 1984), Pyro 폭약의 경우 정확한 데이터는 없지만 대략 C4의 75%로 추정한다. 전달 효율(η)은, 종이 케이스의 경우 95%, 나무 케이스의 경우 파쇄에 필요한 에너지를 고려하여 90%로 추정한다.

Table 2

Experimental Conditions for Parameters

3.3 계산 결과

Table 3은 2장에서의 이론을 실험 데이터에 적용하여 계산된 결과를 정리한 것으로, 여기에서 u_10m는 =10 m에서의 감쇠된 속도이다. 파형이 3차원 구형에 더 가까운 #3 실험의 경우, 초기 액적 속도(u₄≈u_p) 값이 나머지 실험에서 보다 크지만, 차원 상사성에 대한 감쇠로 인하여 반경 10 m 위치에서는 상당 부분 감쇠함을 알 수 있다.

Table 3

Computed Result of Each Case

액적의 수직 낙하 속도는 파동에 비해 훨씬 느리고, 중력과 주변 공기의 항력에 의한 종단 속도(terminal velocity)로 매우 느리게 떨어진다고 볼 수 있다. 즉, 액적의 분포는 Eq. (22)와 기하학적으로 상사하다고 생각한다. 2.2절 예비 실험 결과를 이용하여, 영향 영역(effective region)을 단위 면적 당 10 g(10 ml)만큼 물이 뿌려졌을 때 인지할 수 있는 것으로 가정하였다.

여기에서 초기 M₀=20kg질량 으로 모든 경우 동일하다.

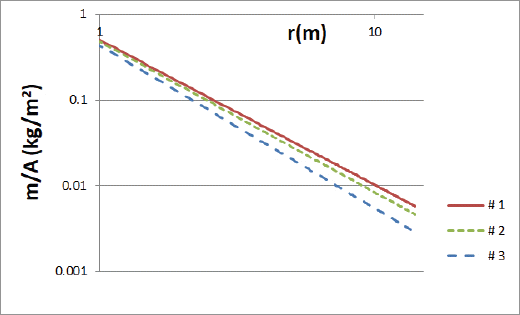
Eq. (24)의 해로 주어지는 r≤r_eff를 구하여 Table 1의 실험 결과와 대응시키는 방법으로 파라미터 (m, n)을 구했으며, 이들은 Table 3에 함께 제시되어 있다. Fig. 8은 3개의 실험 케이스에 대해서 각각 거리에 따른 질량 분포를 로그 스케일로 보여준다.

Fig. 8

Mass Distribution for Water Droplets in the Three Cases of Experiment

Table 3을 살펴보면, 이상 유동의 분포 파라미터 m은, 탄체의 재질이 종이보다는 나무이거나 또는 분산 폭관보다 점원(point source)의 점화계를 이용한 경우에 수평보다 수직 방향의 유동 전달이 상대적으로 더 크기 때문에 더 큰 값을 가져야 한다. 파형의 형상 파라미터인 n은, #1~2의 경우 좀더 1(2차원)에 가까운 값을, #3에 대해서는 1.5(3차원)에 가까운 값을 가져야 할 것이다. 본 연구에서는 전자의 경우 n=1.2를, 후자의 경우 n=1.4를 사용하였다.

초기 방사속도 u_p와 형상 파라미터 n이 주어졌을 때, 현재의 데이터로부터 선형 내삽(linear interpolation)을 이용하여 다음과 같은 상관관계(correlation)를 제시할 수 있다.

3.4 폭발 높이의 영향

앞 절의 이론은 무한한 영역의 매질에 대하여 완전한 대칭을 가정하고 원통 혹은 구면파를 가정하고 풀이한 것이다. 그러나 Fig. 6과 같은 실제 상황에서는 폭발 높이와 지면 효과(ground effect)의 영향을 무시할 수 없다.

Fig. 9에서는 이러한 높이 효과의 개념을 보여주고 있다. 충격파의 강도에 대해서는 1차원 이론의 경우 반사 충격파에 대해서 다음과 같은 식이 성립한다(Anderson, 2003).

Fig. 9

Shock Reflection from the Ground

여기에서 M_R은 강체(rigid body)인 지면에서 반사되는 이론적인 반사 충격파 마하수이다.

반사된 충격파의 영향으로, 접촉 불연속면 이후 물 영역의 기하학적 형상은 변형될 것이며, 특히 수직 방향으로의 역류하는 유량을 증가시킬 것이다. Fig. 6의 관찰에서도 위 방향으로 큰 물기둥이 발생하는데, 이 사실을 뒷받침한다. 수직 방향 반사 충격파에 의해 유도되는 부가 압력의 영향으로 소방수의 층은 약간 더 얇아지고, Eq. (25)에서 형상 계수는 다음과 같이 수정된다.

여기에서 σ_R은 지면에서의 충격파 반사에 의하여 부가되는 형상 파라미터로서 실제 값은 거의 1에 가까울 것으로 보인다. 즉, 반사 충격파의 영향은 폭발파의 파형을 좀 더 납작하게 만들어 원통형(n=1)에 가깝게 만든다(Eq. (15) 참조).

3.5 이론의 한계

실험 데이터의 부족으로 본 연구에서 개발한 상사 이론은 통계적으로 유의미한 확인(validation)을 거치지는 못했다. 그러나 제시된 구간에서의 실험값을 미리 예측하는 데는 매우 유용하게 사용할 수 있다.

실제 소화탄에 이론의 적용에는 분명히 한계가 있다. 본 연구의 이론에서 미처 고려하지 못한 사항들은 다음과 같다:

이러한 이론의 한계는 추후 실험과 해석을 계속하여 보완해 나가야 할 것이다. 현재 국립산림과학원에서는 관련된 후속 연구를 기획하고 있다. 전산유체역학(CFD)과 같은 직접 해석법을 도입하는 것도 대안 중의 하나일 것이다.

실제 화재에 소화탄을 적용하는 데에는 매우 세심한 주의가 요구된다. 일반적으로 소화탄은 밀폐 공간에서의 화재에 더 효과적이다. 산림화재와 같이 개방된 공간에서의 방재는 화재 단계별 바람의 영향 등에 의해 매우 어렵다.