1. ņä£ļĪĀ
2. ņŻ╝ņä▒ļČä ļČäņäØĻ│╝ ļĪ£ņ¦ĆņŖżĒŗ▒ ĒÜīĻĘĆļ¬©ĒśĢ
2.1 ņŻ╝ņä▒ļČä ļČäņäØ
2.2 ļĪ£ņ¦ĆņŖżĒŗ▒ ĒÜīĻĘĆļ¬©ĒśĢņØä ņØ┤ņÜ®ĒĢ£ ņ¦æļŗ©ļČäļźś
3. ļīĆņāüņ¦ĆņŚŁ ņäĀņĀĢ ļ░Å ņ×ÉļŻī ĻĄ¼ņČĢ
3.1 ļīĆņāü ņ¦ĆņŚŁ ņäĀņĀĢ
3.2 ņóģņåŹļ│Ćņłś ņé░ņĀĢ
3.3 ņäżļ¬ģļ│Ćņłś ņé░ņĀĢ
4. ĒśĖņÜ░Ēö╝ĒĢ┤ ņśłņĖĪĒĢ©ņłś Ļ░£ļ░£ ļ░Å ņśłņĖĪļĀź ĒÅēĻ░Ć
4.1 ņŻ╝ņä▒ļČä ļČäņäØņØä ĒåĄĒĢ£ ņäżļ¬ģļ│Ćņłś ļ│ĆĒÖś
Table┬Ā2
| Test | Result | |
|---|---|---|
| KMO test | 0.944 | |
| BartlettŌĆÖs test of Sphericity | Approx. Chi-Square | 54683.630 |
| Degree of freedom | 465 | |
| P-Value | 0.000 | |
Table┬Ā3
Table┬Ā4
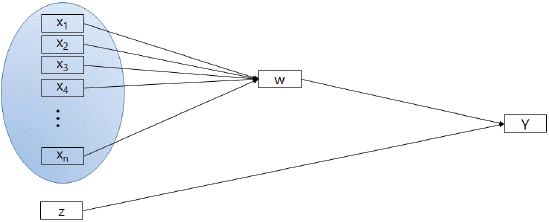
4.2 ļĪ£ņ¦ĆņŖżĒŗ▒ ĒÜīĻĘĆļ¬©ĒśĢņØä ņØ┤ņÜ®ĒĢ£ ņ¦æļŗ©ļČäļźś
(3)
(4)
(5)
4.3 ņśłņĖĪļĀź ĒÅēĻ░Ć
Table┬Ā5
4.4 ņĄ£ņóģ ļ¬©ĒśĢ ņĀ£ņŗ£
Table┬Ā6
5. Ļ▓░ļĪĀ
(1) ĒśĖņÜ░Ēö╝ĒĢ┤ ņśłņĖĪĒĢ©ņłśņØś ņóģņåŹļ│ĆņłśļĪ£ 2005ļģäļČĆĒä░ 2015ļģäĻ╣īņ¦Ć ņŗ£ĻĄ░ĻĄ¼ļ│ä/ņ×¼ĒĢ┤ĻĖ░Ļ░äļ│ä ĒśĖņÜ░Ēö╝ĒĢ┤ ņ×ÉļŻīļź╝ ņé¼ņÜ®ĒĢśņśĆĻ│Ā, ņØ┤ļź╝ ļĪ£ņ¦ĆņŖżĒŗ▒ ĒÜīĻĘĆļ¬©ĒśĢņØä ņØ┤ņÜ®ĒĢśņŚ¼ Ēö╝ĒĢ┤ņĢĪņØ┤ Ēü░ ņ¦æļŗ©Ļ│╝ ņ×æņØĆ ņ¦æļŗ©ņ£╝ļĪ£ ļČäļźśĒĢśņśĆļŗż.
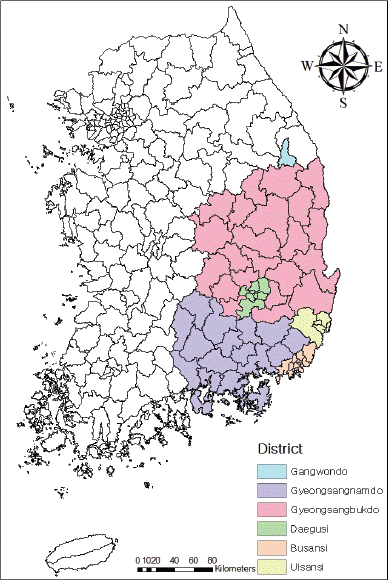
(2) ņäżļ¬ģļ│ĆņłśļĪ£ ņäĀĒ¢ēĻ░ĢņÜ░ļ¤ē(1~7ņØ╝), ņ┤Ø Ļ░ĢņÜ░ļ¤ē, ņ¦ĆņåŹņŗ£Ļ░äļ│ä ņĄ£ļīĆĻ░ĢņÜ░ļ¤ē(1~24ņŗ£Ļ░ä), ņ×¼ĒĢ┤ņØ╝ņłś, ņŗ£ĻĄ░ĻĄ¼ļ│ä ļ®┤ņĀüņØä ņé¼ņÜ®ĒĢśņśĆĻ│Ā, ņāüĻ┤Ćņä▒ņØ┤ Ļ░ĢĒĢ£ ņäĀĒ¢ēĻ░ĢņÜ░ļ¤ēĻ│╝ ņ¦ĆņåŹņŗ£Ļ░äļ│ä ņĄ£ļīĆĻ░ĢņÜ░ļ¤ēņŚÉ ļīĆĒĢ£ ņŻ╝ņä▒ļČä ļČäņäØņØä ņŗżņŗ£ĒĢśņŚ¼ ņāłļĪ£ņÜ┤ ņäżļ¬ģļ│Ćņłśļź╝ ļÅäņČ£ĒĢśņśĆļŗż.
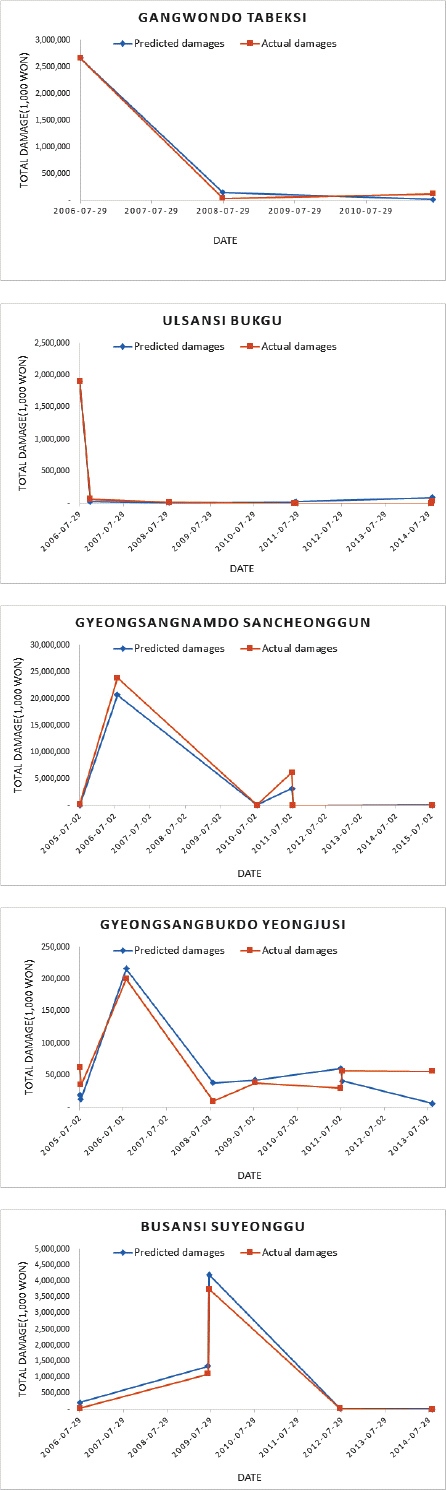
(3) 2005~2012ļģäņØś ļ│Ćņłśļź╝ ņØ┤ņÜ®ĒĢśņŚ¼ ĒśĖņÜ░Ēö╝ĒĢ┤ ņśłņĖĪĒĢ©ņłśļź╝ Ļ░£ļ░£ĒĢśņśĆĻ│Ā, Ļ░£ļ░£ļÉ£ ĒĢ©ņłśņØś ņä▒ļŖźņØä Ļ▓Ćņ”ØĒĢśĻĖ░ ņ£äĒĢ┤ 2013~2015ļģäņØś ņŗżņĀ£ Ēö╝ĒĢ┤ņĢĪĻ│╝ ļ¬©ņØśļÉ£ Ēö╝ĒĢ┤ņĢĪņØä ļ╣äĻĄÉĒĢśņŚ¼ ņśłņĖĪļĀźņØä ĒÅēĻ░ĆĒĢśņśĆļŗż.
(4) NRMSE Ļ░ÆņØä ņĄ£ņåīļĪ£ ĒĢśļŖö Ēö╝ĒĢ┤ņĢĪ ļČäņ£äņłś 75%ņŚÉņä£ ņĄ£ņĀüņØś Ļ▓ĮĻ│äĻ░ÆņØ┤ ņäĀņĀĢļÉśņŚłĻ│Ā, ņØ┤ļĢīņØś NRMSEļŖö 12.44%ļĪ£ ļéÖļÅÖĻ░Ģ ĻČīņŚŁņØś 69Ļ░£ ņŗ£ĻĄ░ĻĄ¼ņØś ĒśĖņÜ░Ēö╝ĒĢ┤ļź╝ ņĀüņĀłĒĢśĻ▓ī ņśłņĖĪĒĢśļŖö Ļ▓āņ£╝ļĪ£ ĒīÉļŗ©ĒĢśņśĆļŗż.
(5) ņäĀĒ¢ē ņŚ░ĻĄ¼ļōżņŚÉņä£ļŖö Ēö╝ĒĢ┤ņĢĪņØ┤ Ēü░ ĒśäņāüņØä ņĀüņĀłĒĢśĻ▓ī ļ¬©ņØśĒĢśņ¦Ć ļ¬╗Ē¢łļŖöļŹ░, ļ│Ė ņŚ░ĻĄ¼Ļ▓░Ļ│╝ņŚÉņä£ļŖö Ēö╝ĒĢ┤ņĢĪņØ┤ ņ×æņØĆ ņé¼ļĪĆ ņÖĖņŚÉ Ēö╝ĒĢ┤ņĢĪņØ┤ Ēü░ ņé¼ļĪĆņŚÉņä£ļÅä ņĀüņĀłĒĢśĻ▓ī ņśłņĖĪĒĢśļŖö Ļ▓āņ£╝ļĪ£ ļéśĒāĆļéś ĻĖ░ņĪ┤ņØś ļ¼ĖņĀ£ņĀÉņØä ĒĢ┤Ļ▓░ĒĢśļŖöļŹ░ ļÅäņøĆņØ┤ ļÉ£ Ļ▓āņ£╝ļĪ£ ĒīÉļŗ©ļÉ£ļŗż.