가법모형과 Double Penalty Approach를 이용한 가뭄지수 예측
Drought Index Forecast Using an Additive Model and the Double Penalty Approach
Article information
Abstract
가뭄의 심도와 빈도가 강해지는 상황에서 가뭄예측을 위한 연구가 지속적으로 이루어지고 있으나 가뭄현상의 시간적 변동 특성이 비선형 형태로 가지고 있어 가뭄예측개선을 위한 다양한 방법의 적용이 이루어지고 있음에도 불구하고 개선의 여지가 많은 상황이다. 본 논문에서는 기상가뭄지수인 표준강수지수 SPI와 세계기후지수와 같은 다양한 설명변수들 사이의 비선형 관계를 보다 잘 설명하는 평활스플라인(Smoothing Spline) 함수와 가법모형(Additive Model)을 적용하여 가뭄예측모형을 구성하였다. 과대적합문제를 해결하기 위해 변수선택법인 Double Penalty Approach(DPA)를 이용하여 가뭄 지수 예측을 개선하였으며 장기 강우자료가 가용한 서울, 인천, 대구, 추풍령, 제주, 목포, 강릉 총 7개 지점에 적용하여 모형 적합성을 분석하였다. 분석결과 모든 지점에 대하여 DPA 이용하여 변수선택 후 가법모형을 적용한 경우가 가장 좋은 결과를 보였다.
Trans Abstract
In a situation of the severity and frequency of drought events getting stronger, researches related drought forecast were conduced to improve the forecast accuracy. However nonlinear characteristics of temporal behavior of drought events leave us a large room to improve the drought forecast. For better modeling the non-linear relationship between the meteorological drought index SPI (Standardized Precipitation Index) and other independent variables such as world climate indices, we build a more flexible additive model using a smoothing spline function. Also, in order to get more accurate drought prediction, we applied a variable selection method, especially Double Penalty Approach (DPA) for resolving the over fitting problem caused by the additive model application. Applicability of the model was analyzed by appling the model for several sites, Seoul, Incheon, Daegu, Chupungrung, Jaeju, Mokpo, and Gangrung, which have long term rainfall data. Results demonstrated that the additive model with DPA generated better forecasts than other approaches at all sites.
1. 서론
자연재해와 관련하여 인류가 해결해야하는 도전적 과제 중 하나가 가뭄에 대응하는 것이다. 가뭄은 강수량의 부족으로 인해 발생하는 자연 재해로써, 장기간에 걸쳐 넓은 지역에 대하여 수많은 사람들에게 인명피해뿐만 아니라 경제적 피해를 야기한다. 국내외적으로 가뭄예측관련 연구는 많이 수행되고 있으며 Bordi et al. (2005)은 autoregressive (AR)모형과 Gamma Highest Probability(GAHP) 방법의 표준강수지수의 예측성을 비교하여 GAHP방법이 전형적인 AR모형보다 예측성이 뛰어남을 보였다. Cancelliere et al. (2007)은 자기공분산함수를 이용하여 가뭄의 등급별 예측전환확률을 예측하는 모형을 개발하여 과거 강수자료를 이용하여 표준강수지수의 예측성을 개선하는 방법을 제시하였다. Hwang and Carbone(2009)은 조건부 재 샘플링 기법을 적용하여 선행시간 1개월에 대한 표준강수지수의 예측을 개선하는 방법을 제시하였다. Hannaford et al. (2011)은 공간 일관성(coherence) 패턴을 이용하여 영국의 표준강수지수 예측을 개선하는 방법을 제시하였다. DeChant and Moradkhani(2015)는 가뭄 회복 예측의 민감성에 대한 분석을 통하여 가뭄예측 정확도가 지면 초기조건의 정확한 정보가 중요함을 보였다. Bonaccorso et al. (2015)은 표준강수지수와 기후지수의 하나인 North Atlantic Oscillation Index를 사용하여 이탈리아 시실리 지역의 가뭄 등급전환 확률예측에 있어 표준강수지수 단일 자료를 사용한 예측보다 개선됨을 보였다. 국내에서도 Rhee(2015)은 위성 및 장기예측자료를 활용하여 기계학습의 적용을 통한 가뭄예측의 개선 가능성을 제시하였으며 앙상블 기법, 신경망 기법 등 각종 통계 및 수학기법을 적용한 가뭄변동특성 분석과 예측성 향상을 위한 연구가 수행되었다(Kwon et al., 2009; Bae et al., 2012; Lee et al., 2016).
우리나라에서도 가뭄극복을 위하여 관련 연구뿐만 아니라 여러 부서에서 가뭄감시 및 조기 경보 시스템을 구축하여 운영하고 있으며, 기상청은 가뭄정보센터를 설립하여 여러 가뭄지수의 현황과 예측 정보를 제공해 왔고, 소방방재청은 국가 가뭄재해정보시스템 개발 사업을 수행하였으며 한국수자원공사에서는 국가가뭄정보분석센터를 설립하여 운영 중이며, 한국농어촌공사는 농업가뭄평가시스템을 운영하고 있다. 이러한 노력에도 불구하고 가뭄 피해를 최소화시킬 수 있는 보다 정확한 가뭄예측 정보의 제공은 도전적인 과제로 남아있다. 그러므로 본 논문의 목적은 기상학적 가뭄의 심도를 나타내는 표준강수지수(Standardized Precipitation Index, SPI)에 대한 가뭄 예측을 개선하는 것으로 비선형성이 강한 가뭄자료의 시간변동특성과 설명변수와의 상관관계에 대한 설명력을 높이기 위하여 평활스플라인(Smoothing Spline)함수를 활용한 가법모형(Additive Model)을 적합시키고 최적 모형 구축을 위한 변수선택방법인 Double Penalty Approach(DPA)을 이용하여 영향을 주지 않는 변수들을 제거하여 모형을 개선하였다. 개발 모형은 장기 강수자료가 가용한 7개 지역(서울, 인천, 대구, 추풍령, 제주, 목포, 강릉)의 표준강수지수 예측에 적용하여 모형 적합성을 분석하였다.
2. 자료 및 방법
2.1 입력자료
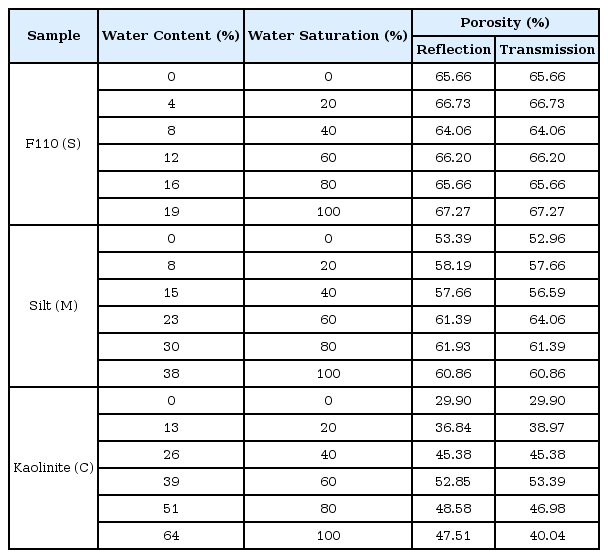
본 연구에서 세계기상기구(WMO: World Meteorological Organization)에서 가뭄감시를 위한 주변수로 선택한 표준강수지수를 통하여 가뭄예측을 수행하였으며 사용된 자료는 1954년부터 2015년까지 각 지역별로 표준강수지수, 기온, 강수량, 강수일수 그리고 세계기후지수들로 구성되어 있다. 대상기간에 강수자료가 가용한 서울, 인천, 대구, 추풍령, 제주, 목포, 강릉 총 7개 지점에 대하여 가뭄예측모형을 적합시켰다. Table 1은 세계기후지수로 SOI(Southern Oscillation Index), MEI(Multivariate ENSO Index) 등 본 연구에서 사용된 총 23개의 지수를 나타낸다.
Input Data of World Climate Indices
본 분석에서는 현재 시점에 대한 각 지역의 표준강수지수를 종속변수로 두고, 한 달 전과 두 달 전의 각 지역별로 표준강수지수, 기온, 강수량, 강수일수, 그리고 세계기후지수를 각각 설명변수로 두는 경우(Lag1, Lag2), 포함해서 설명변수로 두는 경우(Lag1+2) 이렇게 3가지의 경우에 대해 선형회귀모형과 가법모형을 구축하여 가뭄 예측성을 비교하였다. McKee et al. (1995)은 양수는 풍수기를 나타내고 음수는 강수부족을 나타내는 표준강수지수를 여러 단계로 구분하여 가뭄의 정도를 나타내었다. Table 2에는 7개 단계로 표현한 표준강수지수의 가뭄의 심도의 구분표로 지수가 -1 이하일 때 일반적으로 가뭄이 시작하는 것으로 판단한다.
Classification of Drought Severity for SPI
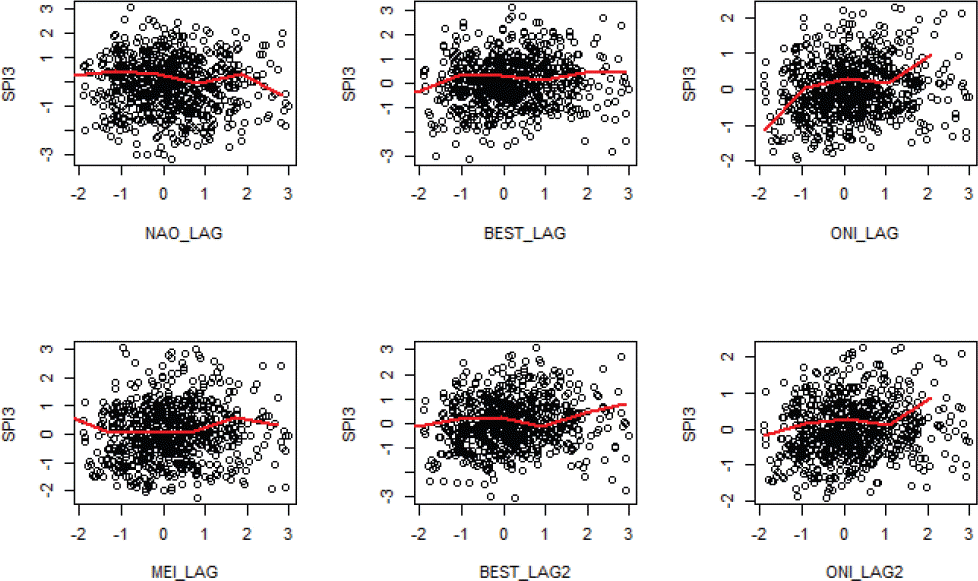
분석하기에 앞서 서울 표준강수지수와 설명변수들 사이의 산점도들 중 일부를 통해 선형상관성이 매우 낮아서 선형회귀모형으로 적합하기에 매우 어려움을 알 수 있다(Fig. 1). 이러한 한계를 극복하는 방법의 일환으로 전술한 바와 같이 평활스플라인 함수와 가법모형을 적용하여 가뭄예측모형을 구성하였다.
Sample Scatter Plots for Dependent Variable (SPI3) and Independent Variables
2.2 가법 모형(Additive Model)
우리가 여러 분석에서 사용하고 있는 모형은 선형회귀모형의 적용성이 높으나 사회과학분야와 같이 선형 상관성으로 문제를 해결하기 힘든 경우에 있어 가법모형의 적용성이 높아지고 있으며 Back(2011)는 일반화 가법모형에 대한 비교⋅고찰 결과를 제시하였다. Fig. 1과 같이 종속변수와 설명변수들 간의 선형성이 거의 대부분 없는 가뭄현상의 경우 가법모형의 적용성이 높을 것으로 판단된다. 가법모형 데이터를 선형에 강제로 맞추려 하기 보다는 평활스플라인 함수로 보다 유연하게 풀어주는 모형이다. 가법모형은 p개의 설명변수 X1,X2,…,Xp에 대해f1, f2,…, fp인 평활스플라인 함수로 세운 다음 전부 합한 모형으로 다음과 같다.
여기서, ε은 평균이 0, 분산이σ2인 오차항이다. 또한
2.2.1 평활스플라인(Smoothing Spline) 함수
적절한 평활스플라인 함수는 Eq. (2)에서 나타내는 바와 같이 잔차제곱합이 작으면서 비교적 매끄러운 곡선을 말한다. 즉, Eq. (2)를 최소로 하는 f이다.
여기서, Eq. (2)의 오른쪽 앞항은 잔차제곱합 즉, 모형적합도이고, 뒷항은 함수의 매끄러운 정도를 나타낸다. 그리고λ는 모형적합도와 매끄러운 정도의 균형을 나타내는 값으로 이를 평활모수(smoothing parameter)라고 부른다. λ의 값이 매우 작을 경우, Eq. (2)를 최소로 하는 것은 잔차제곱합을 최소로 하는 경우와 유사한 결과를 가진다. 반대로 λ의 값이 매우 클 경우는 두 번 미분한 함수의 제곱을 구한 [a, b]에서 적분한 값을 최소로 해야 하므로 f는 직선 식에 가깝게 된다. 이렇게 되면 함수형태가 유연하지 않게 되어 해석에 어려울 수 있다. 따라서 적절한 λ값을 적용하여 최적 평활스플라인함수를 찾아야 한다(Wood, 2003). Eq. (2)를 최소화시키는 평활스플라인함수의 조건은 각 값들이 매듭(knot)을 가져야 되고, 각 매듭에 대해 1차 도함수와 2차 도함수가 연속이어야 하며, 매듭의 외부영역이 선형으로 나타내어야 한다. 이에 만족하는 함수가 바로 자연평활스플라인(natural smoothing spline)함수이다. 이 함수의 식은 다음과 같다.
여기서 Nj(x)는 자연평활스플라인에 대한 기저함수(basis function)를 나타내고, βj는 자연평활스플라인계수이다. 그래서 평활스플라인함수를 추정하기 위해서 Eq. (4)를 최소화하는 평활스플라인계수β를 찾아야한다.
여기서 y=(y1,y2….,yn)’ {N}ij=Nj(xi), β=(β 1,β 2….,βn)’,
Math (5)
그래서 위의 추정치를 통해 평활스플라인함수 추정치는 다음과 같다.
그리고, 평활스플라인함수 추정치를 벡터로 표시하면 다음과 같다.
여기서 Sλ=(I+λK)−1은 평활행렬(smoother matrix)이고, K=(NT)−1ΩNT는 패널티행렬(penalty matrix)이다.
평활모수λ는 유효자유도(effective degrees of freedom)를 조절하는 역할을 한다. 여기서, 유효자유도는 평활스플라인 함수의 유연성을 나타내는 측도이다. 즉, 유효자유도 값이 클수록 평활스플라인 함수가 보다 매끄러운 곡선이 된다. 유효자유도의 식은 평활행렬(smoother matrix)의 대각원소들의 합으로 나타난다.
평활모수 λj의 추정법으로 가장 널리 사용되는 것이 CV(Cross Validation) 또는 GCV(Generalized Cross Validation)이며, 이 때 CV와 GCV를 최소로 하는 λj의 추정값을 구한다.
여기서 n개의 관측치 중에서 i번째 관측치를 제외한 후 (n−1)개의 관측치로 추정된 f의 추정치를
으로 정의된다. 이 때 GCV는 CV보다 계산이 보다 편리하므로 널리 사용된다.
2.2.2 Penalized Iteratively Reweighted Least Squares(P-IRLS)
종속변수가 지수족(exponential family) 분포를 따르는 경우에 나타나는 가법모형을 일반화가법모형(Generalized Additive Model)이며 식은 다음과 같다.
일반적으로 일반화 가법모형은 연결함수(link function) g를 어떻게 정의하느냐에 따라 다양한 형태의 모형이 될 수 있다.
여기서 본 연구에서 사용된 가뭄지수인 표준강우지수가 가우시안 분포를 따른다고 가정할 수 있으므로, 이 때 쓰이는 연결함수는 항등연결 g(μ)= μ이고 추정할 가법모형의 형태는 다음과 같이 나타난다.
위의 모형을 추정할 알고리즘으로 Penalized Iteratively Reweighted Least Squares(P-IRLS) 방법을 사용하였으며 식은 다음과 같다.
여기서 k는 반복횟수이고, Z[k]=Xβ[k]+(y−μ[k]) 로 나타내고, y=(y1,y2,…,yn),
위의 추정치를 통해 평활행렬과 유효자유도를 구할 수 있고, 추정치와 평활행렬을 통해 적절한 평활모수λj를 구한다.
2.2.3 Double Penalty Approach(DPA)
가법모형의 단점 중 하나가 바로 과대적합 문제를 해결하기 위하여 유의하지 않은 변수들을 제거하여야 한다. 그래서 여러 가지의 변수선택방법들 중 본 연구에서 사용된 방법은 Double Penalty Approach(DPA)이다(Marra and Wood, 2011). 먼저, 행렬 Ωj을 분해하면 다음과 같다.
여기서, Λj는 대각원소가 Ωj의 고유값(eigen value)인 대각행렬이고, Uj는Ωj의 고유값에 대한 고유벡터(eigen vector)들로 구성된 행렬이다. 평활기저집합(smoothing basis space)의 일부가 벌점 영공간(penalty null space)을 가진다는 사실은Λj에서 고유값이 0인 것을 포함한다고 말한다. 이것은 변수선택을 할 때 문제가 된다. 벌점행렬(penalty matrix) Ωj는 다음과 같은 식을 나타낸다.
여기서, ei는Ωj의 고유값이고, ui는ei에 대한 고유벡터이다. 이 때, 고유값이 0인 부분에서ei=0이기 때문에, 이에 대한 고유벡터의 곱으로 구성된 행렬(
그 결과, 평활모수 값이λi*을 추가로 더해지면서 점점 커지게 되고, 그렇게 되면, 평활스플라인 함수 추정치
3. 적용
모형의 적합성을 평가하기 위하여 1954년~2013년까지의 자료를 모형 적합자료로 산정된 7개의 지점(서울, 인천, 대구, 추풍령, 제주, 목포, 강릉)별 가법모형과 선형회귀모형을 구축한 후에 검증기간 2014년~2015년에 대하여 각 모형에 대한 MSE값을 산정하여 가뭄예측의 정확도를 분석하였다. 가법모형과 선형회귀모형을 비교하기 위해 모의실험을 다음과 같이 실시하였다. 반응변수는 현재 시점에 대한 7개 지역(서울, 인천, 대구, 추풍령, 제주, 목포, 강릉)의 표준강수지수(SPI-3)로 두고 설명변수 구성을 달리하여 세 경우에 대하여 적용하였다. 모의실험 case 1의 경우 한 달 전의 각 지역별로 표준강수지수, 기온, 강수량, 강수일수, 그리고 세계기후지수(Lag1)을 설명변수로 설정하였다. 모의실험 case 2의 경우 두 달 전의 각 지역별로 표준강수지수, 기온, 강수량, 강수일수, 그리고 세계기후지수(Lag2)을 설명변수로 설정하였다. 모의실험 case 3의 경우 한 달 전과 두 달 전의 각 지역별로 표준강수지수, 기온, 강수량, 강수일수, 그리고 세계기후지수(Lag1+2)을 설명변수로 설정하였다.
Table 3에서 제시한 선형모형과 가법모형의 결과를 보면, 제주도와 강릉지역을 제외한 나머지 5개 지역(서울, 인천, 대구, 추풍령, 목포)에서 가법모형의 Test MSE값이 가장 낮게 나왔다. 즉, 5개 지역에서는 가법모형으로 한 달 전의 설명변수들로 현재시점의 가뭄지수를 예측하는 것이 더 좋은 결과를 보였다. Table 4의 결과는 추풍령, 강릉지역을 제외한 나머지 5개 지역(서울, 인천, 대구, 제주, 목포)에서 가법모형의 Test MSE값이 가장 낮게 나타났다. 즉, 5개 지역에서는 가법모형으로 두 달 전의 설명변수들로 현재시점의 가뭄지수 예측하는 것이 더 좋은 결과를 보였다. 그러나 Table 3의 결과와 비교를 하면, 두 달 전보다 한 달 전의 설명변수들로 현재시점의 가뭄지수 예측이 더 좋은 결과를 보였다. 마지막으로 Table 5의 결과를 보면, 전체 7개 지역(서울, 인천, 대구, 추풍령, 목포, 강릉)에서 가법모형의 Test MSE값이 가장 낮게 나왔다. 즉, 7개 지역에서는 가법모형으로 한 달 전과 두 달 전의 설명변수들로 현재시점의 가뭄지수 예측이 가장 좋은 결과를 보였으며 Tables 3과 4를 비교하면 전체적으로 7개 지역 모두 가법모형으로 한 달 전과 두 달 전의 설명변수들로 현재시점의 가뭄지수 예측하는 것이 가장 좋은 결과를 보였다.
Test MSE Comparison between a Linear Regression Model and the Additive Model for Case 1
Test MSE Comparison between a Linear Regression Model and the Additive Model for Case 2
Test MSE Comparison between a Linear Regression Model and the Additive Model for Case 3
그러나 모의실험 case 3에서의 설명변수들의 개수가 너무 많아서 가법모형으로 구축하였을 때 과대적합문제가 발생하여 가뭄 예측의 정확성이 떨어질 가능성이 있다. 그래서 각 지역별 모의실험 case 3에서의 가법모형에 대하여, DPA 방법으로 변수선택을 하여서 가뭄 예측 결과를 비교하였다.
Table 6의 결과를 보면 모든 지역에서 DPA 방법으로 변수선택 후의 Test MSE 값이 더 낮아 가장 좋은 성능을 보이는 것으로 나타났다. Skill Score(SS)와 Nash-Sutcliff Efficiency(NSE)의 경우도 0보다 큰 값을 가지므로 Persistence 보다 좋은 성능을 보인다고 할 수 있다. 또한, 변수선택 전과 비교하였을 때 SS와 NSE가 상대적으로 크므로 변수선택 전 보다 변수선택 후 성능이 더 좋아졌다. 이는 유의하지 않은 설명변수들이 가뭄 예측성을 향상에 기여하지 못하므로 이러한 변수들을 소거한 후에 적절한 변수의 조합으로 구성된 모형결과가 전체 자료를 사용할 때 보다 개선된 가뭄 예측 결과를 보이는 것으로 판단된다. Table 7은 각 지역별로 선택된 유의한 변수들을 나타낸다. Fig. 2(a)는 서울지점에 대한 모의실험 case1의 결과로 파란색 점선인 가법모형의 결과가 다른 모형 결과에 비해 예측성이 높음을 보이며 Figs. 2(b)와 (c)는 모의실험 case2와 case3의 결과로 이 또한 가법모형의 결과가 다른 모형 결과에 비해 예측성이 높음을 보였다. Fig. 2(d)는 변수선택 전과 후의 가법모형 적용에 따른 가뭄 예측 결과를 보여주며 변수선택 후의 결과가 개선됨을 보였다.
Test MSE Comparison between Before and After Variable Selection Process
Significant Variables for Each Sample Sites
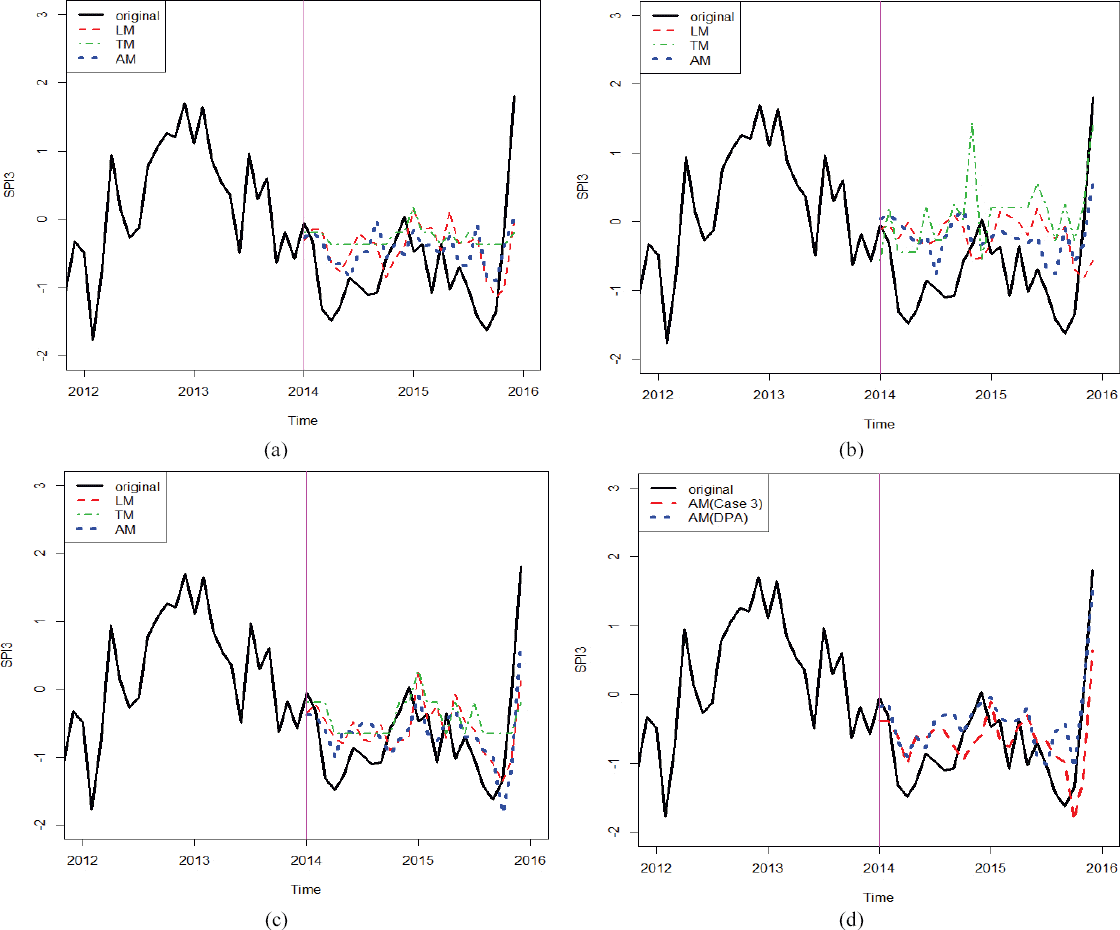
Sample Plots of Comparison between Observation and Model Results for the Seoul Site (a) Case1, (b) Case 2, (c) Case 3, (d) Appling Variable Selection Process (original: original value, LM: Linear Model, AM: Additive Model, TM: Tree Model, AM(Case3): Additive Model about Case3, AM(DPA): Additive Model using DPA method after Variable Selection)
4. 결론
본 논문에서는 가뭄현상의 시간적 비선형 변동 특성을 보다 잘 설명하는 평활스플라인 함수와 가법모형을 적용하여 가뭄예측모형을 구성하였다. 또한, 가법모형의 적용 시 발생할 수 있는 과대적합문제를 해결하기 위해 변수선택법인 DPA 방법을 적용하여 가뭄 지수 예측을 개선하였다. 모형 구성은 종속변수가 현재 시점에 대한 7개 지역(서울, 인천, 대구, 추풍령, 목포, 강릉)의 표준강수지수(SPI-3)이고, 설명변수는 과거 시점(한 달 전, 두 달 전)에 대한 7개 지역의 표준강수지수, 기온, 강수, 강수일수 그리고 세계기후지수를 적용하였다. 1954~2013년 동안에 모형적합을 수행하였으며 2014~2015년에 대하여 각각의 모형에 대한 적합성을 선형회귀모형과 비교⋅검증하였다.
한 달 전 자료를 사용한 case 1의 경우에서는 제주도와 강릉지역을 제외한 5개 지역만 가법모형 적용으로 MSE가 감소하여 가뭄 예측이 개선되었으며, 두 달 전 자료를 사용한 case 2의 경우에서는 강릉지역을 제외한 6개 지역에서 가법모형 적용으로 MSE가 감소하여 가뭄 예측이 개선되었다. case 3에서는 전체 7개 지역이 가법모형 적용으로 MSE가 감소하여 가뭄 예측이 개선되었다. 그러나 case 3의 경우 설명변수들이 많아 가법모형의 문제점인 과대적합문제가 발생하였다. 이러한 문제를 해결하기 위하여 변수선택방법으로 DPA 방법을 적용하여 유의하지 않은 변수들을 제거한 후 가법모형을 적용하여 가뭄 예측을 하였고 이 경우 가뭄 예측에 있어 개선된 결과를 보였다. 변수선택의 경우 각 지역별로 유의한 세계기후지수는 서로 다르지만, 각 지역별 한 달 전과 두 달 전의 강수량과 한 달 전의 기온 그리고 한 달 전의 표준강수지수는 공통적으로 가뭄에 큰 영향을 미치는 것으로 나타났다. 본 연구에서 적용한 평활스플라인 함수와 가법모형의 적용과 DPA방법을 적용을 통한 유의변수들의 선택적용을 통하여 가뭄예측이 개선될 것으로 판단된다.
감사의 글
본 연구는 국립기상과학원 연구개발사업 “기상업무지원기술개발연구”의 일환으로 수행되었습니다.