Article information

J. Korean Soc. Hazard Mitig. 2018;18(2):271-280

Publication date (electronic) : 2018 April 21

doi : https://doi.org/10.9798/KOSHAM.2018.18.2.271

Ho Min Lee^*, Hwandon Jun^**, Seung Cheol Baek^***, Joong Hoon Kim^,****

^*Member, Research Professor, Research Center for Disaster Prevention Science and Technology, Korea University

^**Member, Professor, Department of Civil Engineering, Seoul National University of Science and Technology

^***Deputy General Manager, UnU Inc.

^****Member, Professor, School of Civil, Environmental and Architectural Engineering, Korea University

이호민^*, 전환돈^**, 백승철^***, 김중훈^,****

^*정회원, 고려대학교 방재과학기술연구소 연구교수

^**정회원, 서울과학기술대학교 건설시스템공학과 교수

^***(주)유앤유 차장

^****정회원, 고려대학교 건축사회환경공학부 교수

교신저자: 김중훈 Tel: +82-2-3290-3316, Fax: +82-2-3290-4722, E-mail: jaykim@korea.ac.kr

Received 2017 November 21; Revised 2017 November 23; Accepted 2017 December 6.

Abstract

Trans Abstract

1. 서 론

상수도 관망 시스템의 역할은 각 수요가에서 필요로 하는 충분한 양의 물을 적절한 수압과 수질을 확보하며 공급하는 것이다. 근래의 상수도 관망 시스템의 운영은 단수를 최소화하는 안정적 공급체계 구축과 안전한 물 공급을 동시에 추구하고 있으나, 상수도 관망 시설에 발생하는 다양한 비정상상황으로부터의 위협이 증가하므로 탄력적 상수도 관망 시스템의 구축과 안정적 관리의 필요성이 강조되고 있다. 기존 상수도 관망의 설계, 관리 기술은 비용적인 측면에서의 효율성 확보에 집중하였으나, 최근 도시화에 따른 수요가의 요구수준이 증가, 기후변화, 홍수와 가뭄, 지진 등 다양한 비정상상황의 발생 등은 적극적 상수도 관망 관리에 대한 필요성을 증대시키고 있으며, 이를 위해 기존의 단편적 대응에서 벗어난 새로운 방식의 계획 및 관리 기술의 도입이 필요하다.

이와 같은 안전하고 안정적인 물의 공급을 위해 상수도 관망의 계획 및 설계, 시공, 유지관리와 운영 측면에서 상수도 관망의 수리해석 모형은 다양한 시나리오에 대한 관망의 수리학적, 수질적 인자의 거동을 예측하는 데에 효과적인 도구로 활용된다. 상수도 관망에 발생 가능한 다양한 비정상상황에 대한 보다 정밀하고 정확한 모의를 위해 Pressure Driven Analysis (PDA) 기법이 기존의 Demand Driven Analysis (DDA) 기법을 대체해가고 있으나, 이러한 DDA 및 PDA 기반 수리해석 모형들은 수원의 공급량이 무한하다는 가정을 포함하며, 이에 따라 수요량 급증, 비상 수계전환 실시 등 수원의 저류량에 큰 영향을 미칠 수 있는 비정상상황에 대한 해석 과정에서 시스템의 거동을 정확하게 모의할 수 없다는 공통된 문제점을 지닌다.

따라서 이와 같은 기존 수리해석 모형의 단점을 개선하기 위해 수원의 저류량의 규모를 고려할 수 있는 고도화된 상수도 관망 수리해석 모형이 필요하며, 본 연구에서는 기존 수리해석 모형의 무한수원 가정을 개선한 Advanced-Pressure Driven Analysis (A-PDA) 기법을 제안하였다. A-PDA 모형에서는 수원의 저류량을 고려하기 위해 수원의 수위와 저류량 관계, 시간에 따른 수원으로의 유량 등을 추가 요소로 활용하였다. 또한 제안한 모형을 검증하기 위해 가상의 상수도 관망 시스템의 해석에 적용하였으며 기존 DDA 및 PDA 수리해석 모형과의 비교를 통해 적합성을 평가하였다.

2. 상수도 관망 수리해석 기법

상수도 관망의 수리학적 해석 방법에는 크게 두 가지가 있으며, 하나는 주로 정상상황의 시스템 해석에 사용되는 DDA이고, 다른 하나는 비정상상황 시스템 해석에 사용되는 PDA이다(Lee et al., 2013, 2016). 기존에 대부분의 상수도 관망의 수리해석 과정에서 적용되어 온 DDA는 각 수요지점의 수요량을 수압에 상관없이 항상 100% 공급된다는 것을 기본 가정으로 한다. DDA 기법은 상수도 관망 시스템이 정상상태일 경우에는 해석에 무리가 없으나, 특정 원인으로 인하여 관망의 수리학적 상태가 변화하여 절점의 수압이 감소하는 경우(관 파손, 수요량 급증, 가압장 운영중단 등), 절점에서의 부압이 도출되는 등 비현실적인 결과를 발생시킬 수 있다. 이와 같은 단점을 보완하기 위하여 새롭게 제안된 기법이 PDA이며, PDA에서는 절점의 수두와 공급량을 모두 미지수로 하여 절점의 수두와 공급가능 유량의 관계식(Head-Outflow Relation, HOR)을 통해 비정상상황에서의 수두 및 공급량을 산정한다.

본 연구에서는 국내외에서 가장 범용적으로 활용되고 있는 EPANET2.0 (Rossman, 2000) 수리해석 프로그램과, 해당 프로그램을 수정, 보완하여 Lee et al.(2013, 2016)에 의해 개발된 Segment-based PDA (SB-PDA)의 수치해석기법인 Gradient Algorithm과 Global Gradient Algorithm의 세부 구조를 파악하였으며, 이를 확장하여 유한수원을 고려한 수리해석 모형인 A-PDA 모형을 개발하였다. 또한 개발된 A-PDA 모형의 검증을 위해 가상의 상수도 관망 시스템의 비정상상황에 대한 수리해석을 수행하였다.

3. Advanced-Pressure Driven Analysis(A-PDA) 모형의 개발

3.1 유한수원의 정의 및 연산과정

본 연구에서는 유한수원을 고려한 수리해석 모형을 개발하기 위해, EPANET2.0의 수리해석 알고리즘을 확장하여 개발된 Lee et al.(2013, 2016)의 Global Gradient Algorithm 기반 PDA 모형인 SB-PDA의 엔진의 세부 구조와 연산 과정을 파악하는 작업을 진행하였다. 그 결과 각각의 행렬 요소 및 시스템 구성 인자의 관계를 파악할 수 있었으며 알고리즘 개량을 위한 방법론을 설정할 수 있었다. 개발된 A-PDA에서는 유한수원을 구현하기 위해 먼저 수원에 수위에 따른 저류용량 관계식, 최대 저류 가능 용량 및 수위 경계조건, 수원의 고도를 입력자료로 구성하였으며, 시간에 따라 수원으로 유입되는 유량을 정의하기 위해 평균 유입량과 유입패턴을 수원의 특성으로 추가하여 새로운 형태의 수원 객체를 생성하였다.

따라서 각 시간대별로 유한수원으로 유입되는 유량과, 해당시간대에 절점으로 유출되는 유량을 산정하여 각 유한 수원의 저류량을 갱신하는 과정을 반복적으로 수행하며, 만약 특정 시간 구간에 저류량이 ‘0’인 경우, 저류량이 ‘0’이 되는 시간을 초단위로 환산하여 해당 시간을 메시지로 출력한다.

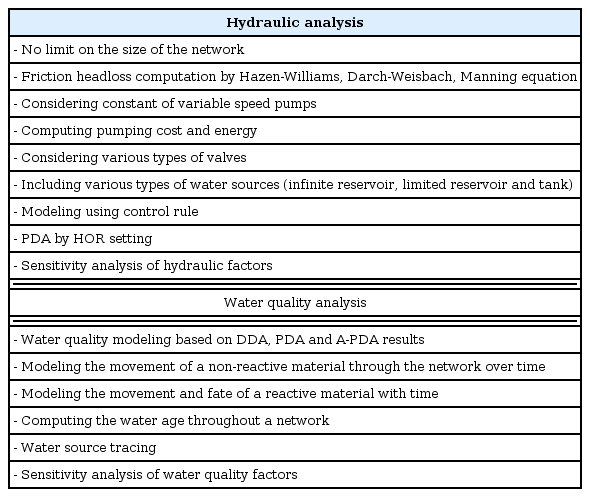
이를 통해, 본 연구에서 개발된 A-PDA는 수리 및 수질해석이 가능하며, 주어진 상수도 관망 시스템에 대해 손실수두 산정 기법, 펌프 곡선 및 효율, 밸브 구성, 유한/무한 수원 및 탱크 구성, 제어규칙, HOR 관계식 매개변수 설정 등에 따라 해석을 수행하며, 본 모형을 통해 해석 가능한 수리 및 수질해석의 범위는 Table 1과 같다.

Table 1.

Modeling Capabilities of A-PDA

3.2 A-PDA 개발 환경

A-PDA 모듈은 방대한 수치해석과정을 포함하므로 효율적이며 빠른 연산이 가능한 컴파일러를 사용하는 것이 좋다. 따라서 본 연구에서는 수치해석 연산 시간을 단축하기 위하여 Table 2와 같은 개발환경에서 모듈을 개발하였다.

Table 2.

Development Tool and Version

개발 운영체제는 Windows 10이며 이외에 Windows Vista 이상의 버전에서 사용이 가능하도록 개발하였다. 컴파일러의 경우, 수치해석에 절리 적용되는 Native C를 적용하여 연산시간을 최소화하도록 구현하였다. 개발 도구는 Microsoft Visual Studio 2015 버전을 사용하였으며, 개발 하드웨어는 Intel I5 계열 PC를 사용하였다. A-PDA의 개발을 위하여 별도의 3^rd Party 컴포넌트는 사용하지 않았으며, 개발된 A-PDA 모듈은 Dynamic Linking Library (DLL) 형태로서 독립실행이 되지 않는 Windows 응용프로그램이므로 실행파일로 빌드되는 프로그램의 구성요소로써 사용되도록 구성하였다.

3.3 수리해석 모형 간 비교

Table 3과 같이, PDA 모형에서는 기존 DDA 모형에서 고려하지 않는 절점의 수압에 따른 공급가능 유량을 모의하기 위해 각 수요절점에 최소 및 충족수두(Hjmin, Hjreq)와 오리피스 방정식 지수 (n)을 통해 정의되는 HOR을 추가로 고려한다. 이에 따라 각 절점에서의 공급가능 유량은 수압조건에 의해 산정되며 수압저하 비정상상황에서 DDA 모형의 부압 발생 등의 문제를 해결할 수 있었다. 나아가 본 연구를 통해 제안된 A-PDA 모형의 경우, PDA 모형을 확장하여 수원의 저류량을 고려하기 위하여 수원에 수위에 따른 저류 용량 관계식, 최대 저류 가능 용량 및 수위 경계조건, 수원의 고도, 시간에 따라 수원으로 유입되는 평균 유입량 및 유입패턴을 추가하였다.

Table 3.

Characteristic Comparisons among Hydraulic Analysis Models

이에 따라 A-PDA의 경우, 절점의 수압이 저하되는 비정상상황과 함께 수원의 저류량이 부족한 비정상상황에 대한 해석 적합도가 기존 모형들에 비해 높다는 장점이 있다.

3.4 A-PDA 구동 화면 예제

A-PDA에서는 기존의 DDA 및 PDA 모형의 입력파일을 불러들일 수 있으며, 또한 A-PDA를 위한 추가조건들이 포함된 입력파일을 입력, 출력 할 수 있다. Fig. 1은 Ozger(2003)의 연구에서 사용된 관망을 A-PDA 상에서 불러들인 예제이다.

Fig. 1.

Sample Network Visualization

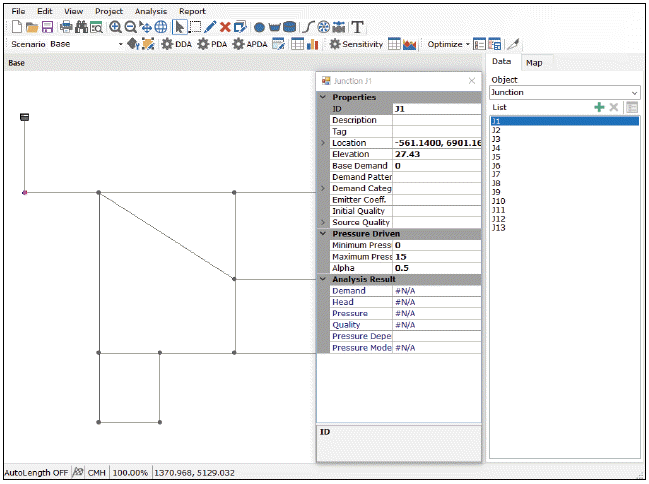
또한 A-PDA에서는 기존 수리해석 모형들과 마찬가지로 각 수원, 절점, 관로 별 속성정보를 정의할 수 있다. Fig. 2의 경우, 해당 관망의 절점 J1의 정보를 입력한 예를 나타내며, 절점의 수압에 따른 공급가능 유량을 산정하기 위한 HOR 관계식의 매개변수를 정의할 수 있다.

Fig. 2.

Nodal Property Setting

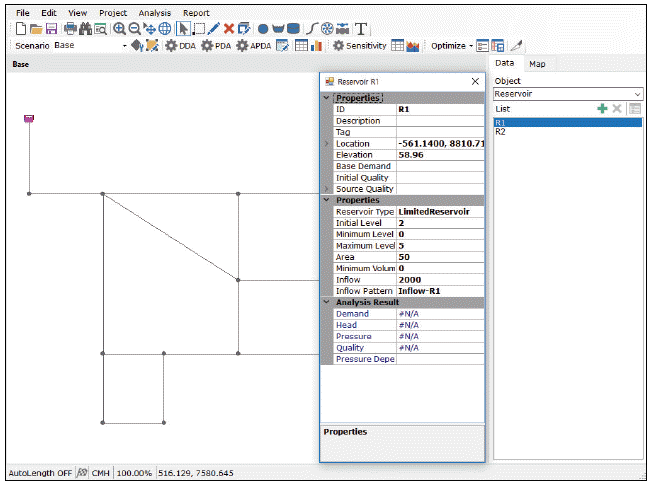
또한 A-PDA에서는 수원의 종류를 총 세 가지로 설정가능하며, 이는 유한/무한 수원 및 탱크를 포함한다. A-PDA에서는 Fig. 3과 같이 새롭게 추가된 유한수원을 정의하기 위한 저류용량 관계식, 최대 저류 가능 용량 및 수위 경계조건, 수원의 고도, 평균 유입량과 유입 패턴을 설정할 수 있다.

Fig. 3.

Source Property Setting

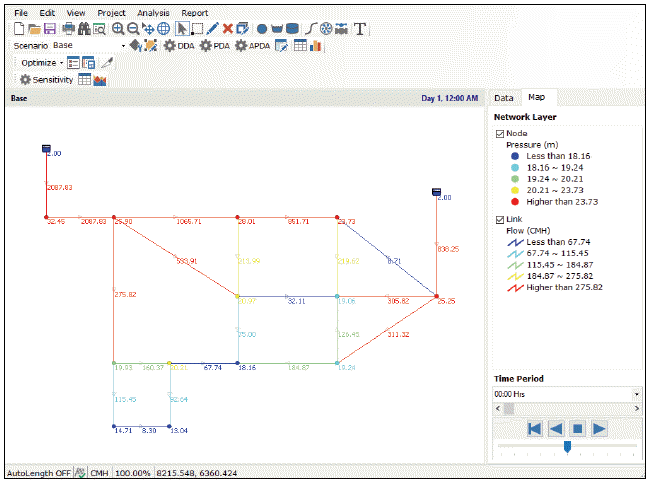
한편, 해당 관망에 대해 해석을 수행하면 각 시간에 따른 수리 및 수질해석 결과를 획득할 수 있으며, Fig. 4의 경우 초기 계산 시간에 대한 절점의 수압과 관로의 유량을 도시화한 예시를 나타낸다. 해석 결과의 경우, 다양한 형태의 표와 그래프로도 출력 가능하며 표출 가능한 속성은 Table 4와 같다.

Fig. 4.

Display of Hydraulic Analysis

Table 4.

Result Display Items in the A-PDA

4. 모형의 적용

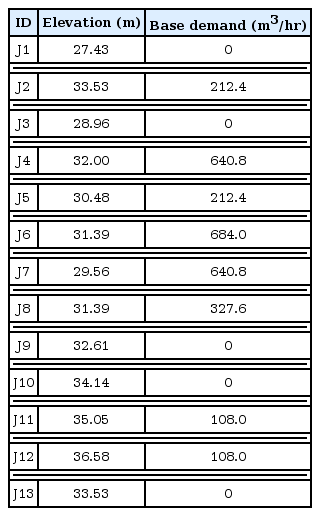
본 연구에서는 제안한 A-PDA 모형의 적합도를 검증하기 위해 Ozger(2003)의 연구에서 사용된 가상관망을 그 대상으로 선정하였다(Fig. 5). 해당 관망의 경우, 총 두 개의 수원(R1, R2)으로 이루어져 있으며, 13개의 절점 (J1~J13)과 21개의 관로(Pipe1~Pipe21)로 구성되어 있고, 관망의 수원, 절점, 관로에 대한 정보는 각각 Tables 5~7과 같다. 기존 문헌에서는 해당 관망에 대해 고정기간 모의 (Steady State Simulation)를 수행하였으나, 본 연구에서는 유한수원의 적용을 위해 이를 1시간 단위로 총 1주일 기간의 확장기간 모의 (Extended Period Simulation)로 변환하였다.

Fig. 5.

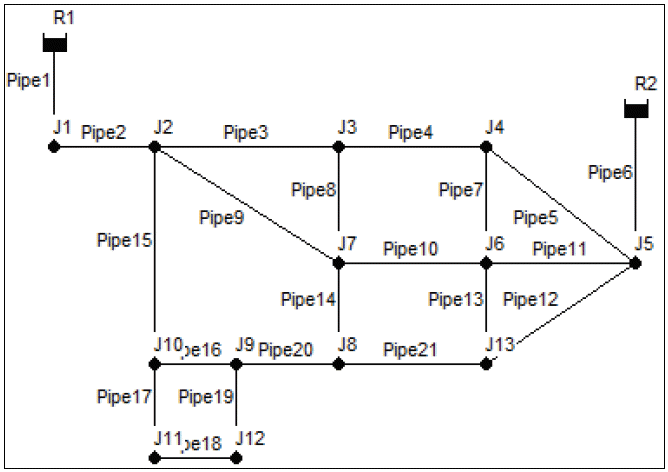
Layout of Hypothetical Network (Ozger, 2003)

Table 5.

Water Source Properties

Table 6.

Node Properties

Table 7.

Link Properties

PDA 및 A-PDA의 적용을 위해서는 각 절점에 HOR을 설정하는 것이 필요하며, 이에 따라 각 절점의 최소 및 충족수두를 각각 절점의 고도와 고도보다 15 m 높은 수두조건을 가정하였으며, 또한 오리피스 형태 HOR의 지수는 0.5를 적용하였다.

다음으로, A-PDA에서는 기존 관망의 무한수원 (R1, R2)를 유한수원으로 변환하는 과정이 필요하며, 이에 따라 각 유한수원의 고도를 기존 무한수원의 수두보다 2 m 낮은 58.96 m로, 초기 수위를 2 m로 가정하여 기존 무한수원의 초기 수두를 유지할 수 있도록 하였다. 다음으로 각 유한수원의 최소 및 최대 수위는 각각 0 m, 5 m로 설정하였으며 수위에 관계없이 1,000 m²의 동일한 단면적을 갖는 저류지인 것으로 가정하였다.

마지막으로 유한수원으로의 시간에 따른 유입량을 가정하기 위해 대상 가상 관망의 정상상황에 대해 DDA 수리해석을 수행하였다. 수행결과 R1과 R2로부터 상수도 관망에 각각 2,094.66 m³/hr, 839.34 m³/hr의 유량을 공급하는 것으로 나타났으며, 이에 따라 해당 유량 값을 R1과 R2로 유입되는 평균 유입량으로 가정하였다. 한편 각 유한수원으로 유입되는 유량의 패턴의 경우, 간략화된 모의를 위해 시간에 따라 변화하지 않고 일정한 값이 유입되는 것으로 가정하였다.

해당 관망의 정상상황에 대한 DDA, PDA 및 A-PDA를 적용한 수리해석 결과는 Table 8과 같다. DDA의 경우, 절점의 수압 조건에 관계없이 수요량을 100% 공급시킨다는 가정을 전제로 하므로 각 절점의 수요량(Table 6)을 모두 공급 가능하다는 결과가 도출된 반면, PDA 및 A-PDA에서는 절점의 수압 조건에 따라 공급가능 유량을 산정하므로 절점의 수두가 충족수두 이하인 절점(J11, J12)에 대해서는 유량을 일부분만 공급 가능한 것을 확인할 수 있었다.

Table 8.

Result Comparisons among Hydraulic Analysis Models (normal condition)

또한, 기존의 DDA와 PDA의 경우, 두 수원(R1, R2)이 모두 무한수원으로 가정되었기 때문에 시간 변화에 관계없이 일정한 수두값을 가지므로 모든 시간 구간에서 동일한 해석 결과를 보이는 반면, A-PDA의 경우 각 시간대 별 유한수원의 저류량 변화에 따라 수위가 변화하며, 해당 수위가 각 절점의 수압에 영향을 주므로 절점의 공급가능 유량이 변화하는 것을 확인할 수 있다. 따라서 본 연구를 통해 제안된 A-PDA의 경우, 절점의 수압에 따른 공급가능 유량을 고려함과 동시에, 수원의 저류량 변화를 고려하므로 상수도 관망 시스템의 수리해석 과정에서 각 지점별 공급성을 시간 및 공간적으로 보다 실제 시스템의 거동에 근사하게 도출할 수 있는 장점이 있는 것을 확인할 수 있다.

다음으로, 상수도 관망의 비정상상황에 대한 개발 모형의 적용성 검토를 위해 Ozger(2003) 관망의 Pipe1에 사고가 발생하여 두 지점의 수원 중 R1로부터 유량공급이 불가능한 상황을 가정하였다. 해당 시나리오에서 DDA, PDA 및 A-PDA를 각각 적용한 수리해석 결과는 Table 9와 같다. DDA 모형을 통한 해석 결과에서는, 각 수요절점의 수요량을 100% 만족시키기 위해 각 관로에 과도한 유량이 흐르는 것으로 모의가 되며, 이에 따라 손실수두가 과대추정 되므로 절점에 부압이 발생하는 비현실적 결과가 도출되는 것을 확인할 수 있다. 반면, PDA의 적용 결과 절점의 수압에 따른 공급가능 유량을 산정하므로 DDA에서 나타나는 부압 등 비현실적인 해석 결과를 보완할 수 있는 것으로 나타났다. Pipe1이 차폐된 비정상상황에 대해 전체 관망 시스템에서 요구되는 수요량 2,934.00 m³/hr 중 54.88%인 1,610.28 m³/hr가 공급 가능한 것을 확인할 수 있었다.

Table 9.

Result Comparisons among Hydraulic Analysis Models (Pipe1 failure condition)

한편, DDA와 PDA의 적용 결과에서는 비정상상황시 대상 관망으로 유량을 공급하는 수원인 R2가 무한수원이라는 가정을 포함하므로, 앞선 적용사례와 마찬가지로, 해당 수원이 시간 변화에 관계없이 일정한 수두값을 가지므로 모든 시간 구간에서 동일한 해석 결과를 나타낸다. 반면, A-PDA에서는 Pipe1이 차폐된 최초시간 (00:00 hrs)에서는 PDA와 동일한 수리해석 결과를 나타내나, 시간에 따라 유한수원 R2의 저류량이 감소하게 되며, 수위의 저하에 따라 절점의 수압이 감소하고 절점별 공급가능 유량 또한 감소하는 것을 확인할 수 있었다. 또한 비정상상황이 발생 2시간 37분 이후에는 R2의 수위가 0.04 m까지 감소하여 해당 시간에 전체 시스템에 공급가능한 유량은 약 52.82%인 1,549.85 m³/hr로 산정되었으며 이후의 시간에 대해서는 시스템에 유량이 정상적으로 공급되지 못하는 결과를 나타냈다.

이처럼, A-PDA 모형은 절점의 수압에 따른 공급가능 유량 산정과 동시에 수원의 저류량을 고려함에 따라 상수도 관망 시스템 전반에 걸친 공급성을 시간 및 공간적으로 도출할 수 있다는 것을 확인할 수 있었으며, 특히 상수도 관망이 비정상상황에 있는 경우, 기존 수리해석 모형들에 비해 보다 현실적인 수리해석 결과를 산정할 수 있다는 것을 확인할 수 있었다. 이를 통해 기존 DDA 및 PDA 모형에서는 도출할 수 없었던 비정상상황 발생시 상수도 관망 시스템에 지속적으로 유량 공급을 할 수 있는 기간을 도출할 수 있었으며, 이는 실무적인 관점에서 해당 상황에 대한 적절한 대응을 할 수 있도록 의사결정을 지원하는 데에 효과적으로 적용될 수 있을 것으로 기대된다.

5. 결 론

상수도 관망 시스템의 해석에 적용되어온 DDA와 PDA 모형은 수리해석 과정에서 수원의 저류량은 무한하다는 무한수원의 가정을 통해 고정된 수원의 수두를 기준으로 하여 각 절점의 수압, 관로의 유량 등을 산정한다. 하지만 이러한 수리해석 모형은 대상 상수도 관망 시스템이 수원으로부터 충분한 유량을 지속적으로 공급받을 수 있는 상황에대해서는 비교적 타당한 결과를 도출하지만, 특정 수원으로부터의 유량공급이 불가능한 경우 등 수원의 저류량에 직접적인 영향을 미치는 상황에 대해서는 현실적인 결과를 도출하지 못하는 단점이 있다.

따라서 본 연구에서는 기존 DDA 및 PDA 모형에서 무한수원 가정으로 인해 발생하는 문제점을 파악하고, 이를 보완하기 위한 대안으로 유한수원을 고려한 A-PDA 모형을 개발하였다. 이를 위해 기존 수리해석 모형의 수치해석 기법인 Gradient Algorithm 및 Global Gradient Algorithm의 구조를 분석하였으며, 이를 바탕으로 수원에 수위에 따른 저류용량 관계식, 최대 저류 가능 용량 및 수위 경계조건, 수원의 고도, 수원으로 유입되는 평균 유입량과 유입 패턴을 수원의 특성으로 추가하여 새로운 형태의 유한수원 객체를 생성하였다.

또한 개발된 모형을 통한 수리해석 결과의 적합도를 검증하기 위해 기존 문헌에서 상수도 관망 해석의 예제로 사용된 가상의 관망 시스템에 대해 정상 및 비정상상황에 대한 수리해석을 수행하였고, 그 결과를 기존 DDA 및 PDA 모형과 비교하였다.

비교 결과, 제안된 A-PDA는 각 시간대 별 유한수원의 저류량 변화에 따른 수위를 고려하여, 해당 수위를 기준으로 각 절점의 수압과 공급가능 유량을 산정하며, 이에 따라 수원의 저류량과 절점의 수압을 동시에 고려한 수리해석 결과를 도출할 수 있다는 것을 확인 할 수 있었다. 나아가 특정 수원을 통한 유량 공급에 문제가 발생한 비정상상황에 대한 모의 결과, 기존 DDA 및 PDA 모형에서는 무한수원 가정에 의해 일정한 유량이 상수도 관망 시스템 전반에 걸쳐 지속적으로 공급되는 것과 달리, A-PDA 모형에서는 비정상상황 발생시 시스템에 유량이 공급 가능한 시간이 산정 가능하므로, 실무적인 측면에서 운영자의 보다 효과적인 의사결정을 지원할 수 있을 것으로 기대된다.

한편, 본 연구에서는 A-PDA의 적용성을 평가하기 위해 비교적 작은 규모의 가상 관망을 그 대상으로 하였으나, 향후 연구에서는 실제 국내외 대규모 상수도 관망 블록 시스템의 비상시 수계전환 평가 등에 적용하여 다양한 비정상상황에 대한 시스템의 거동을 평가할 예정이며, 또한 수리학적 인자뿐만 아니라 수질적 요소에 대한 모의 및 결과 분석을 수행하여 개발 모형의 신뢰도와 실무적용성을 지속적으로 강화할 계획이다.

Article information Continued