Seismic Evaluation of Existing Earth-Cored Fill Dams based on Pseudostatic and FE-Newmark Approaches

DongSoon Park

doi:10.9798/KOSHAM.2016.16.4.215

J. Korean Soc. Hazard Mitig. > Volume 16(4); 2016 > Article

Park: Seismic Evaluation of Existing Earth-Cored Fill Dams based on Pseudostatic and FE-Newmark Approaches

지진방재

J Korean Soc Hazard Mitig 2016; 16(4): 215-225.

Published online: August 30, 2016

DOI: https://doi.org/10.9798/KOSHAM.2016.16.4.215

Seismic Evaluation of Existing Earth-Cored Fill Dams based on Pseudostatic and FE-Newmark Approaches

DongSoon Park^*

^*Corresponding Author. Member. Principal Researcher, K-water Institute, Korea Water Resources Corporation
(Tel: +82-42-870-7611, Fax: +82-42-870-7619, E-mail: fulgent@kwater.or.kr)

Received April 12, 2016 Revised April 15, 2016 Accepted May 16, 2016

Abstract

등가정적해석은 댐의 지진 시 사면 안정성을 평가하기 위한 방법으로 여전히 널리 사용되고 있는 기법이다. 2011년 개정 댐설계기준에 의하면 등가정적 지진계수값은 설계 PGA의 약 70% 수준을 채택하고 있으며, 허용 안전율은 1.2를 취하고 있다. 그러나 댐의 성능을 지배하는 것은 영구 변형량이라 할 수 있다. 본 연구에서는 국내의 기존 21개 중심코어형 필댐에 대하여 개정 기준을 적용한 내진성능 평가를 수행하였다. 등가정적해석과 유한요소법 및 Newmark 변형해석을 수행하여 등가정적 지진계수와 허용 안전율의 타당성에 대해 검토하였다. 해석을 위해서 등가정적 한계평형해석과 더불어 정상침투 해석, 등가선형 지진동 해석 및 Newmark 변형 해석을 차례로 적용하였으며, 최신 물리탐사 기술을 적용한 전단파속도 주상도를 구하여 현장의 동적물성을 반영한 평가를 수행하였다. 연구 결과, 현재의 등가정적 지진계수와 허용 안전율 채택 기준은 대단히 보수적인 것으로 판단되었으며 향후 기준 개정시 이에 대한 고려가 필요할 것으로 검토되었다. 유한요소 및 Newmark 변형해석 결과, 기존 필댐들은 상향된 내진성능을 모두 만족하였으며, 추가적인 민감도해석을 통해 지진파의 증폭 양상, 임계 활동면의 위치, 쉘존의 내부마찰각 등이 영구 변형량에 지배적인 영향 인자로 판명되었다.

핵심용어: earthquake, dynamic analysis, seismic evaluation, fill dam, Newmark deformation, slope stability, earth cored fill dam

핵심용어: 지진, 동해석, 내진평가, 필댐, Newmark 변형, 사면안정, 중심코어형 필댐

요지

The pseudostatic approach is still in widespread use in industry to evaluate seismic slope stability of dams. According to the revised seismic design guideline of dams in Korea (2011), the pseudostatic seismic coefficient for dams is defined as about 70% of design PGA, and an allowable factor of safety (FS) is taken as 1.2. However, in terms of serviceability, permanent deformation matters rather than the FS. In this study, the seismic safety of 21 existing earth-cored fill dams in Korea was re-evaluated using updated design criteria. Accordingly the suitability of pseudostatic coefficient and allowable FS was studied. A systematic procedure was applied in a row of pseudostatic limit equilibrium analyses, steady state FE (finite element) seepage analyses, equivalent-linear dynamic response analyses, and Newmark type deformation analyses. In order to reflect in-situ dynamic soil properties as input parameters, innovative in-situ shear wave velocity profiles were adopted using up-to-date geophysical surveys. A comparison between pseudostatic limit equilibrium and FE-Newmark deformation analyses yielded that for a pseudostatic method with horizontal seismic coefficient of 70% design PGA and the allowable FS of 1.2 were found to be significantly conservative, which is believed to be considered in the revision of design guideline in the future. As a result of FE-Newmark type analyses, existing earth-cored fill dams showed a reasonably satisfactory performance under the updated design PGA. Additional sensitivity analyses showed that the amplification of ground motion within the sliding mass, the location of critical slip surface, and the internal friction angle of shell materials are the dominant factors governing permanent displacements.

핵심용어: earthquake, dynamic analysis, seismic evaluation, fill dam, Newmark deformation, slope stability, earth cored fill dam

핵심용어: 지진, 동해석, 내진평가, 필댐, Newmark 변형, 사면안정, 중심코어형 필댐

1. Introduction

Korea is known as relatively low to medium seismicity area. However, recent devastating earthquakes occurred in Japan and China (2011 M 9.0 Tohoku earthquake, and 2008 M 7.9 Wenchuan earthquake) and associated damages in existing dams and appurtenant structures (USSD, 2014; Wieland, 2012; Matsumoto and Sasaki, 2012; Matsumoto et al., 2012; Hinks et al., 2012) have facilitated a research for seismic analyses of existing fill dams in Korea. Under this research program, the seismic safety of existing large fill dams in Korea was re-evaluated using higher design PGA (peak ground acceleration) and updated numerical approaches specified in the revised seismic design code in Korea (KWRA, 2011).

According to the Korean seismic dam design code updated in 2011, a basic method still adopts pseudostatic approach based on pseudostatic limit equilibrium analysis. The allowable factor of safety (FS) for pseudostatic approach is 1.2. The revised guideline also suggests dynamic analyses in lieu of serviceability of dams. For dynamic analyses of large dams, Newmark type approach is adopted as a fundamental approach. Allowable plastic deformation for seismic safety is defined as 30 cm for no functional problem in dam safety, and 60 cm for accompanying allowable damage of dams.

Selecting design ground motion for these two approaches based on the guideline is complicated because pseudostatic and dynamic approaches use different input values. Due to the nature of conservatism for pseudostatic approach, the horizontal seismic coefficient (k_h) of pseudostatic approach is taken lower than the PGA of dynamic analysis. Assuming medium rock mass foundation, k_h is typically taken as 0.154 and 0.11 for seismic class, “S” and “I”, respectively. However, PGA values for dynamic analyses are taken as 0.22 g and 0.154 g for seismic class, “S” and “I”, respectively. In other words, the design coefficient values for pseudostatic approach are taken about 70% of those for dynamic approach, according to the updated seismic design guideline. Note that seismic class, “S” in Korea corresponds to multi-purpose dams, and dams of height greater than 45 m and reservoir capacity greater than 50 million m³. All other large dams fall in to seismic class “I”. The corresponding return periods of seismic class, “S” and “I” are 2,400 years and 1,000 years, respectively.

The discrepancy of the input values leads to the study of the appropriateness of seismic coefficient and design PGA between pseudostatic and dynamic analyses. This study also includes a review correlating with allowable seismic safety criteria, which is represented by either factor of safety or plastic deformation.

On the other hand, due to increased seismic demand according to the design guideline, re-evaluation of existing large fill dams needs to be studied for ensuring seismic safety. A part of the study was published by Park (2014) including seismic evaluation of existing four fill dams first. This paper significantly extends the cases of seismic evaluation up to 21 earth-cored fill dams with more enhanced dynamic material properties.

For the above main purposes, in this paper, pseudostatic and FE (finite element) – Newmark type dynamic analyses were conducted for 21 existing cored fill dams. All dams used in this study have been operated safely without any incidents of failure or significant water release since their end of construction. Therefore, all dams are statically safe under normal operation currently.

Comprehensive geophysical surveys were also performed in order to obtain dynamic material properties, which were incorporated into dynamic analyses. Based on pseduostatic and dynamic analyses, the result is discussed in terms of a factor of safety and seismic serviceability, i.e., deformation.

In addition, critical review to select seismic coefficient of pseudostatic method is stated based on the findings of this study. Other important characteristics are discussed and concluded such as the propagation of ground motion through dam body, critical factors of Newmark type approach in conjunction of plastic deformation. Suggestions in times of revision of seismic design code are made at the end.

2. Literature Review

2.1 Pseudostatic Analysis

Since the updated seismic design guideline for dams in Korea (2011) still adopts the pseudostatic approach as a basic approach, it is important to discuss the suitability of criteria. According to Kramer (1996), pseudostatic analyses can be unreliable for soils that build up high pore pressures ratio or show more than about 15% degradation of strength because of shaking. Terzaghi (1950) mentioned that the pseudostatic method is very inaccurate and a slope could be unstable even if the computed FS is greater than 1. In FEMA-65 (2005), it is stated that a pseudostatic approach should only be considered as an index of the seismic resistance and the approach cannot predict failure, which means that other types of analysis are generally required to provide a more reliable outcome.

Another challenging issue is to choose appropriate (horizontal) seismic coefficient (k_h). Current seismic design guideline for dams in Korea specifies to use k_h value as about 70% of design PGA.

Fell et al. (2005) stated that because the pseudostatic method assumes that the k^h acting on the potentially unstable mass is permanent and in one direction only, it can be unreliable. In reality, the state of FS to drop below one exists only for a short time. In recognition of the fact that actual slopes are not rigid and that the peak acceleration (a^max) exists for only a very short time, pseudostatic coefficients used in practice generally correspond to acceleration values well below a^max of design ground motion. The assumption of k^h = PGA leads to a very uneconomic evaluation and possible numerical difficulties for k^h ≥ 0.4 (Abramson et al., 2002).

It seems clear that k_h should correspond to some fraction of the anticipated peak acceleration. Kramer (1996) stated that although engineering judgment is required, the criteria of Hynes-Griffin and Franklin (1984) should be appropriate for most slopes. Hynes-Griffin and Franklin (1984)’s recommendation is that earth dams with FS greater than 1.0 using k_h = 0.5 a_max/g would not develop “dangerously large” deformations. This philosophy was also adopted by the US Corps of Engineers (1982). They recommended the use of a k_h to (1/2)*PGA for FS of 1.0 and the use of undrained conditions for cohesive soils and drained conditions for free draining granular materials, with a 20% strength reduction to allow for strain weakening during the earthquake loading. If a dam failed to satisfy this, they recommended more accurate and detailed analyses (Fell et al., 2005).

Note should be taken that it is meaningful to correlate pseudostatic FS with permanent deformation because seismic serviceability of fill dams is actually governed by deformation. Recently Bray and Travasarou (2009) suggested a reasonable basis for selecting the seismic coefficient in conjunction with seismic displacement judged to be allowable.

2.2 Newmark Type Analysis

Pseudostatic approach to producing FS does not give any information about serviceability during or after the earthquake. Serviceability can be represented as plastic deformation for dam body. Hence, pseudostatic method cannot tell freeboard deficiency of dams, but can tell yield acceleration of dam slopes and the location of critical slip surface. Yield acceleration is typically obtained by computing seismic coefficient that yields the FS equal to one. Thus, earthquake-induced permanent deformation needs to be checked using dynamic time history analyses for seismic safety evaluation. Dynamic analysis is a highly recommended way to account for serviceability of dam body.

Since limit equilibrium analysis has nothing to do with displacement, practically Newmark sliding block analysis is a useful tool to estimate permanent displacement on the potential sliding mass. The Newmark rigid sliding block analysis (Newmark, 1965) has been in widespread use to estimate earthquake- induced permanent displacement of fill dams because it is handy and physically reasonable. In conjunction with finite element (FE) dynamic analysis and pseudostatic limit equilibrium analysis, Newmark type deformation analysis produces predicted permanent deformation in case of no liquefaction potential and no significant strength degradation of dam materials. The basic principle of this method is that permanent displacement occurs if the acceleration of slope mass exceeds the static yield acceleration, a_y.

Despite of some unrealistic assumptions (Bray and Travasarou, 2009; Park and Kutter, 2009), ICOLD (2010) stated that the Newmark type dynamic analysis of the dam will serve as a basis to estimate permanent earthquake-induced displacements if the foundation and embankment materials are not susceptible to loss of stiffness and strength, or if the embankment is not saturated. Thus, in this study, pseudostatic analyses were firstly performed and plastic deformation is estimated by Newmark type deformation analyses after FE dynamic time history analyses in the sequel.

2.3 Components of Ground Motion

There have been continuous debates to use vertical component of ground motion in addition to horizontal component simultaneously. Gazetas (2012) mentioned that the simultaneous pseudostatic application of the peak of the horizontal and vertical components is a gross violation of the physics. It turns out that simultaneous application of the two complete time histories, the result are hardly different from those when only horizontal component is imposed mainly because of the nature of the two components whose frequency content and phasing details differ substantially, and hence they do not essential combine their effects (Gazetas et al., 2009; Sarma and Scorer, 2009). Therefore in this study, only horizontal seismic coefficient or horizontal acceleration time histories are taken into account (Kramer, 1996; ICOLD, 2010).

3. Numerical Modeling Procedure

The FE and Newmark type (FE-Newmark) dynamic analyses were conducted for 21 existing cored fill dams in Korea. A systematic procedure was applied in a sequence of steady-state FE (finite element) seepage analyses, equivalent-linear dynamic response analyses, and Newmark type deformation analyses (as shown in Park, 2014). Pseudostatic limit equilibrium analyses were also conducted in parallel. The software adopted was the GeoStudio (version 2012) that has sub-components of the module, SLOPE/W, SEEP/W, and QUAKE/W (Geo-slope International Ltd., 2012).

The constitutive models applied were the equivalent-linear model for the FE dynamic analyses and the Mohr-Coulomb model for pseudo-static and Newmark deformation analyses. Horizontal pseudostatic seismic coefficient, k_h was taken as 0.154 for seismic class, “S” dams, and 0.11 for seismic class, “I”. These values are equivalent to about 70% of PGA used in FE dynamic analyses.

3.1 Input Motions for FE Analyses

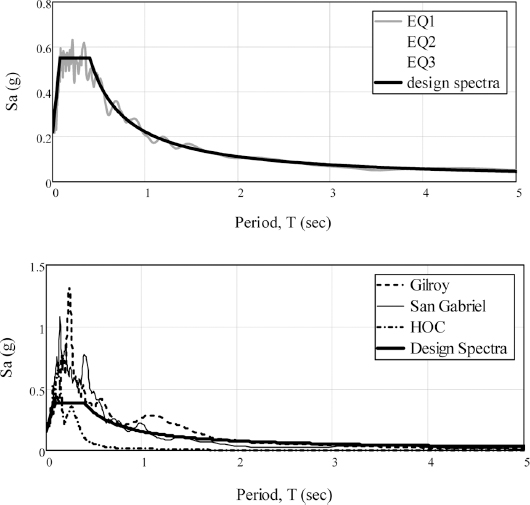
A total of six horizontal input motions were adopted for FE dynamic analyses. Three input motions were artificially synthesised according to the standard design response spectrum. Artificial earthquake time histories were made with durations of 15, 20, 25 sec (which are called “EQ1”, “EQ2”, and “EQ3”, respectively). Other three earthquake time histories that have a similar predominant period with the standard design response spectrum were also adopted. They were originally based upon measured records – “HOC” from the record at Hongcheon station for 2007 Ohdaesan earthquake (M 5.8), “Gilroy” from the record at Gilroy Array #6 station for 1989 Loma Prieta earthquake (M 6.93), and “San Gabriel” from the record at San Gabriel-E Grand Ave. station for 1994 Northridge earthquake (M 6.69). The shapes of response spectra for six input motions are shown in the Fig. 1.

Fig. 1

Comparison of standard response spectra with that of input motions applied.

The PGA of six input motions was scaled up to 0.22 g and 0.154 g depending on the seismic classification according to the Korea seismic dam design guideline.

3.2 Material Properties

Fundamental material properties such as strength parameters, hydraulic conductivity, and unit weight were adopted by design document or in-situ test which had been performed recently at each dam (K-water Institute, 2013; 2014). Table 1 shows some properties adopted for analyses. Internal friction angle (ϕ) of shell zone is ranged from 35 to 43 degrees with a median value of 38 degrees. For core layers, strength parameters, cohesion (c) and ϕ are ranged as 8−55 kPa and 19−39 degrees, respectively. The permeability of coefficient (k) of core layers is ranged as 1.0E-5−4.6E-7 cm/s.

Table 1

Dimensions and material properties of fill dams for dynamic analyses

Dam	Basic dimension					Shell zone
Dam	H (m)	US slope	US slope (deg.)	DS slope	DS slope (deg.)	γ_t (kN/m³)	φ (deg.)	G_max = f(σ’_vc)	G/G_max, ξ curve
SYG	122	1:2.3	23.5	1:2.0	26.6	18.0	40.5	HWAW	Rollins et al. 1998, Gravel
HS	47.5	1:2.2	24.4	1:1.8	29.1	18.9	41	HWAW	Rollins et al. 1998, Gravel
AD	81.7	1:2.0	26.6	1:1.7	30.5	21.8	43	HWAW	Rollins et al. 1998, Gravel
IH	65.2	1:2.2	24.4	1:1.8	29.1	18.8	42	Seed & Idriss 1970 Medium dense gravel	Rollins et al. 1998, Gravel
DC	35.6	1:2.0	26.6	1:1.8	29.1	19.6	41.4	HWAW	Rollins et al. 1998, Gravel
JAM	54.1	1:2.2	24.4	1:1.8	29.1	18.6	40	Seed & Idriss 1970 Medium dense gravel	Rollins et al. 1998, Gravel
JAR	89.6	1:2.2	24.4	1:1.5	33.7	18.6	40	Seed & Idriss 1970 Medium dense gravel	Rollins et al. 1998, Gravel
BR	47.5	1:2.2	24.4	1:1.9	27.8	18.6	41	SASW	Rollins et al. 1998, Gravel
GD	52.3	1:2.5	21.8	1:2.0	26.6	19.1	38	Seed & Idriss 1970 Medium dense gravel	Rollins et al. 1998, Gravel
DB	52.5	1:2.2	24.4	1:1.8	29.1	19.1	38	Seed & Idriss 1970 Medium dense gravel	Rollins et al. 1998, Gravel
YCN	42.5	1:2.7	20.3	1:2.5	21.8	19.6	35	MASW	Rollins et al. 1998, Gravel
GP	30.3	1:2.2	24.4	1:1.8	29.1	18.6	38	Seed & Idriss 1970 Medium dense gravel	Rollins et al. 1998, Gravel
WM	47.8	1:2.2	24.4	1:1.8	29.1	21.1	37	MASW	Rollins et al. 1998, Gravel
SY	41.8	1:2.0	26.6	1:2.0	26.6	18.6	38	SASW	Rollins et al. 1998, Gravel
DA	26.0	1:2.0	26.6	1:3.0	18.4	19.0	38	Seed & Idriss 1970 Medium dense gravel	Rollins et al. 1998, Gravel
YC	24.0	1:2.7	20.3	1:2.0	26.6	17.3	38	Seed & Idriss 1970 Medium dense gravel	Rollins et al. 1998, Gravel
GC	51.0	1:2.5	21.8	1:2.0	26.6	19.6	38	SASW	Rollins et al. 1998, Gravel
SO	63.6	1:2	26.9	1:1.8	29.1	18.4	38	MASW	Rollins et al. 1998, Gravel
PL	31.0	1:2.2	24.4	1:2.2	24.4	20.0	39	Seed & Idriss 1970 Medium dense gravel	Rollins et al. 1998, Gravel
AG	31.8	1:3.2	17.4	1:2.5	21.8	20.6	35	Seed & Idriss 1970 Loose sand	EPRI 1993, Sand
SA	24.4	1:2.0	26.6	1:3.2	17.4	19.0	38	Seed & Idriss 1970 Medium dense gravel	Rollins et al. 1998, Gravel

Note, US = upstream, DS = downstream, γ_t = total unit weight, φ = internal friction angle, G = shear modulus, G_max = maximum shear modulus, σ’_vc = vertical effective stress or vertical overburden pressure, ξ = damping ratio curve as a function of shear strain.

Dynamic soil properties are of utmost importance to evaluate the seismic performance of fill dams composed of different soil layers. The main dynamic material property was the shear wave velocity (Vs), which represents the stiffness of dam body. For enhancement of reliability of dynamic analyses, in-situ Vs profile measurements were conducted such as SASW (Spectral Analysis of Surface Waves), MASW (Multi-channel Analysis of Surface Waves), and HWAW (Harmonic Wavelet Analysis of Waves). Vs profile was later converted to maximum shear modulus (G_max) profile, which is a function of effective overburden pressure, σ’_vc. If there is no known geo-physical survey data obtained before, typical built-in material properties in QUAKE/W (version 2012) were adopted for analyses.

Other important dynamic material properties for equivalent linear dynamic analyses are shear modulus curve and damping ratio curve depending on the shear strain. For reasonable applications, Rollins et al. (1998)’s curve was mainly used for nonplastic gravelly materials, and Vucetic and Dobry (1991)’s curve was used for the plastic core layer.

More detail information regarding analyses procedure, input parameters, and input motions are shown in Park (2014) and Kwater Insitute (2013; 2014).

3.3 Outline of Analyses Conditions

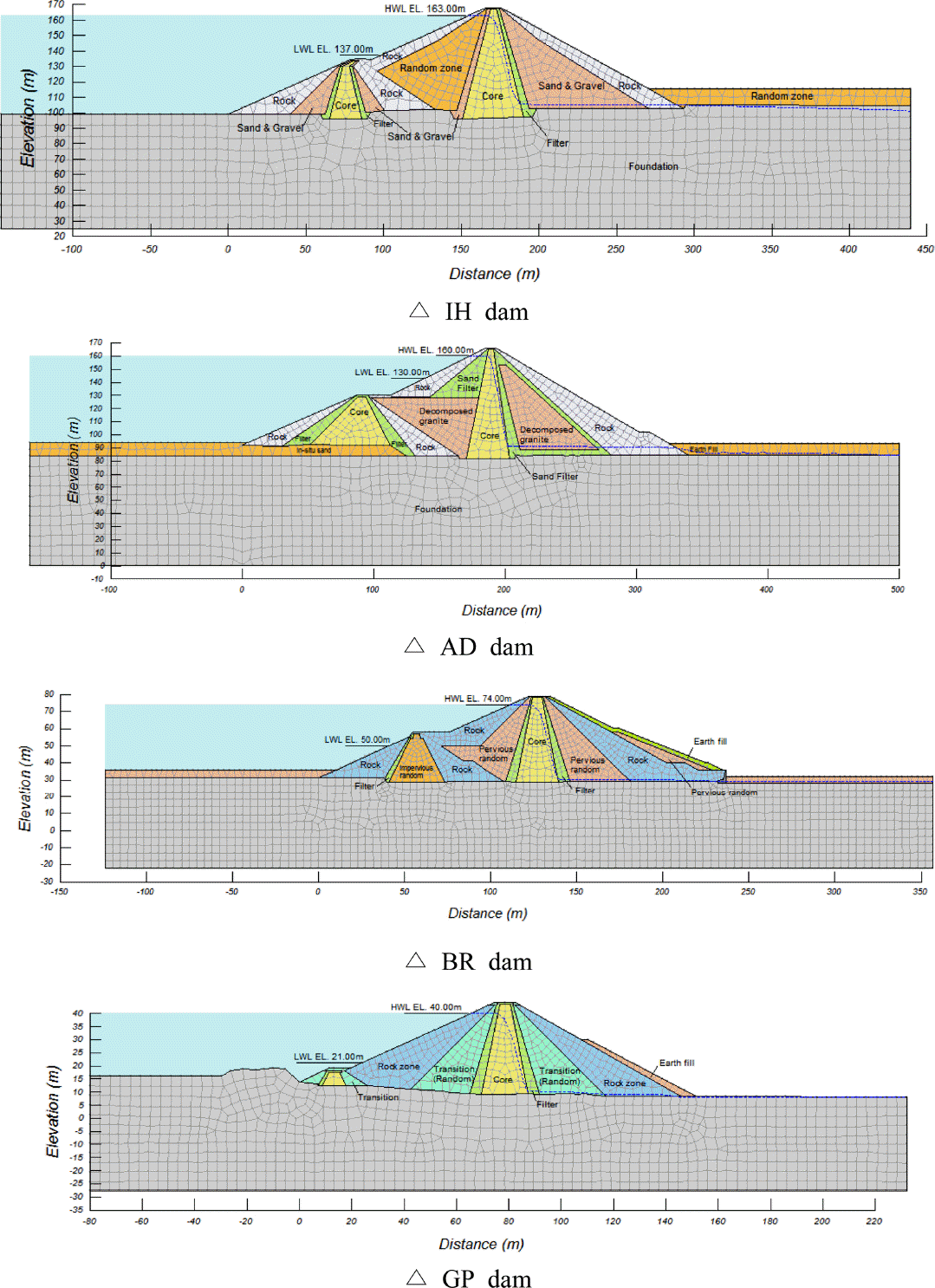
Table 1 shows model conditions and material properties for the dams analyzed. Fig. 2 shows typical geometry, zoning, and phreatic lines of four dams out of 21 earth cored fill dams as a result of steady-state seepage analyses. All dams used in the study largely comprises of the central core, filter, and shell layers.

Fig. 2

Typical cross-sections of some dams used in the study

For steady-state seepage analyses, normal high water level (NHWL) was used. Since seepage analyses have a significant effect on the result of pseudostatic analyses for upstream slope, fully saturated permeability coefficient in conjunction with typical soil-water characteristic curve for compacted cores were carefully selected based on laboratory tests for most cases.

Existing cored fill dams typically have the upstream slope of 1:2.0 to 1:3.2 (median = 1:2.2, 24.4 degrees), and the downstream slope of 1:1.7 to 3.2 (median = 1:1.9, 27.8 degrees).

Newmark type deformation analysis are conducted with FE dynamic analysis (QUAKE/W) and pseudostatic analysis (SLOPE/W). The basic computation procedure of permanent displacement comes from the double integration of the area under the average acceleration where the acceleration exceeds yield acceleration (a_y) on the potential sliding surface. Yield acceleration is defined as the average acceleration corresponding to a factor of safety of 1.0. The average acceleration of the potential sliding mass is obtained by dividing the total mobilized dynamic shear force by the mass. And the total dynamic shear force is the integration of dynamic stress (= stresses from QUAKE/W – initial in-situ static stresses) along the entire slip surface (Geo-slope International Ltd., 2012).

4. Result

A summary of result for pseudostatic and dynamic analyses is shown in Table 2. In Table 2, FS_all means the allowable factor of safety; AveD is the average permanent displacement obtained by FE-Newmark analysis; k_y is the yield acceleration coefficient, which is computed as a horizontal seismic coefficient (k_h) to yield FS of one.

Table 2

A result of dynamic and Newmark deformation analyses for cored fill dams

Dam	Pseudostatic analyses			FE analyses		Newmark deformation			Slip surface location
Dam	k_h	FS	FS_all	PGA (g)	a_max ratio	k_y	D (cm)	Ave D (cm)	Slip surface location
SYG	0.154	0.980	1.2	0.22	2.1-4.2	0.200	7.5-17.0	15.9	local
HS	0.154	1.022	1.2	0.22	2.4-3.5	0.196	1.7-8.3	5.3	local
AD	0.154	1.057	1.2	0.22	2.2-3.3	0.170	4.3-20.9	8.2	local
IH	0.154	0.999	1.2	0.22	2.3-2.6	0.190	13.9-25.4	19.6	local
DC	0.154	0.953	1.2	0.22	2.6-3.4	0.192	1.8-4.0	3.0	global
JAM	0.154	0.969	1.2	0.22	2.1-4.4	0.193	13.5-35.4	24.7	local
JAR	0.154	0.966	1.2	0.22	3.1-6.6	0.185	0.0-1.5	0.6	global
BR	0.154	1.058	1.2	0.22	2.7-6.6	0.234	11.6-29.5	21.1	local
GD	0.11	1.198	1.2	0.154	3.4-4.6	0.197	2.9-7.6	5.0	local
DB	0.11	1.121	1.2	0.154	2.3-2.8	0.178	1.0-3.1	1.7	local
YCN	0.11	1.140	1.2	0.154	2.8-3.9	0.177	1.0-9.8	2.1	local
GP	0.11	1.085	1.2	0.154	3.6-3.9	0.180	1.8-5.7	3.3	global
WM	0.154	0.980	1.2	0.22	3.9-5.5	0.206	7.9-27.8	10.5	local
SY	0.11	0.969	1.2	0.154	3.1-3.8	0.143	5.8-12.7	11.0	local
DA	0.11	1.093	1.2	0.154	3.5-4.3	0.202	9.3-28.5	10.2	local
YC	0.11	1.208	1.2	0.154	2.6-3.8	0.180	4.6-15.8	9.7	local
GC	0.11	1.240	1.2	0.154	3.7-4.8	0.238	0.6-2.2	0.7	local
SO	0.11	1.021	1.2	0.154	2.5-3.9	0.154	6.4-16.1	7.1	local
PL	0.11	1.168	1.2	0.154	3.6-4.4	0.214	2.4-6.3	3.1	local
AG	0.11	1.256	1.2	0.154	2.7-3.2	0.210	1.9-10.1	3.0	local
SA	0.11	1.270	1.2	0.154	3.1-4.1	0.179	0.0-0.9	0.2	global

For pseduostatic and dynamic analyses, upstream slopes are more vulnerable to deform dynamically than downstream slopes since the upstream portion of dam body is mostly saturated, hence, existing pore pressure yields effective stress decrease because of reservoir water induced steady-state seepage. Thus, the factor of safety and permanent deformation computed in Table 2 was taken from the upstream slope side.

Fig. 3 displays various correlations that were attempted to make among characteristic parameters (e.g., height, slope angle, natural frequency, friction angle, yield acceleration, etc). Some plots show a correlation between each influencing factor, but many plots show that there is no clear trend or unique relationship between parameters. Note that in Fig. 3, H is the height of a dam; FS is the factor of safety computed by pseudostatic limit equilibrium analysis; US slope is the upstream side slope; AFR is the amplification ratio between the peak acceleration on the dam crest and PGA of the input motion; T_n is the natural period which produces the maximum ratio of acceleration response spectra on the crest divided by that on the foundation; f_n is the natural frequency (=1/T_n); and shell φ is the friction angle of shell material.

Fig. 3

Plots showing results of pseudostatic and FE-Newmark analyses for existing cored fill dams in Korea

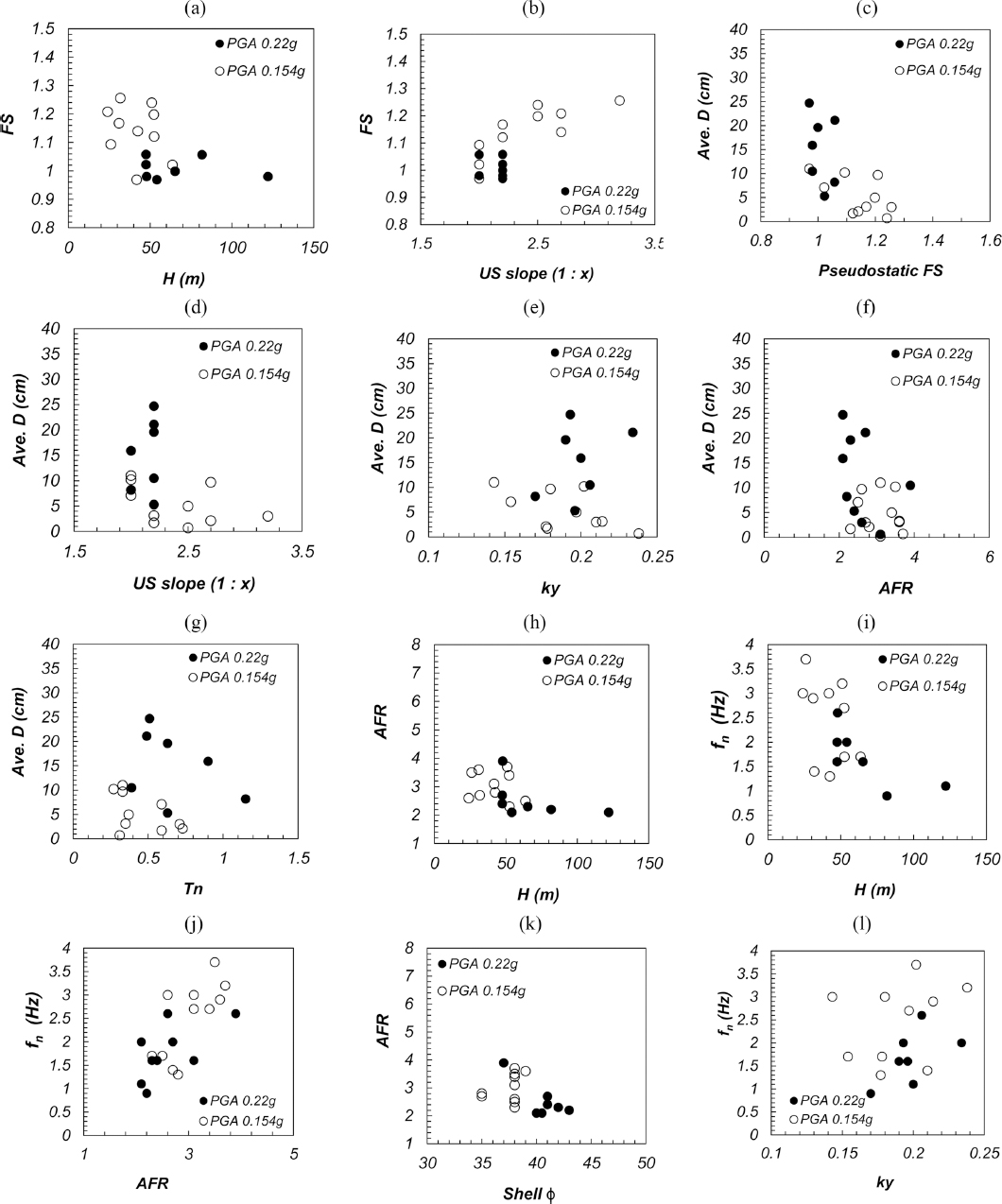
For pseudostatic analyses, when we set up allowable FS as 1.2, and horizontal seismic coefficient (k_h) as approximately 70% of PGA values for dynamic analyses, we obtained mostly unsatisfactory FS less than 1.2 (Fig. 3(a)). For many cases, FS was marginally close to 1.0. As expected, seismic class “S” dams show typically lower FS than seismic class “I” dams because of less k_h values. Fig. 3(a) does not exhibit a unique relationship between H (= height of dam) and FS. But in general, FS increases as the US (upstream) slope increases (Fig. 3(b)). If there is no serviceability calculation, which can be represented by permanent deformation on potential slip surface, then the pseudostatic computation leads to an unstable state of dams for seismic demand defined in the national seismic design guideline (KWRA, 2011).

However, as a result of dynamic FE and Newmark deformation analyses for upstream slope-side, average permanent deformation was found to be 0.2 cm to 24.7 cm (mean value of 7.9 cm, the median value of 5.3 cm) only (Fig. 3(c)). In Korea, the safety criterion for Newmark deformation of fill dams is guided as 30 cm for the condition of no damage. In view of this criterion, all evaluated fill dams may be safe under the design PGA in Korea.

Fig. 3(c) shows the plot of permanent displacement versus pseudostatic FS. Though there is significant scatter, it is shown that the permanent displacement roughly decreases as pseudostatic FS increases. It should be noted that most fill dams show pseudostatic FS less than allowable FS (= 1.2), but average deformation is not significant. Thus, pseudostatic FS may be the somewhat over-conservative approach. The real serviceability of dams after the earthquake should be evaluated by permanent deformation. In this regard, a selection of k_h as about 70% of PGA for seismic evaluation of cored fill dams can produce a significantly over-conservative result.

Figs. 3(d) to 3(g) indicate that D (= permanent Newmark deformation) has no unique relationship with respect to the upstream slope angle, k_y, AFR, and T_n. The main reason of this might be complicated nature among these influencing factors on the result. The results of dynamic analyses are not governed by a single dominating factor, but by multiple factors (Park and Kutter, 2009).

Figs. 3(h) to 3(l) exhibit different characteristic relationships of other combination plots. Fig. 3(h) roughly shows that the peak acceleration of lower height dams relatively amplifies more than higher dams. Amplification ratio varies from 2 to 7 approximately, mostly being 2 to 3.

According to the JCOLD data (JCOLD, 2014) which has been collected from measured dam acceleration time histories through 1978 to 2013, the amplification ratio of dam crest and foundation (or ground) is ranged about 1 to 6 for PGA of 0.154 g, but less than 2 for PGA of 0.22 g (Fig. 4). The amplification ratio obtained from FE analyses seems a little higher than the measured one, but generally in reasonable agreement with field data, which verifies the validity of FE analyses on one side.

Fig. 4

A relationship between PGA and AFR (amplification ratio) based on measured strong motion data for fill dams in Japan (data from JCOLD, 2014). Note that CFRD is the concrete faced rockfill dam, and AFRD is the asphalt concrete faced rockfill dam.

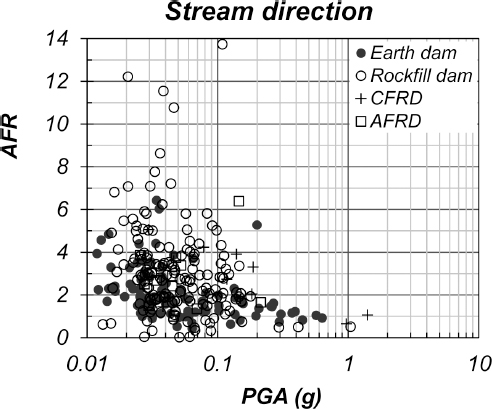
Fig. 3(i) is of interesting plot to show natural frequency decreases as the height of dam increases in overall. Considering all dams evaluated are cored fill dams, higher dams seem to accommodate lower natural frequency (longer natural period). Fig. 3(j) is the plot of natural frequency and amplification ratio. There is a trend that natural frequency gets higher as the peak acceleration amplifies more. Fig. 3(k) is the plot to attempt correlate amplification ratio with friction angle of the shell. Though there is not clear correlation, it seems higher friction angle of the shell makes relatively lower amplification of shaking. Lastly, Fig. 3(l) is the plot of the natural frequency of dams versus yield acceleration coefficient, which shows significant scatter of data.

In summary, all 21 existing fill dams are believed to be “safe” for seismic demand in terms of serviceability according to the updated guideline in Korea in 2011 whereas most fill dams are less than an allowable factor of safety in terms of pseudostatic slope stability for the seismic coefficient of about 70% of design PGA values. Since analyses results are based on in-situ measurement of shear wave velocity profiles by geophysical surveys and reliable literature empirical regression, as well as reasonable amplification ratio and reasonable natural frequency range, FE-Newmark analyses in this study will be useful reference for future revision of seismic dam design guideline, specifically for the selection of seismic coefficient and allowable factor of safety for pseudostatic approach.

5. Discussion

During the FE-Newmark analyses used in this study, influencing factors affecting permanent displacement and factor of safety are found such as the friction angle of the shell, the location of critical slip surface, dynamic material properties, input motions, the time interval to be saved, mesh size, and two-way sliding mechanism.

For Newmark type analysis, a friction angle of the shell was the core material property that governed deformation. And it impacted yield acceleration of the system directly. Yield acceleration is a sort of resistance of potential sliding mass.

Average acceleration on the slip surface can be a lot different whether it is locally or globally distributed (Table 2). Slip surface located in the upper part of upstream slope (dam crest ~ coffer dam crest) relatively yielded higher average acceleration on the potential slip surface, which produced relatively larger deformation.

Depending on the different combination of dynamic properties, deformation can be different. Therefore, it may be essential to conduct a site investigation to find the right Vs profile and/or to reasonably assume these properties.

It is clear that input motions affect the resulting deformation. More numbers of an acceleration exceeding k_y will yield more deformation.

Since Newmark type analysis used the technique of double-integration of acceleration time history beyond the yield acceleration, the consequential deformation was affected by the setup of the time interval of FE analyses.

During FE analyses and subsequent Newmark analyses, the final result could be different depending on the coarseness or fineness of the mesh generated.

Lastly, as fill dam is typically inclined upstream and downstream, conceptually deformation computation should occur both ways rather than one way. In this case, two-way sliding would be more reasonable than one-way sliding (Park and Kutter, 2009). When we think about two-way sliding, there should be two components of yield acceleration, positive and negative yield acceleration. As a result of computation of permanent displacement, two-way sliding displacement should be always equal or less than the single sliding displacement. One-way sliding block analysis never catches the up and down fluctuation of slope deformation. Therefore, two-way sliding block analysis might be a better way to predict slope displacement. But in this study, one-way sliding was just adopted for simplicity.

In the future, the above considerations, as well as the degree of conservatism between pseudostatic FS and dynamic deformation, need to be reflected in the revision of seismic design criteria.

6. Conclusion

According to the revised seismic design guideline of dams in Korea (2011), pseudostatic seismic coefficient for dams is defined as about 70% of design PGA and an allowable factor of safety is taken as 1.2. However, because what dominates the seismic safety of existing dams is not the factor of safety, but the permanent deformation, appropriateness of pseudostatic seismic coefficient and an allowable factor of safety should be discussed based on dynamic analyses to compute plastic deformation of dams.

In this study, seismic analyses for 21 existing earth-cored rockfill dams in Korea were conducted using a revised seismic design guideline of dams (KWRA, 2011). The analyses methods include pseudostatic limit equilibrium, finite element, and Newmark type deformation analyses. The design PGA for dynamic analyses was 0.22 g and 0.154 g depending on the seismic class. In order to reflect up-to-date dynamic soil properties (Vs), in-situ shear wave velocity profiles were measured through nondestructive geophysical surveys. A comparison between pseudostatic limit equilibrium and FE-Newmark deformation analyses were performed. The following conclusions were drawn.

Consequently, all existing earth-cored fill dams were believed to be safe in view of serviceability (i.e., deformation) under the revised design PGA and given input motions. Well-compacted earth cored fill dams in Korea is believed to be resistant to the design seismic demand of 0.22 g and 0.154 g as design PGA.

It is observed that pseudostatic approach with k_h of about 70% design PGA and allowable FS of 1.2 typically was significantly conservative. Most existing fill dams did not satisfy the FS criteria. In terms of permanent deformation, FS of 1.1 yielded to be dynamically stable, and even FS of 1.0 can be safe based on the FE-Newmark deformation analyses. Since permanent deformation based on the FE-Newmark type analyses was not significant, current over-conservatism need to be re-considered for a future revision of safety criteria for pseudostatic approach.

Pseudostatic method alone might not appropriate for seismic safety evaluation of fill dams, and dynamic analysis including deformation prediction needs to be more prioritized.

Additional sensitivity analyses showed that the amplification of ground motion on the sliding mass, the location of critical slip surface, and the internal friction angle of shell materials are the dominant factors governing permanent displacements.

Acknowledgement

This research was partially conducted by the research project, A Study on the Integrity Assessment of Aging Dams for Dam Performance Improvement, funded by K-water. Also, this research was partially funded by the KAIA (Korea Agency for Infrastructure Technology Advancement) research project, Development of Initiative Technologies for Remediation of Deteriorated Fill-dams using Smart Grouting and Effectiveness Verification System. The authors are grateful for the support.

References

Abramson, L.W, Lee, T.S, Sharma, S, and Boyce, G.M (2002). Slope stability and stabilization methods. John Wiley & Sons.

Bray, J.D, and Travasarou, T (2009) Pseudostatic coefficient for use in simplified seismic slope stability evaluation. Journal of Geotechnical and Geoenvironmental Engineering, ASCE, Vol. 135, No. No. 9, pp. 1336-1340. 10.1061/(ASCE)GT.1943-5606.0000012.

Fell, R, MacGregor, P, Stapledon, D, and Bell, G (2005). Geotechnical engineering of dams. CRC Press.

FEMA (2005) Federal guidelines for dam safety - Earthquake analyses and design of dam. FEMA-65, Federal Emergency Management Agency USA.

Gazetas, G (2012). Some presumptions on the nature of base excitation may erroneously affect the response of strongly inelastic systems. Proceedings of the 15th World Conference on Earthquake Engineering, Lisboa, Portugal.

Gazetas, G, Garini, E, Anastasopoulos, I, and Georgarakos, T (2009) Effects of near-fault ground shaking on sliding systems. Journal of Geotechnical and Geoenvironmental Engineering, Vol. 135, No. No. 12, pp. 1906-1920. 10.1061/(ASCE)GT.1943-5606.0000174.

Geo-slope International Ltd (2012) Stability modeling with SLOPE/W, An engineering methodology.

Hinks, J, Wieland, M, and Matsumoto, N (2012). Seismic behavior of dams. International Symposium on Dams for a Changing World, ICOLD Conference, Kyoto, Japan.

Hynes-Griffin, M.E, and Franklin, A.G (1984). Rationalizing the seismic coefficient method. Miscellaneous Paper No. G.L. 84-13. US Army Engineer Waterways Experiment Station, Vicksburg, Mississippi.

ICOLD (2010) Selecting seismic parameters for large dams guidelines. Committee on Seismic Aspects of Dam Design, International Commission on Large Dams.

JCOLD (2014) Acceleration records on dams and foundations, No. No. 3, The Japan Commission on Large Dams.

K-water Institute (2014). A study on the advanced seismic evaluation of existing dams (III), Final Report. 2015-WR-RR-7-16. Korea Water Resources Corporation.

K-water Institute (2013) A study on the advanced seismic evaluation of existing dams (II), Interim Report, KIWE-ISRC-13-02, Korea Water Resources Corporation.

Matsumoto, N, and Sasaki, T (2012). Effects of the 2011 Tohoku Earthquake on dams. International Symposium on Dams for a Changing World, ICOLD Conference, June 5, Kyoto, Japan.

Matsumoto, N, Sasaki, T, and Sato, N (2012). Effects of the 2011 Tohoku earthquake on dams. International Symposium on Dams for a Changing World, ICOLD Conference, Kyoto, Japan.

Newmark, N.M (1965) Effects of earthquakes on dams and embankments. Géotechnique, Vol. 15, No. No. 2, pp. 139-160. 10.1680/geot.1965.15.2.139.

Park, D.S (2014) A study on the seismic resistance of fill-dams by Newmark-type deformation analyses. Journal of Earthquake Engineering, EESK, Vol. 18, No. No. 4, pp. 161-170.

Park, D.S, and Kutter, B.L (2009) Discussion of “Analyzing liquefactioninduced lateral spreads using strength ratios”. In: Olson S.M, Johnson C.I, eds. Journal of Geotechnical and Geoenvironmental Engineering, ASCE, Vol. 135, No. No. 12, pp. 2008-2010. 10.1061/(ASCE)GT.1943-5606.0000101.

Rollins, K.M, Evans, M.D, Diehl, N.B, and Daily, W.D III (1998) Shear modulus and damping relationships for gravels. Journal of Geotechnical and Geoenvironmental Engineering, ASCE, Vol. 124, No. No. 5, pp. 396-405. 10.1061/(ASCE)1090-0241(1998)124:5(396).

Sarma, S.K, and Scorer, M (2009). The effect of vertical acceleration on seismic slope stability. International Conference on Performance based Design in Earthquake Geotechnical Engineering. In: Kokusho T, ed. Tokyo, Japan: p 889-905.

Seed, H.B, and Idriss, I.M (1970). Soil moduli and damping factors for dynamic response analyses. Report EERC 70-10, Earthquake Engineering Research Center, University of California, Berkeley.

KWRA (2011) Dam design guidelines. Korea Water Resources Association.

Kramer, S.L (1996). Geotechnical earthquake engineering. Prentice Hall.

Terzaghi, K (1950) Mechanisms of landslides. Geological Society of America, 10.1130/berkey.1950.83.

USACE (1982). Slope stability manual EM-1110-2-1902. Department of the Army, Office of the Chief of Engineers, Washington DC.

USSD (2014) Observed performance of dams during earthquake. US Society on Dams.

Vucetic, M, and Dobry, R (1991) Effect of soil plasticity on cyclic response. Journal of Geotechnical Engineering, ASCE, Vol. 117, No. No. GT1, pp. 89-107. 10.1061/(ASCE)0733-9410(1991)117:1(89).

Wieland, M (2012). Seismic design and performance criteria for large storage dams. 15th World Conference on Earthquake Engineering, Lisboa, Portugal.