2.1. 대상유역 및 강우관측자료

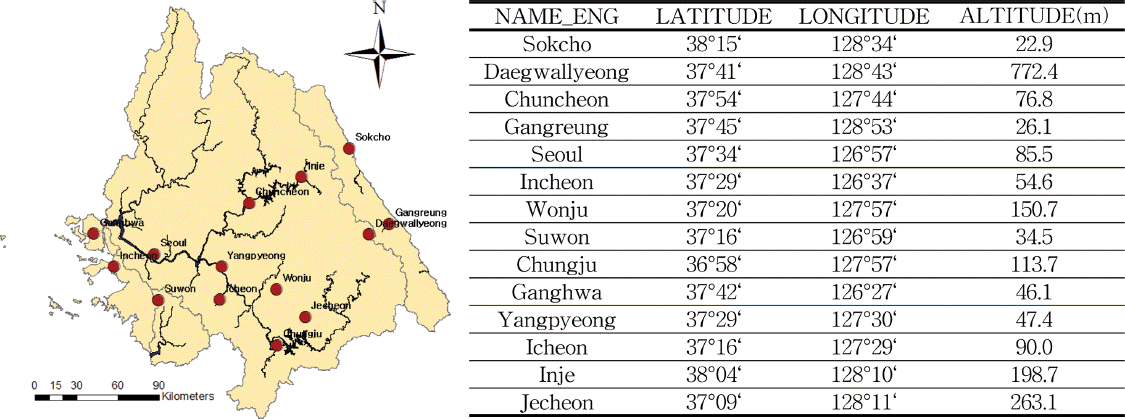
본 연구에서는 강우사상의 구조적인 변동을 분석하기 위하여 한강유역을 대상유역으로 선정하였다. 한강유역은 도시화면적이 넓고 인구가 밀집되어 있어 기후변화의 지역적 영향에 따른 강우의 변동이 미치는 영향력이 큰 유역으로 강우사상의 변동 분석이 필요한 유역이다. 한강유역의 면적은 북한에 위치한 면적을 포함하여 약 3만km² 이고 남한강을 본류로 남한강과 북한강으로 나뉜다. 팔당 하류의 김포평야와 일산평야는 범람원으로 형성된 평야이며 해발고도가 5-7 m에 불과하여 이상기후에 따른 집중호우의 증가로 피해가 증가하고 있으며 한강유역의 유량의 계절적 변화가 크다. 본 연구에서는 한강유역에 포함된 기상청에서 운영하고 있는 지상기상관측소(AWS, Automatic Weather System)중에서 30년 이상의 장기간 시단위 강우자료를 보유한 서울, 인천 등 14개소 지점을 선정하고 1973년부터 2014년까지의 시강우자료를 수집하여 연구를 수행하였다(Fig. 1).

Fig. 1

Study basin and weather stations.

2.2 추계학적 강우모형

본 연구에서는 추계학적 강우모형으로 수문학 분야에 널리 쓰이고 있는 NSRPM을 이용하였다. 수문학 분야에 널리 쓰이고 있는 NSRPM의 모형매개변수는 다섯 개의 확률분포로 이루어져 있으며 각 분포는 I.I.D(Independent Identically Distribution)이다. 각각의 분포는 강우사상의 발생시점과 각 강우사상과 결합하는 강우세포의 개수, 발생시점, 강우강도 및 지속시간을 나타낸다. NSRPM 구축은 다음과 같다. 강우사상의 발생시점(S)을 결정하기 위해 매개변수 λ를 가지는 지수분포를 이용한다(Eq. 1).

각각의 강우사상과 결합된 강우세포의 분포는 매개변수 μ를 가지는 기하분포(geometric distribution) 또는 지수분포를 따른다. 강수세포 수 N은 최소한 1개 이상 발생되어야 하므로 n=N-1로 가정한다. 따라서 n의 평균은 μ-1이며 N의 평균은 μ이다. 본 연구에서는 강우세포 개수 결정을 위해 기하분포를 이용하였다(Eq. 2). 강우세포의 발생시점은 지수분포에 의해 결정되며 매개변수β를 가진다(Eq. 3).

강우세포와 결합된 강우지속시간과 강우강도는 각각 매개변수 η, ξ를 가지는 지수분포를 이용하여 결정한다(Eq. 4, Eq. 5).

2.2.1 NSRPM의 통계적 특성

본 연구에서는 NSRPM의 모멘트를 이용하여 매개변수를 추정하였으며 Rodriguez-Iturbe et al.(1987)에 제시된 다섯개의 확률분포가 결합된 모멘트는 다음과 같다(Eq. 6-Eq. 8).

(6)E[Yi(h)]=λη−1μξh

(7)Var[Yi(h)]=λη−3(ηh−1+e−ηh)[4μξ2+2(μ2−μ)ξ2β2β2−η2]−λ(βh−1+e−βh)2(μ2−μ)ξ2β(β2−η2)

(8)Cov[Yi(h),Yi+k(h)]=λη−3(1+e−ηh)2 e−η(k−1)h[2μξ2+(μ2−μ)ξ2β2β2−η2]−λ(1−e−βh)2e−β(k−1)h(μ2−μ)ξ2β(β2−η2)

매개변수를 추정하기 위해 이용된 목적함수는 Cowpertwait et al.(1996)이 연구에 사용한 목적함수를 이용하였으며 지속시간 1시간 평균, 분산, 공분산과 지속시간 6시간 분산, 공분산 항을 이용하여 최소제곱오차를 구하였다(Eq. 9). 각 매개변수들의 추정범위는 다음과 같다(Table 1).

Table 1

Range of parameters for optimization

(9)minR=(1−E^(Yi(τ))E(Yi(τ)))2+(1−Var^(Yi(τ))Var(Yi(τ)))2+(1−corr^(Yi(τ),Yi+h(τ))corr(Yi(τ),Yi+h(τ)))2

2.3 매개변수 추정 기법

NSRPM의 매개변수를 추정하기 위해 유전자 알고리즘을 이용한 최적화 기법을 사용하였다. 유전자 알고리즘은 초기 부모세대를 무작위로 생성하여 적합도 평가를 통한 선택-교배-돌연변이-대치의 연산과정을 거쳐 최적해를 구한다. 유전자 알고리즘은 다윈의 자연선택 법칙 진화론을 기반으로 Holland(1975)에 의해 소개되었으며 경험적인 탐색을 통한 전역 최적해(global optima)를 구하는 기법이다. 유전자 알고리즘은 현실적으로 미분이 불가능한 비선형문제와 수식이 복잡한 목적함수의 최적화 기법으로 널리 쓰이고 있다. 유전자 알고리즘의 장점은 초기값이 필요하지 않으므로 사용자가 개입하여 초기조건을 설정하는 다른 기법보다 주관성의 개입이 적다. 또한 돌연변이 연산자에 난수생성, 비균등 변이 등 부모세대에 없는 속성을 도입하여 탐색공간을 넓힘으로써 지역해(local optima)를 피하는 구조를 가지고 있으며 많은 수의 부모세대를 생성함으로써 단일점이 아닌 다점(multi points)탐색이 가능하다. 그러나 적절한 적합도 함수의 선택과 부모세대의 크기, 교배와 돌연변이의 발생 확률의 결정이 필요하며 변이의 확률이 높아지면 탐색에 소요되는 시간이 오래 걸린다는 단점이 있다. 또한 다른 개체들 보다 월등히 우월한 개체가 존재하면 그 개체를 중심으로 교배, 변이가 발생하여 전체적으로 탐색하지 못하고 지역해에 수렴할 수 있다. 이러한 조기 수렴은 개체의 크기가 작을 때에도 발생한다. 최근에는 컴퓨터의 발전으로 연산속도가 향상되면서 유전자 알고리즘 사용이 증가하고 있는 추세이다. 일반적으로 적합도 평가를 통한 교배에 선택될 확률은 다음과 같이 계산된다(Eq. 10).

여기서 M_i는 i번째 개체의 적합도, M¯는 세대의 평균 적합도, P_(i)는 i번째 개체가 교배에 선택될 확률이다.

3.1 한강유역 강우변화 특성

한강유역의 14개 지점의 1973년에서 2014년 기간 동안에 호우일수 변동 추세를 분석하기 위하여 Mann-Kendall 추세분석 결과 속초, 대관령, 서울, 인천 지점은 신뢰수준 5%, 10%에서 모두 유의한 증가추세를 보였으며 이천지점에서는 신뢰수준 10%에서 유의한 증가 추세를 보였다. 강화지점을 제외한 나머지 모든 지점에서 증가추세를 보였다(Table 2).

Table 2

Mann-Kendall test of heavy rainfall day in the Han-River basin

유역의 평균 호우일수의 선형증가량은 약 1.2일로 서울 2.4일, 인천 2.1일, 춘천 1.7일 순으로 나타났다. 또한 1973년-1999년 동안의 호우일수와 2000년-2014년 동안의 호우일수의 평균을 비교한 결과에서도 증가추세를 보였다(Table 3).

Table 3

Change of heavy rainfall day and linear changes(day)

한강유역의 각 연도별 발생한 호우사상(80 mm/day)의 시간별 강우량을 이용하여 호우사상의 24시간 동안에 지속시간 3시간동안 발생한 최대 강우량 변동을 분석하였다. 본 논문에서는 강우의 지속시간 3시간을 강우집중시간으로 정의하였으며 강우집중시간(mm/3h) 동안 발생한 최대 강우량을 분석하였다. Table 3에서 살펴 볼 수 있듯이 수원, 충주 지점을 제외한 모든 지점에서 강우집중시간 동안의 강우량을 증가하는 추세를 보였으며 한강유역의 강우집중시간 동안의 평균 강우증가량은 약 7 mm/h로 나타났다. 지점별 증가량은 인제 20.5 mm/h, 서울 16.8 mm/h, 이천 16.1 mm/h 순으로 나타났다. 서울지점은 호우일수 증가와 강우집중시간의 강우 증가량에서 크게 나타났다. 또한 각 호우사상의 시간별 강우변동 특성 분석을 통해 시간대별 강우변동 특성을 분석하였다. 지속시간 24시간을 4분위로 나누어 지점별 강우변동 분석을 하였다. 서울 지점의 경우 1분위, 2분위에서 발생하는 강우량이 전체 강우량에서 가장 큰 비율을 차지했으며 4분위로 갈수록 강우량이 줄어든다. 그러나 무강우 시간은 1분위, 4분위에서 가장 많은 시간을 나타내어 1분위의 시간대에서는 강우의 발생빈도는 낮지만 높은 강우강도를 보였으며, 2분위에서는 높은 강우발생 빈도와 높은 강우강도, 3분위는 높은 강우발생빈도와 낮은 강우강도, 4분위는 낮은 강우발생빈도와 낮은 강우강도를 보였다. 전기(1973년-1999년)와 후기(2000년-2014년)로 두 기간 동안 호우사상 발생 횟수는 각각 69회, 51회 발생하였으며 2분위를 제외한 모든 분위에서 전기보다 후기에서 강우강도가 증가하였다. 시간대별 강우의 발생은 2, 3, 4분위에서 발생 빈도가 증가하였으며 1분위에서는 감소하였다. 한강유역 전체적으로는 1분위 강우강도가 감소하고 2분위 강우강도가 증가하는 것으로 나타났다.

3.2 한강유역 NSRPM 매개변수 추정 및 변동분석

한강유역 14개 지점을 대상으로 1973년-2014년 동안의 여름철 시강우 자료를 이용하여 연도별 NSRPM의 매개변수를 추정하고 생산된 강우특성 변화를 분석하였다. NSRPM의 매개변수 λ, μ, β, η, ξ는 순서대로 강우사상의 발생간격, 각 강우사상과 결합하는 강우세포의 개수, 강우세포의 발생간격, 강우세포의 지속시간, 강우세포의 강우강도를 의미한다. 서울지점의 1973년-2014년 기간 동안에 추정된 5개의 매개변수와 선형회귀 변화량은 다음과 같다(Table 4). Table 4에서의 Estimated와 Observed는 강우량을 의미한다. 한강유역의 평균 강우사상의 발생시간 간격은 0.0106 h^-1에서 0.0099 h^-1으로 약 -0.0007 h^-1의 변화량을 보였으며 강우사상의 시간간격은 7시간 증가하였다. 이는 최근 강우일수가 줄어들고 있는 추세를 반영하고 있으며 한강유역의 여름철 강우일수 변화는약 23회에서 21회로 감소하는 것을 보였다. 강우사상의 발생간격 시간이 가장 많이 증가한 지점은 강화 지점이며 강우사상 간격이 약 27시간 증가하였다. 강우사상의 발생간격이 가장 많이 감소한 지점은 속초지점으로 약 28시간 감소하였다. 강우사상과 결합하는 강우세포의 개수는 한강유역 평균 약35개로 증가하는 것으로 나타났으며 원주지점에서 증가량이 70개로 가장 큰 결과값을 보였으며 감소한 지점은 제천, 양평으로 두 지점 모두 강우세포 감소 수가 약 1.5개이다. 강우세포수와 밀접한 관계를 보이는 강우세포의 발생시간 간격은 한강유역 대부분에서 감소하였으며 평균 약 1.5시간 발생간격이 감소하였으며 가장 큰 폭으로 감소한 지점은 원주지점에서 약 5시간 감소하였다. 이는 원주에서 강우세포수가 가장 크게 증가한 것을 반영하는 결과이다. 한강유역의 평균 강우세포의 지속시간은 3.25 h^-1에서 2.83 h^-1으로 약 0.3시간 증가하여 강우사상의 지속시간이 증가하는 것으로 나타났으나 변화의 폭은 미미하였다. 강우세포의 지속시간이 가장 크게 증가한 지점은 원주이며 약 0.7시간이다. 지속시간이 가장 크게 감소한 지점은 인천으로 약 0.5시간 감소하였다. 강우세포와 결합하는 강우강도의 변화에서는 한강유역 평균 3.5 mm/h 감소하였으며 대부분의 지점에서 감소하는 결과를 나타냈다(Fig. 2). 강우강도는 감소하였으나 강우사상과 결합되는 강우세포 수의 큰 증가로 강우량이 증가하였으며 강우세포의 발생시간 간격이 감소함으로서 집중호우의 발생 가능성이 증가하는 결과를 보였다. 이는 최근 강우량의 증가와 호우일수 증가와 같은 강우의 변화 추세를 반영한다. 대표적 지점으로 서울지점은 강우사상간 발생시간 간격은 약 5시간 증가하였으며 강우세포의 개수는 약 35개 증가하였다. 각 강우세포간의 발생간격은 약 2시간 감소하였으며 강우세포의 지속시간은 0.2시간 증가로 지속시간의 변화는 미미 하였다. 강우세포의 강우강도는 약 3 mm/h 감소하였다.

Table 4

Parameter Estimation at the Seoul Station

Fig. 2

Linear change in parameters of NSRPM.

1973-1992년 기간 동안의 여름철(6월-8월) 강우자료를 이용하여 매개변수를 추정하고 강우를 1년씩 누적하여 2014년까지 매개변수를 추정하고 선형 회귀를 통하여 2044년의 매개변수를 추정하였다. 선형회귀 특성상 예측범위가 짧아 2014년부터 30년 후인 2044년을 선정하였다. 추정된 매개변수를 이용하여 1000년치의 강우를 생성하여 강우특성을 분석하였다. 분석결과 강우량과 호우사상의 강우량은 감소하였으며 호우일수 및 강우집중시간 동안의 강우량은 증가하였다. 여름강우량은 유역평균 약 37.9 mm 감소하였으며 호수사상의 강우량은 약 140 mm가 감소하였다. 호우일수는 유역평균 2.6일이 증가하였으며 강우집중시간 동안의 강우량은 13.4 mm증가하였다(Fig. 3, Fig. 4). 원주 지점에서 여름철 강우량이 가장 크게 증가하였으며 증가폭이 약 1000 mm이였다. 춘천지점에서 강우량이 약 크게 감소하였으며 약 550 mm 감소하였다. 호우일수 또한 원주지점에서 7.9일 증가하는 것으로 나타나 가장 큰 증가폭을 보였으며 인제 5.4일, 서울 5일 순으로 나타났다. 호우량은 전체 지점에서 100 mm-150 mm 증가를 보였으며 강우집중시간 동안의 강우량은 대관령에서 약 50 mm, 강릉 40 mm, 원주 30 mm 증가를 보였으며 서울에서 약 30 mm 감소하는 것으로 나타났다. 앞서 분석한 NSRPM매개변수의 거동에서 강우세포 수의 증가와 강우세포의 발생간격이 감소는 호우일수의 증가와 강우집중 시간동안의 강우량 증가의 결과로 나타나는 것으로 판단된다. 특히 강우세포수와 강우세포 발생간격에서 가장 큰 변화를 보인 원주 지점은 70개의 강우세포 수의 증가와 5시간 강우세포 발생간격이 감소를 확인하였으며 생성강우 특성에서도 호우일수와 강우집중 시간동안의 강우량에서 가장 높은 증가폭을 보였다. 그러나 1000년간의 강우를 생성하고 평균값을 취함으로서 강우량과 호우량은 관측 값보다 작게 나타나는 것으로 판단된다.

Fig. 3

Properties of observed rainfall in summer.

Fig. 4

Properties of generated rainfall in summer.