Article information

Abstract

Trans Abstract

1. 서 론

면적강우량은 유역단위의 수문 분석시 필수적인 요소이다. 면적강우량은 유역내 발생된 강우분포의 평균값을 의미한다. 기상 자료는 하나의 관측소가 수십~수백 km 반경을 대표하도록 구축된 기상 관측망을 통해 취득된다. 불규칙적으로 분포된 관측망을 통한 유역내 대표 강우량은 유역에 대한 평균강우량인 면적강우량을 계산하여 이용되고 있다. 면적강우량은 Arithmetic average, Thiessen polygon과 같은 가중치를 이용하는 방법과 kriging 등의 interpolation 방법을 통해 계산된다. 이러한, 면적강우량은 실제 유역내 강우 분포 계측이 불가능하다는 한계로 인해 불가역적으로 이용되어왔다. 정확한 면적강우량 산출이 선행되어야 연계된 수문량의 신뢰성이 확보될 수 있다(Rakhecha and Singh, 2009; Teegavarapu, 2022). 이러한 점에서, 면적강우량의 신뢰성을 확보하기 위해 다양한 연구가 수행되었다. 일반적으로 산정된 면적강우량 사이의 편의량 분석을 통해 면적강우량의 평가가 수행된다(Kruizinga and Yperlaan, 1978; Daly et al., 1994; Hijmans et al., 2005; Taesombat and Sriwongsitanon, 2009; Li and Shao, 2010; Wagner et al., 2012; Sene, 2015; Xu et al., 2015; Yang et al., 2015; Zhang et al., 2016; Chen et al., 2017; Liu et al., 2022). 이처럼, 다양한 기법을 통해 산정된 면적강우량은 임의의 관측소를 미계측 지점으로 가정하여 검정을 수행하고 오차 수준에 따라 방법의 적합성을 판단한다. 이러한 방법들은 취득 가능한 기상 관측망의 관측값에 한정하여 검정이 수행되므로 미계측 지역에 대한 직접적인 검정이 불가능다는 한계가 존재한다. 또한, 관측소의 영향 범위에서의 기상 패턴이 균등하다는 가정이 적용되는 이러한 방법들은 실제 발생되는 공간적 분포를 고려하지 못하며, 이러한 문제는 관측소의 영향범위가 클수록 심화된다(Gampe and Ludwig, 2017; Bližňák et al., 2022).

관측기술 발달로 레이더와 인공위성을 통해 공간적으로 연속된 강우자료가 취득됨에 따라 레이더 자료와 같은 연속된 강우 자료를 활용한 수문량 분석 연구가 활발히 수행되고 있다. 레이더 자료는 지상에 설치된 기상관측망 강우자료 대비 짧은 시간간격과 조밀한 공간해상도를 제공하므로 유역의 평균 강우량을 산정하는데 매우 적합하다. 레이더를 통한 강우 자료는 레이더로 취득된 반사도 자료를 변환하여 생성되는데, 이러한 과정속에서 레이더 강우량에 오차를 발생시키는 2가지 요인이 작용한다. 첫째로, 레이더 반사 감쇠, 지상, 지형 및 건물에 의한 이상 전파 및 차단 등에 따른 레이도 반사도의 부정확한 측정이 원인이다(Seo et al., 2015; McRoberts and Nielsen-Gammon, 2017). 두번째는, 측정된 레이더 반사도를 변환한 강우량의 오차문제로 이는 반사도의 수직단면의 변동성이 원인이다(Berne and Krajewski, 2013; Hall et al., 2015). 이와 같은 문제를 해소하기 위하여 지형간섭과 빔차폐의 영향을 최소화하여 정확도를 향상시키고자 하이브리드 스캔 반사도 강수추정기법에 관한 많은 연구들이 이루어졌다(Fulton et al., 1998; Zhang et al., 2011). 이러한 문제를 해결하기 위하여, 대한민국 기상청에서는 이중편파 레이더를 통한 3차원 자료수집을 기반으로 다중 고도각 기반 강우 추정을 적용한 다중 레이더 합성자료(Hybrid surface rainfall, HSR)를 개발 제공하고 있다(Fulton et al., 1998; Zhang et al., 2011).

기상 관측망을 통한 면적강우량 재현의 한계성을 인식하고, 레이더와 인공위성으로 취득된 연속적인 강우자료를 활용하여 유역의 면적강우량에 대한 대표성을 판단하는 연구들이 수행되었다. 실제 유역에서 발생되는 강우 패턴의 불규칙적인 변동성을 고려하는 측면에서 연속 강우 자료의 특성 반영의 중요성을 나타냈다(Haberlandt, 2007; Schiemann et al., 2011; Verworn and Haberlandt, 2011; Valles et al., 2020; Akgül and Aksu, 2021; Ahmed et al., 2022; Bližňák et al., 2022; Malede et al., 2022).

또한, 기상 관측망의 설치 밀도에 따른 수문 모형의 성능을 평가한 연구들에서는 관측 밀도가 조밀 할수록 수문량의 신뢰성이 증가함을 보여줬다(Lebel et al., 1987; Wood et al., 2000; Cheng et al., 2012).

이처럼, 다양한 연구에서 면적강우량의 중요성을 인식하고 적절한 면적강우량을 도출하기 위한 방법들이 개발 및 연구되고 있다. 하지만, 기상 관측망에 기반한 다양한 면적강우량 산정 방법들은 여전히 미계측 지역에 대한 직접적인 비교가 불가능하다는 명확한 한계가 존재한다. 또한, 여러 연구를 통해 조밀한 기상 관측망 구축이 신뢰성 있는 수문자료를 취득할 수 있음을 보여줬지만, 일부 유역에 한정된 사례 연구의 결과로서 분석 대상이 아닌 지역에 일반적으로 적용하기엔 어려움이 있었다.

이에 본 연구에서는 레이더 자료를 활용하여 기상 관측망 기반의 면적강우량의 신뢰성을 평가하였다. 기존 면적강우량과 실제 유역에서 발생되는 강우량 사이의 관계를 통해 기존 면적강우량의 적합성을 평가해보고자 한다. 본 연구에서는 면적강우량 방법을 적용하는 과정에서 발생하는 오차의 원인 규명과 유역의 대표 강우량을 도출하기 위한 기상 관측망의 설치 밀도에 대한 분석을 통해 수문분석에 적절한 면적강우량 선정 방안에 대해 살펴보았다.

2. 분석 방법 및 자료

2.1 대상지역 및 대상자료

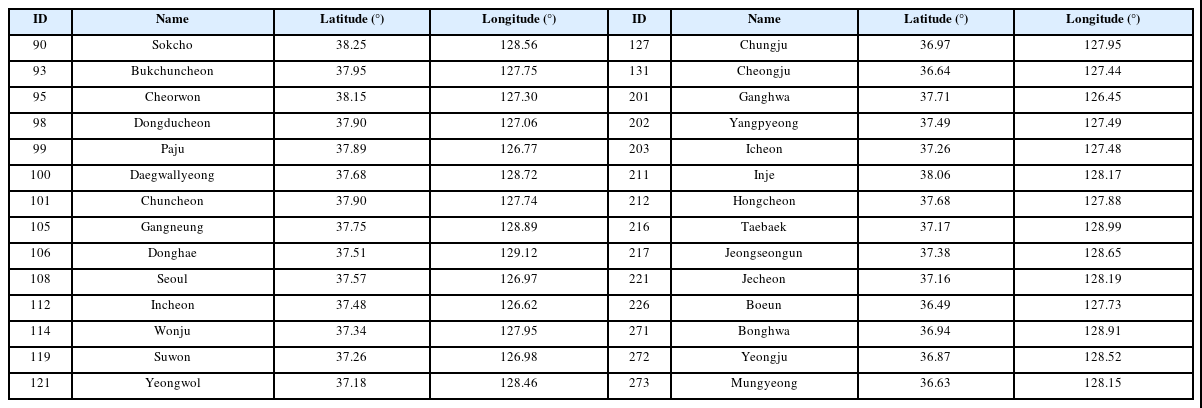
한국 기상청에서는 270종의 기상기후데이터를 기상자료개방포털을 통해 제공하고 있다. (2020, 기상기후데이터 카탈로그) 대한민국 전역의 강수 분포를 살펴볼 수 있는 기상관측자료는 96지점의 종관기상관측소(Automated Synoptic Observing System, ASOS), 504지점의 방재기상관측소(Automatic Weather System, AWS), 10지점의 레이더 자료를 합성한 HSR 레이더 합성영상자료(Hybrid Surface Rainfall, HSR)가 취득/운영되고 있다. 방재기상관측소는 2000년 이후로 설치 운영되고 있으므로 장기간 강수자료를 생성하는데 어려움이 존재한다. 본 연구에서는 Fig. 1과 Table 1에서와 같이 제공되는 2종의 기상관측자료에 대하여 2021. 1. 1. 01:00~2021. 12. 31. 24:00 기간 동안의 자료를 취득하고, 공통적으로 적용 가능한 최소 시간 간격인 1시간 간격으로 변환하여 이용했다.

Fig. 1

Map of Study Area and Installed Precipitation Observatory

Table 1

Type of Precipitation Observation Instrument

수자원단위지도는 국가 차원의 수자원개발, 계획 및 관리업무의 효율적 추진을 위하여 수자원 업무에 활용되는 자료의 수집, 분석과 물관련 기관 간 자료의 공동활용을 목적으로 지형공간 상에 대권역, 중권역 및 표준유역의 가상의 구역을 설정한 지도이다. 일반적으로 대상 유역에 대한 수문량 분석은 대상 유역별로 수행되며, 대상 유역에서 발생된 강우량을 나타내는 유역강우량 산정이 우선적으로 이루어진다. 대한민국의 수자원단위지도는 환경부에서 관리 배포되며, 국토교통부에서 운영되는 국가공간정보포털(National Spatial Data Infrastruckture Portarl)에서 무료로 배포되고 있다. 본 연구에서는 한강유역을 구분한 대권역 1개와, 24개 중권역 및 237개 표준유역의 수자원단위지도를 사용했다.

2.2 연구방법

지상에 설치된 기상 관측 장비를 통해 취득된 기상 관측자료는 기상 관측망의 구축 밀도에 따라 설치 위치를 중심으로 반경 수십~수백 km를 대표한다. 반면, 관측기술의 발달에 따라 유역 전체에 분포하는 강우량을 연속적으로 취득 가능한 레이더 강우 자료는 500 m 간격의 연속된 강우량 자료를 제공하고 있다. 일반적으로 유역내 수문 분석에 적용되는 면적강우량은 불연속적으로 분포된 강우자료를 이용한 유역의 평균 강우량을 산정할 수 있도록 Thiessen weighted rainfall (TW) 방법이 개발되어 사용되었다. 또한, 장기간 강수자료를 보유하고 있는 종관기상관측망(ASOS) 자료를 기반으로 면적강우량이 산출되어 이용되어지고 있다.

레이더를 통해 취득된 강우자료는 유역 전체에 분포된 연속된 자료임으로 유역에 위치한 레이더 자료의 평균을 통해 유역의 면적강우량이 산출된다. 레이더를 통해 산출된 면적강우량은 공간적 불연속 한계를 해결함으로써 기존 방법에 비해 유역 단위를 대표하는 면적강우량을 산정할 수 있다. 하지만, 레이더 강우자료와 지상 관측 장비를 통한 강우 자료 사이의 양적 편차 문제는 레이더 강우자료의 활용을 저해하는 요소로 작용되고 있다.

본 연구에서는 레이더 강우자료와 지상 강우 자료 사이의 양적 편의 문제와 무관하게 공간적 연속성 고려 여부에 따른 면적강우량의 변동성과 기존에 사용되어지고 있는 면적강우량이 유역에 대한 대표성을 나태내줄 수 있는지에 대하여 평가하였다. 기존에 사용된 지점관측망을 활용한 TW 방법의 면적강우량이 면적강우량으로 정의된 유역의 평균 강우량을 효과적으로 나타내주고 있는지를 한강유역에 대하여 분석하였다.

이러한 연구를 진행하기 위하여 총 3단계의 연구과정을 수립하였다. 1단계는, 전통적으로 사용되는 면적강우량을 계산하기 위해 한강유역에 인접한 28개 ASOS 관측소를 포함하는 레이더 격자를 추출하여 TW 방법을 통한 면적강우량을 계산한다. TW 방법에 이용된 ASOS 관측소의 위치 정보와 적용 결과는 Table 2와 Fig. 2와 같다. 2단계는 유역내 위치한 레이더 격자의 평균강우량을 계산하여 실제 면적강우량으로 정의한다. 1, 2단계는 한강유역의 대권역, 중권역, 소권역에 각각 적용되며, 티센망을 통해 구분된 각각의 티센 다각형에 대하여도 면적강우량을 산정한다. 3단계 과정은 1, 2단계에서 구축된 면적강우량의 비교 분석을 통해 기상 관측망과 유역 면적 변화에 따른 면적강우량 사이의 관계성을 분석하고 전통적 방법을 통한 면적강우량의 유역 대표성에 대해 평가하였다.

Table 2

Location of the Weather Stations in Han-river Basin

Fig. 2

Map of Hydrologic Units Over Han River Basin and Thiessen Polygon by Asos Network

본 연구에서 기상 관측망과 레이더 자료에 대한 면적강우량을 생성하기 위해 각각 Thiessen weighted rainfall 방법과 유역의 평균을 산출하는 방법을 적용하였다. 각각의 방법은 다음식과 같다. 전통적인 티센 면적강우량인 Eq. (1)과 레이더를 통한 면적강우량인 Eq. (2)는 차이점은 강우의 발생 분포의 고려 여부이다. 티센 면적강우량은 항상 동일한 면적 가중치를 반영하는 반면, 레이더 면적강우량은 강우의 분포에 따라 가중치가 변동한다.

Type1 : Areal rainfall by thiessen weighted rainfall

(1)Parea=∑i=1n(Pi×Areai)Areawatershed

여기서, Area는 면적을 i는 티센 다각형을 n은 대상 유역에 대한 티센 다각형의 총 수를 나타낸다.

Type2 : Areal rainfall by mean radar ranfall

(2)P′area=∑i=1n(Pi×Drained Areai)Areawatershed       =∑i=1n∑j=1m(Pj×Areaj)Areawatershed

여기서, Area는 면적을 i는 티센 다각형을 n은 대상 유역에 대한 티센 다각형의 총 수를 나타낸다. j는 i번째 티센 다각형내 위치한 레이더 격자를 나타내며 m은 i번째 티센 다각형에 위치한 레이더 격자의 총 수를 나타낸다.

3. 결과 및 논의

본 절에서는 ASOS 강우관측망 위치에 있는 28개 레이더 격자 강우량을 활용하여 기존에 활용되어온 티센망을 통한 면적강우량과 유역내 모든 레이더 격자자료를 평균하여 도출한 레이더 면적강우량을 산정하였다. 레이더 면적강우량은 면적강우량의 정의에 부합하므로 실제 면적강우량으로 가정하고 티센망을 통한 면적강우량과 비교 분석을 수행했다.

Fig. 3은 한강 대권역에 대하여 구축된 티센망 중 철원관측소(No.95)와 봉화관측소(No.271)가 차지하는 면적에 대하여 두가지 방법을 이용한 면적강우량 산정시 산출되는 가중치를 도시한 결과이다. 철원과 봉화 관측소는 가장 크고, 가장 적은 티센 면적을 갖는 지점들로 티센 면적 비중에 따른 강우의 분포 특성을 비교하고자 대표 관측소로 선정됐다. 티센망에 기반한 가중치는 전체 한강유역에 대한 철원관측소에 할당된 면적비로 항상 0.2373의 가중치가 반영되는 반면, 레이더 면적강수량의 경우 철원관측소에 할당된 면적 중 강우가 분포한 면적에 대한 가중치가 산정되므로 강우의 발생 분포에 따라 변동하며, 모든 면적에 강우가 분포할 경우만 티센망 기반 가중치와 동일한 가중치가 나타났다. 또한, 레이더 면적강수량 가중치에 대한 상대도수를 보여주는 오른쪽 막대그래프에서는 철원관측소 지역의 경우 적은 가중치에 치우친 결과가 나타났다. 반면 봉화관측소(No.271)의 경우 티센망 가중치에 인접한 가중치에 치우친 가중치 분포가 나타났다. 두 지역의 차이점은 각각의 관측소가 대표하는 티센망의 면적이라 볼 수 있으며, 면적이 클수록 지역 전체에 강우가 분포되지 않음으로서 티센 가중치와의 차이가 크게 나타났다.

Fig. 3

Weight Factor Sequences from 01:00 on January 1st, 2021, to 24:00 on December 31st, 2021 for Thiessen Polygon Areas in the Han River Basin (Top - No.95 Station, Bottom - No.271 Station)

이러한 특성을 파악하기 위해 2021년 시간별 강우자료를 이용하여 대권역, 중권역, 표준유역에 대하여 구축된 558개 티센망에 대하여 모든 시 강우량에 따른 티센 면적별 [레이더 가중치/티센 가중치] 비를 산정했다. Fig. 4는 558개 티센 면적에 따른 [레이더 가중치/티센 가중치] 비의 평균값을 도시한 결과로 면적과 가중치 비율 간에 0.94의 R-square를 갖는 모형이 구축되어 높은 관계성이 나타났다. 레이더 가중치와 티센 가중치의 비가 100%를 나타낼 경우 해당 면적에서 강우가 발생할 경우, 면적 전체에 강우가 분포함을 나타낸다. 가중치의 비가 50%를 나타낼 경우, 해당 면적에서 강우가 발생할 경우 레이더 강우의 경우 전체 면적 중 50%의 면적에서만 강우가 발생함을 의미한다. 만약, 두 면적강우량에 대한 가중치 비가 항상 100%을 나타내는 지역이 있다면, 실제 지역내 강우분포와 티센 가중치가 동일하므로 연관된 지점 관측소가 강우의 분포 측면에서 해당 지역을 대표 할 수 있다고 볼 수 있다. Fig. 4에서 90% 이상의 비를 갖는 면적은 10 km² 이하부터 나타나며, 1 km² 이하의 면적을 갖는 지역에서 99% 이상의 가중치 비가 나타났다. 이러한 결과는, 지점 관측소가 임의 지역에 발생하는 강우 분포를 대표하기 위해서는 1 km² 이하의 관측망 밀도를 필요로 한다고 볼 수 있다. 또한, 면적이 2,000 km² 이상인 지역의 경우 50% 이하의 비가 나타났다. 50% 비는 만약 레이더 면적강우량과 지점 관측소가 동일한 강우량을 갖을 경우, 티센 면적강우량이 실제 면적강우량보다 2배 큰 결과를 갖는 것을 의미한다.

Fig. 4

Contributing Mean Ratio [Radar Weight/Thiessen Weight] on the Thiessen Polygon Area for All Basin Over Han River Basin in 2021 and All Rainfall Time Series

실제 유역내 면적강수량과 티센 방법을 통한 면적강수량을 비교하기 위하여 면적강수량의 비를 [레이더 면적강수량/티센 면적강수량]으로 나타냈다. 면적강수량의 비는 한강 유역의 262개 수자원단위지도(1개 대권역, 24개 중권역, 237개 표준유역)와 2021년 1시간 강우자료를 이용하여 강우가 발생한 모든 경우에 대한 결과를 산정했다. Fig. 5에서와 같이 1시간 면적강우량이 25 mm 이상일 경우 평균 면적강우량의 비가 0.25이며 95% 신뢰구간이 (0.3 0.56)으로 1보다 적은 강우비가 분포하므로 티센 면적강우량이 실제 면적강우량 보다 크게 산정되었음을 볼 수 있다. 티센 면적강우량이 5 mm 이하의 경우 대체로 평균 면적강우량비가 1.17로 1보다 큰 면적강우량 비가 분포되어 있으므로 실제 유역의 면적강우량에 비해 과소 산정됨을 볼 수 있다. 일반적으로 티센 면적강우량이 적을 경우 과소 추정되며, 티센 면적강우량이 커질수록 과대 추정되어 지는 현상이 나타났다. 티센면적강우량 구간에 따른 평균 면적강우량비와 95% 신뢰구간은 Table 3과 같다.

Fig. 5

Contributing Areal Rainfall Ratio [Radar/Thiessen] on All Basin Over Han River Basin in 2021 and All Rainfall Time Series

Table 3

Statistics on Areal Rainfall Ratio according to Thiessen Weighted Rainfall Range (The 95% Confidence Interval is in Parentheses)

지점 강우 관측망을 이용한 면적강우량 산정시 지역내 강우분포 변동성을 고려하지 못하는 문제와 지역에 대한 대표 강우량을 확보하기 어려운 관측망의 설치 밀도로 인하여 실제 면적강우량과 오차가 발생했다. 대표적인 오차의 유형으로는 유역내 강우 분포가 존재하지만 기상 관측망에서 강우가 발생되 않았을 경우, 티센 면적강우량은 0으로 산정될 수 있는데 이 경우, 강우의 발생 패턴이 달라지는 문제가 발생한다. 또한, 유역에서 기상 관측망 주변 일부만 강우 분포가 존재하고 나머지 지역은 강우가 발생하지 않았을 티센 면적강우량은 실제 면적강우량에 비해 과대 산정될 수 있다. 넓은 면적에 영향을 미치는 극치 강우가 발생할 경우, 지점 관측망이 영향을 미치는 면적이 커질수록 지점 관측망의 대표성이 감소하여 실제 면적강우량보다 크게 산정된다. 임의의 지역 단위에 발생되는 강우는 강우의 분포와 양적 변동성이 존재하므로 항상 동일한 가중치를 적용하여 추정되는 지점 관측망 기반 면적강우량은 필연적으로 실제 면적강우량 대비 추정 오차가 발생될 수 있다. 이러한 오차는 한강 유역의 지점 관측소의 영향 면적과 강우 분포비를 나타낸 Fig. 4와 한강 유역의 티센 가중 방법에 기반한 면적강우량과 실제 면적강우량비를 나타낸 Fig. 5에서 확인된다.

4. 결 론

본 연구에서는 강우 관측 기술의 발달로 인하여 격자 형태로 연속된 레이더 강우 자료 취득이 가능해짐에 따라 기존 수문 분야에서 사용되는 면적강우량의 적절성을 평가했다. 한강 유역에 위치한 다양한 면적의 유역들과 1시간 강우량의 강우 사상을 적용하여 공간적 연속성의 중요성을 인식시키고, 실제 면적강우량과의 비교를 통해 기존 면적강우량에 내포된 편차와 발생 원인을 규명했다.

레이더 자료를 이용한 한강 유역의 면적강우량 평가 결과 기존의 지점 관측망을 활용한 면적강우량은 실제 지역에서 발생되는 강우분포의 변동성을 반영하지 못하여 즉, 지점 강우 관측소가 해당 지역에 대한 대표성을 확보하지 못하는 문제를 확인하였다. 지점 관측망의 지역 대표성은 관측망의 밀도 증가를 통해 증진시킬 수 있지만, 대표성 확보를 위한 관측밀도는 1 km² 이하로 현실적으로 구축하기 힘든 관측밀도이다.

이러한 이유로, 유역 단위의 수문량 분석시 레이더와 같은 유역내 강우분포를 적용한 면적강우량과 지점 관측소 기반의 유역 평균 강우량 사이의 강우발생 패턴과 양적인 수문량 차이가 발생함을 확인하였다. 수문량 차이는 유역내 강우와 홍수 시계열 구축에 큰 영향을 미치므로 본 연구에서는 유역의 시계열 자료 구축시 공간적 연속성이 고려된 레이더 면적강우량의 활용 방안을 고려할 필요가 크다고 판단된다. 또한, 본 연구에서 나타낸 면적별 강우분포 발생비율은 지점 강우량의 대표성이 확보될 경우, 면적감소계소와 동일한 개념을 보여줌으로 한강 유역에 대한 면적감소계수 산정 방안의 하나로 이용될 수 있을 것으로 판단된다. 이러한 발생 비율은 호우중심 사상에 비해 유역의 특성을 보다 적절하게 반영할 수 있다는 장점이 있다.

지점 강우 관측망에 기반한 면적강우량을 이용할 경우, 본 연구의 결과가 면적강우량의 보정 방안을 마련하는데 도움이 될 수 있을 것으로 판단된다. 후속 연구로, 레이더 면적강우량 자료를 이용한 유출량 평가 연구와 레이더 면적강우량에 기반한 극치 강우량 계열의 면적감소계수 산정 방안에 대한 연구를 수행하고자 한다.

Article information Continued