1. 서 론
흙의 포화투수계수(Ksat (saturated hydraulic conductivity))는 댐과 같은 많은 지반 구조물의 안정성 평가에 매우 중요한 물성치이며 특히 강우 침투 산정이나 사면안정성 평가에 매우 중요하다. 흙의 포화투수계수는 흙의 종류 및 특성에 따라 매우 넓은 범위의 값을 보이며 큰 불확실성을 나타낸다. 따라서 정확한 흙의 포화투수계수 산정은 관심지역의 흙 시료 채취를 통한 정수위(constant head test)나 변수위(falling head test) 실내실험 또는 slug test와 같은 현장투수실험을 통하여 산정된다.
실내실험을 통한 포화투수계수의 평가는 실험시간이 상대적으로 짧고 적은 비용으로 수행이 가능하나 샘플의 크기의 영향에 크게 받는 포화투수계수의 특성 때문에 비균질한(heterogenous) 지반의 경우 정확한 평가가 어렵다. 또한 현장실험의 경우 현장의 흙을 교란하지 않고 넓은 지역에서의 포화투수계수를 평가할 수 있는 장점이 있으나 실험시간이 길고 비용이 많이 소요된다는 단점이 있다. 따라서 높은 정확도를 가진 흙의 포화투수계수 예측 모델 구축이 필요하다.
현재까지 많은 연구자들이 소성지수(plasticity index), 비표면적(specific surface), 입자크기, 간극률 등과 같은 흙의 물성치를 이용한 포화투수계수 예측모델을 제안하였다(
Dolinar, 2009;
Chapuis, 2012;
Ren and Santamarina, 2018;
Babaoglu and Simms, 2020). 이러한 예측모델은 제안된 식과 쉽게 측정가능한(easy-to-measure) 물성치를 이용하여 비교적 간단하게 포화투수계수 예측이 가능하다. 하지만 대부분의 모델은 점토에서부터 굵은 모래까지 모든 범위의 흙에 대한 적용이 가능하지 않거나 특정한 흙에 대하여 낮은 정확도를 보인다. 또한 투수계수에 영향을 미치는 수많은 영향인자(e.g., 간극률, 유기물 함량, 입도분포곡선, 입자모양, 간극수의 화학적 성질)들을 고려하지 못한다. 따라서 많은 영향인자를 고려할 수 있고 대부분의 흙에 적용가능한 포괄적인 예측모델이 필요하다.
최근에 대두되는 머신러닝(Machine Learning) 알고리즘을 이용한 예측모델은 포화투수계수과 같이 불확실성이 매우 큰 흙의 물성 예측에 많이 이용된다. 예를 들어 머신러닝 알고리즘 중 한 종류인 인공신경망(Artificial Neural Network, ANN)을 이용한 포화투수계수 예측모델은 높은 정확도를 보인다(
Parasuraman et al., 2006;
Agyare et al., 2007). 따라서 본 연구에서는
Pachepsky and Park (2015)이 제안한 USKSAT 포화투수계수 데이터베이스를 이용하여 인공신경망 기반 포화투수계수 예측모델을 제안하였다. ANN 모델의 최적화 알고리즘(optimization algorithm)과 노드(node)와 은닉층(hidden layer)의 개수를 통하여 최적의 성능(performance)를 보이는 모델을 제안하고 논의하였다. 또한 구축된 ANN 모델을 이용하여 흙의 종류별 포화투수계수 예측성능을 산정하고 논의하였다.
2. 학습 데이터베이스
2.1 USKSAT 데이터베이스
본 연구에서는 미국 지역의 흙에 대한 실내실험(정수위 또는 변수위 투수 실험)을 통하여 측정된 총 18,329개의 USKSAT 데이터베이스를 ANN 모델 구축에 이용하였다(
Pachepsky and Park, 2015). 데이터베이스의 포화투수계수(
Ksat)는 약 10
-3~10
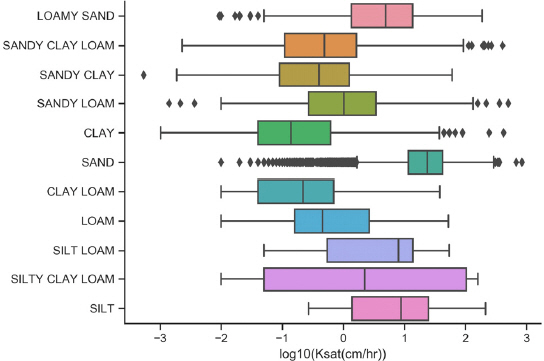
3 cm/hr의 분포를 보이며 USDA (U.S. Department of Agriculture)에 의해 분류된 11가지 흙의 포화투수계수를 포함한다. 흙의 종류별
Ksat의 분포는
Fig. 1에 나타내었다.
Fig. 1
Boxplots of Log10 (Ksat) for 11 Soil Textures Used in Development of ANN-Based Prediction Model
본 연구에서는 데이터베이스에 존재하는 예측변수 중 포화투수계수에 영향을 미칠 수 있는 13가지 예측변수를 선택하여 ANN 기반 예측모델 구축의 입력변수로 이용하였다. 입력변수로 이용한 13가지 예측변수와 각각의 예측변수에 대한 통계값은
Tables 1과
2에 나타내었다.
Table 1에 나타난 바와 같이 데이터베이스의 예측변수는 흙의 상태에 따른 예측 변수 1개(ρ
b), 입경에 따른 흙의 구분 관련 예측변수 8개(
Fsand,
Fsilt,
Fclay, VCOS, COS, MS, FS, VFS), 흙 입자의 입도분포곡선 관련 예측변수 3개(
d10,
d50,
Cu), 기타 흙의 성질 관련 예측변수 1개(OC)로 구성되었다. 또한 대부분의 데이터는
Fsand > 50%로 정의되는 조립토(17,107개)로 나타났고 이는 매우 큰
Fsand의 중간 값(92% in
Table 2)으로 나타났다.
Table 1
Notations of 13 Selected Predictors and Corresponding Descriptions
|
Notation |
Description |
|
ρb (g/cm3) |
Bulk density |
|
OC
|
Organic content |
|
Fsand (%) |
Sand content |
|
Fsilt (%) |
Silt content |
|
Fclay (%) |
Clay content |
|
VCOS (%) |
Very coarse sand fraction |
|
COS (%) |
Coarse sand fraction |
|
MS (%) |
Medium sand fraction |
|
FS (%) |
Fine sand fraction |
|
VFS (%) |
Very fine sand fraction |
|
d10 (%) |
10th percentile particle size |
|
d50 (%) |
Median particle size |
|
Cu
|
Coefficient of uniformity |
Table 2
Statistical Descriptions of 13 Predictors in the Database
|
Predictor |
Mean ± Sth. |
Median |
CV |
|
ρb (g/cm3) |
1.53 ± 0.17 |
1.55 |
0.11 |
|
log10 (OC) |
-0.60 ± 0.57 |
-0.66 |
-0.95 |
|
Fsand (%) |
85.67 ± 15.84 |
92.00 |
0.18 |
|
Fsilt (%) |
5.57 ± 7.08 |
3.80 |
1.27 |
|
Fclay (%) |
8.77 ± 11.89 |
3.10 |
1.36 |
|
VCOS (%) |
0.34 ± 1.05 |
0 |
3.09 |
|
COS (%) |
3.76 ± 4.54 |
2.1 |
1.21 |
|
MS (%) |
20.89 ± 16.79 |
16.8 |
0.8 |
|
FS (%) |
50.22 ± 20.57 |
49.4 |
0.41 |
|
VFS (%) |
10.45 ± 8.58 |
8.2 |
0.82 |
|
d10 (%) |
51.95 ± 44.46 |
55.92 |
0.86 |
|
d50 (%) |
167.15 ± 68.75 |
156.30 |
0.41 |
|
log10 (Cu) |
2.84 ± 2.62 |
1.19 |
0.92 |
2.2 다중공선성(multicollinearity)을 이용한 예측변수 set의 선정
본 연구에서 이용한 데이터베이스와 같이 예측변수의 수가 많을 경우 일반적으로 예측 모델 구축 전 예측변수간의 상관관계를 이용하여 독립적인 예측변수들을 예측모델의 예측변수로 선정하게 된다. 다른 예측변수와 강한 상관관계(일반적으로 Pearson’s coefficient를 통하여 산정)를 보이는 예측변수는 모델의 정확도를 향상시키지 못하고 모델의 복잡성(complexity) 증가 및 사용성 감소를 야기하므로 모델구축 시 제외된다. 하지만 이러한 하나의 변수들 간의 상관관계는 예측 값과 물리적으로(또는 이론적으로) 강한 상관관계를 보이는 예측변수를 예측모델에서 제외시킬 위험이 존재한다. 예를들어 기존의 수많은 선행연구들로 상관관계가 증명된 점토함량(Fclay)나 d10이 Ksat 예측모델에서 제외될 가능성이 존재하고 이러한 예측변수를 제외하고 구축된 예측모델은 물리적 현상에 기반하지 않은 단순한 수학적 예측모델이 된다. 따라서 본 연구에서는 VIF (Variation Influence Factor)를 산정하여 각 변수들의 다중공선성(multicollinearity)를 판단하였다.
다중공선성은 여러 가지 예측변수의 공존에 의한 예측모델의 왜곡을 방지하기 위하여 산정되며 다중공선성이 높은 예측변수는 일반적으로 제거된다. 예측변수의 다중공선성은 VIF > 10일 때 높다고 판단하며 VIF는 예측변수와 다른 예측변수들간의 다중선형회귀분석(multilinear regression)을 통하여 이루어진다. i번째 예측변수에 대한 VIF는 Eq. (1)을 통하여 산정된다.
여기서 Ri2은 i번째 예측변수와 나머지 예측변수들간의 다중선형회귀분석 결정계수이다.
Table 3은 데이터베이스의 13가지 예측변수들에 대한 VIF값을 나타낸다.
Table 3에 나타난 바와 같이 ρ
b OC,
d10,
Cu를 제외한 나머지 모든 변수들이 VIF > 10로 강한 다중공선성을 보였다. 하지만
d50이나
Fclay와 같은 변수는 물리적으로
Ksat에 큰 영향을 미치며 물리 기반 예측모델 구축을 위하여 예측변수에 포함되어야 한다. 따라서 본 연구에서는 VIF > 10의 기준을 적용하여 다중공선성이 큰 변수들을 제외한 네 가지 예측변수 set을 통한 ANN 기반 예측모델과
Table 3의 모든 예측변수를 적용한 예측모델을 개발하고 두 가지 모델의 예측성능을 비교 및 논의하였다.
Table 3
Variation Inflation Factor (VIF) Values of 13 Predictors
|
Predictor |
VIF |
|
ρb (g/cm3) |
1.67 |
|
log10 (OC) |
1.59 |
|
Fsand (%) |
2.01 × 108
|
|
Fsilt (%) |
1,495.9 |
|
Fclay (%) |
4,626.5 |
|
VCOS (%) |
8.99 × 105
|
|
COS (%) |
1.67 × 107
|
|
MS (%) |
2.28 × 108
|
|
FS (%) |
3.41 × 108
|
|
VFS (%) |
5.89 × 107
|
|
d10 (%) |
6.72 |
|
d50 (%) |
18.32 |
|
log10 (Cu) |
7.91 |
3. ANN 예측모델 개발
3.1 인공신경망(Artificial Neural Network) 모델
여러 가지 머신러닝 모델 중 ANN 모델은 모델 구축과 하이퍼파라미터 튜닝이 비교적 간단하다는 장점이 있다. 따라서 크랙 탐지(crack detection)이나 말뚝의 표면마찰(skin friction) 예측, 지반진동 파라미터 예측 등에 이용되었다(
Goh, 1994,
1995;
Alavi and Gandomi, 2011;
Cha et al., 2017). ANN 모델은 입력층(input layer), 은닉층(hidden layer), 그리고 출력층(output layer)로 구성되어 있고 각각의 layer는 여러 개의 노드(node)로 구성되어 있다. 이전 layer의 i번째 노드값(
xi)와 다음 layer의 j번째 노드값(
xj) 사이의 가중치 함수(weight function)는 Eq. (2)를 통하여 산정된다.
여기서 f는 활성화함수, wij는 xi와 xj 사이의 가중치 계수(weight coefficient), b는 bias값이다.
본 연구에서는 노드값의 비선형성을 반영하고 0에서 1사이의 값을 가지는 sigmoid 활성화 함수를 이용하였고 training 함수는 베이지안 정규화 backpropagation 함수를 이용하였다. 또한 65, 15, 20%의 비율로 데이터는 나누어 각각 training, validation, test (각각 11,914개, 2,749개, 3,666개의 데이터)에 이용하였다. 모델의 성능은 평균 제곱 오차(Mean squared error)로 측정하였고 구해진 가중치의 gradient가 1 × 10
-7 이하이거나 Marquardt adjustment parameter가 1 × 10
10보다 크거나 iteration이 4,000번 이상 수행되면 training을 멈추는 stop criteria를 적용하였다. 본 연구의 ANN 예측모델구축에는 MATLAB이 이용되었고 흙의 종류에 따른 투수계수 매우 큰 변동성을 고려하기 위해 측정된
Ksat의 로그 값(log (
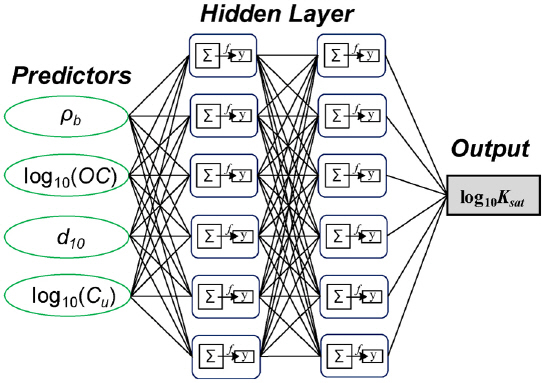
Ksat))을 모델 구축에 이용하였다. VIF > 10의 예측변수를 제거한 ANN 예측모델의 구조는
Fig. 2와 같다.
Fig. 2
Structure of the ANN Model for 4 Predictors and 2 Layers with 6 Nodes Each
3.2 최적의 모델 구축을 위한 모델링 시나리오
주어진 데이터베이스에 대한 ANN 모델의 성능은 layer수나 node수에 따라 달라지게 된다. 최적의 성능을 도출하는 layer수나 node수는 데이터베이스에 따라 상이하며 따라서 본 연구에서는 최적의 ANN 예측 모델 구축을 위하여 1, 2, 3개의 layer수과 각각 layer의 노드 수에 따른 총 10가지의 시나리오에 따른 ANN 모델을 구축하고 성능을 비교하였다. 본 연구에서 구축된 ANN 모델의 모든 시나리오에 대한 layer와 node수는
Table 4와 같다.
Table 4
Variation Inflation Factor (VIF) Values of 13 Predictors
|
Scenario No. |
Number of layers |
Number of neurons |
|
1 |
1 |
6 |
|
2 |
1 |
18 |
|
3 |
1 |
36 |
|
4 |
1 |
54 |
|
5 |
2 |
[6 6] |
|
6 |
2 |
[12 12] |
|
7 |
2 |
[18 18] |
|
8 |
2 |
[24 24] |
|
9 |
3 |
[12 12 6] |
|
10 |
3 |
[18 18 12] |
4. 결과 및 토의
4.1 ANN 모델구축 결과
본 연구에서는 예측된 Ksat의 변동성이 측정된 Ksat을 통해 예측가능한 정도를 나타내는 결정계수(R2)값과 측정된 Ksat와 예측된 Ksat의 평균 오차를 나타내주는 Root mean squared error (RMSE)를 통하여 모델의 성능을 평가하였다.
Figs. 3과
4는 각각 데이터베이스의 training set과 test set에 대한 ANN 모델을 개발한 결과를 나타낸다.
Figs. 3과
4의 결과는
Table 4의 Scenario No. 4에 해당하고 traning set과 test set에 대한 R
2값이 각각 0.899와 0.876으로 높은 성능을 보였다.
Figs. 3과
4 사이의 유사한 R
2값과 RMSE값은 개발된 모델에 과적합 문제가 나타나지 않았음을 뜻한다.
Fig. 3
Performance of Developed ANN Model for Training Set (Single Layer with 54 Neurons)
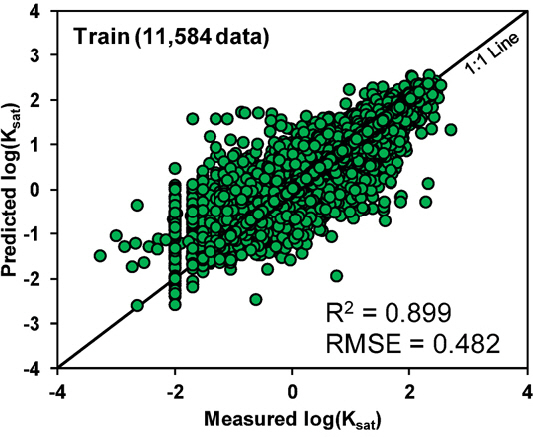
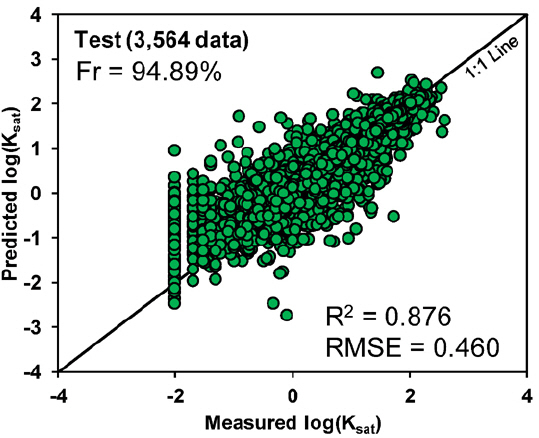
Fig. 4
Performance of Developed ANN Model for Testing Set (Single Layer with 54 Neurons)
Tables 5와
6은 각각 VIF > 10에 의한 4가지 예측변수(ρ
b OC,
d10,
Cu,
Table 3)와
Table 3의 모든 예측변수를 적용하여
Table 4에 나타낸 모든 시나리오에 대한 ANN 모델을 구축한 결과이다. 모델의 정확도 평가를 위하여 R
2과 RMSE는 일반적으로 모델의 정확도를 평가하기 위해 산정하는 지표들이지만 1:1 Line에서 상대적으로 멀리 떨어진 소수의 데이터에 크게 영향을 받기 때문에 합리적인 범위안의
Ksat 예측 확률에 대한 평가가 불가능하다. 따라서 본 연구에서는 측정된
Ksat의 0.1과 10배 사이(Measured
Ksat × 10
-1 < predicted
Ksat < Measured
Ksat × 10)의 예측 성능을 보이는 데이터의 수를 전체 데이터 수로 나눈 Fr 값을 산정하여 예측 성능을 평가하였다. Fr 값은 높은 불확실성을 보이는 지반의
Ksat 특성을 반영한 신뢰도 높은 예측 성능을 나타낸다. 데이터베이스의 Training, validation, test은 임의로 나누어졌기 때문에 산정된 모델 성능의 반복성을 나타내기 위하여
Tables 5와
6의 R
2, RMSE, 그리고 Fr 값은 10번 산정에 대한 평균값 ± 표준편차로 나타내었다.
Table 5
R2, RMSE, and Fr Values of Developed ANN Models (4 Predictors)
|
Scenario No. |
R2
|
RMSE |
Fr |
|
1 |
0.8365 ± 0.0037 |
0.5133 ± 0.0061 |
0.9309 ± 0.0032 |
|
2 |
0.8341 ± 0.0123 |
0.5165 ± 0.019 |
0.9305 ± 0.0041 |
|
3 |
0.8299 ± 0.0111 |
0.5234 ± 0.0186 |
0.9325 ± 0.0035 |
|
4 |
0.8212 ± 0.0312 |
0.5397 ± 0.0530 |
0.9317 ± 0.0041 |
|
5 |
0.8339 ± 0.0176 |
0.5197 ± 0.0248 |
0.9306 ± 0.0030 |
|
6 |
0.8047 ± 0.0416 |
0.5652 ± 0.0623 |
0.9301 ± 0.0049 |
|
7 |
0.8227 ± 0.0149 |
0.5368 ± 0.0248 |
0.9314 ± 0.0049 |
|
8 |
0.7668 ± 0.0587 |
0.6446 ± 0.1118 |
0.9262 ± 0.0047 |
|
9 |
0.8125 ± 0.0201 |
0.5530 ± 0.0325 |
0.9297 ± 0.0021 |
|
10 |
0.7869 ± 0.0395 |
0.6003 ± 0.0666 |
0.9256 ± 0.0069 |
Table 6
R2, RMSE, and Fr Values of Developed ANN Models (All Predictors in Table 3)
|
Scenario No. |
R2
|
RMSE |
Fr |
|
1 |
0.8473 ± 0.0039 |
0.4995 ± 0.006 |
0.9361 ± 0.0024 |
|
2 |
0.8542 ± 0.0063 |
0.4864 ± 0.0098 |
0.9400 ± 0.0036 |
|
3 |
0.8567 ± 0.0070 |
0.4845 ± 0.0123 |
0.9413 ± 0.0041 |
|
4 |
0.8438 ± 0.0180 |
0.5117 ± 0.0285 |
0.9405 ± 0.0054 |
|
5 |
0.8507 ± 0.0047 |
0.4946 ± 0.0071 |
0.9372 ± 0.0043 |
|
6 |
0.8532 ± 0.0088 |
0.4932 ± 0.0153 |
0.9394 ± 0.0034 |
|
7 |
0.8542 ± 0.0081 |
0.4948 ± 0.0136 |
0.9436 ± 0.0043 |
|
8 |
0.8371 ± 0.0201 |
0.5306 ± 0.0392 |
0.9429 ± 0.0037 |
|
9 |
0.8487 ± 0.0182 |
0.5003 ± 0.0322 |
0.9409 ± 0.0037 |
|
10 |
0.8426 ± 0.0093 |
0.5194 ± 0.0142 |
0.9413 ± 0.0031 |
Tables 5와
6에 나타난 바와 같이
Table 3의 모든 예측변수를 모델구축에 이용한 경우 더 높은 성능의 ANN 모델이 구축되었다. 달리 말하면, 같은 은닉층 수와 노드 수 설정 시
Table 6에서 더 높은 R
2, RMSE, 그리고 Fr값이 나타났다. 또한 같은 시나리오에서
Table 6이 더 높은 표준편차를 보였고 모델의 성능이 전체적으로 은닉층 수와 노드 수의 변화에 덜 민감하였다(0.7668 < R
2 < 0.8365 (
Table 5), 0.8371 < R
2 < 0.8567 (
Table 6)). 이는 다중공선성을 가지는 예측변수 제거가 모델의 성능이나 반복성에 부정적인 영향을 끼침을 보여준다. 하지만 상대적으로 높은 정확도를 보이는
Table 5의 시나리오는 예측모델의 사용성 증가 및 효과적인 모델 구축을 위한 예측변수 제거 시에 VIF > 10에 의한 예측변수 제거가 가능하다는 것을 보여준다. 특히 다른 시나리오들에 비해 상대적으로 높은 성능을 보이는
Table 5의 시나리오 No. 1 (R
2 = 0.8365)은 가장 적은 은닉층 수(1개)와 노드수(6개)가 더 높은 정확도를 가진 예측모델을 도출할 수 있음을 보여준다. 따라서
Tables 5와
6의 결과는 데이터베이스의 특성과 예측변수의 수에 따라 최적의 성능을 보이는 은닉층 수와 노드수 산정이 가능함을 뜻한다.
본 연구에서는 시나리오 No. 3 (은닉층 수 = 1개, 노드수 = 36개)에서 가장 높은 R
2와 가장 낮은 RMSE가 나타났고 시나리오 No. 7 (은닉층 수 = 2개, 노드수 = 18-18개)에서 가장 높은 Fr 값이 나타났다. 이는 일반적으로 머신러닝 모델 예측 성능 평가에 이용되는 R
2과 RMSE가 적용성 측면에서 반드시 최고의 예측성능을 나타내지 않음을 뜻한다. 합리적인 투수계수의 예측은 0.1과 10배 안에 수렴되어야 하기 때문에 적용성 측면에서는 Fr값이 가장 높게 나타나는 시나리오 No. 7이 최적의 ANN 예측 모델로 판단된다.
Tables 5와
6에 나타난 Fr값은 더 높은 정확도의 투수계수 예측 평가를 위하여 더 좁은 예측범위 설정(e.g., 0.5와 2배 사이)을 통한 Fr값의 평가가 가능함을 뜻한다. 투수계수보다 더 낮은 불확실성을 보이는 흙의 물성치(e.g., 점착력, 내부마찰각, 단위중량, 비중) 예측 모델에서는 더 좁은 예측 범위 설정을 통한 머신러닝 예측모델의 성능평가가 필요할 것으로 사료된다.
4.2 흙의 종류에 따른 ANN 모델 성능 평가
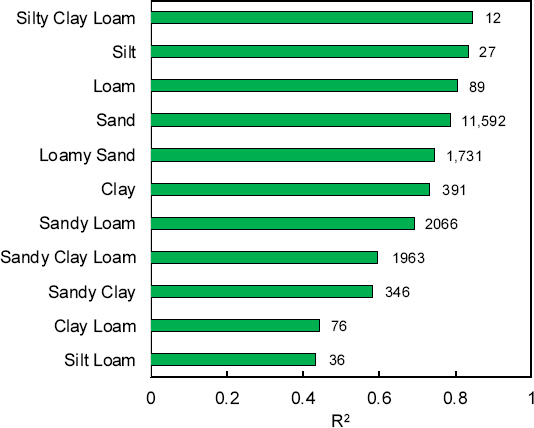
Fig. 5는 시나리오 No. 3에 대한 흙의 11가지 종류에 따른 모델의 R
2값을 나타낸다.
Fig. 5에 나타난 바와 같이 전체 데이터베이스를 이용하여 구축된 모델은 흙의 종류에 따라 다른 모델 성능을 보인다. Silt loam과 Clay loam에서 나타난 매우 낮은 모델 예측 성능은 Silt loam과 Clay loam에 해당하는 데이터가 ANN 모델의 성능에 부정적인 영향을 끼쳤음을 나타낸다.
Fig. 5에 나타난 성능이 낮은 soil texture는 데이터베이스에 상대적으로 적은 데이터 수를 점유하였다(Silt loam = 36개, Clay loam = 76개). 또한 높은 성능을 보이는 Sity clay loam, Silt, 그리고 Loam 역시 100개 미만의 상대적으로 적을 데이터 수를 가지기 때문에 구축된 ANN 모델에 대해 세 가지 soil texture가 반드시 상대적으로 높은 성능을 가진다고 할 수 없다. 따라서 모델의 성능을 높이고 모든 흙의 종류에서 높은 성능을 가지는 모델을 구축하기 위하여 상대적으로 적은 데이터 수를 가지는 흙에 대한 추가적인 데이터가 요구될 것으로 사료된다.
Fig. 5
Performance of ANN Model for 11 Soil Textures. Numbers Next to the Bar Indicate the Number of Data in Corresponding Soil Texture
5. 결 론
본 연구에서는 불확실성이 큰 지반의 포화투수계수 예측을 위한 ANN 예측 모델을 구축하였다. 모델 구축에는 11가지 흙에 대한 약 18,000개의 데이터를 이용하였고 다중공선성을 가지는 예측변수들을 제거한 4가지 예측변수를 적용한 예측 모델과 데이터베이스의 13가지의 예측 변수를 모두 적용한 예측모델을 은닉층, 노드수에 따른 10가지 시나리오에 대하여 구축하고 구축된 ANN 모델의 성능을 비교 및 분석하였다. 본 연구를 통하여 도출된 결론은 아래와 같다.
1) 본 연구에서 구축된 모든 시나리오에 대한 ANN 모델의 R2값은 0.767~0.836으로 은닉층과 노드수에 대하여 매우 광범위한 성능을 나타냈다. 이는 주어진 데이터베이스에 대한 ANN 모델의 하이퍼파라미터 최적화(hyperparameter optimization)의 중요성을 의미한다.
2) 모든 예측변수를 적용한 ANN 모델 구축 시 최적화된 은닉층과 노드수는 각각 2개와 [18개 18개]로 나타났다. 또한 VIF > 10의 예측변수를 제거한 ANN 모델의 최적화된 은닉층과 노드수는 각각 1개와 6개로 나타났다. 이는 예측변수의 수에 따라 최적화된 은닉층과 노드수를 산정해야함을 의미한다.
3) 본 연구에서 나타난 모든 예측변수를 적용한 ANN 모델의 더 높은 성능과 더 낮은 표준편차는 VIF > 10의 기준에 의거하여 다중공선성을 가지는 예측변수 제거가 모델의 성능이나 반복성에 부정적인 영향을 끼침을 보여준다.
4) 시나리오 No. 3에서 나타난 최적의 Fr값은 최적의 R2과 RMSE가 0.1과 10배의 합리적인 투수계수 예측 측면에서 반드시 최고의 예측성능을 나타내지 않음을 뜻한다.
5) 본 연구에서 이용된 데이터베이스의 다섯가지 soil texture는 100개 미만의 데이터를 가지기 때문에 ANN 모델의 적용성 증대를 위하여 향후 추가적인 데이터 확보 및 모델 재구축이 필요할 것으로 생각된다.
감사의 글
본 연구는 2022년도 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구(No. 2022R1C1C1007296)이며 이에 깊은 감사를 드립니다.
References
1. Agyare, W.A, Park, S.J, and Vlek, P.L.G (2007) Artificial neural network estimation of saturated hydraulic conductivity.
Vadose Zo. J, Vol. 6, pp. 423-431.


2. Alavi, A.H, and Gandomi, A.H (2011) Prediction of principal ground-motion parameters using a hybrid method coupling artificial neural networks and simulated annealing.
Comput. Struct, Vol. 89, pp. 2176-2194.

3. Babaoglu, Y, and Simms, P (2020) Improving hydraulic conductivity estimation for soft clayey soils, sediments, or tailings using predictors measured at high-void ratio.
J. Geotech. Geoenvironmental Eng, Vol. 146, pp. 06020016.

4. Cha, Y, Choi, W, and Buyukozturk, O (2017) Deep learning- based crack damage detection using convolutional neural networks.
Comput. Aided Civ. Infrastruct. Eng, Vol. 32, pp. 361-378.


5. Chapuis, R.P (2012) Predicting the saturated hydraulic conductivity of soils:A review.
Bull. Eng. Geol. Environ, Vol. 71, pp. 401-434.


6. Dolinar, B (2009) Predicting the hydraulic conductivity of saturated clays using plasticity-value correlations.
Appl. Clay Sci, Vol. 45, pp. 90-94.

7. Goh, A.T.C (1994) Nonlinear modelling in geotechnical engineering using neural networks.
Trans. Inst. Eng. Aust. Civ. Eng, Vol. 36, pp. 293-297.

8. Goh, A.T.C (1995) Empirical design in geotechnics using neural networks.
Geotechnique, Vol. 45, pp. 709-714.

9. Pachepsky, Y, and Park, Y (2015) Saturated hydraulic conductivity of US soils grouped according to textural class and bulk density.
Soil Sci. Soc. Am. J, Vol. 79, pp. 1094-1100.


10. Parasuraman, K, Elshorbagy, A, and Si, B.C (2006) Estimating saturated hydraulic conductivity in spatially variable fields using neural network ensembles.
Soil Sci. Soc. Am. J, Vol. 70, pp. 1851-1859.


11. Ren, X.W, and Santamarina, J.C (2018) The hydraulic conductivity of sediments:A pore size perspective.
Eng. Geol, Vol. 233, pp. 48-54.














