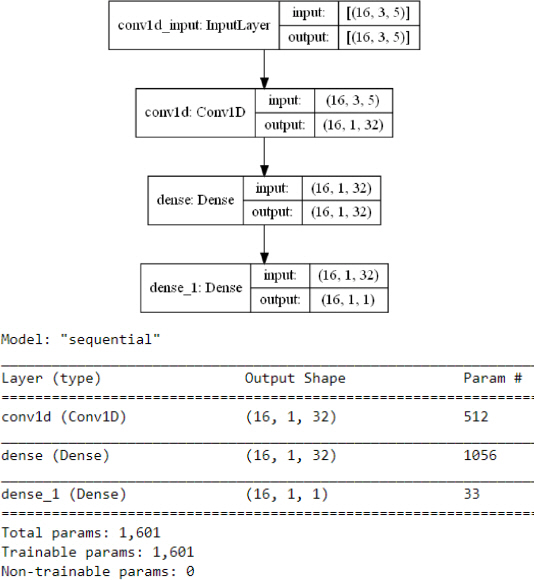
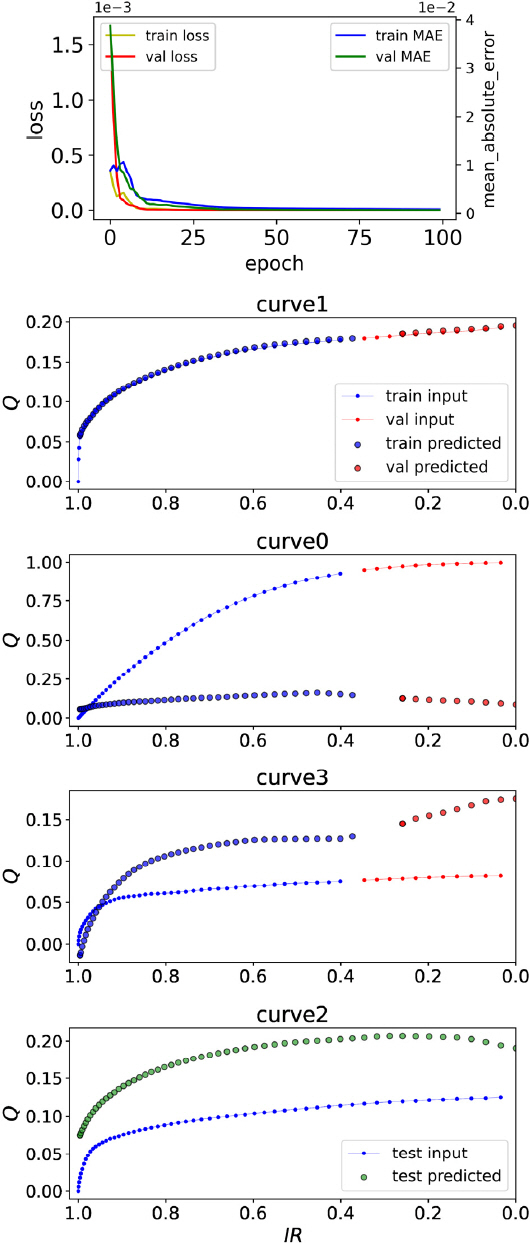
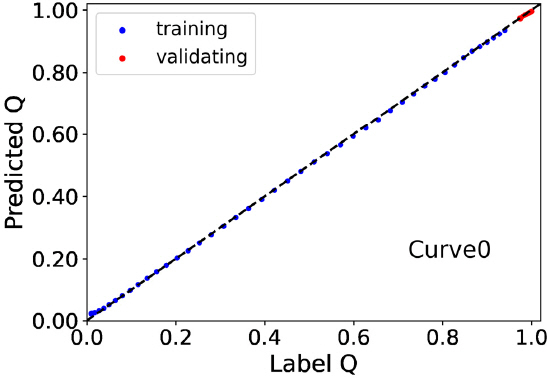
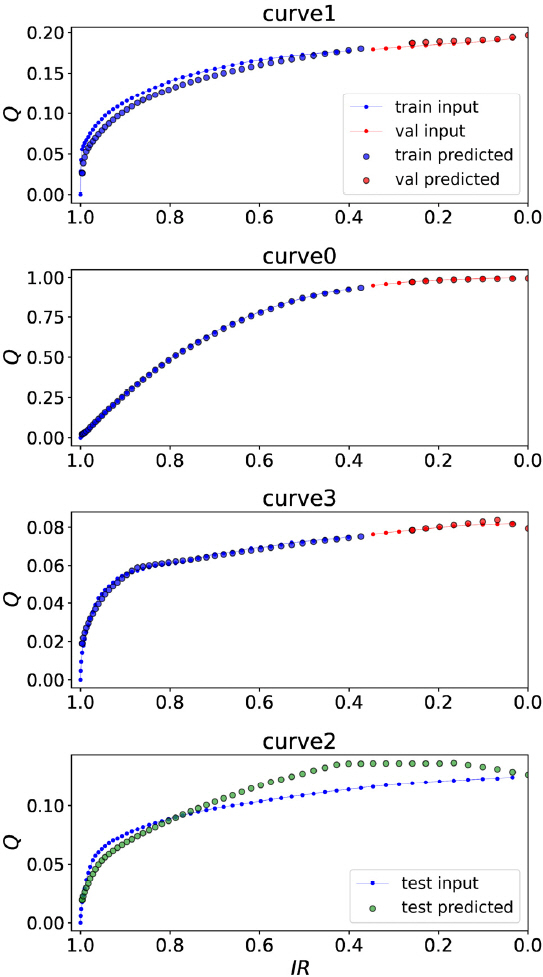
1. Abadi, M, Agarwal, A, Barham, P, Brevdo, E, Chen, Z, Citro, C, et al (2015)
TensorFlow:Large-Scale Machine Learning on Heterogeneous Systems. Software available from tensorflow.org.

2. Ahmadi, M.A, and Chen, Z (2019) Comparison of machine learning methods for estimating permeability and porosity of oil reservoirs via petro-physical logs.
Petroleum, Vol. 5, No. 3, pp. 271-284.

3. Blazejewski, R, and Murat-Blazejewska, S (1997) Soil clogging phenomena in constructed wetlands with subsurface flow.
Water Science and Technology, Vol. 35, No. 5, pp. 183-188.


4. Chew, A.W.Z, and Law, A.W.-K (2019) Feature engineering using homogenization theory with multiscale perturbation analysis for supervised model-based learning of physical clogging condition in seepage filters.
Journal of Computational Science, Vol. 32, pp. 21-35.

5. Chollet, F (2015)
Keras. Software available from keras.io.

6. Chollet, F (2018).
Deep learning with python. NY: Manning Publications.

7. Dramsch, J.S (2019).
Machine learning in 4D seismic data analysis:Deep neural networks in geophysics. Ph.D. dissertation, Technical University of Denmark, Lyngby, Denmark.

8. Du, X, Wang, Z, and Ye, X (2013) Potential clogging and dissolution effects during artificial recharge of groundwater using potable water.
Water Resources Management, Vol. 27, No. 10, pp. 3573-3583.


9. Géron, A (2019).
Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow:Concepts, Tools, and Techniques to Build Intelligent Systems. CA: O'Reilly Media, Inc.

10. Hua, G.F, Li, L, Zhao, Y.Q, Zhu, W, and Shen, J.Q (2013) An integrated model of substrate clogging in vertical flow constructed wetlands.
Journal of Environmental Management, Vol. 119, No. 5, pp. 67-75.


11. Lee, B.S (2021). Development of a deep learning model to estimate clogging of a stormwater infiltration filter.
Journal of Kore Academia-Industrial cooperation Society. in press.

12. Lee, B.S, Kim, L.H, Lee, K.H, Jeon, P.G, and Segismundo, E.Q (2014) Modeling of suspended solid clogging of porous media in urban stormwater infiltration facility.
Journal of Korean Society of Hazard Mitigation, Vol. 14, No. 6, pp. 427-437.


13. Lin, J, Kandra, H, Choudhury, T.A, and Barton, A (2018) Prediction of clogging in stormwater filters using artificial neural Network.
IEEE 27th International Symposium on Industrial Electronics (ISIE), pp. 771-776.

14. Meade, B, Khorshidi, H, Kandra, H, and Barton, A (2018) Regression modelling for prediction of clogging in non-vegetated stormwater filters.
10th International Conference on Water Sensitive Urban Design:Creating water sensitive communities (WSUD 2018 &Hydropolis 2018), pp. 233-240.

15. Segismundo, E.Q, Kim, L.-H, Jeong, S.-M, and Lee, B.-S (2017) A laboratory study on the filtration and clogging of the sand-bottom ash mixture for stormwater infiltration filter media.
Water, Vol. 9, No. 1, pp. 32.

16. Shahin, M.A (2014a) Load-settlement modeling of axially loaded steel driven piles using CPT-based recurrent neural networks.
Soils and Foundations, Vol. 54, No. 3, pp. 515-522.

17. Shahin, M.A (2014b) Load, settlement modeling of axially loaded drilled shafts using CPT-based recurrent neural networks.
International Journal of Geomechanics, Vol. 14, No. 6, pp. 06014012.

18. Sliwinski, K (2019).
A machine learning approach to predictively determine filter clogging in a ballast water treatment system. Master's thesis, Kth Royal Institute of Technology.

19. Wang, Y, Chen, J, and Larachi, F (2013) Modelling and simulation of trickle-bed reactors using computational fluid dynamics:A state-of-the-art review.
The Canadian Journal of Chemical Engineering, Vol. 91, No. 1, pp. 136-180.

20. Wei, X, Zhang, L, Yang, H.-Q, Zhang, L, and Yao, Y.-P (2020) Machine learning for pore-water pressure time-series prediction:Application of recurrent neural networks.
Geoscience Frontiers, Vol. 12, No. 1, pp. 453-467.

21. Wu, H, Fang, W.-Z, Kang, Q, Tao, W.-Q, and Qiao, R (2019) Predicting effective diffusivity of porous media from images by deep learning.
Scientific Reports, Vol. 9, No. 1, pp. 20387.




22. Zhou, J, Li, E, Wei, H, Li, C, Qiao, Q, and Armaghani, D.J (2019) Random forests and cubist algorithms for predicting shear strengths of rockfill materials.
Applied Sciences, Vol. 9, No. 8, pp. 1621.