기계학습을 이용한 효과적인 가뭄예측 성능평가
Performance Evaluation of Effective Drought Prediction Using Machine Learning
Article information
Abstract
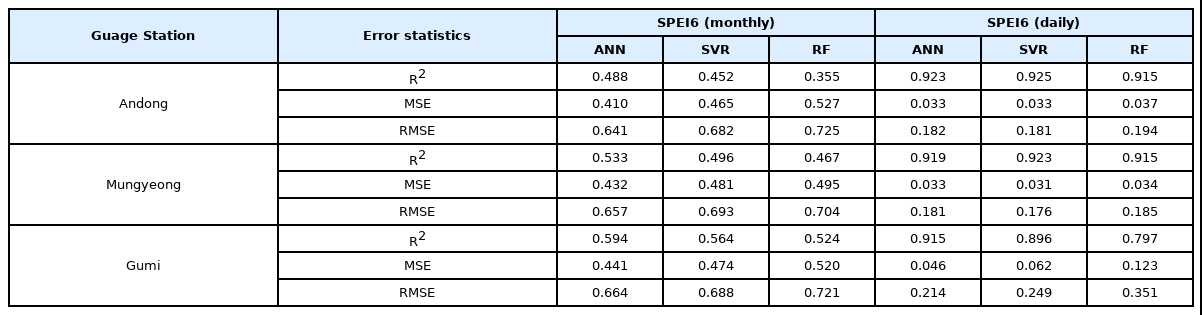
많은 연구자들이 가뭄예측을 높이는 연구를 지속적으로 이루어지고 있으나, 가뭄의 빈도와 패턴이 불규칙한 시계열을 가지고 있어 예측을 하기에는 한계가 있다. 가뭄은 복잡한 시계열을 가지고 있기에 하나의 모형으로만 예측하기도 어렵고, 다수의 모형으로 예측을 수행하여도 높은 예측이 나올 수 있다고 단정하기도 어렵다. 따라서, 강우, 기온, 일조량, 풍량 등과 같은 설명변수를 입력자료로 사용하여 예측을 높이는데 많은 연구들이 이루어지고 있다. 본 연구의 목적은 기상에서 일어나는 물리적인 현상을 기후자료를 이용하여 복잡하고 어려운 시계열 가뭄지수를 하나로 나타내는 표준강수증발산지수(SPEI)를 이용하여 가뭄예측 방법을 마련하고자 한다. 표준강수증발산지수는 강수량과 증발산량 자료를 이용하여 누적강수량에서 누적증발량을 제외하여 산정하는 방법이며, 증발산량은 월열지수법을 사용하였다. 기상청은 6개월 누적강수량 기준인 SPI6을 이용하여 기상가뭄을 평가하여, 본 연구에서도 월자료 및 일자료 SPEI6을 기준하여 기계학습에 적용하여 수행하였으며, 그 결과 ANN 월자료 R2는 안동 0.488, 문경 0.533, 구미 0.594, SVR 0.452, 0.496, 0.564, RF 0.355, 0.467, 0.524이며, 일자료는 ANN 0.923, 0.919, 0.915, SVR 0.925, 0.923, 0.896, RF 0.915, 0.915, 0.797로, 모든 지점에서 일자료 SPEI를 기계학습에 적용시 높은 예측을 수행하였음을 확인하였다.
Trans Abstract
There has been much research recently to improve the prediction of drought, but the frequency and pattern of drought displays an irregular time series that limits its predictability, making it difficult to predict with only a single model, and high-level predictions cannot be made even when many models are applied. Therefore, many studies have been conducted to improve predictions by using explanatory variables such as precipitation, temperature, sunshine duration, and air volume as input data. The purpose of this study is to devise a method for predicting drought using the Standard Precipitation Evaporation Index (SPEI), which represents a complex and difficult time series drought index using climate data for weather phenomena. The Standard Precipitation Evaporation Index is a method of calculating the cumulative precipitation by excluding the cumulative evaporation amount from the cumulative precipitation using precipitation and evapotranspiration data, and the evaporation amount is calculated using the monthly heat index method. The Meteorological Agency evaluated meteorological drought using SPI6, which is a 6-month cumulative precipitation standard, and applied it to machine learning based on monthly data and daily data SPEI6 in this study. As a result, ANN monthly data R2 was 0.488 in Andong and 0.533 in Mungyeong, Gumi 0.594, SVR 0.452, 0.496, 0.564, RF 0.355, 0.467, 0.524, and the daily data are ANN 0.923, 0.919, 0.915, SVR 0.925, 0.923, 0.896, RF 0.915, 0.915, 0.797, and the daily data SPEI at all points. It was confirmed that high prediction was obtained when machine learning was applied to these methods.
1. 서 론
가뭄은 평균이하의 강수량이 지속적으로 보이는 현상으로 물공급이 부족한 시기를 일컫는다(Lee and Woo, 2011). 그중 기상학적 가뭄은 주어진 기간의 강수량이나 무강수 계속일수 등으로 기상현상의 영향을 직접적으로 표현하는 가뭄을 말한다. 가뭄은 자연에서 무시할 수 없는 재해중의 하나이며, 상대적으로 장기간에 걸쳐 넓은 지역에 대해 발생하는 특성이 있다. 또한 가뭄은 홍수처럼 단기간에 발생하는 것이 아니라 서서히 다가오기 때문에 가뭄의 정도를 확실히 인식할 수 없어 사전에 대책을 수립하기 어려우며, 피해의 정도는 간접적이기는 하나 커다란 경제적인 손실을 일으킨다. 이처럼 가뭄은 뚜렷한 대책 없이 맞이할 경우 큰 피해를 발생하기 때문에 가뭄의 정도를 정량화 할 수 있는 가뭄지수를 가뭄 분석에서 많이 이용하고 있다.
가뭄을 예측하기 위한 학술적, 기술적 시도가 많은 학자들에 의해서 시도 되었으며, 가뭄을 예측하고 전망하는 방법은 시나리오에 기반을 두는 방법과 실시간으로 가뭄을 예측하는 비시나리오 기반의 방법으로 구분될 수 있다. 시나리오에 기반을 가뭄전망 방법은 기후변화 시나리오와 같은 미래의 기후 및 기상변화를 전망하고 이를 바탕으로 중기 혹은 장기적으로 가뭄의 발생 빈도와 함께 가뭄의 시공간적인 분포 특성을 전망하는 방법이다. 기후변화 시나리오 기반의 가뭄전망 연구의 경우 Kwon et al. (2009)은 3개월 General Circulation Model (GCM) 예측 결과를 바탕으로 2009년도 Palmer Drought Severity Index (PDSI) 가뭄지수를 산정하여 가뭄심도에 대한 단기예측을 실시하였다. 그리고 Ghosh and Mujumdar (2007)는 Standardized Precipitation Index (SPI)를 이용하여 10년 단위별 미래 가뭄전망을 실시하였다. 또한 Kim et al. (2013)은 GCM에 의해 생산된 기상전망 자료와 SPI를 이용한 빈도해석을 통해 Severity-Duration- frequency (SDF) 곡선을 유도한 후, 한반도의 확률가뭄 심도를 작성하여 미래 기후변화를 고려한 가뭄 취약지역을 제시한 바 있다. 한편, 비시나리오 기반으로 가뭄을 전망하는 방법은 통계학적 방법과 물리적 모델(physical model)에 기반을 둔 확정론적 수치해석 방법을 이용하여 실시간으로 단기 혹은 중기의 미래 가뭄을 예측하는 것이다. 가뭄을 통계학적 방법으로 예측하기 위해서 시도된 방법 중에서 가장 대표적인 방법은 다양한 수문시계열의 예측에 많이 활용되고 있는 ARIMA (Autoregressive Integrated Moving Average) 모델이다. 하지만 ARIMA모델은 기본적으로 예측하고자 하는 시계열의 정상성(stationarity)을 전제로 하는 선형모델이라는 점에서 비정상성(non-stationarity)과 비선형성(non-linearity)이 특징적인 수문시계열을 예측하는 데는 많은 한계를 갖고 있으며, 이분산성(heteroskedasticity)을 가질 경우, 효과적인 예측을 위해서는 관측치에 가중치를 부여함으로써 동일한 오차항 분산을 가지도록 해야 하는 문제점이 있다. 또한 Belayneh and Adamowski (2012)는 서포트 벡터 회귀(support vector regression, SVR)와 웨이블릿(wavelet neural network) 신경망을 이용하여 SPI를 예측하였으며, 최적모델구조는 root mean square error (RMSE), mean absolute error (MAE) 및 R (correlation Coefficient)를 통해 선정하였고, 1-6개월의 선행예보 시간을 갖고 가뭄을 전망하였다. 그리고 Paulo et al. (2005)은 SPI를 이용하여, 마코프 연쇄(Markov chain) 및 대수선형모델(log-linear model)을 적용하여 SPI기반 가뭄예측의 정확도를 검증하였으며, Bacanli and Fatih (2008)은 터키의 아나톨리아(Anatolia) 지역을 대상으로 뉴로퍼지모델(Neuro-Fuzzy)을 적용하여 1964-2006년 기간의 월평균 강수량과 SPI를 바탕으로 가뭄을 예측하였다.
하지만, 여러 연구자들의 노력에도 불구하고 가뭄예측은 예측의 정확도를 높여야 하는 요구가 커지고 있다. 가뭄은 시간적 공간적으로 부정적 영향을 미치는 자연재해로, 국내에서 발생하는 가뭄 빈도와 패턴이 불규칙적으로 변하며 지역별 강수량의 양극화가 심화됨에 따라 기존 월자료를 이용해서는 높은 예측값을 기대하기 어렵기 때문이다. 따라서, 본 연구에서는 복잡하고 비선형성으로 이루어진 가뭄 패턴을 기상학적 가뭄의 정도를 나타내는 표준강수증발지수(Standardized Precipitation Evapotranspiration Index, SPEI)인 월SPEI와 일SPEI를 기계학습모델에 적용하여 예측개선 모형을 개발하고자 한다.
2. 연구방법
2.1 잠재증발량
월열지수법(monthly heat index method)은 월별 잠재증발산량을 산정하기 위해 사용되는 방법으로 Thornthwaite (1948)에 의해 제안된 방법이다. Thornthwaite (1948)는 북위 29∼43° 사이의 미국 전역에 대해 증발산계 측정에 의해 자료를 수집한 후 기온 및 일조시간과 잠재증발산량 사이의 관계를 광범위하게 연구하였으며, 그 결과를 분석하여 Eq. (1)과 같은 경험적인 잠재증발산량 산정 공식을 제안하였다.
여기서, PEn은 월 단위 잠재증발산량(cm/month)이며, Ld는 위도에 따른 일조시간 조정계수, tn은 월평균기온(℃), J는 연열지수(yearly heat index)로 Eq. (2)를 이용하여 산정하였으며, a는 Eq. (3)의 관계를 통해 산정되는 계수이다.
월열지수법은 증발산량이 기온에 직접 비례한다는 점에 근거를 두고 있는 방법으로 실제 여러 가지 다양한 수문학적 인자들이 증발산에 영향을 미친다는 점에서 이론적인 약점이 없지 않으나 대체로 만족할만한 결과를 주는 것으로 알려져 있으며, 여러 가지 수자원 관련 계획 수립에 있어 잠재증발산량을 산정하기 위한 방법으로 이용되고 있다.
2.2 SPEI
Vicente-Serrano et al. (2010)은 인간의 영향을 배제하고 자연현상만으로 가뭄을 평가 할 경우, 강수량과 더불어 증발산량을 가뭄에 직접적으로 영향을 주는 인자로 판단하였으며, 이에 따라 강수량과 증발산량을 고려하는 새로운 가뭄지수인 SPEI를 제안하였다. SPEI는 강수량과 기온 인자를 사용하여 가뭄을 평가할 수 있다. 국내에서는 Kim et al. (2012)이 SPEI를 활용하여 국내 가뭄을 평가한 바 있다(Zhang et al., 2019). SPEI는 SPI와 마찬가지로 광범위한 기후에 대하여 계산될 수 있으므로 가뭄 심각도 시공간적으로 평가 할 수 있다. 또한 Keyantash and Dracup (2002)은 가뭄지수가 통계적으로 강력하고 쉽게 계산되어야 하며 명확하고 이해하기 쉬운 계산절차를 갖추어야 한다고 지적하였다. SPEI는 계산이 간단하며 원래 SPI 계산절차에 기초하여 계산된다. SPI는 입력 자료로서 월별 또는 주별 강우량을 사용하는 반면, SPEI는 강우량과 잠재증발산량의 월간 또는 주별 차이를 이용하는 차이점이 있다.
기상청에서 제공하고 있는 SPEI는 기온자료만을 사용하여 잠재증발량을 산정하는 Thornthwaite 방정식(월열지수법; Thornthwaite, 1948)을 사용하고 있으며, 본 연구에서도 이를 적용하여 산정하였다. 수분편차(Climatic water balance, Di)는 월강우량(Pi)에서 월잠재증발산량(PETi)을 뺀 것으로서 Eq. (4)와 같이 나타낼 수 있으며, SPEI는 Eq. (5)에 나타냈다. 또한, Table 1은 SPEI를 6등급으로 구분하여 나누었다.
P ≤ 0.5인 경우, P는 결정된 D값이며, P = 1 - F(x)를 초과할 확률이다. P > 0.5이면 P는 1 - P로 대체되고 그 결과 SPEI의 부호가 반전된다. 상수는 C0 = 2.515517, C1 = 0.802853, C2 = 0.010328, d1 = 1.432788, d2 = 0.189269, d3 = 0.001308이다. SPEI의 평균값은 0이고 표준 편차는 1이며, SPEI는 표준화된 변수이므로 시간과 공간에 따라 다른 SPEI 값과 비교할 수 있다. SPEI가 0이면 Log-logistic 분포에 따라 D누적 확률의 50%에 해당하는 값을 나타낸다.
2.3 전처리
기계학습 모델을 구축하는데 있어서 가장 중요한 단계중 하나는 입력변수를 선택하는 것이다. 본 연구에서는 입력변수에 대한 최적 지체시간을 결정하기 위하여 autocorrelation function (ACF)를 활용하였다(Seo et al., 2017). ACF는 시계열 자료의 자기상관성(시간에 따른 상관정도)을 파악하기 위한 함수로서, 시차에 따른 자기상관에 기초하여 최적 지체시간이 결정된다. ACF는 다음 Eq. (6)과 같이 나타낼 수 있다(Jo, 2017).
여기서,
또한, 자기상관분석시 고려해야 할 부분 중 하나는 경향성 즉, 트랜드(Trend), 계절성(Seasonality)이다. 경향성(Trend)는 시간이 흘러 지남에 따라 데이터(data)에 뚜렷하게 보이는 상하(上下) 추세가 있는지 그래프로 확인해야 한다. 무작위성(Random)한 그래프곡선 움직임에 있어서도 상승하는 추 세가 있을 수 있다. 트랜드 존재가 있느냐 없느냐에 따라 사용할 수 있는 모델이 달라질 수 있기 때문이다. 기상학적인 예로, 우리나라 특정 월별에 따라 비가 많이 내리거나, 특정 월별에 산불이 자주 일어난다거나, 하루기온 데이터 중 오후 2시가 가장 기온이 높다거나, 여름이 되면 기온이 높아지거나 겨울이 될 때마다 기온이 많이 내려가는 등 이런 경우를 말한다. 데이터 안에 이러한 계절적인 주기추세가 존재한다면 보다 나은 예측 결과를 기대할 수가 없다. 따라서, 이러한 시계열에서의 경향(Trend) 및 계절성(Seasonality)을 분해(Decompostion)로 변환해준다.
2.4 정규화
자료분석 과정에서 접하는 문제중 하나가 데이터자료 단위의 불일치이다. 단위 불일치에 따른 영향을 최소화 할 수 있는 방법에는 정규화(normalization)와 표준화(Standardization)가 대표적이다. 이러한 방법들은 2개 이상의 독립변수의 단위가 서로 다를 때 독립변수들을 동일한 스케일로 검토할 수 있게 한다. 즉, 다른 데이터자료와 같이 분석을 할 때 표준화 혹은 정규화된 데이터자료를 사용하면 단위 차이 혹은 정수 및 소숫점 같은 일정하지 않은 숫자를 일정하게 만들어 이용할 수 있다.
또한, 양이 많은 데이터자료를 처리함에 있어서 여러 가지 이유로 데이터자료의 범위를 혹은 분포를 일정 구간 내에 만들어 주는 과정은 반드시 필요한 일이다.
정규화(Normalization)는 데이터자료의 범위를 0에서 1사이로 변환함으로써 데이터분포를 재조정하는 방법이다. 정규화 변환은 Eq. (7)과 같이 나타낼 수 있다.
여기서, x*는 정규화된 자료, x는 원자료, xmin은 x의 최소값, xmax는 x의 최대값이다.
2.5 모델성능평가
기계학습 모델성능평가를 위한 통계학적 지표는 관측값과 예측값의 차이를 기반으로 한다. 모델평가지표중 오차를 표현하는 MSE, RMSE는 값이 작을수록 모델성능이 우수함을 나타낸다. 반면, 무차원 지표인 결정계수 R² 값이 클수록 모델성능이 우수함을 나타낸다.
2.5.1 MSE
Mean Squared Error (MSE)관측값과 예측값의 차이, 즉 편차를 제곱해 평균한 것이다. 다시말해, 편차제곱합을 자료값의 개수로 나눈 것으로서 Eq. (8)과 같이 나타낼 수 있다(Dawson and Wilby, 2001).
여기서, N은 자료의 개수, yi는 관측값,
2.5.2 RMSE
MSE은 오류차의 제곱을 구하기 때문에 실제 오차평균보다 값이 커지는 특성이 있고 사용된 자료의 단위에 제곱한 단위를 사용하는 단점이 있다. Root Mean Squared Error (RMSE)는 MSE에 제곱근을 취한 것으로서 Eq. (9)와 같이 나타낼 수 있다(Dawson and Wilby, 2001).
2.5.3 R2
R2(R Sqaure)는 관측값과 예측값의 전반적인 일치정도를 정량적으로 나타내는 지표로서 그 값이 1에 가까울수록 예측 정확도가 우수함을 의미한다. R2 는 Eq. (10)과 같이 나타낼 수 있다(Dawson and Wilby, 2001).
여기서,
3. 대상유역 및 모형적용
3.1 대상유역
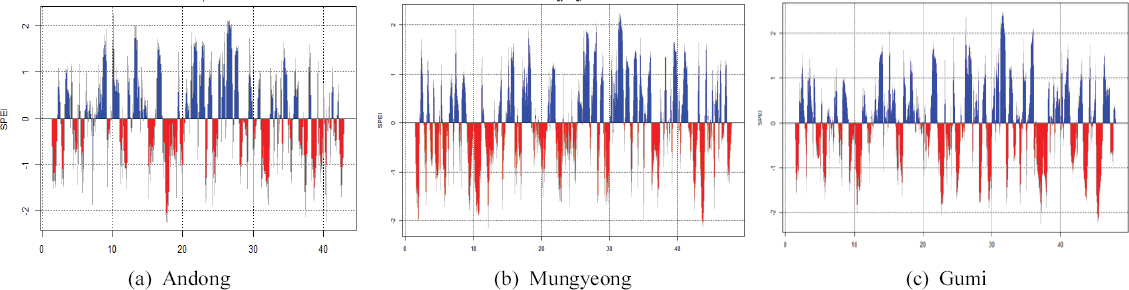
낙동강유역은 동서 폭이 약 180 ㎞, 남북 길이 120 ㎞ 가량인 낙동강유역의 면적은 23,384.2 ㎢로 한강의 유역면적에 비해 조금 뒤지지만, 총 하천길이는 510.4 ㎞로 남한에서는 가장 길며, 낙동강의 유역면적은 남한 전체면적의 약 1/4, 영남의 3/4쯤에 해당하는 면적이다. 안동, 문경, 구미는 낙동강유역의 대표적인 상류지역으로 안동은 2014년 전국적인 가뭄으로 강우량이 평년대비 30%에 그쳤으며, 문경은 2016년 저수지 평균저수율 45.7%, 구미는 2017년 평년대비 52%에 그쳤다. 따라서, 본 연구는 낙동강 중상류유역을 대상으로 가뭄예측을 하였으며. Fig. 1은 낙동강유역 상류지점을 나타냈다.
3.2 자료수집
가뭄예측을 위해 낙동강 중상류유역으로 안동, 문경, 구미관측소를 선정하였다. 우선, 증발산량 산정하기 위해 기상자료개방포털(https://data.kma.go.kr)에서 낙동강유역내 3개 지점인 안동, 문경, 구미관측소를 해당 연도에 대한 월별강우량, 월평균기온 등을 가뭄예측을 위해 관측소별로 안동은 1983년-2019년, 문경, 구미는 1973년-2019년까지 관측자료을 이용하였으며, 안동은 일부 기후 결측(1973년-1982년)으로 제외하여 정리하였다. 또한, 일자료 SPEI는 기상청 수문기상 가뭄정보 시스템에서 2018년4월부터 2020년 7월까지 제공받아 사용하였다.
본 연구에서는 표준가뭄지수를 6개월로 분석기간을 구분하여 SPEI6으로 3개 지점에 대하여 가뭄 산정을 하였다. 앞서 설명한 가용자료를 활용하여 SPEI6 가뭄지수에 적용할 증발산량을 산정하기 위한 입력자료인 월강우량, 월평균기온, 일최대 및 일최저기온 등을 자료 수집하여, Thornthwaite (1948)법에 적용하였다. Fig. 2는 안동, 문경, 구미지점에 대한 SPEI를 나타내고 있으며, 전체기간 중 –1.0 이하(-1.0 ≤ Weak drought)를 기준으로 각 지점별 가뭄시계열을 차지하는 비율을 살펴보면 안동 18.2%, 문경 16.8%, 구미 17.9%로 나타났다.
3.3 모형적용
3.3.1 ANN
인공신경망은 다양한 상황에 적용된다. neuralnet은 회귀 분석의 문맥에서 다층퍼셉트론(multi-layer perceptrons)을 생성한다. 공변량(covariates)과 응답 변수 간에 함수 관계를 근사화하여, 신경망은 일반화 선형 모델의 확장으로 사용된다. 공변량(또한 입력 변수) 그리고 응답변수(또한 출력변수) 간에 함수적 관계에 큰 관심을 가진다. 일반화 선형 모델과 달리(generalized linear models, GLM; McCullagh and Nelder, 1983), 선형 조합에서 처럼 공변량과 응답변수 간의 관계 타입을 사전에 명시할 필요가 없다. 인공 신경망을 가치있는 통계적 도구로 만든다. 관측 데이터는 신경망 훈련에 사용되고 신경망은 변수를 반복적용하여 근사적인 관계를 학습한다. neuralnet은 회귀 분석의 맥락에서 신경망을 훈련하기 위해 만들어 졌다. 그러므로, 탄력적 역전파(backpropagation)가 사용되었고, 이 알고리즘은 가장 빠른 알고리즘의 하나이다(e.g. Schiffmann et al., 1994). 전통적인 역전파는 비교 목적으로 포함되었으며, 활성화 및 에러 함수를 사용자가 선택함으로써 패키지는 매우 유연하다. 사용자는 몇 개의 은닉층(hidden layers) 사용이 가능하다. 여분의 은닉층을 포함하여 계산 비용을 줄일 수 있다.
3.3.2 SVR
SVR은 Support Vector Regression을 훈련시키는데 사용된다. 일반 회귀(regression)를 수행하는 데 사용할 수 있으며, 분류(classification)와 밀도 추정에도 사용된다. SVR은 일반 회귀를 수행하는 데 사용할 수 있으며 nu-regression은 분류, epsilon-regression은 회귀로 계산을 할 수 있다. 본 연구에서는 회귀예측을 위해 SVR을 epsilon-regression로 분석하였다. 아울러, SVR 예측은 R에서 “e1071” packages로 사용하였다.
3.3.3 RF
Decision Tree의 단점을 보완한 모델이 Random Forest로, 배깅(bagging) 기법을 이용하여 forest를 구성하는 각 Decision Tree에 무작위성(randomness)을 부여하고, 이를 통해 각 Decision Tree의 예측 결과가 비상관화(decorrelation)되게 하여, 결과적으로 일반화 성능을 향상시킨다(Breiman, 2001). 배깅은 부트스트랩(bootstrap) 방법을 통해 생성된 조금씩 다른 훈련 데이터를 이용하여 학습된 기본 모델들을 결합(aggregating)시키는 기법이다(Breiman, 1996). 부트스트랩이란 입력된 데이터로부터 중복을 허용하여 입력 데이터와 같은 크기를 갖는 새로운 데이터 세트를 생성하는 기법을 말한다.
3.3.4 입력변수
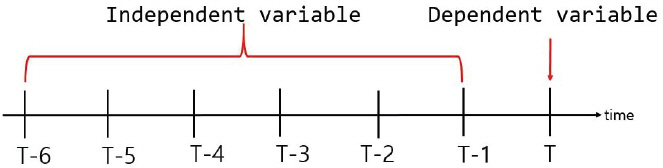
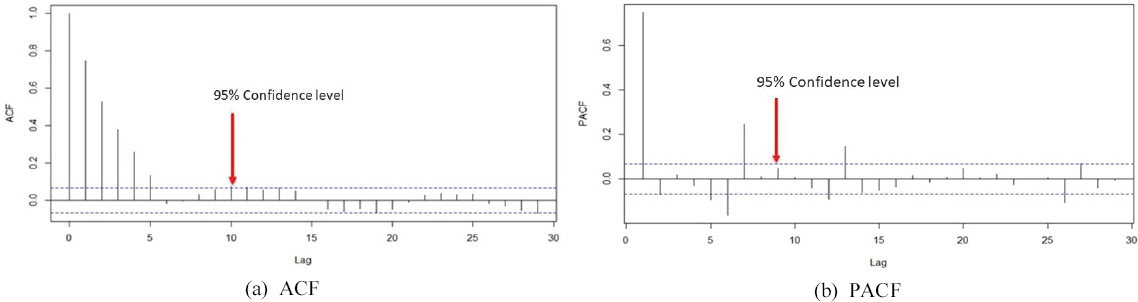
SPEI지수가 시계열 자료임을 고려해 과거시차를 고려한 자료로 과거시차의 독립변수로 현재시점의 종속변수를 예측하는 자료형태이다. 자료의 특성과 연구 목적에 따라 독립변수로 사용할 시점을 결정하는 것은 중요하며, 보통 전문가의 의견이나 연구자의 경험에 의해 결정한다. 시계열 자료의 특성상 예측하고자하는 시점으로부터 시차가 클수록 영향력이 감소한다. 따라서 적절한 시차를 고려한 독립변수 시점을 찾는 것이 중요하다(Jang and Cha, 2017). Fig. 3은 과거시차를 6개월로 지정하였을 때 L1(리드타임)으로 하여, t시점을 종속변수로 t-1, t-2, t-3, …, t-6 시점을 독립변수로 자료를 구축하여 모델에 입력자료로 사용하였다. 각 기계학습 모델별 Input자료는 월자료 및 일자료 SPEI6을 사용하였다. Fig. 4는 ACF 및 PACF를 분석하여 SPEI 시차를 결정하였다. 분석결과 6번째 시점에서 자기상관관계가 가장 크게 나타났다. 기계학습 예측을 위해 SPEI6을 입력자료로 Trainset 70%, Testset 30%를 나누어 설정하였으며, 월자료SPEI6은 각 지점별 데이터개수가 관측개시일이 상이하여 안동 444개, 문경, 구미는 각각 564개이며, 일자료SPEI6은 822개(2018년 4월부터 2020년 7월)를 사용하였다.
3.3.5 매개변수 결정
기계학습모델 개발에서 가장 중요한 단계 중 하나는 최적 학습매개변수를 결정하는 것이다.
ANN 모델링의 경우, 은닉뉴런 개수의 결정이 가장 중요하다. ANN 모델의 성능은 은닉뉴런의 개수에 영향을 받는다. ANN은 MLP 타입을 채택하였으며, 모델은 하나의 은닉층을 가지는 3층 구조, 즉 입력층, 은닉층, 출력층으로 구성되었다. 활성화 함수로서 losistic함수가 사용되었으며, 역전파알고리즘을 이용하여 모델을 학습하였다.
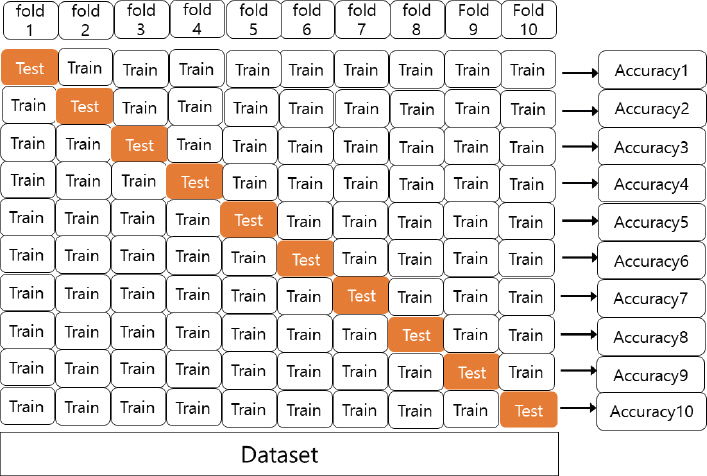
SVR 모델링에서의 핵심은 최적 학습매개변수의 결정이다. 본 연구에서는 그리드 탐색방법을 이용하여 SVR의 3가지 학습매개변수(커널매개변수, 무감도손실함수 매개변수, 정칙화 매개변수)의 최적값을 결정하였다. SVR 모델을 구축하기 위해서는 먼저 적절한 커널함수가 사전에 선택되어야 한다. 본 연구에서는 시행착오적 접근을 통해 커널함수로서 RBF함수를 선택하였다. 이러한 학습매개변수들은 상호의존적이기 때문에 SVR 모델에 대한 양호한 성능을 얻기 위해서는 최적화 알고리즘을 통하여 최적 학습매개변수 값을 결정하는 것이 필수적이다(Seo, 2015). 따라서 본 연구에서는 학습매개변수 값을 결정하기 위하여 그리드 탐색기 법을 적용하였다. 일반적인 K-겹 교차검증법(k-Fold Cross Validation)은 Traindataset에 같은 크기의 k개의 그룹을 Fold 혹은 겹이라고 하는데 이를 k개의 폴더로 나누고 (k-1)개의 Test Fold와 1개의 Validation Fold로 구성한 후, 이를 총 k회 만큼 검증(Validation)을 한다. 각 검증을 시도할 때 마다 Test Fold를 Fig. 5처럼 다른 섹션으로 넘어가서 성능 평가를 한다. 이렇듯 각 k회 검증이 끝나게 되면 각 하이퍼파라미터(Hyperparameter)에 대한 검증 결과 모두 합쳐 평균으로 구하여 최종 Hyperparameters를 튜닝(tuning)하게 된다. 하지만, 데이터가 작을 경우 앞서 말한 Train, Validation, Test의 세분류로 한 것 보다, Train, Test 두분류만 할 때 학습데이터셋이 더 늘어난다. 즉, 데이터 수가 작은데 Validation과 Test에 더 많이 나누어지면, 과소적합(underfititing)으로 모델학습이 저하되는 현상이 나타난다. 따라서, 본 연구는 Traindata와 Testdata로 나누어 모델성능평가 하였으며, k = 10으로 하여 K-겹 교차검증을 실시하였다. Eq. (11)과 Fig. 4는 k-겹 교차검증에 대한 식과 그림을 나타낸다.
3.3.6 기계학습적용
앞서 기술한 기계학습에 월SPEI와 일SPEI를 관측값과 예측값으로 비교하여 각 지점별로 Fig. 6과 같이 나타냈다. 또한, Table 2는 정량적 평가를 위해 관측값과 예측값의 R2, MSE, RMSE를 산정하여 나타내었다. 그 결과 ANN 월자료 R2는 안동, 문경, 구미 순으로 0.488, 0.533, 0.594, SVR 0.452, 0.496, 0.564, RF 0.355, 0.467, 0.524, MSE는 ANN 0.410, 0.432, 0.441, SVR 0.465, 0.481, 0.474, RF 0.527, 0.495, 0.520, RMSE는 ANN 0.641, 0.657, 0.664, SVR 0.682, 0.693, 0.688, RF 0.725, 0.704, 0.721로 나타났다. 일자료는 ANN기준 R2 0.923, 0.919, 0.915, SVR 0.925, 0.923, 0.896, RF 0.915, 0.915, 0.797, MSE는 0.033, 0.033, 0.046, SVR 0.033, 0.031, 0.062, RF 0.037, 0.034, 0.123, RMSE는 0.182, 0.181, 0.214, SVR 0.181, 0.176, 0.249, RF 0.194, 0.185, 0.351로 각각 나타나 일자료 기계학습시 확률오차를 나타내는 MSE, RMSE는 모든 지점에서 낮게 나타났으며, R2은 높게 나타났다.
4. 결 론
본 연구에서는 월 및 일자료 SPEI를 이용하여 효과적으로 예측하기 위한 기계학습모델의 성능평가를 실시하였다. 제시된 가뭄지수는 SPEI6 시계열에 대한 유효성 검사 데이터 세트에서 얻었다. 사용된 예측모델인 ANN, SVR, RF를 낙동강 중상류지점인 안동, 문경, 구미를 선정하여 가뭄예측을 분석하였다. 월자료SPEI에서는 ANN모델이 가장 높은성능을 보였으나, 일자료SPEI에서는 안동과 문경지점에서 SVR 예측값이 모델성능평가 지표에 기초하여 우수한 것으로 나타났으며, 구미지점은 ANN이 높은 예측값을 나타났다. 월자료와 일자료의 성능평가 차가 큰 이유는 SPEI 월자료와 일자료로 모델예측시 시계열의 연속성이 중요하다는 것을 의미한다. 기계학습에 있어서 가장 중요한 요소 중에 하나가 양질의 데이터이다. 양질의 데이터가 풍부해야만 반복 학습을 통해 높은 오차를 줄일 수 있으며, 그로 인해 높은 예측을 기대할 수 있다. 월평균값을 하나의 시계열데이터를 만들어, 예측모델을 했을 경우 시간에 따른 연속성은 가지나 월별에 따른 편차가 크기 때문에 일자료 보다 높은 예측값을 기대하기는 어렵다. 이는 다른 지점도 동일한 이유로 월자료의 예측은 감소로 나타난다. 본 연구의 주요 결과는 다음과 같다.
(1) 기존 월자료 가뭄지수를 사용하여 예측을 높이는 연구가 이루어지고 있으나, 성능평가에서는 여전히 낮은 예측에 고전하고 있다. 국내에서 발생하는 가뭄 빈도와 패턴이 불규칙적으로 변하며 지역별 강수량의 양극화가 심화됨에 따라 기존 월자료를 이용해서는 높은 예측값을 기대하기 어렵다. 따라서, 본 연구에서는 SPEI 월자료와 일자료를 기계학습에 적용하여 이를 성능평가 하여 나타냈다.
(2) 전반적으로, 월자료 사용하여 기계학습을 하였을 경우 ANN이 3개지점 모두 높은 것으로 나타났으며, 일자료는 구미 ANN이, 안동, 문경지점은 SVR 예측값이 최상의 결과를 제공하는 것으로 나타났다. 일자료 예측값이 월자료 예측값 보다 모든 지점에서 R2가 높은 것으로 나타났으며, 확률오차 통계인RMSE, MSE도 일자료가 항상 낮았고, RF는 모든 지점에서 ANN, SVR보단 모델성능분석에서 비교적 낮게 나타났지만, 월자료와 비교시 모델성능평가에서는 모두 높은 예측력을 나타났다. 특히, 안동, 문경지점의 경우 SVR이 성능평가에서 높게 나온 이유는 전형적인 방법론인 ANN이 과도한 학습으로 과대적합의 문제가 발생할 수 있어 이러한 단점을 보안한 방법인 SVR이 높은 예측을 한 것으로 사료된다.
(3) 일반적으로 기계학습을 할 때, 입력자료를 원시상태에서 입력하여 높은 예측력을 기대하기 어려웠으나, 전처리 과정에서 분해로 SPEI 시계열을 ‘잡음 제거’하여 원래의 SPEI 시계열을 전처리함으로써 ANN, SVR, RF가 잡음 없이 주요 신호를 모델링 할 수 있도록 함으로써 모델이 정확한 결과를 제공할 수 있었다.
감사의 글
본 결과물은 환경부의 재원으로 한국환경산업기술원의 물관리연구사업의 지원을 받아 연구되었습니다(79608).