1. 서 론
원자력발전소(이하, 원전) 확률론적 화재 리스크 평가 방법인 화재 PRA (Fire Probabilistic Risk Assessment)는 원전에서 발생한 화재로 인한 잠재적 영향을 확률론적으로 분석 및 평가하는 것으로 원전의 설계, 배치, 운전 등 종합적이고 전반적인 자료를 바탕으로 원전 내 특정 지역에서의 화재발생 가능성, 화재 확산, 화재 감지 및 진압, 안전관련 케이블과 기기에 대한 화재 영향 및 손상 확률 등을 고려하여 원전의 리스크 평가 척도인 노심손상빈도(Core Damage Frequency, CDF)와 방사능 대량방출빈도(Large Release Frequency, LRF) 도출과 함께 설계취약점 및 원전 리스크 감소를 위한 안전성향상 방안을 제시하는 종합적이며 체계적인 원전 화재의 정량적 리스크 평가 기법이다(IAEA, 1998; Park and Ha, 2003; NRC, 2005; NFPA, 2006).
현행 원전 화재 PRA 방법론은 미국 원자력규제위원회(Nuclear Regulatory Commission, NRC)와 미국 전력연구원(Electric Power Research Institute, EPRI)이 공동으로 개발한 NUREG/CR–6850 (NRC, 2005)으로, 리스크 정보 성능기반(Risk Informed Performance Based, RIPB) 화재방호 프로그램인 NFPA 805 (NFPA, 2006)의 정량적 리스크 평가에 기초한 의사결정(Decision Making) 지원을 위해 전기캐비닛, 모터, 펌프, 변압기 등 미국 원전의 실제 화재사건 경험에 기반한 다양한 점화원(Ignition Source)들의 화재 특성을 반영하여 화재 시 안전관련 기기 및 케이블에 미치는 위험의 정도를 평가하기 위해 기존 화재 PRA 방법론인 Fire PRA Implementation Guide (EPRI, 1995)의 보수성(Conservatism) 저감 및 분석 현실성(Realism) 향상을 위해 원전 및 화재 관련 최신 기술을 집약시킨 최신 분석 방법론이다(NRC, 2005; Floyd et al., 2020).
이와 같이 NUREG/CR-6850 개발의 주요 목표중의 하나였던 화재 PRA의 분석 현실성(Realism) 확보 및 향상(Floyd et al., 2020)은 의사결정자(Decision Maker)의 화재 리스크 발생원(Source) 및 결과(Consequence)에 대한 정확한 이해에 기초한 의사결정 지원을 통하여 원전 안전시설에 대한 과대/과소 안전여유도(Safety Margin)로 인한 손실 및 피해를 최소화 하고 불필요한 운전 및 보수비용을 줄이도록 하는 의사결정 지원모델의 신뢰성 확보를 위한 필수적 요소이다(EPRI, 1995; Worrell and Rochon, 2015).
이러한 이유로 화재 PRA가 원전에 최초로 적용된 WASH- 1400 Appendix XI(NRC, 1975; Kazarians and Apostolakis, 1978) 이후 현재까지, 화재 PRA 분석 현실성(Realism) 확보를 위한 연구들이 화재실험에 기초한 상세 화재모델링(Fire Modeling) 지원을 위한 연구(NRC, 2008a, 2008b, 2008c, 2012a, 2012b, 2016, 2020a, 2020b)와 실제 화재 경험데이터를 활용한 연구를 중심으로 계속적으로 수행되고 있다(EPRI, 2009, 2011; NRC, 2015).
그러나 대부분의 이러한 연구들은 실험에 기초한 화재모델링 지원을 위한 연구에 집중되어 있으며, 화재사건 데이터를 활용한 연구는 부분적으로 수행되고는 있으나 이 또한 화재발생빈도를 중심으로 수행되고 있는 상황이다.
화재발생 빈도 관련 연구 이외에는, 일부 현행 화재 PRA 방법론에서 제안하고 있는 소방대진압실패 지수(Exponential) 확률모형의 모수(Parameter) 추정 관련 연구가 수행된 적이 있으나 이 또한 활발하게 진행되고 있지 못한 실정이다(NEI, 2010; NRC, 2015).
소방대 진압실패 확률모형은 화재 PRA를 통한 화재 리스크 도출시 화재에 의해 안전정지(Safe Shutdown) 및 사고완화(Mitigation) 관련 케이블 및 기기가 손상되기 전에 소방대에 의해 수동으로 화재 진압을 실패할 확률값을 도출하기 위한 확률모형으로, 노심손상빈도(CDF)에 기여하는 정도가 38.7%에 이를 정도로 원전 화재 리스크 결과에 미치는 영향이 크다(Lee and Park, 2019).
따라서 현실적(Realistic) 화재 특성이 반영되지 못한 소방대 진압실패 확률모형은 화재 리스크 기여도가 큰 중요 화재 시나리오 우선순위 도출의 왜곡을 초래하여 최적 화재방호 대응 전략 수립을 위한 리스크 정보 성능기반(RIPB) 화재방호 프로그램 적용시 신뢰성을 저하시킬 수 있어(Siu et al., 2012, 2016), 실제 화재 특성이 반영된 최적 소방대 진압실패 확률모형 개발은 필수적이다(NEI, 2010).
그러나 이제까지 국내⋅외에서는 원전 화재 고유 특성을 반영한 화재 PRA 분석 현실성(Realism) 확보 및 향상을 위한 소방대 진압실패확률 모형의 최적화를 위한 연구가 수행된 적이 없다.
이에 본 연구는 원전 화재사건 데이터를 활용하여 원전 화재 리스크 기여도가 가장 큰 전기화재를 중심으로 소방대 진압실패 확률모형을 최우추정법(Maximum Likelihood Estimation, MLE)을 이용하여 추정하고, 이의 적합성을 평가하여 실제 화재사건 경험을 현실적으로 반영할 수 있는 최적화된 확률모형을 도출함으로서 정량적 원전 화재 리스크 평가 기법인 화재 PRA 분석의 현실성(Realism) 확보 및 향상에 기여하고자 한다.
2. 이론적 배경
2.1 화재 PRA 개념
2.1.1 화재 PRA 현황
원전 화재 PRA는 화재로 인한 원전 안전에 기여도가 높은 시나리오를 식별하고 그 발생 가능성(Likelihood)과 영향(Consequence)을 정량적으로 평가하여 리스크 기여에 따른 화재 시나리오별 우선순위를 결정하여 화재로 인한 원전 취약점을 도출하고 이에 대한 안전성 향상방안을 제시하는데 그 목적이 있다(Lee and Yang, 2003; NEI, 2010; Worrell and Rochon, 2015).
화재 PRA에서 고려하고 있는 리스크는 화재로 인하여 노심(Core)이 용융 될 수 있는 빈도인 노심손상빈도(CDF)와 화재로 인하여 노심이 용융된 후 원자로건물내의 방사능이 환경으로 유출될 수 있는 방사능 대량방출빈도(LRF)로 평가된다(IAEA, 1998; Park and Ha, 2003; NRC, 2005).
이와 같은 화재 리스크 평가 척도는 Eqs. (1), (2)와 같이 개별 시나리오별 노심손상빈도와 개별 시나리오별 방사능 대량방출빈도의 합으로 각각 구할 수 있다.
여기서, CDFscenario는 시나리오별 노심손상빈도, LRFscenario는 시나리오별 대량방출빈도를 의미한다.
이때, 각 개별 시나리오별 노심손상빈도와 대량방출빈도는 Eqs. (3), (4)와 같이 계산된다.
여기서, IF는 점화원의 화재발생빈도, W는 가중치, SF화재심각도(Fire Severity), Pns는 소방대 진압실패 확률, CCDP는 조건부 노심손상확률(Conditional Core Damage Probability), CLRP는 조건부 대량방출빈도(Conditional Large Release Frequency)를 의미한다.
2.1.2 화재 PRA 현실성(Realism) 확보의 중요성
화재 PRA를 통하여 도출된 리스크 결과인 노심손상빈도(CDF)와 대량방출빈도(LRF) 및 그 기여도에 따른 개별 중요 화재시나리오는 일반적으로 원전 운영자와 규제자가 각각 직면하게 되는 안전 관련 자원의 우선순위 결정 및 효율적 배분 문제와 화재방호 관련 발전소 변경사항들의 허용 관련 문제 등에 대한 의사결정(Decision Making) 지원 모델로서 중요한 역할을 수행한다(Siu et al., 2012).
따라서 화재 PRA가 충분한 현실성(Realism)을 확보하지 못한다면 리스크 정보에 기반한 의사결정 결과는 원전 현실을 반영하지 못한 편의(Biased)된 결과를 유발 하여 부적절한 안전관련 자원 배분과 허용되어서는 안될 운전 및 설계사항의 변경으로 예기치 못한 더 큰 안전 문제를 야기할 수 있어(Siu et al., 2012), 화재 PRA 분석에 있어서 현실성(Realism) 확보 및 향상은 중요하다.
2.2 소방대 화재 진압실패 확률 모형
소방대 진압실패 확률모형은 안전정지 및 사고완화 관련 기기와 케이블 등이 화재 영향에 의해 손상되기 전에 소방대에 의해 화재가 진압되지 못할 확률(Pns)을 모형화한 것(NRC, 2005)으로, Eqs. (3), (4)와 같이 시나리오별 노심손상
빈도(CDFscenario) 및 방사능 대량방출빈도(LRFscenario)를 도출하는데 있어서, 화재가 확산되어 주변 이차 가연물에 영향을 줄 수 있는 정도를 확률적으로 평가하는 화재심각도(Fire Severity)와 함께 화재 리스크 도출시 필수적 고려 대상이다(NEI, 2010). 또한 소방대에 의한 수동 화재진압 실패시 화재발생 구역뿐만 아니라 인접구역으로의 화재확산으로 손상 대상 안전정지 및 사고 완화 기기 범위의 확대로 원전 화재 리스크 증가를 유발하게 된다(Jee et al., 2013).
미국 NRC는 화재 PRA를 이용한 원전 화재 리스크 평가를 위해 지수(Exponential) 확률모형에 기초한 소방대 진압실패 확률모형을 제안하고 있으나, 실제 화재사건 경험 데이터의 고유 특성을 반영한 확률분포를 직접 적합 시켜 최적화된 소방대 진압실패 확률모형을 도출한 것이 아닌, 신뢰도 고장율 함수를 기반으로 t시간까지의 화재진압 실패 모형을 Eq. (5)와 같이 가정하고, λ(s)를 시간의 함수가 아닌 상수, 즉 시간에 일정한 평균 진압율인λ로 단순화시킨 Eq. (6)을 소방대 진압실패 확률모형으로 제안(NRC, 2005, 2015; Elicson et al., 2011)하고 있어, 원전 화재 경험이 반영된 현실성(Realism) 확보에 한계가 있다.
시간의 함수가 아닌 상수로 단순화시켜 가정된 지수 확률 모형의 모수(Parameter)인 평균진압률λ는 총 화재진압시간(min.)을 기준으로 화재발생 건수를 나눈 값으로, 현재 화재 PRA 방법론에서는 1968년부터 2009년까지 1,057건의 미국 원전 화재사건 데이터를 기초로 Table 1과 같이 화재특성에 따라 13개의 범주로 구분하여 각 범주별로 평균진압율λ를 제시하고 있다. 그러나 시간의 증가에 따라 화재 진압 확률이 단조 감소하는 지수 확률모형으로 단순화함에 따라 진압확률의 증가 혹은 감소의 추세를 보이는 현실적(Realistic) 화재사건 경험을 반영하지 못하는 제약이 있다.
Table 1
Non-Suppression Failure Probability Parameters (NRC, 2015)
여기서,Ts는 화재 진압 시간에 대한 확률변수,t는 화재가 감지되고 진압되는데 걸린 시간,는λ(s)시간 t에 종속적인 화재진압율을 의미한다.
특히 화재진압시간에 대한 확률변수Ts는 Fig. 2와 같이 소방대가 소화약제 분사를 시작할 때까지의 시간인Tf를 포함하며 화재발생 후 부터 감지까지 걸린 시간인Td는 제외된다(EPRI, 2015).
2.3 최우추정법(MLE)
확률분포의 모수(Paramter) 추정법에는 일반적으로 적률추정법(Method of Moment Estimation, MME), L-적률추정법(L-moment Estimation, LME), 확률가중적률법(Probability Weighed Moment, PWM) 그리고 최우추정법(Maximum Likelihood Estimation, MLE) 등이 있다(Oh, 2007; Lee, 2018).
적률관련 추정법들은 모수 추정량을 구하는 방법이 직관적이고 과정이 간단하여 초기 추정량으로 많이 이용되지만 타당성이 없는 추정값이 나타날 수 있거나 모수의 갯 수 만큼 적률이 존재하지 않아 적률법에 의한 추정이 불가능한 경우가 발생할 수 있다(Huh and Song, 2013).
이와 달리, 최우추정법(MLE)은 우도함수(Likelihood Function)를 기초로 표본자료가 나올 수 있는 확률이 최대가 되도록 하는 모수(Parameter)를 추정하는 방법으로서, 다른 방법에 비하여 추정량을 구하기가 용이하고 표본 크기가 클 때 모수 근처에서 정규분포에 따르는 특징이 있다. 그러나 최대우도(Maximum Likelihood) 값을 찾을 때 까지 많은 반복 작업을 필요로 하며, 해를 구하는 절차가 복잡하여 수렵하지 않아 적률추정법등에 비해 해를 구하지 못할 경우가 있고, 표본의 크기가 작을 때는 추정치에 편의(Bias)가 발생할 수 있는 단점이 있다. 하지만 일반적으로 가장 효율적인 추정을 구할 수 있는 방법으로 알려져 있어(Mood et al., 1974; Lee, 2003; Oh, 2007; Tan, 2009) 본 연구에서는 도출된 확률모형의 모수 추정을 위해 최우추정법(MLE)을 적용하였다.
Fisher (1925)에 의해 점추정량(Point Estimate)을 구하는 방법의 하나로 개발된 이와 같은 최우추정법(MLE)은 우주항공, 원자력분야 등의 신뢰도 연구 분야뿐만 아니라 금융, 전자, 통신 등 다양 분야에서 폭넓게 사용되고 있는 모수 추정 방법으로 주어진 표본자료에 대한 매개변수의 최우추정량(MLE)은 표본의 확률 또는 확률밀도를 극대화 하는 매개변수의 값으로 구해지며 이를 좀 더 자세히 살펴보면 다음과 같다.
먼저 모수가θ인 표본자료가 모집단f(x;θ)에서 취한 확률표본이라면 표본의 확률은 다음과 같은 우도함수 L(θ)로 나타낼 수 있다(Lee, 2018).
이때 Eq. (7)의 우도함수L(θ)의 최대값을 직접 구하는 것보다 우도함수L(θ)에 자연로그를 취하여 그 값을 최대화 시키는 모수값을 구하는 것이 훨씬 용이하다. 따라서 Eq. (7)의 양변에 자연로그를 취하면 Eq. (8)과 같게 되며 Eq. (8)을 최대로 하는 모수θ를 구하기 위해 Eq. (9)와 같이 일차 미분값을 취하고 0으로 하면 그 해가θ의 최우추정량이 된다. 즉 최우추정법(MLE)에 따른 최우추정량은 우도함수L(θ)를 극대화하는 모수θ값이 된다(Hogg and Tanis, 2005).
2.4 적합성 평가 척도
본 연구에서는 원전 전기화재 소방대 진압실패 확률모형 적합성 평가를 위해 Bayesian Information Criteria (BIC), Residual Sum of Square (RSS), Mean Squared Error (MSE)를 척도로 사용 하였다. 모형 적합도 평가를 위한 세 종류의 척도 모두 작은 값을 가질수록 우수한 모형 적합도를 나타낸다.
베이지안 정보기준 척도인 BIC는 확률변수의 수가 적을 경우에 모형 적합도 척도로서 우수한 성능을 보인다. 유사한 척도인 Akaike’s Information Criteria (AIC) 척도가 가지는 과대 적합 문제를 보완한 정보기준 척도로서 AIC에 비하여 모수의 수에 더 많은 벌점(Penalty)을 부여하여 단순한 모형을 선호하며 구하는 식은 Eq. (10)과 같다(Na, 2018).
여기서 n은 자료의 수, p는 모수의 수, yi는 i번째 관측값, (yi)은 확률모형을 통한 i번째 예측값을 나타낸다.
RSS는 잔차제곱합 즉 실제 관측값과 추정에 의한 예측값의 차이인 잔차(Residual) 혹은 오차(Error)의 제곱값의 합으로 이 값이 작을수록 모형 적합도가 좋으며 구하는 식은 Eq. (11)과 같다(Na, 2018).
여기서wi는 i번째 관측값에 대한 가중치를 나타낸다.
MSE는 평균제곱오차로서 가장 널리 사용되는 모형평가 척도중의 하나이며 구하는 식은 Eq. (12)와 같다(Kang et al., 2014).
3. 연구 방법 및 분석 자료
3.1 연구 방법
본 연구는 원전 화재사건 데이터를 활용하여 화재유발 점화원(Ignition Source) 중 화재 리스크에 가장 큰 기여를 하는 전기화재(NEI, 2010; Neville et al., 2017)를 대상으로 소방대에 의해 화재가 진압된 시간을 단일 확률변수로 선정한 후, 선행연구 결과를 기초로 선정된 32개의 연속형 확률분포를 화재진압시간 모형에 적합시켰다.
적합된 개별 확률모형에 대해 BIS, RSS, MSE 척도를 기준으로 모형 적합도 평가를 수행하여 가장 좋은 적합도를 보인 확률모형을 전기화재 최적 진압실패 확률모형으로 도출하고, 최우추정법(MLE)을 이용하여 관련 모수를 추정하였다.
추정된 최적 확률모형은 현행 화재 PRA에서 제안하고 있는 지수(Exponential) 확률모형과 적합도 척도들을 기준으로 비교 평가하여 성능 향상 정도를 확인하였다.
본 연구를 수행하기 위해 사용된 분석도구는 오픈소스(Open Source)로서 신뢰성분야, 빅데이터 분야, 딥러닝 분야, 데이터마이닝 분야, 인공지능 분야 등의 연구에서 활발히 사용되고 있는 R 프로그램(Song et al., 2018)을 사용하였다.
3.2 분석 자료
미국 NRC는 1968년부터 1989년까지 미국 원전에서 발생한 화재사건을 반영한 최신 화재 PRA 방법론인 NUREG/ CR-6850을 2005년에 발표한 후, 이후 발생한 2009년까지의 화재사건 데이터를 추가하여 기존 화재발생빈도와 소방대 화재진압실패 확률모형의 모수 값을 NUREG-2169를 통하여 개정하였다(NRC, 2015). 이에 본 연구에서는 NUREG- 2169에서 현행 화재 PRA의 최신 데이터 개정에 사용된 1968년부터 2009년까지 1,057건의 미국 원전 화재사건 데이터를 미국 NRC로 부터 확보하여 본 연구의 분석 데이터원으로 사용하였으며, 각 기간별 수집된 원(raw) 화재사건들의 데이터베이스 출처는 Table 2와 같다.
Table 2
Fire Event Data Source (NRC, 2015)
| Period | Data Source |
|---|---|
| 1968–1989 | ‧ LER* (component-level reporting rules) ‧ Additional data available: EN**s, NEIL***, NPRDS**** plant reports |
| 1990–1999 | ‧ LERs (significant event and system-level reporting rules) ‧ Additional data available: ENs, NEIL, NPRDS, plant reports |
| 2000–2009 | ‧ Systematic collection of plant- supplied reports and data records ‧ Supplemented with details from LERs and ENs |
수집된 1,057건의 화재사건은 현행 화재 PRA 방법론인 NUREG/CR-6850과 NUREG-2169에서 적용한 화재발생 원인 및 기기별 분류 기준과 동일한 기준을 적용하여 분류하였다.
특히, 분석대상인 전기화재는 전기캐비닛, 모터, 펌프, 옥내 변압기, 접속박스(Junction Box) 등에서 발생한 전기적 결함에 의한 화재를 포함 하였으며 , 동일한 전기적 결함에 의해 발생한 화재지만 주제어실(Main Control Room) 내 주제어반(Main Control Board), 옥외 대형 변압기, 터빈발전기 여자기(Excitor) 등에서 발생한 전기적 원인에 의한 화재는 화재 크기와 형상이 앞서 분류한 일반 전기캐비닛 등에서 발생한 화재와 달라 Table 1과 같이 별도로 분류하여 본 연구의 전기화재 소방대 진압실패 확률모형 도출 범위에서는 제외하였다.
또한, 이와 같이 분류된 전기 화재사건 중 진압시간에 대한 정보 확보가 가능한 화재사건만을 선별하여 최종적으로 총 177건의 화재사건을 분석대상 전기화재로 선정하였다.
Fig. 3은 원전에 설치된 전형적인 전기화재 유발 대상 기기들인 6.9 kv 스위치기어 전기 캐비닛, 펌프, 옥내 변압기, 주제어실 주제어반등의 예이다.
4. 연구 결과
4.1 원전 전기화재 소방대 진압시간 분석
4.1.1 소방대 진압시간 분석 결과
전기화재에 대한 소방대 진압시간의 기술통계(Descriptive Statistics) 분석 결과 소방대에 의해 화재가 진압되는데 걸린 시간은 평균 10.25분, 최소 0분에서 최대 95분까지 소요되었으며, 표준편차는 12.45분, 왜도(Skewness)는 3.05, 첨도(Kurtosis)는 13.37인 것으로 분석되었다(Table 3).
Table 3
Summary of Statistics for Electrical Fire Suppression Time
| Descriptive Statistics | Suppression Time (min) |
|---|---|
| Minimum | 0 |
| 1st Quartile | 2 |
| Median | 7 |
| Mean | 10.25 |
| 3rd Quartile | 13 |
| Maximum | 95 |
| Standard Deviation | 12.45 |
| Skewness | 3.05 |
| Kurtosis | 13.37 |
Table 3의 기술통계 결과 중 왜도(Skewness)와 첨도(Kurtosis)는 분포의 형태를 개략적으로 확인할 수 있는 척도들이다.
이 중 왜도(Skewness)는 Eq. (13)과 같이 평균에 대한 3차 적률(Moment)로 표현되는 비대칭의 척도로서 그 값이 양수이면 오른쪽으로 긴 꼬리를 가지는 형태의 분포 형태를 취하며, 음수이면 왼쪽으로 긴 꼬리를 가지는 분포 형태를 취한다. 정규분포처럼 완전 대칭인 경우 왜도(Skewness)는 0의 값을 가진다(Hogg and Tanis, 2005).
분석 대상인 원전 전기화재 소방대 진압시간 데이터의 왜도(Skewness)는 3.05로서 오른쪽으로 긴 꼬리, 즉 비대칭적으로 왼쪽으로 치우친 형태의 분포 모양임을 왜도(Skewness)값을 통하여 확인할 수 있다.
여기서σ는 표준편차, E는 기댓값, T는 화재진압시간 확률변수, u는 평균진압시간을 나타낸다.
첨도(Kurtosis)는 분포의 중앙부분의 뾰족함의 정도, 즉 분포가 중심 근처에 퍼져있는 정도에 대한 정보를 제공하는 통계량으로 정규분포의 첨도(Kurtosis)는 0의 값을 가진다. 첨도(Kurtosis)가 0보다 크면 정규분포 보다 중심부분이 더 뾰족하게 솟아 있는 긴 꼬리 형태를 가지는 모양의 분포 형태를 가지게 된다. 첨도(Kurtosis)는 Eq. (14)와 같이 평균에 대한 4차 적률(Moment) 값으로 표현된다(Huh and Song, 2013).
분석 대상인 원전 전기화재 소방대 진압시간 데이터의 첨도(Kurtosis)는 13.37로서 중심 근처에 뾰족한 형태의 분포 모양임을 첨도(Kurtosis)값을 통하여 확인할 수 있다.
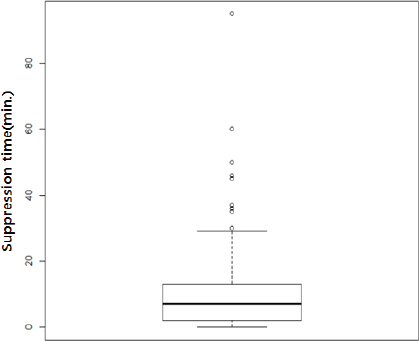
전기화재 진압시간에 대한 분위값(Quartile), 중앙값(Median), 최소값(Minimum) 및 최대값(Maximun)에 대한 흩어진 정도를 나타내는 Fig. 4의 상자그림(Box-plot)을 통해서도 진압시간이 작은 아래쪽에 중앙값(Median)을 중심으로 제1사분위수(1st Quartile)와 제3사분위수(3rd Quartile)내에 대부분의 값이 모여 있으며 진압시간이 큰 위쪽으로는 드문 형태의 분포를 하고 있음을 확인할 수 있다.
4.1.2 지수(Exponential) 확률모형 적합 및 한계
지수(Exponential) 확률분포는 음(Negative)이 아닌 시간 T에 대해 대부분 작은 값에 치우쳐져 있고 시간 T가 증가함에 따라 확률 밀도가 0에 근접하는 비대칭형 분포로서 왜도(Skewness)가 큰 분포 중에 하나이다(Lee et al., 2013).
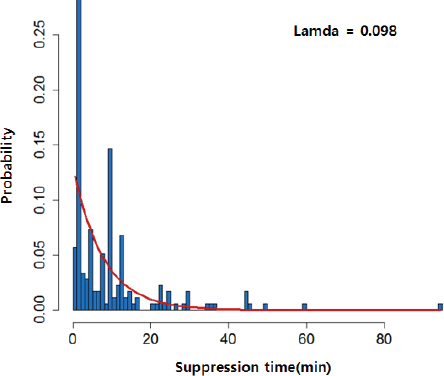
이와 같은 분포 특징을 가지고 있는 현행 원전 화재 PRA 방법론에서 제안하고 있는 Table 1의 전기화재에 대한 평균진압율 모수가 0.098인 지수(Exponential) 확률모형을 분석 대상 원전 전기화재 소방대 진압시간 모형에 적합 시킨 결과 Eq. (15)와 같은 소방대 진압 확률모형(f(t)) 및 Eq. (16)과 같은 소방대 진압실패 확률모형을 도출할 수 있다.
Fig. 5는 Eq. (15)의 지수(Exponential) 확률모형을 원(Raw) 자료에 적합시킨 결과를 도식화한 것으로 실제 데이터가 보여주는 시간 증가에 따른 진압확률이 증가와 감소를 보이는 봉우리 형태(청색 히스토그램)가 아닌 시간이 증가함에 따라 진압확률이 단조 감소하는 형태(적색 실선)로 적합 되어 실제 화재 경험 데이터를 대표하는 것에는 한계가 있음을 확인할 수 있다.
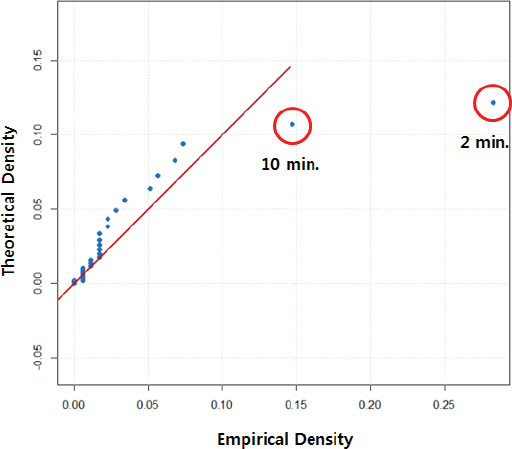
Eq. (15)의 지수(Exponential) 확률모형에 대한 적합성 검토를 위해 추가적으로, 모형의 적합성 정도를 주어진 데이터에 적합한 특정 확률모형에 얼마나 잘 따르는지를 분석하는데 유용한 시각화 도구인 Q-Q plot (Pandit and Infield, 2018)을 Fig. 6과 같이 도식화하였다.
그 결과, 진압시간이 30분 이상인 0에 가까운 확률을 가지는 시간대에 대해서는 적합시킨 지수(Exponential) 확률모형이 어느 정도 잘 적합하고 있으나, 발생 확률이 상대적으로 큰 초기 시간대 즉, 화재사건 경험에 따른 진압확률이 0.283인 구간(2분)과 화재사건 경험에 따른 진압확률이 0.147인 구간(10분)에 대해서는 실제 경험값에 비하여 지수(Exponential) 확률모형에서 추정한 값이 과소 추정되고 있음을 확인할 수 있다(Fig. 6).
4.2 소방대 진압실패 확률 모형
4.2.1 소방대 진압실패 확률모형 적합도 평가
확률모형 적합은 Leemis and Mcqueston (2008)가 미국 통계학회(American Statistical Association)에 발표한 57종의 연속형 단일 확률분포 중 R 프로그램(version 3.6.3)에서 구현이 가능한 32종의 확률 분포를 선정하여 원전 전기화재 최적 소방대 진압실패 확률모형 추정을 위해 적합시켰다.
Table 4는 소방대 진압실패 확률모형 도출을 위해 32개의 확률분포를 원전 전기화재 사건 모형에 적합시킨 결과로서 모형 적합도 평가 척도 중의 하나인 BIC를 기준으로 오름차순으로 정리한 것이다. 모형 적합도 평가를 위한 세 가지 척도 중 RSS는 상대적으로 다소 큰 값을 나타내지만 나머지 두 척도인 BIC와 MSE는 가장 작은 값을 가지는 3-Parameter Weibull 확률모형을 최적 확률모형으로 선정하였다.
Table 4
Probability Distributions Applied to Electrical Fire Suppression Time
4.2.2 최적 소방대 진압실패 확률모형
소방대 진압실패 확률모형 적합 및 적합성 평가 결과 3-Parameter Weibull 확률모형이 원전 전기 화재 소방대 진압시간에 따른 진압 실패 경험 데이터를 가장 잘 대표하는 최적 확률모형으로 도출되었다.
3-Parameter Weibull 확률모형은 Eq. (17)과 같이 위치(Location), 형상(Shape), 척도(Scale) 3개의 모수를 필요로 하는 Weibull 확률모형의 일종으로 최근 피로수명분포, 인공위성 신뢰도 연구분야 등에서 활용도가 높이 평가되어 그 가치를 인정받고 있는 확률모형이다(Cousineau, 2009). 특히 3-Parameter Weibull 확률모형은 증가 및 감소를 보이는 왜도(Skewness)가 심한 봉우리 형태를 보이는 서로 다른 종류의 시스템 고장률 적합에 유용한 것으로 알려져 있으며(Moeini et al., 2013), 3-Parameter Weibull 소방대 진압실패 확률모형은 Eq. (18)과 같다.
여기서α는 위치모수, γ는 형상모수, β는 척도모수를 나타낸다.
도출된 3-Parameter Weibull 확률모형의 위치(Location), 형상(Shape), 척도(Scale) 모수를 최우추정법(MLE)을 이용하여 추정한 결과, 위치(Location) 모수는 1.5, 형상(Shape) 모수는 0.914, 척도(Scale) 모수는 20.047로 각각 추정되었다(Table 5).
Table 5
MLE for 3-Parameter Weibull Distribution
| Parameters | MLE (Maximum Likelihood Estimate) |
|---|---|
| Location (α) | 1.5 |
| Shape (γ) | 0.914 |
| Scale (β) | 20.047 |
Fig. 7은 Table 5에서 추정된 3-Parameter Weibull 확률모형에 대한 최우추정치(MLE) 모수들을 Eq. (17)에 적용하여 원(Raw) 자료에 적합(Fitting)한 결과를 도식화한 것으로, 실제 관측 데이터가 보여주는 시간 증가에 따른 진압확률의 증가와 감소 형태(청색 히스토그램)의 분포를 3-Parameter Weibull 확률모형(적색 실선)이 10분 구간에서의 진압확률 증가 부분을 제외하고 초기 2분 구간에서의 진압확률의 증가와 감소를 잘 대표하며, 현행 화재 PRA 방법론에서 제안하고 있는 지수(Exponential) 확률모형에 비해 실제 화재 경험 데이터를 잘 적합시키고 있음을 알 수 있다.
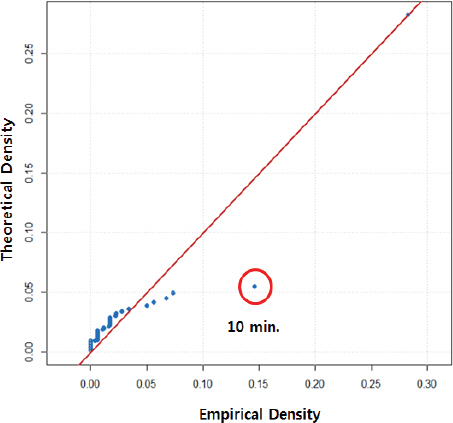
Eq. (17)의 3-Parameter Weibull 확률모형에 대한 적합성 검토를 위해 Q-Q plot을 Fig. 8과 같이 도식화한 결과, 화재사건 경험에 따른 진압확률이 0.147인 구간(10분)에서 실제 경험값에 비하여 3-Parameter Weibull 확률모형을 통해 추정된 값이 과소 추정된 것을 제외하고 전반적으로 잘 적합하고 있음을 확인할 수 있다.
4.3 결과 및 논의
최우추정법(MLE)를 이용하여 177건의 원전 전기화재 사건에 대한 소방대 진압실패 확률모형을 추정한 결과 Eq. (19)와 같은 3-Parameter Weibull 진압실패 확률모형이 최적 모형으로 도출되었다.
현행 화재 PRA 방법론에서 제안하고 있는 지수(Exponential) 확률모형과 도출된 3-Parameter Weibull 확률모형의 모형 적합도 척도를 비교한 결과, 3-Parameter Weibull 확률모형이 BIC는 17.7%, RSS는 24.4%, MSE는 58.2% 감소하여 모형 설명력이 증가하였음을 확인하였다(Table 6).
Table 6
Result of Comparison for Model Adequacy Criteria
| Criteria | Distribution | ||
|---|---|---|---|
| Exponential | 3P Weibull | Decrease Rate | |
| BIC | -416.9579 | -490.8581 | 17.7% |
| RSS | 4.22E-03 | 3.19E-03 | 24.4% |
| MSE | 6.60E-04 | 2.76E-04 | 58.2% |
그러나 이와 같이 3-Parameter Weibull 확률모형이 지수(Exponential) 확률모형 보다 설명력이 향상되고 우수한 적합도를 보이며 Fig. 6의 지수(Exponential) 확률모형에서의 과소 추정 문제가 일부 개선된 적합을 보이고 있으나, Fig. 8과 같이 실제 화재사건 경험에 따른 진압확률이 0.147인 구간(10분)에서는 지수(Exponential) 확률모형과 동일하게 과소 추정하는 경향이 존재하고 있어 일부 구간에서의 과소 추정에 대해서는 여전히 개선되지 못한 구조를 가지고 있는 한계가 있음을 확인하였다. 이러한 3-Parameter Weibull 확률모형이 보이고 있는 한계는 3-Parameter Weibull 확률모형 뿐만 아니라 지수(Exponential) 확률모형에서도 동일하게 나타나는 한계로서 이는 단일 확률모형이 가지는 고유의 구조적 특성에 따른 것으로 판단된다.
5. 결 론
본 연구는 원전 리스크 정보 성능기반(RIPB) 화재방호 프로그램 적용 등에서 화재 PRA 분석결과의 신뢰성 확보 및 향상을 위해 원전 화재 리스크 기여도가 큰 전기화재를 중심으로 실제 화재 특성이 반영된 최적 소방대 진압실패 확률모형을 도출하고 해당 확률 모형의 모수를 최우추정법(MLE)을 이용하여 추정하였다.
최적 전기화재 소방대 진압실패 확률모형 도출을 위해 현행 화재 PRA 방법론인 NUREG/CR-6850에서 제시하고 있는 화재발생빈도와 소방대 화재진압실패 지수(Exponential) 확률모형의 모수 값 개정을 위해 NUREG-2169에서 적용한 1968년부터 2009년까지의 미국 원전 화재사건 데이터를 활용하여, 미국 통계학회(ASA)에서 발표한 32개의 연속형 확률분포를 NUREG/CR-6850 및 NUREG-2169와 동일한 분류 기준으로 선정한 177건의 전기 화재사건에 적합 시킨 후 모형 적합도를 평가하였다. 평가 결과, 모형 적합도 척도인 BIC는 –490.8581, RSS는 3.19E-03, MSE는 2.76E-04로 평가된 3-Parameter Weibull 확률모형이 최적 소방대 진압실패 확률모형으로 도출되었다.
도출된 3-Parameter Weibull 확률모형의 모수(Parameter)들인 위치(Location) 모수, 형상(Shape) 모수, 척도(Scale) 모수는 최우추정법(MLE)을 이용하여 각각 1.5, 0.914, 20.047로 추정되었다.
이와 같이 추정된 3-Parameter Weibull 확률모형은 현행 화재 PRA 방법론에서 제안하고 있는 지수(Exponential) 확률모형과 모형 적합정도를 비교하였으며, 그 결과 모형적합도 척도인 BIC는 17.7%, RSS는 24.4%, MSE는 58.2% 감소하여 모형 설명력이 향상되었음을 확인하였다.
그러나 실제 화재 특성이 반영된 최적 소방대 진압실패 확률모형으로 도출된 3-Parameter Weibull 확률모형은 화재사건 경험에 따른 진압확률이 0.147인 구간(10분)에서 실제 경험값에 비하여 3-Parameter Weibull 확률모형을 통해 추정된 값이 과소 추정되는 한계가 있음을 확인할 수 있었다. 이는 3-Parameter Weibull 확률모형 뿐만 아니라 지수(Exponential) 확률모형에서도 동일하게 나타난 한계로서 단일 확률분포 고유 특성에 따른 것으로 판단된다.
이러한 한계에도 불구하고 본 연구를 통하여 도출된 3-Parameter Weibull 확률모형은 현재 알려져 있는 연속형 확률분포중 소방대 진압실패모형에 가장 적합도가 우수한 확률모형으로서, 현행 화재 PRA 방법론에서 제안하고 있는 지수(Exponential) 확률모형 보다 모형 적합도가 증가되어 실제 화재 경험에 대한 설명력이 더욱 향상된 확률모형으로 정량적 원전 화재 리스크 평가 기법인 화재 PRA의 분석 현실성(Realism) 확보 및 향상에 더욱 기여할 수 있을 것이다.