2.1 지배방정식

본 연구에서 적용한 Godunov형 유한체적모형은 2차원 천수방정식을 지배방정식으로 하며, Eq. (1)과 같이 지배방정식을 벡터형태로 나타낼 수 있다.

여기서, U는 보존변수들로 이루어진 물리적 벡터, 그리고 F(U) 및 G(U)는 각각 x와 y방향의 흐름율(Flux), S(U)는 하상경사 및 마찰경사항 그리고 Q(U)는 생성/소멸항이다. Q(U)항은 흐름 및 홍수해석에서 강우, 맨홀의 월류량, 보(Weir)의 지형을 고려하지 않은 유출량 등을 고려할 수 있다.

u와 v는 각각 x와 y 방향의 속도, g는 중력가속도, h는 수심, S₀는 하상경사로 x 및 y 방향에 대해 각각 S_0x = -∂z_b/∂x, S_0y = -∂z_b/∂y로 표현되며, S_fx와 S_fy는 각각 x 및 y 방향의 마찰경사이다.

2.2 체적-수위 관계(Volume-Free surface Relationships, VFRs)

유한체적기법은 격자내 유체체적을 계산하기 위한 지표로 격자 중심에서의 평균수심을 적용한다. 하지만, 부분적으로침수된 격자의 경우는 격자중심에서의 수심이 평균수심을 대표하기에는 어려울 수도 있다. 예를 들어, 격자내의 자유수면이 격자 중심표고(z_c)보다 낮은 경우 실제 격자 내에는 물이 있음에도 불구하고 물이 없는 마른격자로 간주되어질 수 있다. 홍수해석시 격자의 부분 젖음으로 발생할 수 있는 이러한 문제점을 해결하기 위해, VFRs에서는 격자 중심에서의 수위와 수심을 구분하였다. 각 격자에서의 수심(h)은 유체의 체적(V)와 면적(Λ)의 비로 정의하는 반면, 수위(η)는 격자내의 젖은부분에서의 자유수면으로 정의한다. 완전 젖음 격자에서는 수위=수심+격자 중심표고(η=h+z_c)가 성립하지만, 부분 젖음 격자에서는 이 등식은 성립하지 않는다. 이러한 경우에는 VFRs를 이용하여 수위와 수심사이의 관계가 결정되도록 하였다. 절점의 표고가 각각 z₁, z₂, z₃, z₄(z₁<z₂<z₃<z₄)인 VFRs는 다음과 같이 표현할 수 있다(Kim et al., 2014).

여기서 h¯2, h¯3, h¯4는 각각 격자를 구성하고 있는 절점 z₂, z₃ 및 z₄의 높이까지 채워진 물에 해당하는 물 저장 매개변수를 나타낸다.

Eq. (1)은 삼각 혹은 사각격자(N_m)와 격자를 구성하고 있거나 둘러싸고 있는 절점(N_n)과 선분(N_l)에 대해 이산화된다(Fig. 1). 각 격자의 절점에는 대상유역에서 절점의 위치에 해당하는 지형고가 물려 있으며, 격자내의 지형고는 두 절점을 연결하는 선분을 따라 선형보간 된다. 두 절점을 연결하면 하나의 선분이 생성되고, 세 절점을 연결하면 하나의 면이 구성된다. 즉 세 개의 절점으로 이루어진 삼각격자의 경우는 지형이 하나의 평면으로 모델링된다. 반면, 네 개의 절점으로 이루어진 사각격자의 경우는 대각선으로 양분된 두 개의 삼각격자로 나누어 질수 있어 두 개의 평면으로 지형이 모델링되므로 삼각격자보다는 지형처리가 복잡하게 된다.

Fig. 1

Composition of Mesh

삼각격자에서의 VFRs는 단지 세 개의 절점 높이(z₁, z₂, z₃)와 두 개의 물 저장 매개변수(h¯2, h¯3)로만 이루어진다. Begnudelli and Sanders (2006)는 삼각격자에서의 물의 저장은 절점의 높이 z =(z₁, z₂, z₃; z₁≤z₂≤z₃)와 η의 함수인 h_T로 계산하였으며, 다음 식과 같이 나타내었다.

삼각격자의 경우, 물 저장 매개변수의 계산(h¯i)은 Eq. (5)와 같이 간단하게 계산할 수 있다.

앞서 언급하였듯이, 사각격자의 경우는 두 개의 삼각격자로 나누어서 계산이 이루어지므로 그 계산과정이 조금 더 복잡하다. 사각격자를 두 개의 삼각격자로 나누고(나누어진 2개의 삼각격자는 각각 a와 b), 각 삼각격자의 절점표고를 z_a와 z_b라 하면, 나누어진 각 삼각격자의 총 저장용량을 계산은 Eq. (4)를 적용하여 이루어진다. Begnudelli and Sanders (2007)은 z_a와 z_b에 대해 다음과 같이 사각격자를 3가지 방법으로 나누는 방법을 제안하였으며, 3가지 방법에 대한 모식도는 Begnudelli and Sanders (2007)에서 보여준다.

(1) 가장 낮은 절점(z₁)과 높은 절점(z₄)이 대각으로 반대편에 위치한 경우,

(2) 가장 낮은 절점(z₁)과 높은 절점(z₄)이 동일한 면에 위치하고, z₁과 z₂이 다른 면에 위치하는 경우,

(3) 가장 낮은 절점(z₁)과 높은 절점(z₄)이 동일한 면에 위치하고, z₁과 z₃가 다른 면에 위치하는 경우이며, 이 경우는 가장 표고가 높은 두 개의 절점이 대각으로 마주보며 위치하고 가장 표가가 낮은 두 개의 절점이 대각으로 마주보며 위치한다.

사각격자를 위에서 구분한 3가지 경우 중 하나로 나눈 후, 물 저장 매개 변수는 다음과 같이 두 삼각격자의 면적 가중 평균으로 계산된다.

여기서 Λ_a와 Λ_b는 각각 사각격자에서 두 개로 나누어진 삼각격자 a와 b의 평면적을 나타낸다. 앞서 언급하였듯이, 수심 자체가 보존되는 속성이지 않으므로, 체적을 보존하기 위해서 면적가중을 적용하였다. 물 저장 매개 변수는 모형의 전처리 단계에서 계산되므로 보존변수들의 업데이트가 이루어지는 예측단계(Predictor step) 및 수정단계(Corrector step)에서 이 작업은 선형보간으로만 제한된다. 중요한 것은 η, h, z가 최저표고 절점에서 최고표고 절점까지 단조 증가하므로 VFRs 기법은 선형보간으로 전방향(h로부터 η 계산) 혹은 후방향(η로부터 h 계산)으로 적용 될 수 있다.

3.1 단면 확대/축소 구간이 존재하는 실험하도

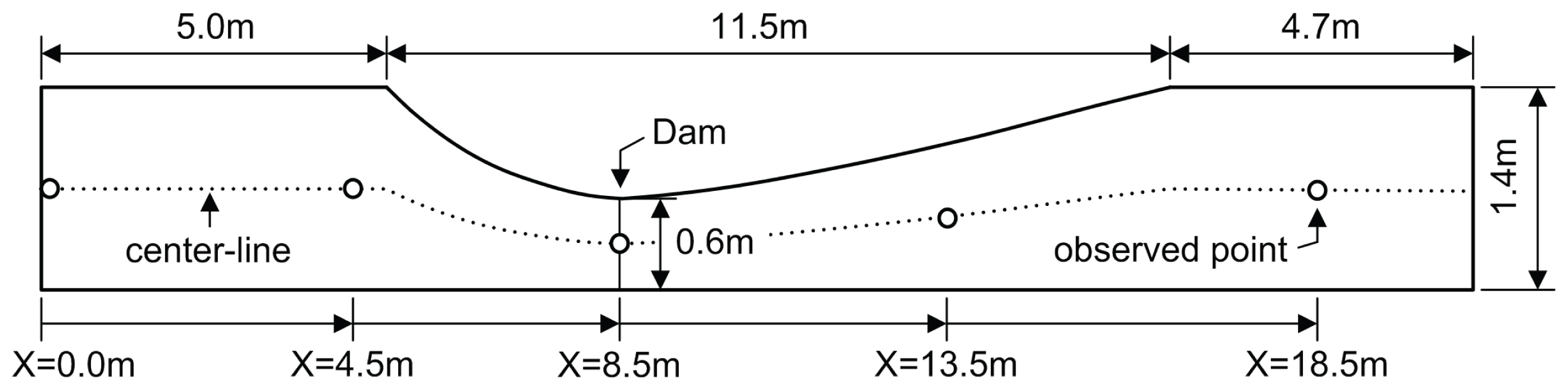
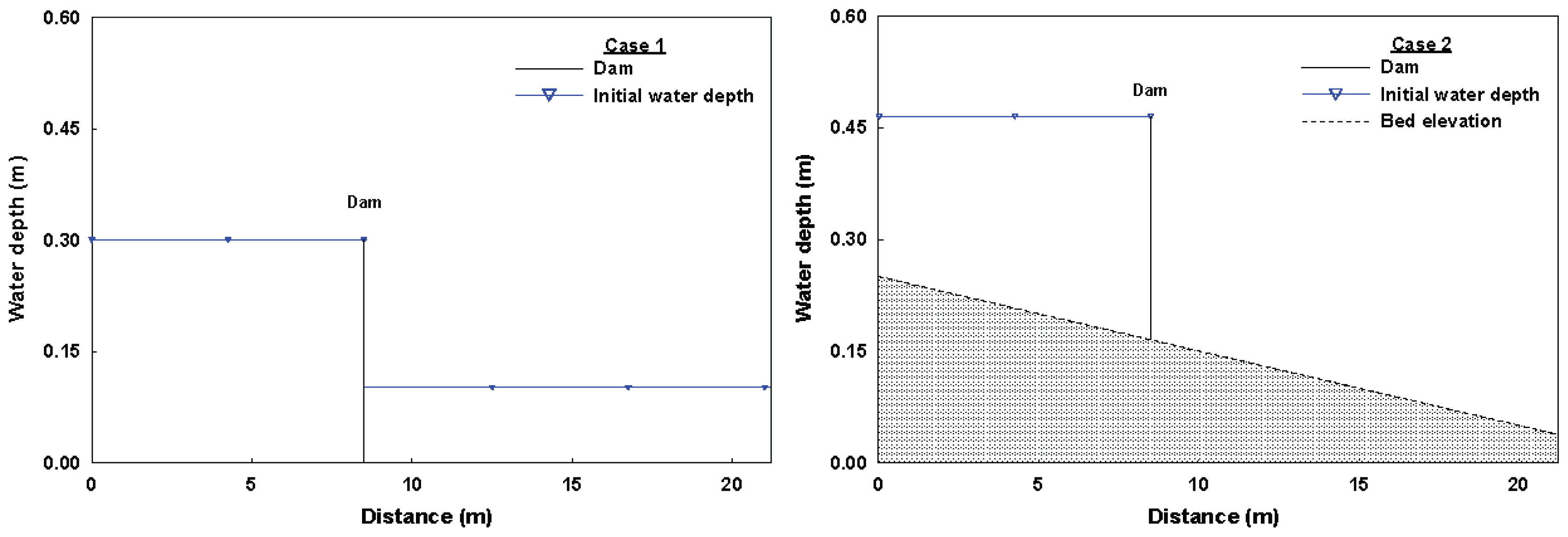
Bellos et al. (1992)는 폭이 축소, 확대되는 실험하도를 대상으로 다양한 초기조건 및 하상경사에 따른 댐 붕괴 흐름 실험을 수행하였다. 실험하도는 길이 21.2 m, 폭은 1.4 m에서 0.6 m까지 변하며, 댐은 상류단으로부터 8.5 m 지점인 폭이 가장 좁은 부분에 위치하고 있다(Fig. 2). 본 연구에서는 Bellos et al. (1992)이 수행한 여러가지 실험조건 중에서 댐 하류단이 마른 경우와 젖은 경우의 2가지 댐 붕괴 조건에 대해 모형을 검증하였다. 2가지 경우에 대한 모의 조건은 Table 1에서 보여주며, 초기조건은 Fig. 3에 나타내었다. Case 1은 하상경사가 없고 저수지의 초기수심 0.30 m, 댐 하류단의 초기수심은 0.101 m인 젖은하도 조건이다. 하상의 조도는 실험하도의 재질(Glass-steel)과 가까운 근사인 0.012 m^-1/3s(Soulis, 1992), 하류단 경계조건은 연속적인 흐름을 가정하여 보(Weir) 조건을 적용하였다. Case 2는 하상경사가 0.01(최상류단 높이가 0.25 m, 최하류단 높이 0.038 m, Fig. 3), 저수지 초기수심은 0.215 m(초기수위는 0.465 m), 댐 하류단의 초기수심은 0.0 m인 마른하도 조건이다. 하상의 조도는 Darcy-Weisbach 식이 적용되었으며, 하류단 경계조건으로 열린(Transmissive) 조건을 지정하였다. 2가지 경우 모두 상류단에는 댐 내로 유입되는 유량이 없는 닫힌(Solid) 조건, 모의시간은 댐 붕괴 후 70초로 지정하였다. 모의결과를 5개의 관측지점(x= 0.0, 4.5, 8.5, 13.5, 18.5m)에서의 실측자료와 비교하였다(Fig. 2).

Fig. 2

Layout of Non-prismatic Channel Dam-break

Table 1

Test Condition for Non-prismatic Channel Dam-break

Fig. 3

Initial Condition of Non-prismatic Channel Dam-break

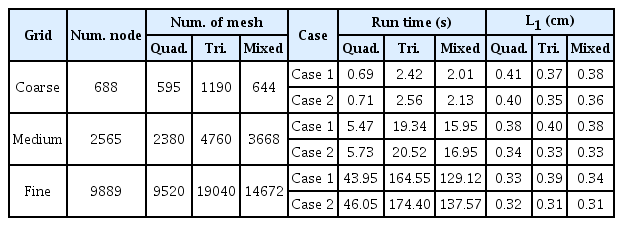
격자형상에 따른 VFRs의 적용성 및 정확성을 검증하기 위해, 삼각, 사각 그리고 혼합격자를 구성하였다(Fig. 4). 또한 구성한 격자의 해상도에 따른 적용성을 검증하기 위해 Table 2에서 보여주는 것과 같이 각 격자별 3가지 해상도에 대해서도 격자를 생성하였다. 먼저, 사각격자의 해상도는 ∆x=0.25 m, ∆y는 폭이 변하지 않는 부분에서는 0.20 m, 폭이 변하는 부분에 대해서는 일정하지 않은 해상도(0.0857∼0.1871 m)로 생성하였다. 삼각격자는 각 사각격자에서 대각으로 위치한 두 개의 절점을 연결하여 2개의 삼각격자를 생성하였다. 혼합격자는 하도의 폭이 변하는 구간(5∼16.5 m)에서는 삼각격자로, 나머지 부분은 사각격자로 구성하였다(Fig. 4). 그리고 각 격자형상별 구성된 기본격자를 기본으로 1/2(∆x*∆y), 1/4(∆x*∆y)의 더 정밀한 해상도를 가진 중간(Medium), 조밀(Fine) 격자를 추가적으로 생성하였다. 이러한 방법으로 구성된 격자에 대한 총 절점과 격자의 수는 Table 2에 나타내었다.

Fig. 4

2D Mesh for Non-prismatic Channel (a) Quadrilateral, (b) Triangular and (c) Mixed mesh

Table 2

Mesh Property, Run Time and L₁ for Non-prismatic Channel Dam-break

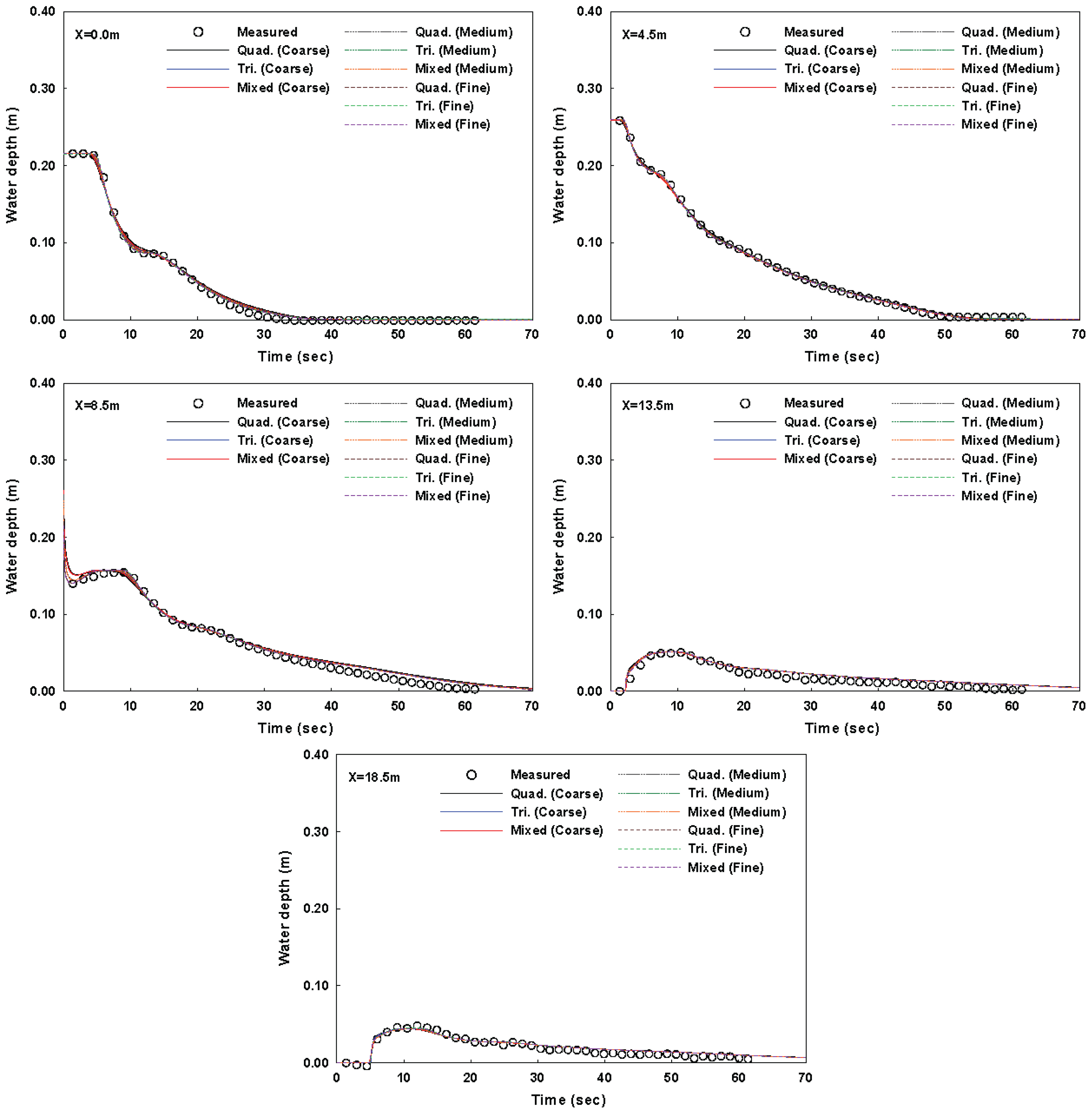
Figs. 5와 6은 각각 Case 1과 Case 2에 대해 3가지 격자유형을 적용하여 계산된 수심과 5개의 관측지점에서 실측된 수심과의 비교를 보여준다. 3가지 격자유형 모두 댐붕괴파가 하류의 젖은하도(Case 1) 및 마른하도(Case 2)로 전파하는 동안 하도의 수축/확대 영향을 잘 반영하여 모의하였다. Case 1에서는 댐붕괴로 인해 하류로 전파된 홍수파 및 하류단 초기수심을 유지하기 위해 최하류단에서 고려한 위어의 영향으로 인한 상류방향 반사파의 수심 및 도달시간이 비교적 잘 일치하였다. 또한, Case 2에서도 경사가 있는 마른하도에서 홍수심 및 홍수파 전파시간도 잘 예측하였다.

Fig. 5

Prediction and Measurement of Water Depth for Case 1 of Non-prismatic Channel

Fig. 6

Prediction and Measurement of Water Depth for Case 2 of Non-prismatic Channel

격자유형과 해상도에 따른 모형 수행능력의 정량적인 평가를 위해, 모의에 소요되는 계산시간(Run time), 5개의 관측지점(Fig. 2)에서의 실측값과 모형의 계산값과의 L₁오차를 산정하여 Table 2에 나타내었다. 계산시간은 모의상황에 따라 변동이 생길 수 있으므로 가능한 동일조건을 유지하고 모의를 5회 반복하여 측정한 시간을 평균하여 산정하였다. 오차 산정을 위해 사용한 L₁ 식은 Eq. (10)에 나타내었다.

여기서, N_m은 격자의 수, h_m과 N_c는 각각 계산격자 j에서의 실측 및 계산수심을 의미한다.

Table 2에서 보여주듯이, 젖은/마른 하도에 따른 계산시간은 경사가 없는 젖은하도(Case 1)에서의 사각, 삼각 그리고 혼합격자는 경사가 있는 마른하도(Case 2)보다 기본격자(Course)에서는 각각 평균 3.0%, 5.8%, 6.0%, 중간격자(Medium)에서는 각각 평균 4.8%, 6.1%, 6.8%, 조밀격자(Fine)에서는 각각 4.8%, 6.0%, 6.5% 더 빠르게 계산이 이루어져 격자해상도에 관계없이 유사한 결과를 보여주었다. 격자의 유형에 따른 계산시간은 3가지 유형의 격자 중에서 사각격자가 가장 빠른 속도를 보여주었으며, 기본해상도에서 사각격자는 삼각 및 혼합격자보다 평균(Case 1과 Case 2) 256%, 196%, 중간해상도에서는 256%, 194%, 조밀해상도에서는 277%, 196% 빠른 계산시간이 산정되어 격자의 해상도와 관계없이 유사한 계산시간 비율을 보여주었다. L₁ 산정에서는 3가지 격자 모두 Case 2가 Case 1보다 조금 더 작은 오차를 보여주었으며, 평균적으로 Case 1에서는 사각, 혼합, 삼각격자의 순서로, Case 2에서는 삼각, 혼합, 사각격자의 순서로 작은 오차가 산정되었다. 부분마름/젖음을 포함하는 마름/젖음이 확연하게 발생하는 실험하도에 격자의 유형 및 해상도를 다르게 하여 산정된 모형의 계산시간 및 L₁오차는 모두 합리적인 값을 보여주어 본 연구에서 적용한 VFRs가 격자의 종류 및 크기에 관계없이 모두 잘 적용되고 있음을 확인할 수 있었다.

3.2 Malpasset 댐 붕괴

실제지형에 대한 VFRs의 적용성 검증을 위해 현장조사 및 실험자료가 존재하는 Malpasset 댐 붕괴 경우를 모형에 적용하였다. Malpasset 댐은 프랑스 남동쪽에 위치한 도시인 Fréjus에서 약 12 km 상류지점의 Reyran 강의 계곡 부분에 폭 1.5∼6.77 m, 높이 66.5 m, 길이 223m, 저수용량 55×106 m³으로 1954년 건설되었다. 하지만 1959년 12월 2일부터 10일 동안 Reyran 강 유역에 내린 500 mm 이상의 강우로 인해 댐은 붕괴되었고, 40 m이상의 높은 홍수파 일으키며 하류로 전파되어 계곡의 지형을 급격히 변화시키고, 421명의 사망자를 발생하게 하였다(Valiani et al., 2002).

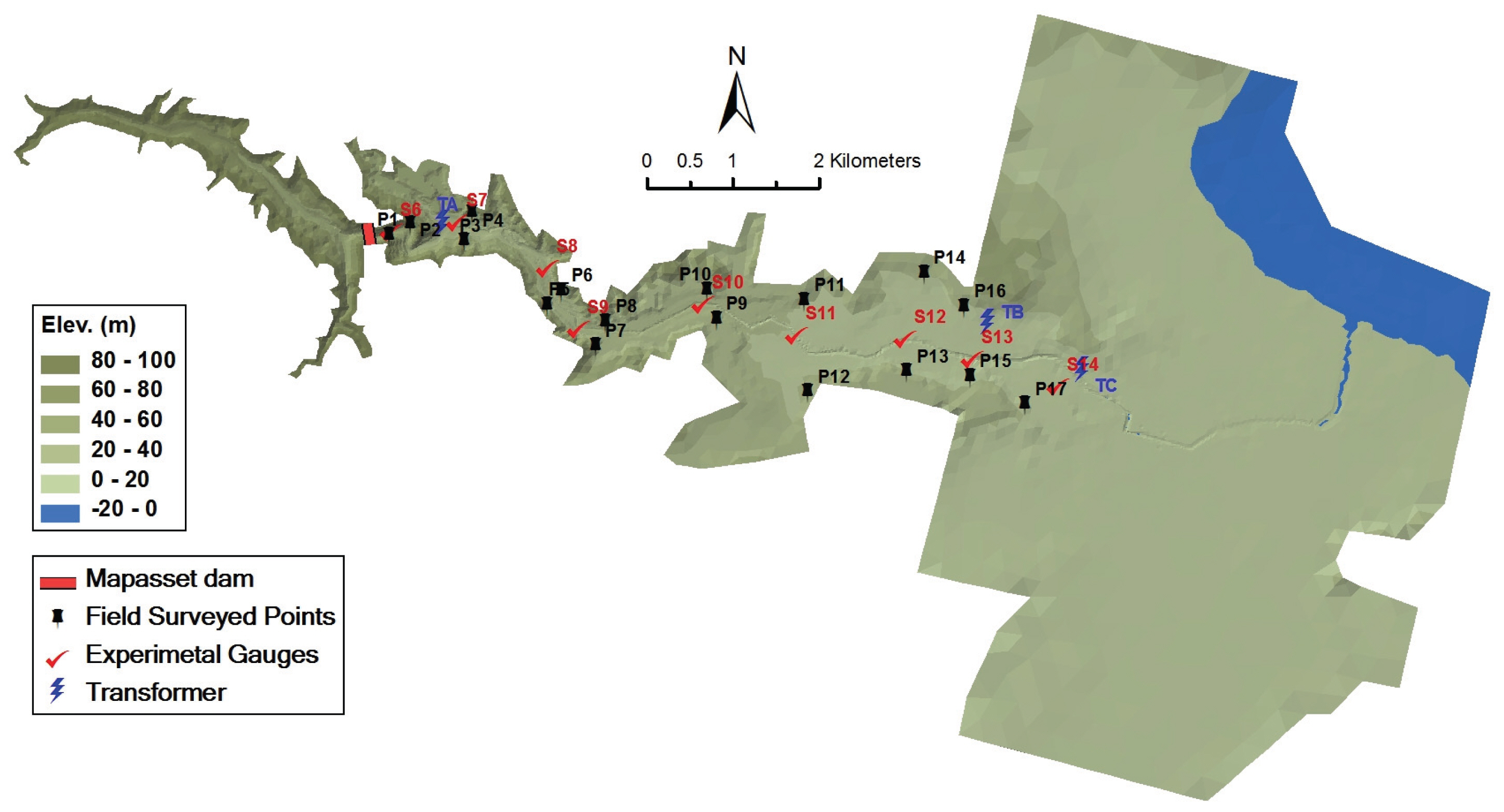
댐 붕괴로 인해 하류로 전파된 홍수파의 최고수위는 댐 붕괴 후 경찰에 의해 Reyran 강의 좌·우 제방에 남아 있는 흔적수위로 조사되었으며, 홍수파의 전파시간은 댐 하류에 위치한 3개의 전신주의 정전시간으로 유추되었다(Valiani, et al., 2002). Fig. 7에서 P1∼P17은 흔적수위가 경찰에 의해 현장조사된 지점들을 나타내며 A, B, C는 3개 전신주의 위치를 보여준다. 1964년에는 프랑스 전력 국립수리실험실(EDF-LNH)에서 1:400 규모로 실험실 모형을 제작하여 Malpasset 댐 붕괴에 대한 재현 실험을 수행하였다. 이 물리모형을 이용한 실험 수행을 통해 댐 하류 9개의 지점에 대해 최고 홍수위와 홍수파 도달시간을 측정하였으며, 측정된 지점은 Fig. 7에서 S6∼S14으로 보여준다. 경찰에 의해 현장조사된 홍수흔적, 3개 전신주의 정전시간, 실험실에서 재현된 물리모형의 게이지로 측정된 최고 홍수위 및 홍수파 도달시간을 모형의 검증을 위해 사용하였다.

Fig. 7

Topography and Locations of Field Surveyed Points and Laboratory Gauges

EDF-LNH에서는 Malpasset 댐의 저수지 및 하류부 지형을 댐 붕괴 이전에 구축된 자료(1/20,000 IGN map of Saint-Tropez n°3, dated 1931)를 바탕으로 13,541개의 점(Point) 표고를 추출하였으며(Goutal et al., 1999), 이 자료는 연구유역에 대해 –20∼+100 m의 표고로 표출되며 대략 ±50 cm의 수직오차를 가진다(Goutal, 1999; Valiani et al., 2002; Dewals et al., 2006). 본 연구에서는 이 지형자료를 바탕으로 ArcGIS 10을 이용하여 TIN(Triangulated Irregular Network) DTM (Digital Terrain Model)을 구축하였다(Fig. 7).

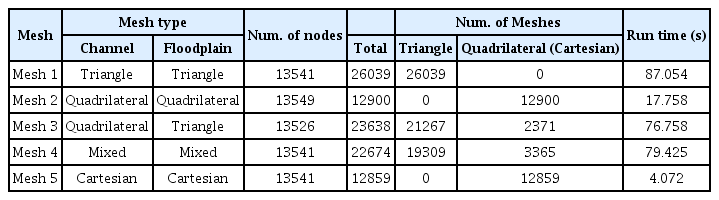
Fig. 8은 Malpasset 댐 붕괴에 대한 2차원 수치모의를 위해 생성한 5가지의 격자 유형을 보여준다. 격자생성을 위해서는 SMS 10.1(Aquaveo, Provo, UT)과 Triangle(Shewchuk, 1996)이 이용되었으며, 생성된 격자들은 격자 형태별 VFRs의 적용성 및 정확성을 검증하기 위해 사용되었다. Mesh 1, Mesh 2 그리고 Mesh 5는 각각 하도와 홍수터 포함하는 계산영역에 대해 삼각, 사각 그리고 정방형 격자로 구성하였다. Mesh 3은 하도에 대해서는 사각격자, 홍수터에 대해서는 삼각격자로 구성하였으며, Mesh 4는 전체 계산영역에 대해 삼각과 사각격자가 혼용된 혼합격자로 구성하였다. 특히, Mesh 1과 Mesh 4는 EDF-LNH에서 디지타이즈(Digitize)한 13,541개의 점에 대해 어떠한 위치 변경 없이 각 격자의 절점으로 구성되도록 격자를 생성하였다. 일반적으로 복잡한 실제 지형을 대상으로 한 2차원 수치모의에서 계산영역에 대해 사각격자로만 구성하는 작업은 많은 노력과 시간이 필요하다. 본 연구에서도 전체 계산영역에 대해 사각격자로만 구성한 Mesh 2를 수작업으로 생성하기 위해 많은 시간과 노력을 소요하였다. Mesh 3은 하도에 대해 수작업으로 사각격자를 생성하였으며, 홍수터에 대해서는 Mesh 1과 Mesh 4와 같이 EDF-LNH에서 디지타이즈한 13,541개의 점 자료를 이용하였다. Mesh 5는 다른 격자의 절점 수와 동일한 절점 개수를 생성하기 위해 61.84 m 해상도로 정방형 격자를 생성하였다. 각 격자에 지형고를 반영하기 위해, 13,541개의 점 자료로 생성된 TIN으로부터 각 격자의 절점에 실제 지형이 할당되도록 하였다. 각 격자에 사용된 격자와 절점의 수는 Table 3에서 보여준다.

Fig. 8

Considered Meshes for Malpasset Dam-break Case; (a) Triangular mesh, (b) Quadrilateral mesh, (c) Mixed mesh with quadrilaterals along the river and triangles everywhere else, (d) Mixes triangles and quadrilaterals everywhere, and (e) Cartesian grid

Table 3

Mesh Property and Model Run Time for Malpassent Dam-break

저수지의 초기수위는 100 m, Reyran 강의 초기유량은 댐 붕괴유량에 비해 무시할 정도로 적으므로 마른 하도로 고려하였으며(Valiani et al., 2002), 댐이 붕괴되면 저수지의 100 m 수위에 해당하는 유량이 댐 하류부의 마른 하도 및 홍수터로 흘러내려가도록 하였다. 상류단 경계조건으로는 댐 붕괴가 발생하는 동안 저수지내 유입 유량은 댐 붕괴유량에 비하면 매우 적으므로 저수지 유입이 없는 닫힌 경계조건을 적용하였다. 하류단 경계조건은 댐 붕괴 당시 조위에 대한 상세한 자료 및 정보가 없어 조위조건 대신 댐 유량이 바다로 흘러들어갈 수 있는 열린 경계조건을 적용하였다(Valiani et al., 2002; Yoon and Kang, 2004). 연구유역을 대상으로 한 조도(Roughness) 민감도에 대한 연구는 다른 연구자들(Hervouet and Petitjean, 1999; Dewals et al., 2006; Franchello and Krausmann, 2008; Li and Duffy, 2011)에 의해 많이 수행되었으며, 본 연구에서는 n_m=0.033 m^-1/3s을 적용한 기존의 연구(Valiani et al., 2002; Brufau et al., 2004; Yoon and Kang, 2004; Liang et al., 2007; Singh et al., 2011)와 동일하게 적용하였다. 전체 모의시간은 댐 붕괴 후 3600 ^-1/3s로 하였다.

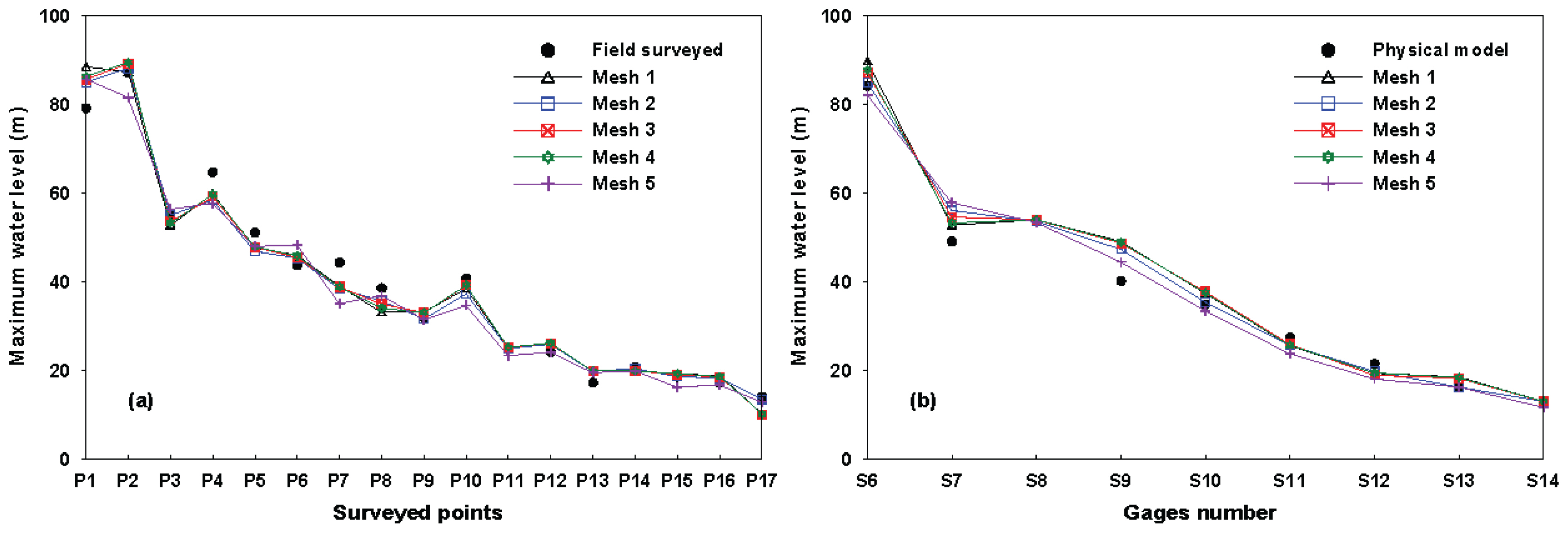
Fig. 9(a)는 현장의 우측 및 좌측 제방에 남아있던 홍수흔적으로 조사된 최고수위와 각 격자를 이용해 계산된 수위와의 비교를 보여준다. Fig. 9(b)는 EDF-LNH의 실험 모형에서 측정한 최고 홍수위와 계산수위와의 비교를 보여준다. VFRs를 적용한 각 격자에 대한 모의 소요시간(Run time)을 산정하여 Table 3에 나타내었으며, 동시에 각 격자에서 예측된 홍수위에 대한 정확도의 정량적 평가를 위해 L₁ 오차를 산정하여 Table 4에 나타내었다. 모의 소요시간은 격자별 구성된 격자의 수에 따라 차이를 보였지만, 다른 연구들(Valiani et al., 2002; Yoon and Kang, 2004)의 모의시간과 비교해보면 모두 합리적인 범위 안에 있는 것으로 판단되었다. 현장 조사된 홍수흔적 최고수위와 실험모형의 측정 최고 수위를 동시에 고려하여 계산된 L₁ 오차에서의 정확도는 Mesh 2, Mesh 3, Mesh 4, Mesh 1 그리고 Mesh 5 순이었다. 모의 소요시간은 Mesh 5, Mesh 2, Mesh 3, Mesh 4 그리고 Mesh 1 순서로 빠르게 산정되었다.

Fig. 9

Maximum Water Level (a) at field surveyed points and (b) at the gauges of physical model

Table 4

L₁ of Flood Arrival Time at the Electric Transformers and Gauges of Physical Model

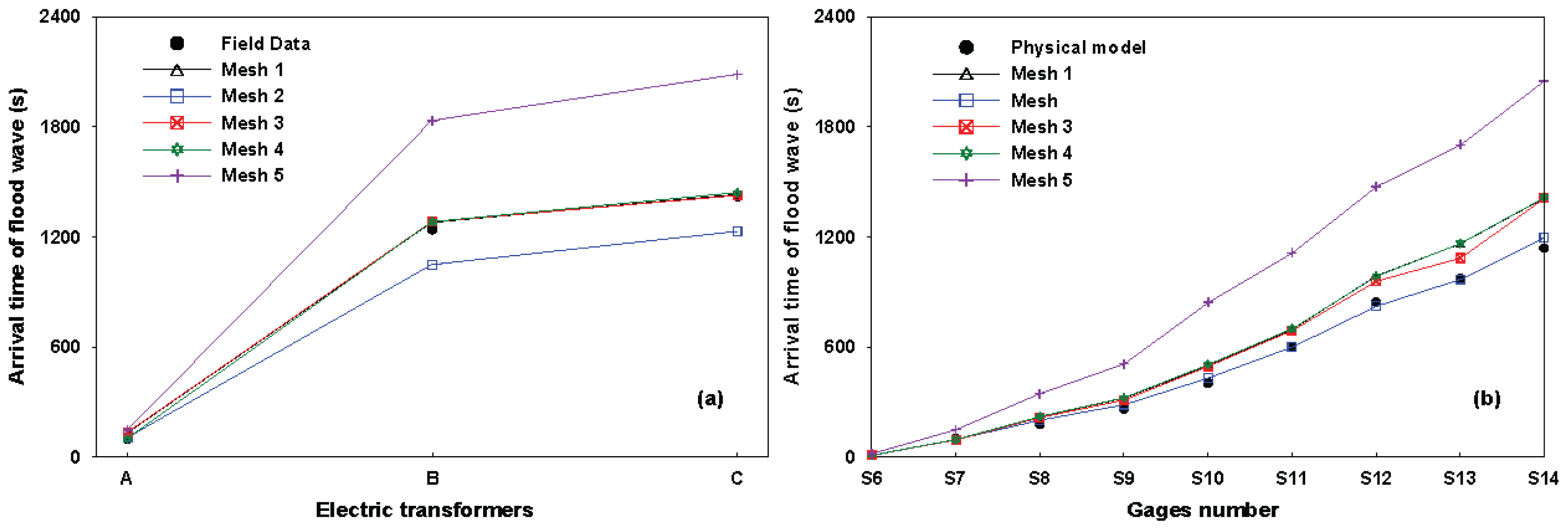
댐 붕괴 당시 하류부에는 3개의 전신주가 존재하고 있었으며, 댐 붕괴로 인한 이 전신주들의 정전시간은 알려져 있다. 3개 전신주의 위치는 Fig. 7에서 A, B, C로 나타내었다. Fig. 7에서 보여주듯이, 전신주 A는 댐 직하류부 계곡 부분에 위치해 있으므로 정전시간을 최초 홍수파 도달시간으로 고려하였고, 전신주 B, C는 댐과 상당한 거리에 위치해 있으므로 이 전신주들의 정전시간은 최초 홍수파 도달시간과 최고 홍수위 도달시간 사이로 간주하였다(Goutal et al., 1999). 위와 같이 고려하여 2차원 홍수모형에서 계산된 홍수파 도달시간과 전신주의 정전시간을 비교하여 Fig. 10(a)에 나타내었으며, 실험실 모형의 게이지(S6∼S14)에서 측정한 홍수파 도달시간과 계산된 도달시간과도 비교하여 Fig. 10(b)에 나타내었다. 또한, 전신주 정전시간 및 실험모형 도달시간과 수치모형에서 예측한 홍수파 도달시간과의 L₁오차를 산정하여 Table 4에 나타내었다. Fig. 10(a)과 Table 4에서 보여주듯이, Mesh 2에서 계산된 홍수파는 전신주 정전시간보다 빠르게 전파하고, Mesh 5에서는 정전시간보다 매우 늦게 전파한 반면, Mesh 1, Mesh 3, Mesh 4에서는 정전시간과 비교적 잘 일치한다. 하지만, 실험모형에서 측정한 홍수파 도달시간과 계산된 홍수파 도달시간과의 비교에서는 다른 결과를 보여준다. 실험모형에서는 Mesh 2에서 가장 정확한 홍수파 도달시간을 예측하였으며 Mesh 1, Mesh 3, Mesh 4에서는 실험모형의 전파시간과 비교해서 다소 느리게, Mesh 5에서는 매우 느리게 산정되었다(Fig. 10(b), Table 4).

Fig. 10

Flood Arrival Time (a) to the electronic transformers and (b) to the gauges of physical model

댐 붕괴 홍수파 전파시간에 대한 이해를 점 더 용이하도록 하기 위해서, 댐 붕괴 후 3600초 동안 각 격자에 대한 홍수파의 전파시간을 표현하여 Fig. 11에 나타내었다. Mesh 1, Mesh 3, Mesh 4에서의 홍수파 전파시간과 비교해서 Mesh 2에서의 홍수파는 더 빠르게 전파하며, Mesh 5에서는 매우 늦게 전파하고 있다. 홍수파 도달시간 비교에서(Fig. 11), Mesh 2에서의 결과는 동일 연구유역에 대해 조도계수를 변화시키면서 홍수파 도달시간의 정확도를 분석하는 연구를 수행한 Dewals et al. (2006)의 n=0.029 m^-1/3s(K=35 m^-1/3s)의 적용결과와 비슷하며, Mesh 1, Mesh 3 and Mesh 4에서의 결과는 n=0.05 m^-1/3s(K=20 m^-1/3s)의 적용결과와 비슷함을 보여준다. 이러한 결과의 원인으로 격자유형에 따른 하상 조도계수의 영향을 생각해 볼 수 있다. 즉, Mesh 2에서 사용된 사각격자가 Mesh 1, Mesh 3 and Mesh 4에서 사용된 삼각격자보다 지형을 더 부드럽게 표현함으로써 하상 조도의 영향을 더 작게 받아 홍수파 전파시간이 더 빠른 경향이 있다. 하지만, 정방형 격자가 사용된 Mesh 5는 계산영역에 대해 일정한 해상도(61.84 m)를 가진 다소 큰 격자를 생성함으로써 하천 지형을 정확하게 반영하지 못함으로 인해 (다른 격자들은 하천에 대해 격자를 조밀하게 생성) 홍수파 전파시간이 늦어졌다. Fig. 11에서 보듯이, 댐 붕괴로 인한 홍수파는 하천을 중심으로 전파하면서 범람하는 양상을 보여주며, 댐 하류의 폭이 좁고 경사가 급한 계곡에서는 빠르게 하류로 전파하지만, 홍수터가 넓어지는 하류로 내려올수록 홍수파의 전파는 느려지고 파의 선단은 넓은 지역에 걸쳐 퍼진다.

Fig. 11

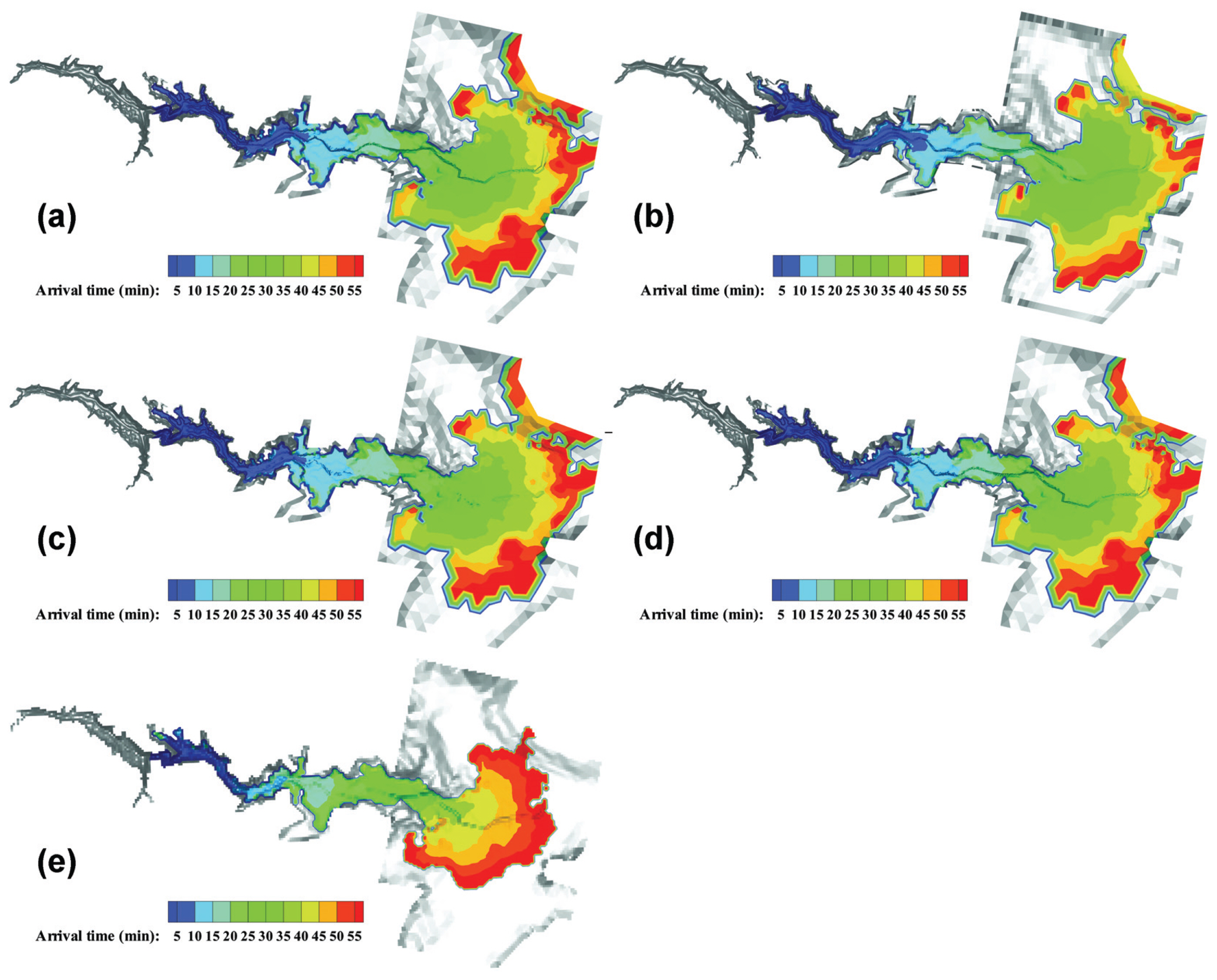
Contours of Flood Arrival Time; (a) Triangular mesh, (b) Quadrilateral mesh, (c) Mixed mesh with quadrilaterals along the river and triangles everywhere else, (d) Mixes triangles and quadrilaterals everywhere, and (e) Cartesian grid

위와 같은 연구결과는 실제 댐 붕괴가 발생한 지형에 대해 삼각, 사각 그리고 혼합격자에 적용한 VFRs 기법이 모형의 계산시간에는 큰 영향을 주지 않으면서, 동시에 높은 정확도롤 가지고 격자에서 발생하는 부분 마음/젖음 문제를 효율적으로 처리할 수 있음을 보여주었다. 또한, VFRs 기법을 적용한 모형의 정확도 및 계산기산은 일반적인 2차원 홍수해석모형과 마찬가지로 격자의 형상에 의해서 결정되기보다는 적용한 격자의 개수 및 정확한 지형의 반영도에 따라 결정될 수 있음을 보여주었다. 다만, 사각격자가 삼각격자보다는 지형을 더 부드럽게 표현함으로써 동일한 조도계수를 적용하더라도 그 반영도가 더 작음을 보여주었다.